ML - 5

회귀

회귀 vs 분류

지금까지 학습한 머신러닝 모델들은 여러 피처들을 사용하여 특정 라벨로 분류하는 알고리즘 이였는데 지금부터 해볼것은 회귀 문제이다.

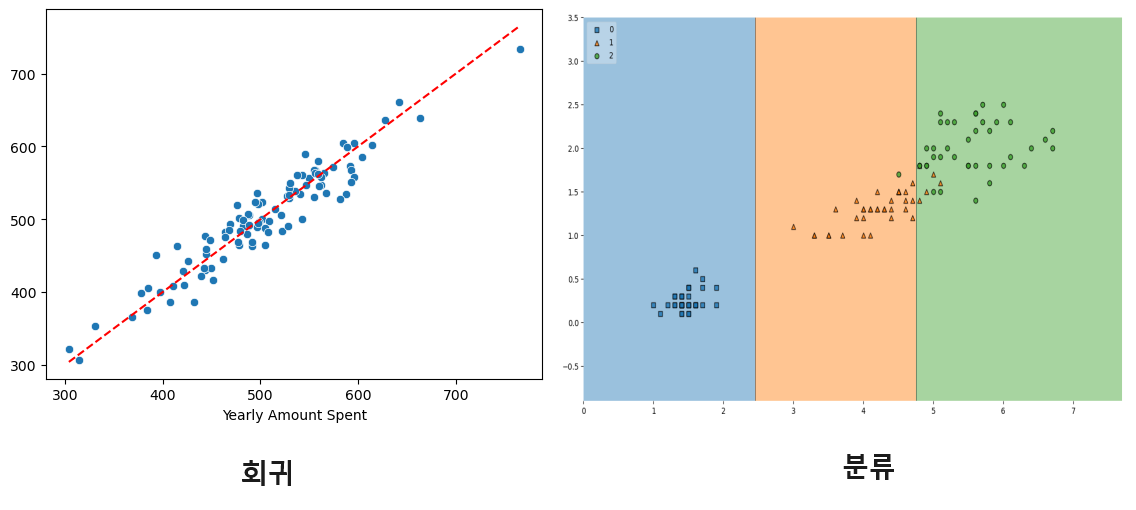
회귀: 출력 변수가 연속적인 값을 가집니다. 즉, 예측하려는 값이 숫자로 이루어져 있습니다. 예를 들면 주택 가격 예측, 온도 예측 등이 있습니다.

분류: 출력 변수가 이산적인 클래스 또는 범주를 나타냅니다. 모델은 입력을 특정 클래스로 할당하려고 시도합니다. 예를 들면 스팸 여부 판별, 손글씨 숫자 인식 등이 있습니다.

회귀: 모델의 출력은 연속적인 값입니다. 예를 들어, 300,000달러 또는 25도 Celsius와 같이 연속적인 범위의 수치입니다.

분류: 모델의 출력은 이산적인 클래스 레이블입니다. 예를 들어, "스팸" 또는 "정상 메일"과 같이 몇 개의 클래스 중 하나일 수 있습니다.

회귀: 주로 선형 회귀, 다항 회귀 등을 사용하여 입력 변수와 출력 변수 간의 관계를 모델링합니다.

분류: 로지스틱 회귀, 의사결정 트리, 신경망 등 다양한 알고리즘이 사용됩니다. 목표는 입력 변수를 여러 클래스 중 하나로 분류하는 것입니다.

회귀: 주로 평균 제곱 오차(Mean Squared Error, MSE)나 평균 절대 오차(Mean Absolute Error, MAE) 등을 사용하여 예측의 정확성을 측정합니다.

분류: 정확도(Accuracy), 정밀도(Precision), 재현율(Recall), F1 점수 등을 사용하여 모델의 분류 성능을 평가합니다.

간단히 말하면, 회귀는 연속적인 값을 예측하는 문제에 사용되고, 분류는 이산적인 클래스를 예측하는 문제에 사용됩니다.

선형 회귀

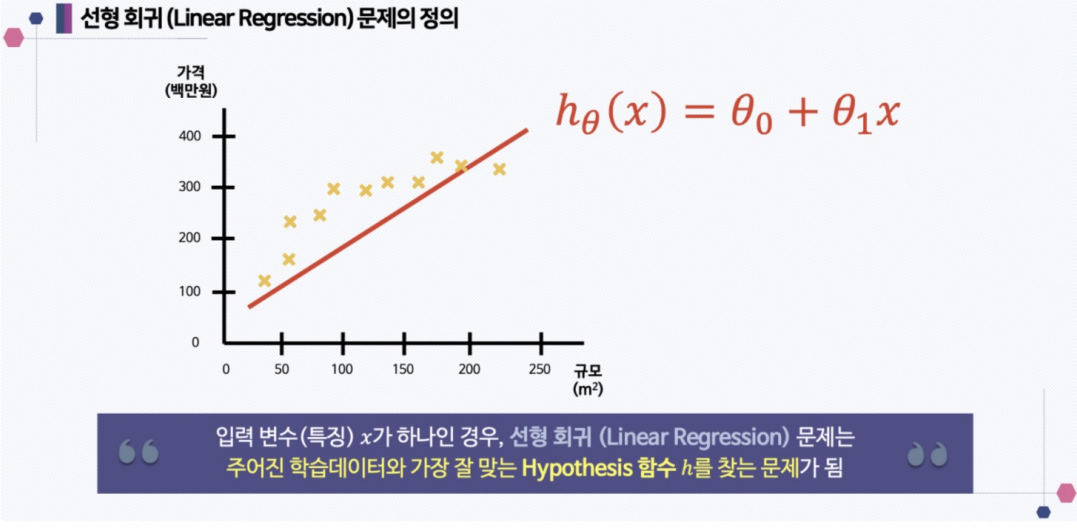
최소제곱법(Least Ordinary Sqaures)

최소제곱법(Least Squares)은 회귀 분석에서 사용되는 방법으로, 주어진 데이터와 모델 사이의 잔차(예측 오차)를 최소화하여 모델의 파라미터를 조정하는 것입니다. 이 방법은 데이터와 모델 예측 값 간의 제곱 오차를 최소화함으로써 최적의 모델 파라미터를 찾습니다. 최소제곱법은 계수들을 추정하고 예측을 개선하는데 효과적이며, 선형 회귀와 같은 모델에서 많이 사용됩니다.

아래와 같이 5개의 점을 주고 해당 점을 이용하여 희귀 모델을 만드는 방법은 다음과 같다.

import pandas as pd

# 다양한 통계 분석을 할 수 있는 라이브러리
import statsmodels.formula.api as smf

data = {'x': [1,2,3,4,5], 'y':[1,3,4,6,5]}
df = pd.DataFrame(data)
lm_model = smf.ols(formula='y ~ x', data=df).fit()

lm_model.params
Intercept 0.5
x 1.1
$y$ = 1.1$x$ + 0.5

파이썬 코드를 이용하여 위의 복잡한 행렬식을 해결할 수 있다.

sns.lmplot(x='x', y='y', data=df);
plt.xlim(0,5)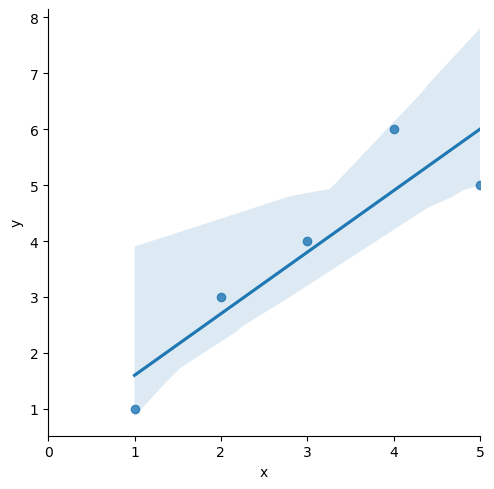

lmplot 예전에 배운 seaborn 그래프 중 하나로 column 간의 선형관계를 확인하기에 용이한 차트이다.

잔차 평가

잔차 평가는 회귀 모델의 예측 값과 실제 관측 값 간의 차이를 나타내는 잔차(residuals)를 분석하는 것입니다. 작은 잔차는 모델이 데이터를 잘 설명하고 있다는 것을 나타내며, 큰 잔차는 모델의 부적합을 나타낼 수 있습니다. 잔차 평가를 통해 모델의 성능을 평가하고 개선할 수 있습니다.

resid = lm_model.resid
resid

0 -0.6
1 0.3
2 0.2
3 1.1
4 -1.0

결정계수

결정 계수는 회귀 모델의 적합도를 나타내는 지표로, 모델이 종속 변수의 변동 중 얼마나 설명할 수 있는지를 나타냅니다. 보통 0에서 1 사이의 값으로 표현되며, 1에 가까울수록 모델이 데이터를 잘 설명하고 있다는 것을 의미합니다. 하지만 과적합의 가능성이 있으므로 주의가 필요합니다.

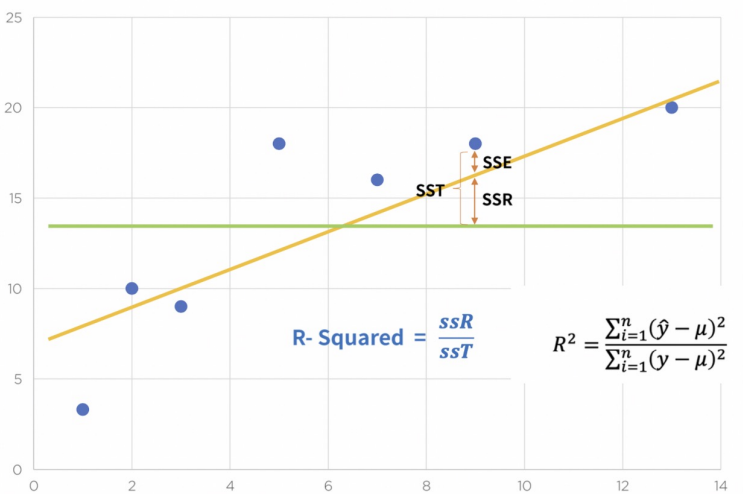
위의 식을 파이썬으로 작성하면 다음과 같다

mu = np.mean(df['y'])
y = df['y']

y_hat =  lm_model.predict()
np.sum((y_hat - mu)**2) / np.sum((y - mu)**2 )

> 0.8175675675675674

간단하게 출력할려면 다음과 같이 위에서 학습시킨 모델에 rsquared를 해주면된다.

lm_model.rsquared
> 0.8175675675675674

잔차의 분포표

sns.distplot(resid, color='black');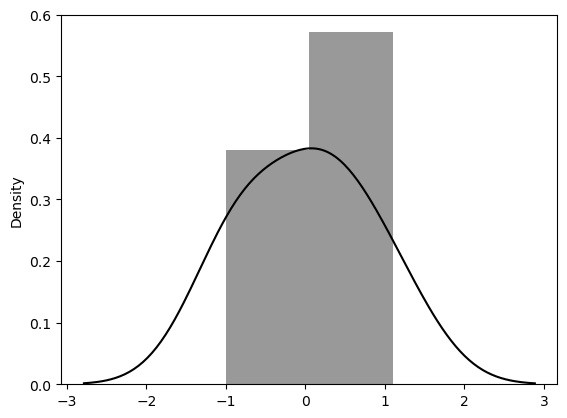

통계적 회귀

이커머스 회사 데이터 분석

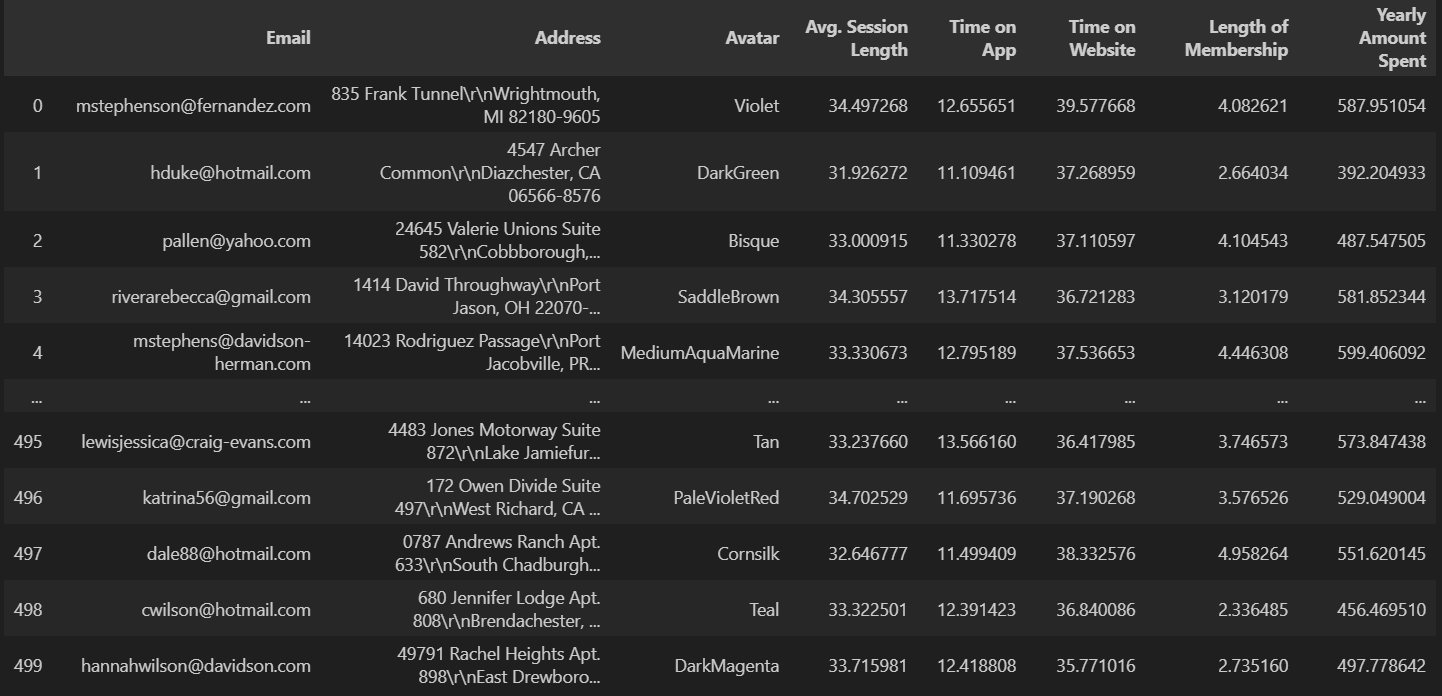
• Avg. Session Length : 한번 접속하였을 때 평균 어느 정도의 시간을 사용하는지에 대한 데이터
• Time on App : 폰 앱으로 접속했을 때 유지 시간 (분)
• Time on Website : 웹사이트로 접속했을 때 유지 시간(분)
• Length of Membership : 회원 자격 유지 기간 (연)

'Email', 'Address', 'Avatar'에 대한 데이터는 필요없으므로 제거해주고 시각화 해주도록하였습니다.

data.drop(['Email', 'Address', 'Avatar'], axis=1, inplace=True)
plt.figure(figsize=(12,6))
sns.boxplot(data=data)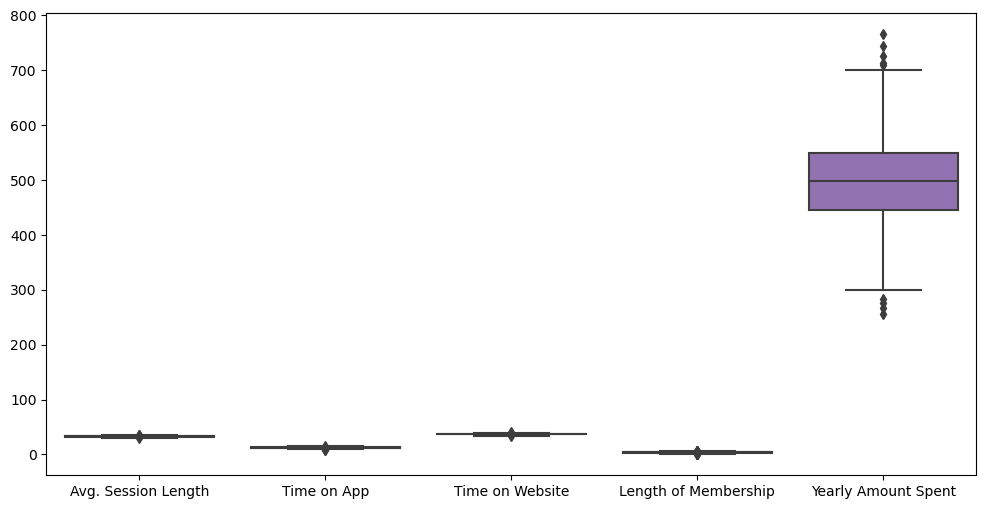

Yearly Amount Spent 값이 커서 참고가 안되니 Yearly Amount Spent값도 임시적으로 제외하고 다시 보면

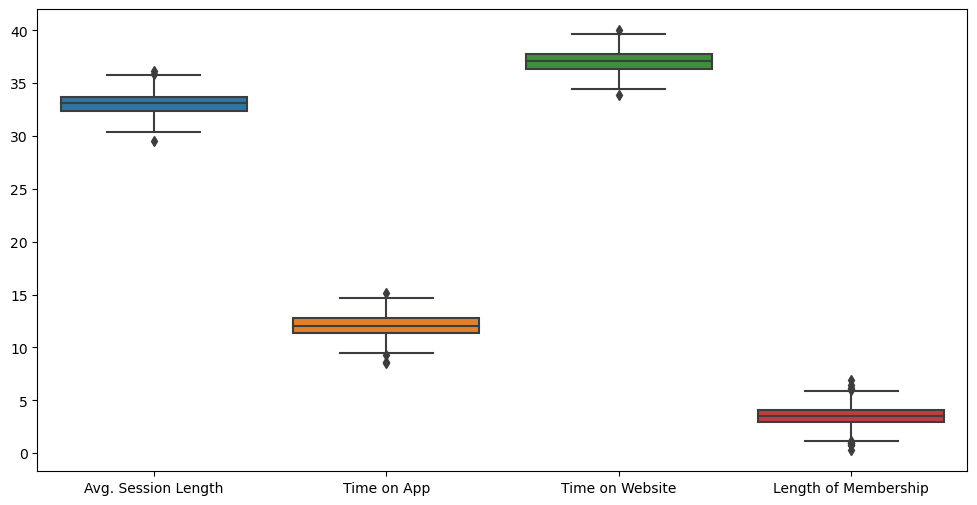
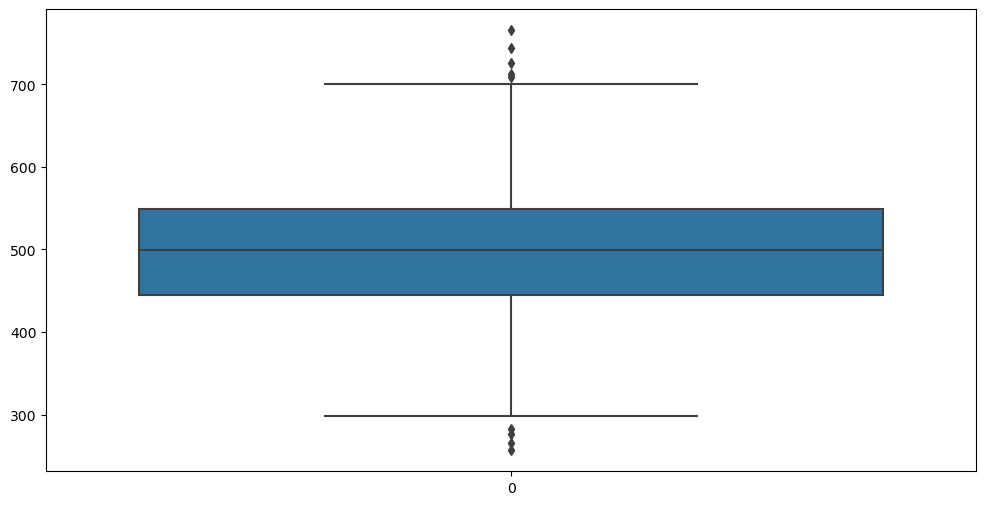
크게 이상치가 없어보이는 데이터임을 확인할수있다

이제 pairplot으로 데이터들의 상관 관계를 확인해보면

plt.figure(figsize=(12,6))
sns.pairplot(data=data)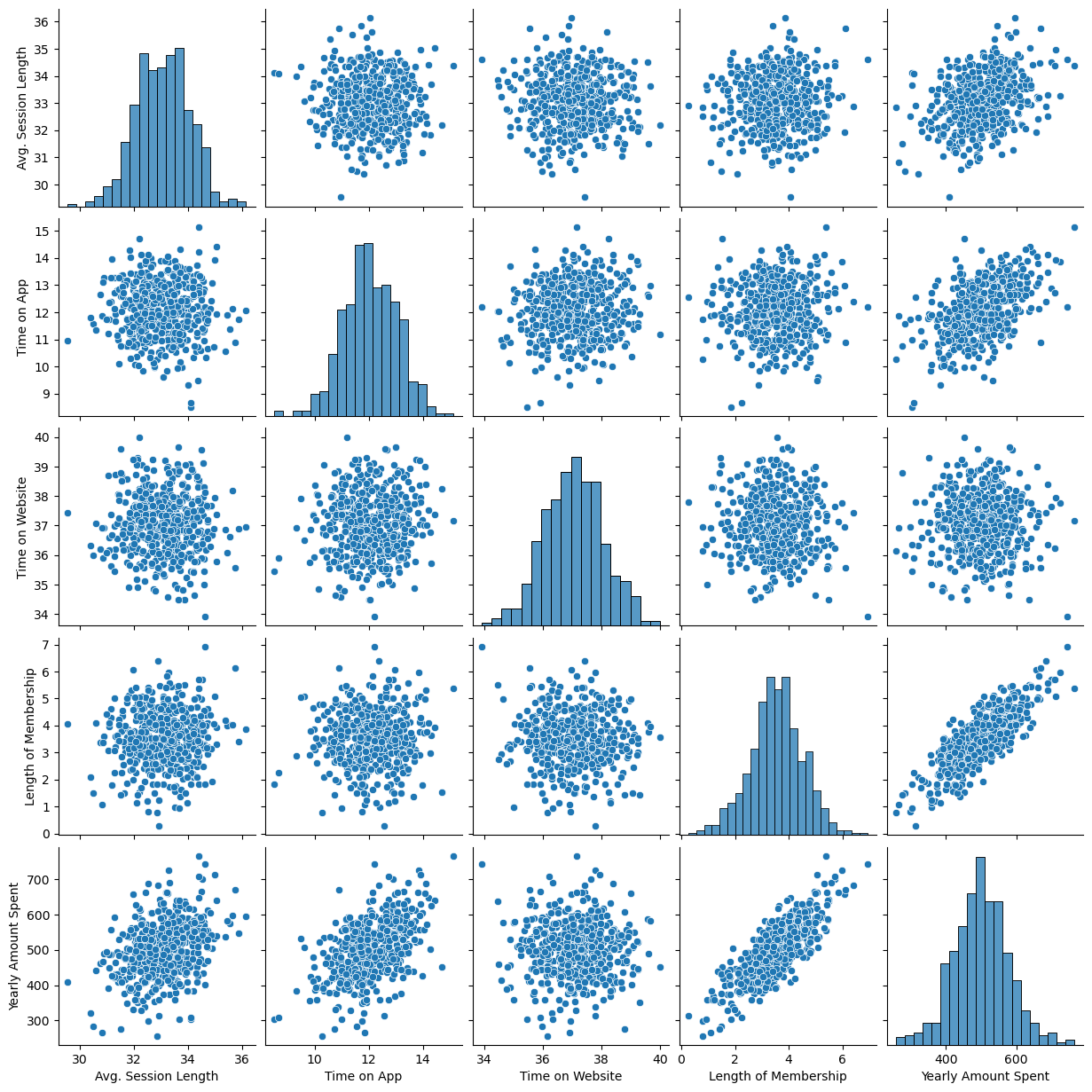

Length of Membership와 Yearly Amount Spent 데이터 사이에 상관관계가 있을 것으로 보인다.

plt.figure(figsize=(12,6))
sns.lmplot(x='Length of Membership', y='Yearly Amount Spent',data=data)

import statsmodels.api as sm

X = data['Length of Membership']
y = data['Yearly Amount Spent']

lm = sm.OLS(y, X).fit()

statsmodels.api 모델에 데이터를 학습시켜 모델 데이터의 요약해보면

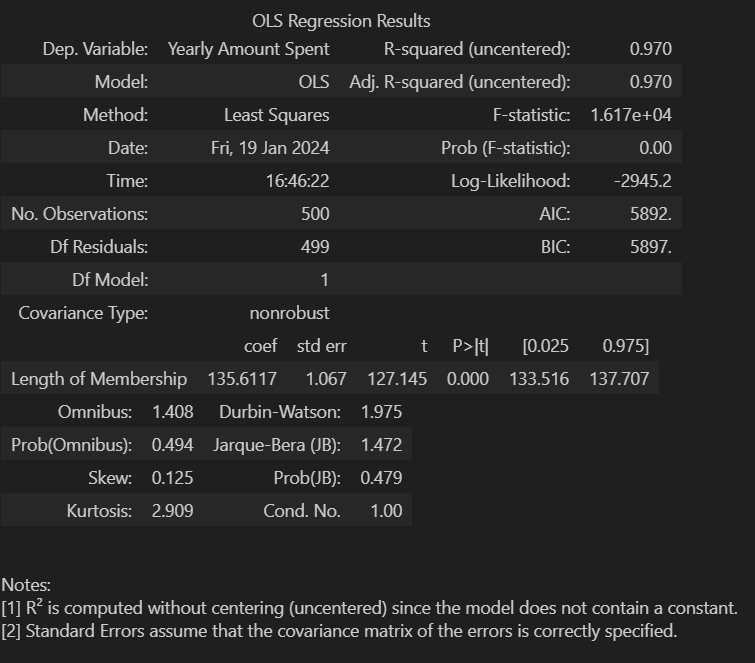
아래 오류사항을 읽어보면 $y$ = a$x$+b 에서 b값이 설정 되지 않았다는 메세지가 있는데 실제로 시각화 해보면 상수항이 0인걸 확인 할수있다.

pred = lm.predict(X)

sns.scatterplot(x=X, y=y)
plt.plot(X, pred, 'r', ls='dashed', lw=3)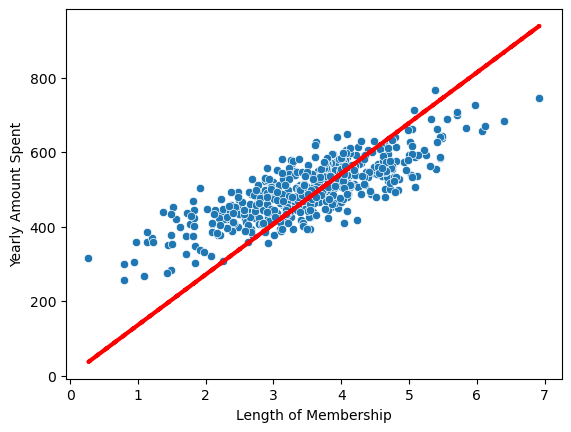

상수항을 numpy의 c_기능을 사용하여 추가 해주면

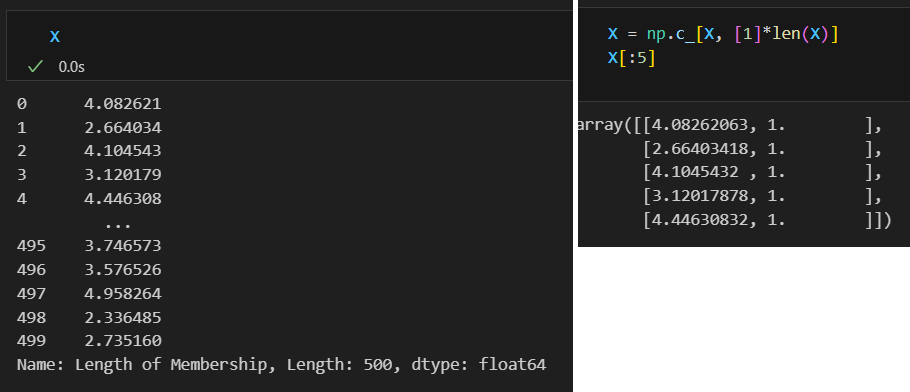
정보 재확인

lm = sm.OLS(y, X).fit()
lm.summary()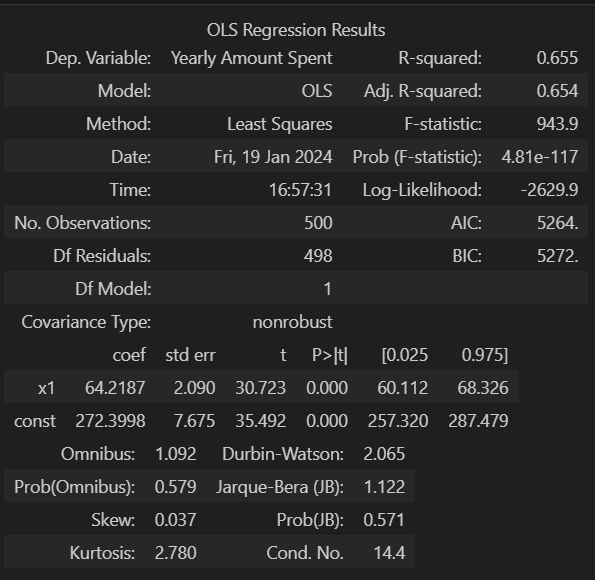

정확도는 낮아 졌지만 AIC와 BIC값이 내려가 더 좋은 모델이 되었음을 알수있다.

pred = lm.predict(X_test)

sns.scatterplot(x=y_test, y=pred)
plt.plot([min(y_test), max(y_test)], [min(y_test), max(y_test)], 'r', ls ='dashed')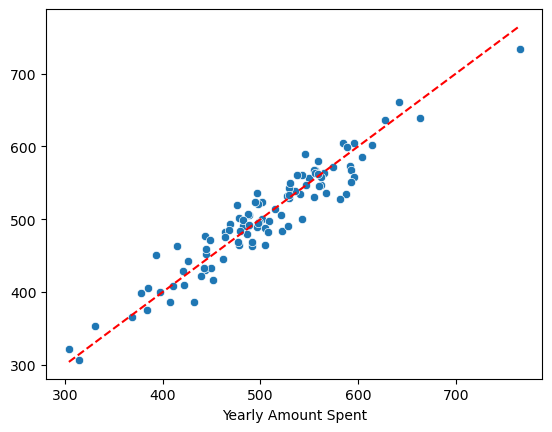

Cost_Function

Cost Function(비용 함수 또는 손실 함수)은 기계 학습에서 모델의 성능을 평가하고 모델을 최적화하는 데 사용되는 중요한 개념입니다. 이 함수는 모델의 예측이 실제 결과와 얼마나 차이나는지를 측정하여 모델을 향상시키는 방향으로 학습을 이끕니다.

간단히 말하면, Cost Function은 모델이 얼마나 '틀렸는지'를 나타내는 지표입니다. 모델이 훈련 데이터에 대해 얼마나 정확한지를 측정하여 모델이 최적화되도록 도와줍니다.

여기서 예를 들어보겠습니다. 선형 회귀(Linear Regression)에서, 모델은 주어진 데이터에 가장 잘 맞는 직선을 찾아야 합니다. Cost Function은 이 직선의 예측값과 실제 데이터 포인트 간의 거리를 측정합니다. 이 거리가 작을수록 모델의 성능이 좋다고 할 수 있습니다.

일반적으로 Cost Function은 다음과 같은 수식으로 표현됩니다:

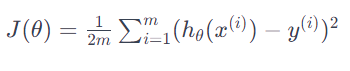
poly1d

poly1d는 numpy의 기능으로 n차 방정식을 생성해준다.

import numpy as np
# x + 1
a = np.poly1d([1,1])
# x - 1
b = np.poly1d([1, -1])

a * b
$x^2$ - 1

실습

(2,1), (3,5), (5,6)의 cost_function 구하기

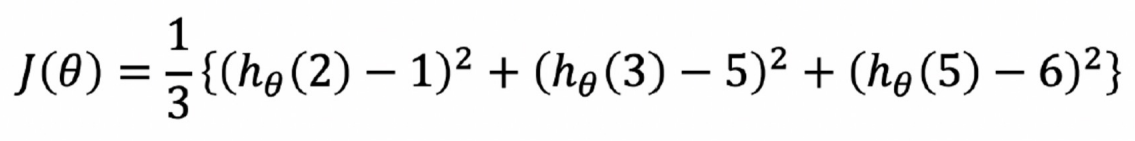
np.poly1d([2, -1]) ** 2 + np.poly1d([3, -5])**2 + np.poly1d([5, -6])**2

poly1d([ 38, -94, 62])
$y$ = 38$x^2$ - 94$x$ + 62

다음과 같은 함수를 얻을수 있었고

sympy를 통해 계산해보면

theta = sym.Symbol('theta')
diff_th = sym.diff(38*theta**2 -94*theta + 62, theta)
diff_th

76θ−94
$θ$ = 94/76

θ값을 구할수 있게 됩니다.

boston 집값 예측해보기

sklearn에서 기본예제로 제공해 주었으나 현재는 사라져 csv파일로 진행하였습니다.

import pandas as pd
boston = pd.read_csv('boston.csv')

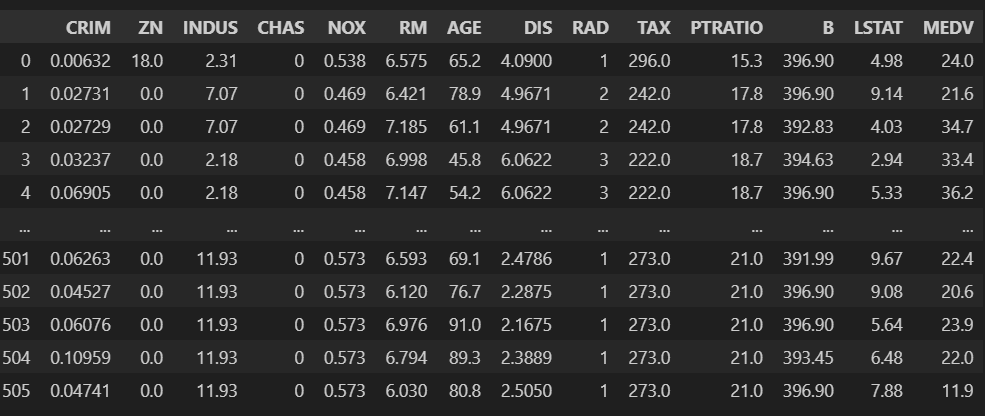
상관계수를 확인해 보면

corr_mat = boston.corr().round(1)
corr_mat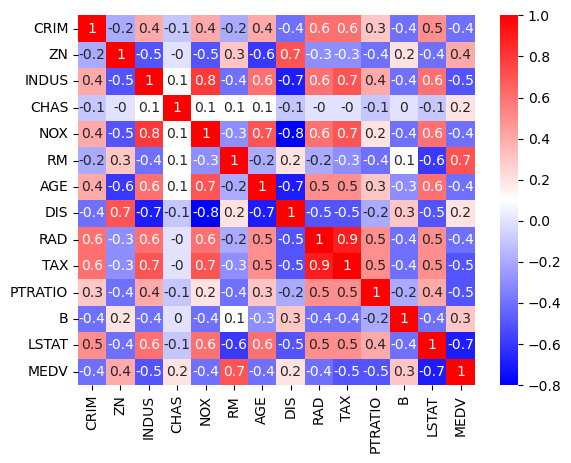

가격과 방의 개수 / 가격과 저소득층가 상관 관계가 그나마 있는것을 확인 할수있습니다.

sns.set_style('darkgrid')
sns.set(rc={'figure.figsize':(12,6)})

fig, ax = plt.subplots(ncols=2)
sns.regplot(x='RM', y='MEDV', data=boston, ax=ax[0])
sns.regplot(x='LSTAT', y='MEDV', data=boston, ax=ax[1])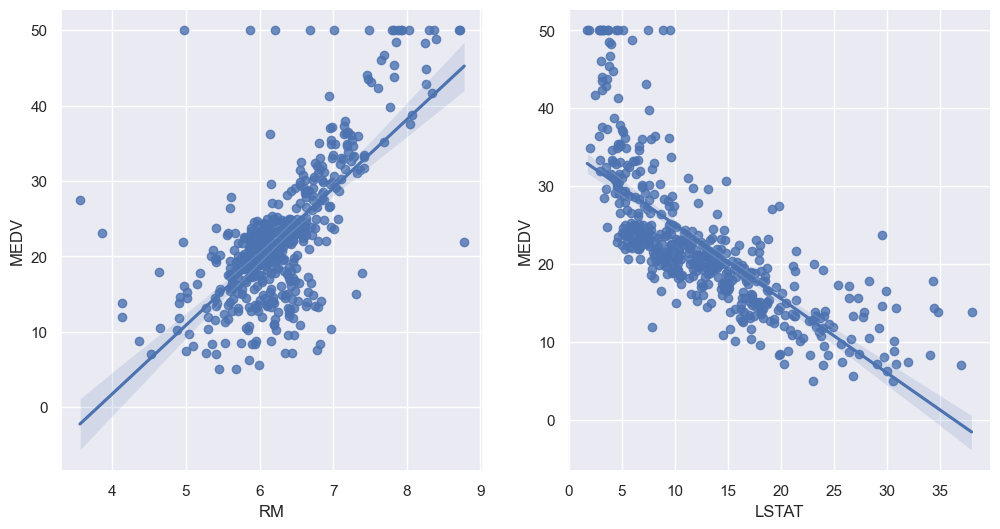

확실히 뭔가 관련성이 있어보이는데 선형회귀 모델에 학습 시켜보겠습니다.

방 계수와 가격

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
import numpy as np
from sklearn.metrics import mean_squared_error

X = boston.drop(['MEDV'], axis=1)
y = boston['MEDV']

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=13)

reg = LinearRegression()
reg.fit(X_train, y_train)

pred_tr = reg.predict(X_train)
pred_test = reg.predict(X_test)

mean_squared_error
mean_squared_error는 회귀 모델의 성능을 측정하는 지표 중 하나로, 모델이 예측한 값과 실제 값 간의 평균 제곱 오차를 계산합니다. 예측 오차를 제곱하여 평균을 구하므로 오차의 크기를 고려하며, 작은 값일수록 모델의 예측이 정확하다고 판단됩니다.

rmse_tr = (np.sqrt(mean_squared_error(y_train, pred_tr)))
rmse_test = (np.sqrt(mean_squared_error(y_test, pred_test)))

print('RMSE of Train data : ', rmse_tr)
print('RMSE of Test data : ', rmse_test)

RMSE of Train data : 4.642806069019824
RMSE of Test data : 4.931352584146716

모델 평가는 RMS로 하였습니다.

RMS는 "Root Mean Square"의 약어로, 평균 제곱근을 나타냅니다. RMS 평가는 주로 평균 제곱 오차(Mean Squared Error, MSE)에 제곱근을 취한 값으로, 모델의 예측과 실제 값 간의 평균적인 오차의 크기를 나타냅니다. 따라서 모델이 훈련 데이터에 대해 평균 제곱 오차를 계산한 후 이를 제곱근으로 변환하여 RMS 평가를 얻는 것을 나타냅니다. 이 값이 작을수록 모델의 성능이 향상되었다고 해석할 수 있습니다.

이제 예측한 모델과 실제 값이 얼마나 차이나는지 시각화 해보면

plt.scatter(y_test, pred_test)
plt.xlabel('Actual House Price ($1000)')
plt.ylabel('Predicted Price')
plt.title('REAL VS Predict')
plt.plot([0,48], [0,48], 'r')
plt.show()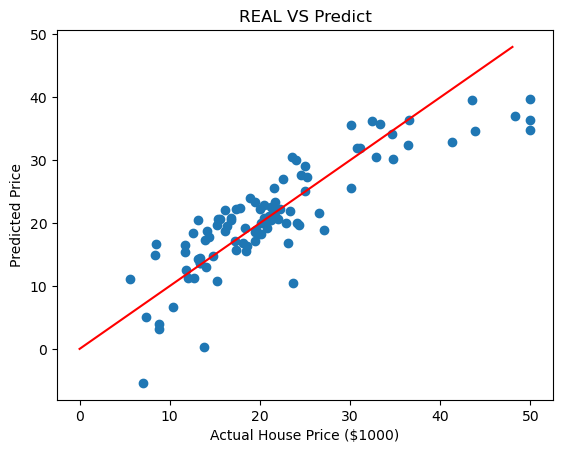

빈곤층 비율과 가격

X = boston.drop(['MEDV','LSTAT'], axis=1)
y = boston['MEDV']

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=13)

reg = LinearRegression()
reg.fit(X_train, y_train)

pred_tr = reg.predict(X_train)
pred_test = reg.predict(X_test)
rmse_tr = (np.sqrt(mean_squared_error(y_train, pred_tr)))
rmse_test = (np.sqrt(mean_squared_error(y_test, pred_test)))

print('RMSE of Train data : ', rmse_tr)
print('RMSE of Test data : ', rmse_test)

RMSE of Train data : 5.165137874244864
RMSE of Test data : 5.2955950325971655

마찬가지로 예측한 모델과 실제 값이 얼마나 차이나는지 시각화 해보면

plt.scatter(y_test, pred_test)
plt.xlabel('Actual House Price ($1000)')
plt.ylabel('Predicted Price')
plt.title('REAL VS Predict')
plt.plot([0,48], [0,48], 'r')
plt.show()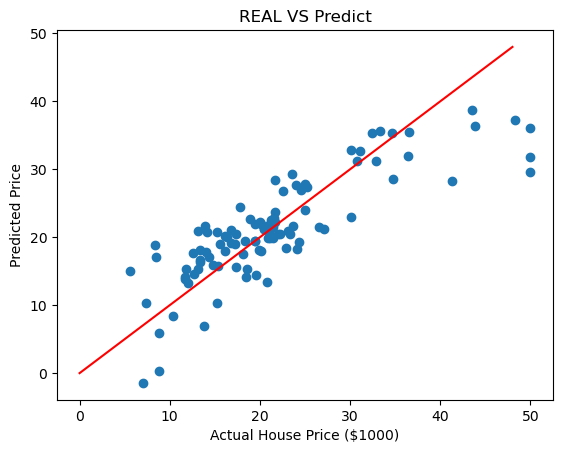

전체코드

선형회귀
통계적 회귀
Cost_Function

사진 출처 제로베이스