데이터 스쿨 3주차 학습내용 정리 - 1

제로베이스 데이터 스쿨 3주차 학습 내용 정리

이번 주차는 쉬어가는 느낌으로(?) 기초 수학 문제를 파이썬으로 구현하는 방법을 학습하였습니다.

01_약수와 소수

약수

약수는 어떤 정수를 나누어서 나머지가 0이 되는 정수입니다.
예를 들어, 10의 약수는 1, 2, 5, 10입니다.

파이썬 코드

num = int(input('0보다 큰 정수 입력 : '))
divisor = []
for number in range(1,(num + 1)):
    if num % number == 0:
        divisor.append(number)
print(divisor)

소수

소수는 1과 자기 자신만을 약수로 가지는 정수입니다.
예를 들어, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, ... 은 소수입니다.

파이썬 코드

num = int(input('0보다 큰 정수 입력 : '))
prime = []
for number in range(2, (num + 1)):
    flag = True
    for i in range(2, number):
        if number % i == 0:
            flag = False
            break
    if flag:
        prime.append(number)
print(prime)

02_소인수와 소인수분해

소인수

어떤 정수를 소수로만 나누어서 얻을 수 있는 약수를 소인수라고 합니다.
예를 들어, 10의 소인수는 2와 5입니다.

소인수분해

어떤 정수를 소인수로 분해하는 것을 소인수분해라고 합니다.
예를 들어, 10의 소인수분해는 2 * 5입니다.

파이썬 코드

num = int(input('1보다 큰 숫자를 입력해주세요 : '))
searchNumber = []
n = 2
while n <= num:
    if num % n == 0:
        print('소인수 : {}'.format(n))
        if searchNumber.count(n) == 0:
            searchNumber.append(n)
        elif searchNumber.count(n) == 1:
            searchNumber.remove(n)

        num /= n

    else:
        n += 1
print(searchNumber)

03_최대공약수

두 정수의 공통된 약수 중에서 가장 큰 약수를 최대공약수라고 합니다.
예를 들어, 10과 12의 최대공약수는 2입니다.

파이썬 코드

num1 = int(input('첫번째 숫자 : '))
num2 = int(input('두번째 숫자 : '))
num3 = int(input('세번째 숫자 : '))

number = []
maxNum = 0
for i in range(1, (num1+1)):
    if num1 % i == 0 and num2 % i == 0 and num3 % i == 0:
        print('공약수 : {}'.format(i))
        number.append(i)
        maxNum = i

print(number)
print('최대공약수 : {}'.format(maxNum))

이것이 일반 적인 최대 공약수를 구하는 방법이지만 유클리드 호재법이라는 방식으로도 구해 보았습니다.

유클리드 호재법

num1 = int(input('첫번째 숫자 : '))
num2 = int(input('두번째 숫자 : '))

temp1 = num1
temp2 = num2

number = []

while temp2 > 0:
    temp = temp2
    temp2 = temp1 % temp2
    temp1 = temp

print(temp1)
for i in range(1, temp1 + 1):
    if temp1 % i == 0:
        number.append(i)

print(number)

2개의 정수 한정이지만 이게 더 코드가 간결하여 저는 이 방법을 선호 하고 있습니다.

04_최소공배수

두 정수의 공통된 배수 중에서 가장 작은 배수를 최소공배수라고 합니다.
예를 들어, 10과 12의 최소공배수는 30입니다.

파이썬 코드

num1 = int(input('첫번째 숫자 : '))
num2 = int(input('두번째 숫자 : '))
num3 = int(input('세번째 숫자 : '))

number = []
maxNum = 0
maxNum2 = 0
for i in range(1, (num1+1)):
    if num1 % i == 0 and num2 % i == 0:
        print('공약수 : {}'.format(i))
        maxNum = i

minNum = num1 * num2 // maxNum
maxNum = minNum
for i in range(1, (maxNum + 1)):
    if minNum % i == 0 and num3 % i == 0:
        print('공약수 : {}'.format(i))
        number.append(i)
        maxNum2 = i
print('최대공약수 : {}'.format(maxNum2))

print('세 숫자의 최소 공배수 {}'.format(minNum * num3 / maxNum2))

print(number)

최대 공약수와 최소 공배수는 한 쌍이라고 봐도 무방한것이 우리가 일반적으로 최대 공약수와 최소 공배수를 구할 때를 생각해보면

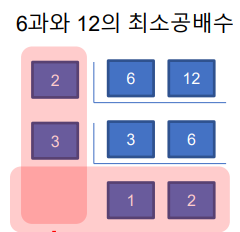
다음 그림과 같이 구하는데 최소 공배수는 두 수의 곱 / 최대 공약수 이므로 위에서 사용한 유클리드 호재법을 사용하면 더욱더 간단하게 구할수도 있습니다.

유클리드 호재법

num1 = int(input('첫번째 숫자 : '))
num2 = int(input('두번째 숫자 : '))

temp1 = num1
temp2 = num2

while temp2 > 0:
    temp = temp2
    temp2 = temp1 % temp2
    temp1 = temp

print('최대 공약수 : {}'.format(temp1))
print('최소 공배수 : {}'.format(num1 * num2 / temp1))

05_진법

진법이란
숫자를 표현하는 방법을 의미합니다. 진법은 숫자의 기수에 따라 2진법, 8진법, 10진법, 16진법 등으로 나뉩니다.

2진법
2진법은 숫자를 0과 1로만 표현하는 방법입니다. 2진법은 컴퓨터에서 숫자를 표현하는 데 사용됩니다.

8진법
8진법은 숫자를 0부터 7까지의 숫자로 표현하는 방법입니다. 8진법은 컴퓨터에서 메모리를 표현하는 데 사용됩니다.

10진법
10진법은 우리가 일상적으로 사용하는 숫자 표현 방법입니다. 10진법은 0부터 9까지의 숫자로 표현합니다.

16진법
16진법은 숫자를 0부터 9까지의 숫자와 A부터 F까지의 알파벳으로 표현하는 방법입니다. 16진법은 컴퓨터에서 색상을 표현하는 데 사용됩니다.

파이썬 코드

num = int(input('숫자를 입력하세요'))

print(hex(num))
print(bin(num))
print(oct(num))

print('2진수(0b11110) -> 8진수({})'.format(oct(0b11110)))
print('2진수(0b11110) -> 10진수({})'.format(int(0b11110)))
print('2진수(0b11110) -> 16진수({})'.format(hex(0b11110)))

print('8진수(0o36) -> 2진수({})'.format(bin(0o36)))
print('8진수(0o36) -> 10진수({})'.format(int(0o36)))
print('8진수(0o36) -> 16진수({})'.format(hex(0o36)))

print('16진수(0x1e) -> 2진수({})'.format(bin(0x1e)))
print('16진수(0x1e) -> 8진수({})'.format(int(0x1e)))
print('16진수(0x1e) -> 10진수({})'.format(hex(0x1e)))