제로베이스 데이터 스쿨 3주차 학습 내용 정리 - 3
이번 주차는 쉬어가는 느낌으로(?) 기초 수학 문제를 파이썬으로 구현하는 방법을 학습하였습니다.
10_팩토리얼
팩토리얼은 1부터 n까지의 정수를 차례로 곱한 값을 의미합니다.
팩토리얼의 기호는 n!로 표기합니다.
예를 들어, 5!는 1부터 5까지의 정수를 차례로 곱한 값으로, 120입니다.
5! = 1 x 2 x 3 x 4 x 5 = 120
팩토리얼은 순열, 조합, 확률 등 다양한 분야에서 사용됩니다.
파이썬으로 펙토리얼을 구하는 방법을 3가지를 다뤗는데 하나씩 소개하도록 하겠습니다.
python 코드
# def facFun1(n):
# fac = 1
# for i in range(1, n+1):
# fac *= i
# return fac위의 코드가 가장 일반적인 방법이라고 생각합니다.(쓸일은 없을꺼 같지만)
함수로 선언하여 1부터 n까지의 값을 곱해 return해주는 함수입니다.
# def facFun2(n):
# if n == 1:
# return n
#
# return n * facFun2(n-1)
import math
print(math.factorial(num))이번 코드는 재귀 함수 형식의 방법인데 특정 조건을 만족할때까지 함수 내부를 반복 실행하는 함수입니다. 이 경우 n을 1씩 깎으며 1이 되는 순간 빠져나오는 식으로 설계 되어있습니다.
num = int(input('input Number : '))
# print(f'{num}! : {facFun1(num)}')이 방법을 마지막으로 소개한 이유는 보자마자 아시겠지만 파이썬 내부모듈인 math를 사용하면 한번에 펙토리얼 값을 얻어 낼 수 있습니다.
11_군수열
군수열은 n개의 서로 다른 정수로 이루어진 수열입니다.

말로는 설명이 힘들어 제로베이스 강의자료를 가져왔습니다. ㅎㅎ
예를 들어, (1), (1, 2), (1, 2, 3), (1, 2, 3, 4), ...는 군수열입니다.
python 코드
inputN = int(input('n항 입력 : '))
flag = True
n = 1; cntN = 1; searchN = 0
while flag:
for i in range(1, (n + 1)):
if i == n:
print('{}'.format(i), end=' ')
else:
print('{}'.format(i), end=',')
cntN += 1
if cntN > inputN:
searchN = i
flag = False
break
print()
n += 1
print('{}항 : {}'.format(inputN, searchN))코드의 첫 줄에서 사용자로부터 n항을 입력받습니다.
n, cntN, searchN이라는 변수를 선언합니다. n은 현재 항의 번호를 나타내는 변수, cntN은 출력된 항의 개수를 나타내는 변수, searchN은 n항의 값을 저장하기 위한 변수입니다.
다음 줄에서 while문을 시작합니다. while문은 flag가 True일 때까지 반복합니다.
while문 안에서 for문을 사용하여 1부터 n까지의 자연수를 출력합니다.
for문이 종료되면 cntN을 1 증가시킵니다. 그리고 cntN이 입력받은 n보다 크거나 같으면 flag를 False로 설정하고, while문을 종료합니다.
12_순열
순열은 n개의 서로 다른 정수를 일정한 순서로 나열한 것입니다.
순열의 기본 형식은 다음과 같습니다.
nPr
P는 순열을 의미합니다. n은 순열에 포함되는 정수의 개수를 의미합니다. r은 순열의 길이를 의미합니다.
예를 들어, 1, 2, 3, 4의 순열은 다음과 같이 표기할 수 있습니다.
4P3 = 12
(1,2,3) ,(1,2,4) ,(1,3,4) ,(1,3,2), (1,3,4) ,(1,4,3)...
총 12가지 경우의 수를 나타냅니다.
이를 구하는 공식으로

위 그림과 같은 공식이 존재하는데 이를 파이썬에서 n, r 값을 input()으로 받아서 푸는 방식으로 진행하였습니다.
python 코드
numN = int(input('n값 입력 : '))
numR = int(input('r값 입력 : '))
result = 1
for i in range(numN, (numN - numR), -1):
result = result * i
print('{}P{} = {}'.format(numN, numR, result))해설을 듣기전에 혼자 고민해 보았으나 range안에 range(numN, (numN - numR), -1)를 넣는 발상을 한사람은 대단한거 같다...3줄정도 휘갈기고 있었는데 1줄이라니....
13_조합
조합은 n개의 서로 다른 정수 중에서 r개의 정수를 일정한 순서 없이 선택한 것입니다.
조합의 기본 형식은 다음과 같습니다.
nCr
C는 조합을 의미합니다. n은 조합에 포함되는 정수의 개수를 의미합니다. r은 조합의 크기를 의미합니다.
4C2 = 6
(1,2), (1,3), (1,4), (2,3), (2,4), (3,4)
이 처럼 순서가 없기 때문에 (1,2)와 (2,1)은 같은 칩니다.
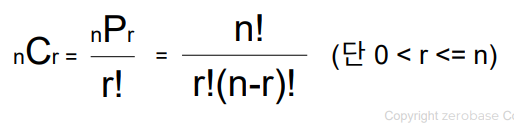
마찬가지로 다음과 같은 공식을 파이썬으로 구현하여 구해줍니다.
python 코드
numN = int(input('n값 입력 : '))
numR = int(input('r값 입력 : '))
resultP = 1
resultR = 1
resultC = 1
for i in range(numN, numN - numR, -1):
print('n : {}'.format(i))
resultP *= i
for i in range(1, numR + 1):
print('n : {}'.format(i))
resultR *= i
resultC = resultP / resultR
print('{}P{} : {}'.format(numN, numR, int(resultP)))
print('{}C{} : {}'.format(numN, numR, int(resultC)))공식을 보면 알겠지만 순열 나누기 r!이기때문에 순열 코드에 r!값을 따로구한 다음 나눠주기만 한것이다
펙토리얼 > 순열 > 조합 순으로 코드를 짜는건 이것을 위한 빌드업
14_확률
확률은 어떤 사건이 일어날 가능성을 나타내는 수입니다.
확률의 기본 공식은 다음과 같습니다.
P(A) = n(A) / n(S)
P(A)는 사건 A가 일어날 확률을 의미합니다. n(A)는 사건 A가 일어날 경우의 수를 의미합니다. n(S)는 전체 경우의 수를 의미합니다.
예를 들어, 동전 한 면을 던질 때 앞면이 나올 확률은 다음과 같이 계산할 수 있습니다.
P(앞면) = n(앞면) / n(전체)
n(앞면)은 앞면이 나올 경우의 수는 1입니다. n(전체)는 전체 경우의 수는 2입니다. 따라서 앞면이 나올 확률은 1/2입니다.
python 코드
이것은 문제 따라서 코드가 변함으로 문제를 첨부 하겠습니다.

# numN = int(input('n값 입력 : '))
# numR = int(input('r값 입력 : '))
resultC = 1
resultP = 1
resultR = 1
def com(n, r):
resultP = 1
resultR = 1
for i in range(n, n - r, -1):
resultP *= i
for i in range(1, r+1):
resultR *= i
resultC = resultP / resultR
return int(resultC)
print(round((com(4,2) * com(3,1)) / com(7,3)*100,2))위에서 구한 조합의 코드를 def로 함수처리 하여 경우의 수를 구하여 100을 곱해주면 끝!

