Recursive, Tree, Graph(DFS, BFS)

7-1

class Main{
	public void DFS(int n){
    	if (n==0) return;
        else {
        	DFS(n-1);	// 5번 라인
            System.out.print(n + " ");
        }
    }
}

위와 같은 형태의 재귀함수는 Stack프레임에 쌓이게 된다.

D(0)
D(1) - Line5
D(2) - Line5
D(3) - Line5

D(3)부터 차근차근 쌓인 뒤 D(0)부터 다시 빠져나간다. 따라서 이를 Stack 형태라고 할 수 있다.

7-2

class Main{
	public void DFS(int n){
    	if (n==0) return;
        else {
        	DFS(n / 2);	// 5번 라인
            System.out.print(n % 2 + " ");
        }
    }
}

D(0)
D(1) - Line5
D(2) - Line5
D(5) - Line5
D(11) - Line5

7-4

피보나치 수열

public int DFS(int n) {
	if (n==1) return 1;
    else if (n==2) return 1;
    else return DFS(n-2) + DFS(n-1);
}

위의 방법은 일반적인 재귀 호출 방식으로 만든 것이다. 이 때 main문 안에서는 피보나치 수열을 구할 때 여러개를 호출해야 한다면 각각의 값을 다 따로 구해주어야 할 것이다.

static int[] fibo;
public int DFS(int n) {
	if (n==1) return fibo[n] = 1;
    else if (n==2) return fibo[n] = 1;
    else return fibo[n] = DFS(n-2) + DFS(n-1);
}

위와 같이 fibo라는 배열을 미리 선언해 놓고 DFS(n)만 한번 돌린다면 fibo라는 배열 속에 모든 피보나치 수열의 정보가 들어가게 된다. 속도가 위의 것 보다 대략 1.5배정도 빨라지는 것을 확인 했다.
하지만 이렇게 만들었을 때 DFS(45)가 실행되면 DFS(43)과 DFS(44)가 전부 다시 실행되는 것은 똑같다. 이를 해결하기 위한 방법이 있다.

~~
if(fibo[n]>0) return fibo[n];
~~

위의 것을 가장 위에 써준다. 예를 들어 DFS(45)를 실행한다고 해보자. DFS(43)+DFS(44)의 계산이 있을텐데, DFS(43)을 계산하면 fibo의 배열 안에 fibo[43]까지의 값이 모두 채워져 있을 것이다. 따라서 DFS(44)를 계산할 때에 다시 전부 계산할 필요가 없어진다. 이렇게 할 시에 연산 속도는 매우 빨라진다.

7-5

이진트리 순회

class Node{
	int data;
    Node lt;
    Node rt;
    
    Node(int data){
    	this.data = data;
        lt = rt = null;
	}
}

위와 같이 이진 트리의 형태를 만들어준다. root와 왼쪽 오른쪽인 lt, rt 존재

Node root;
public void DFS(Node root){
	if (root == null) return;
    else {
        //System.out.print(root.data + " "); -> 전위순회
        DFS(root.lt);
        //System.out.print(root.data + " "); -> 중위순회        
        DFS(root.rt);
        //System.out.print(root.data + " "); -> 후위순회
	}
}

위에서 print의 위치를 어디에 두느냐에 따라 순회 방식이 달라진다. 이는 1,2번과 같이 stack형태로 써보면 쉽게 알 수 있다.

7-7

이진트리 레벨탐색 (BFS)

우선 위의 Node class는 그대로 받아온다.

Node root;
public void BFS(Node root) {
	Queue<Node> Q = new LinkedList<>();
    Q.offer(root);
    int L=0;
    while (!Q.isEmpty()) {
    	int len = Q.size();
        System.out.print(L+" : ");
        for (int i=0; i<len; i++) {
        	Node current = Q.poll();
            System.out.print(current.data + " ");
            if(current.lt!=null) Q.offer(current.lt);
            if(current.rt!=null) Q.offer(current.rt);
        }
        L++
        sout
    }
}

위에서와 같이 Queue를 만들어준다. 이것은 위의 DFS와 다르게 Stack이 아닌 Queue의 형태로 쓰이는데, 먼저 들어온 것이 먼저 나가게 된다.
Q에 root값을 넣고, 그것을 출력한 뒤 lt와 rt의 값을 Q로 다시 끌고온다. 이를 반복하다 보면 level별로 탐색할 수 있게 된다.

7-8

위에서 했던 BFS의 방식을 그대로 받아온다.
5에서 14까지 가는데 한번에 1, -1, 5 밖에 못움직인다 했을 때 가장 빠르게 갈 수 있는 횟수는 몇번인가? 라는 문제이다.
이때 트리 형태로 그리면

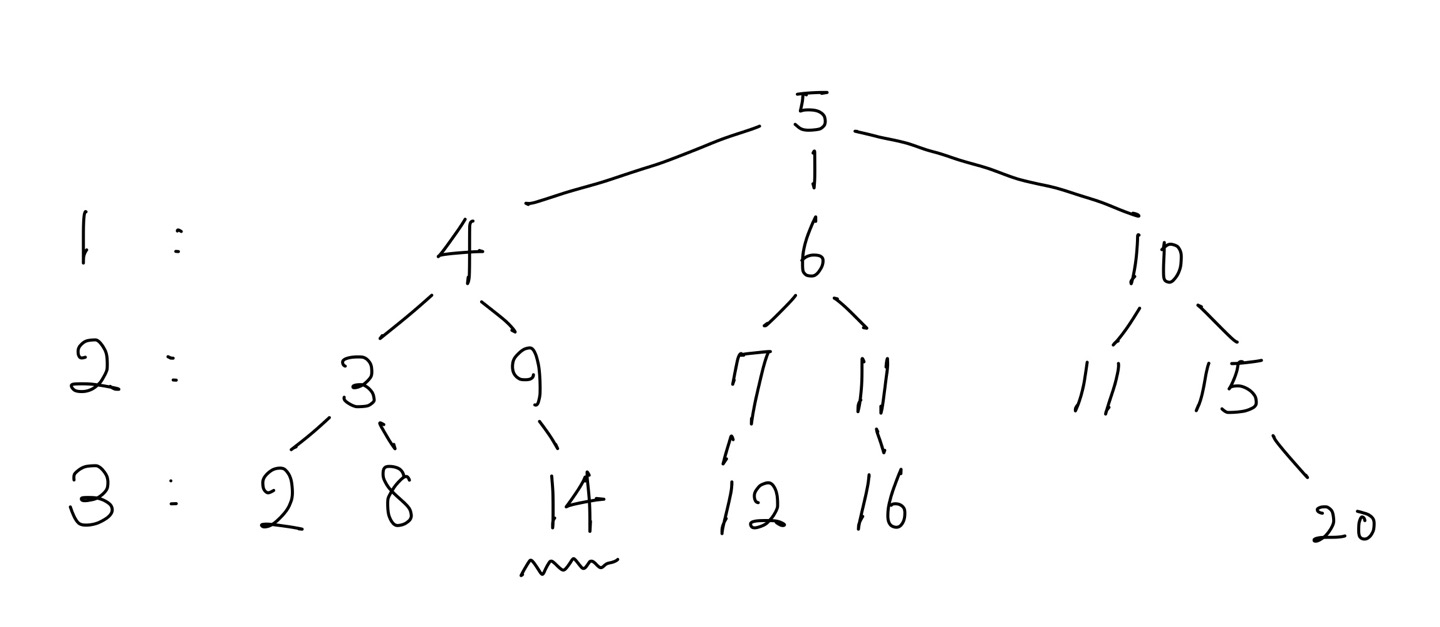
다음과 같이 나오게 되는데, 이 때 3번째에 14라는 수가 처음 등장하는 것을 알 수 있게 된다.

7-12

경로탐색

5개의 노드가 있다면 5*5의 배열을 생성한다. 이 때 각자 1부터 시작하도록 지정하려면 6*6 즉 a[6][6]의 배열을 만들어서 a[1]부터 a[5]까지 선언될 수 있도록 만든다.
그리고 ch[]라는 배열을 만들어 한 번 지나간 노드는 다시 못지나가도록 0과 1을 잘 조절해준다.

public void DFS(int v) {
	if (v == n) answer++; //도착했을 경우
    else {
    	for (int i=1; i<=n; i++){
        	if (graph[v][i] == 1 && ch[i] == 0) { // 경로가 존재하고, 아직 지나가지 않음
            	ch[i] = 1; // 한 번 지나갔어요
                DFS(i); // 다음 경로 찾아요
                ch[i] = 0; // 경로 찾았으니 노드 재사용 가능
            }
        }
    }
}