
Dot Product, Inner Product (내적)
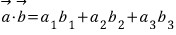
내적이란 두 벡터의 같은 성분끼리의 곱의 합으로, 두 벡터의 곱과 유사하다.
예를 들어 vecotr A(x1, y1)와, vector B(x2, y2)가 있을 때,
두 벡터의 내적인 A · B 는 (x1*x2) + (y1*y2)가 된다.
즉 벡터의 내적은 스칼라값이다.
이 값은, 한 벡터의 방향으로 다른 벡터를 projection투영 시킨 후 곱한 값이다.
내적의 정리1
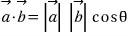
두 벡터의 내적 값은, 두 벡터의 크기와 두 벡터 사이의 각을 곱한 값과 같다.
|a| 는 vector A의 크기이고 θ는 두 벡터가 이루는 각이다.
따름정리
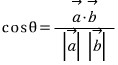
따라서 두 벡터 사이의 cosθ는 위와 같은 정리를 만족한다.
응용: 두 벡터 사이의 각도 구하기 (0 ~ 180도)
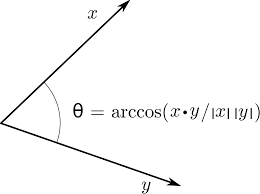
따라서 벡터의 내적을 활용해 두 벡터가 이루는 각을 구할 수 있다.
- 두 벡터의 내적으로 cosθ 값을 구할 수 있다.
- arccos(cosθ)를 한다면, θ 값을 도출할 수 있다.
- 이 때 normalized된 단위벡터를 활용한다면 arccos에 넣을 값이 간결해지므로 용이하다
❕두 벡터 사이의 값이 180도가 넘눈다면, 외적 등을 활용해 추가적인 연산을 해야함
❕두 벡터 사이의 값은 arctan으로도 구할 수 있음
❕ 응용문제: https://rangsub.tistory.com/15
내적의 정리2
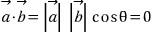
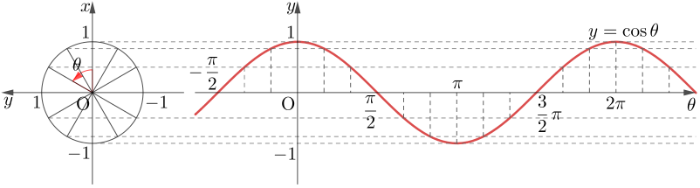
두 벡터의 내적 값으로 두 벡터의 유사도(진행방향 사이의 관계)를 판단할 수 있다.
cos의 그래프를 떠올리면 쉽게 연상 가능하다.
- 내적 값이 0이라면, 두 벡터는 수직이다
- 내적 값이 양수라면, 두 벡터 사이의 각은 90도보다 작다
- 내적 값이 음수라면, 두 벡터 사이의 값은 90도보다 크다
Projection
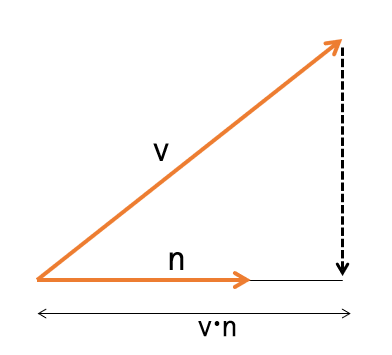
두 벡터의 내적은 개념적으로 한 벡터의 방향으로 다른 벡터를 투영시켜 곱한다.
즉, 어떤 vector V를 단위벡터 N에 내적한다면, V의 N의 방향으로의 길이를 구할 수 있다.
내적을 사용하는 이유
두 벡터 사이의 각도를 구하려면 arccos 함수를 사용해야 하는데,
삼각함수를 남발하면 프로그램의 성능이 하락할 수 있으므로
몇 번의 곱셈과 덧셈으로 끝나는 내적을 사용하는 것이 이득이다.
내적의 응용사례
- 3D에서 면이 빛을 받음을 계산할 때 (즉, 명암처리 시)
- 3D에서 면이 카메라를 향하는지 계산할 때 (즉, Normal 판단 시)
- 반사 벡터를 구할 때
- 그림자를 구할 때
References
[1] 내적의 정의 : https://m.blog.naver.com/mindo1103/90103350914
[2] 두 벡터의 사이각 구하기 : https://asteriskhun.tistory.com/40
[3] 벡터의 내적 응용문제 : https://rangsub.tistory.com/15
[4] 반사벡터 구하기 : https://novemberfirst.tistory.com/112
