문제
A peak element is an element that is strictly greater than its neighbors.
Given an integer array
nums, find a peak element, and return its index. If the array contains multiple peaks, return the index to any of the peaks.You may imagine that
nums[-1] = nums[n] = -∞.You must write an algorithm that runs in
O(log n)time.Example 1:
Input: nums = [1,2,3,1] Output: 2 Explanation: 3 is a peak element and your function should return the index number 2.Example 2:
Input: nums = [1,2,1,3,5,6,4] Output: 5 Explanation: Your function can return either index number 1 where the peak element is 2, or index number 5 where the peak element is 6.Constraints:
1 <= nums.length <= 1000
-231 <=nums[i]<= 231 - 1
nums[i] != nums[i + 1]for all validi.
Python 풀이
class Solution: def findPeakElement(self, nums: List[int]) -> int: left = 0 right = len(nums)-1 while left<right: mid = (left + right) // 2 if nums[mid] < nums[mid+1]: left = mid+1 else: right = mid return left
문제 설명
Peak Element: 봉오리처럼 우뚝 솟아있는 요소
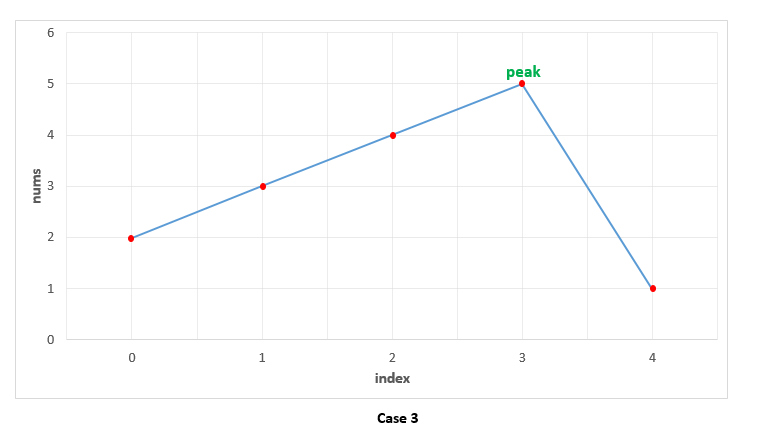
위에 사진과 같이 이웃한 양 옆의 숫자와 비교했을 때 두 숫자보다 더 크면 peak element이다. 이런 지점을 찾는 문제이다. 알파벳 대문자 'M' 모양으로 peak element가 두 개 이상인 곳이 있을 때는 아무 지점이나 답으로 적으면 된다. (인덱스를 출력해야함)
접근법
처음에는
'그냥 리스트에서 가장 큰 숫자의 인덱스를 출력하면 되는 것 아닌가?'
라는 말도 안되는 생각으로 return nums.index(max(nums)) 를 해보았는데 성공했다....ㄷㄷ
그러나 문제에서 O(log n)안으로 풀라고 나와있기 때문에 풀이가 성공할지언정 완벽한 답은 아니다. 따라서 이 문제는 다른 방법을 이용해서 풀어야 한다.
이분 탐색(이진 탐색): 정렬된 데이터에서 절반씩 나누어가며 원하는 데이터를 찾는 알고리즘
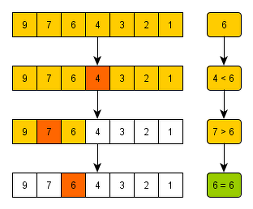
위 사진에서 보는 것과 같이 리스트에 숫자가 들어있는데, 리스트에서 6을 찾고싶다.
left = 0,right = 6(리스트의 length - 1)
- 가장 왼쪽 인덱스와 오른쪽 인덱스를 먼저 설정한다.
mid = (left + right) / 2
- 가운데 값을 저장한다.
mid = 3이 된다.
- 찾는 숫자와
mid인덱스를 가진 숫자를 비교한다.
4 < 6
- 6은 4보다 크니까 4보다 오른쪽에 있는 숫자들은 비교할 필요없이 다 작을 것이다. 따라서
right = mid로 설정한다.
- 리스트의
mid인덱스를 가진 숫자가 4이므로 오른쪽은 더이상 볼 필요가 없다. 따라서 가장 오른쪽을 이제mid로 설정해 준다.
left = 0,right = 3
mid = (left + right) / 2(파이썬에서는mid = (left + right) // 2)
mid = 1이 된다.
- 인덱스가 1인 숫자는 7이다. 7은 6보다 크다.
6 < 7
- 6을 찾는 것이므로 7보다 큰 부분인 7의 왼쪽 숫자들은 볼 필요가 없다.
left = mid + 1로 설정한다.
left = 2,right = 3
mid = 2가 된다. 인덱스가 2인 숫자는 6이고 우리가 찾는 숫자이므로 여기서 알고리즘이 종료된다.
이런 식으로 두 부분으로 나누어 비교한다. 처음부터 끝까지 비교하면 n개의 숫자가 있을 경우 n번을 다 비교해야 하지만, 이분 탐색을 사용하면 O(log n)만에 찾을 수 있다.
코드 설명
class Solution:
def findPeakElement(self, nums: List[int]) -> int:
left = 0
right = len(nums)-1
while left<right:
mid = (left + right) // 2
if nums[mid] < nums[mid+1]:
left = mid+1
else:
right = mid
return leftleft = 0,right = len(nums)-1로 설정- left가 커지고 right가 작아지고 하다보면 left와 right가 같아질 때가 있다. 그 때가 원하는 값을 찾은 경우이므로 같아지면 반복문이 종료된다.
mid = (left + right) // 2: 가운데 지점- 현재 값이 오른쪽 값보다 작다면,
left = mid + 1로 설정 - 더 크다면,
right = mid로 설정 - 반복문이 종료되면
left가 정답.
정렬이 안되어 있는데?
원래 이분 탐색을 진행할 경우 오름차순 또는 내림차순으로 정렬되어 있어야 한다. 그렇지 않으면 절반을 나눴을 때 오른쪽에 원하는 값이 있는데 정렬이 안되어 있어서 오른쪽을 버리고 왼쪽을 탐색해버릴 수도 있기 때문이다.
그런데 이 문제는 정렬이 되어있지 않다. 그런데 왜 이분 탐색으로 풀었을까?
peak point인 아무 지점이나 찾는 것이기 때문에 상관이 없다.
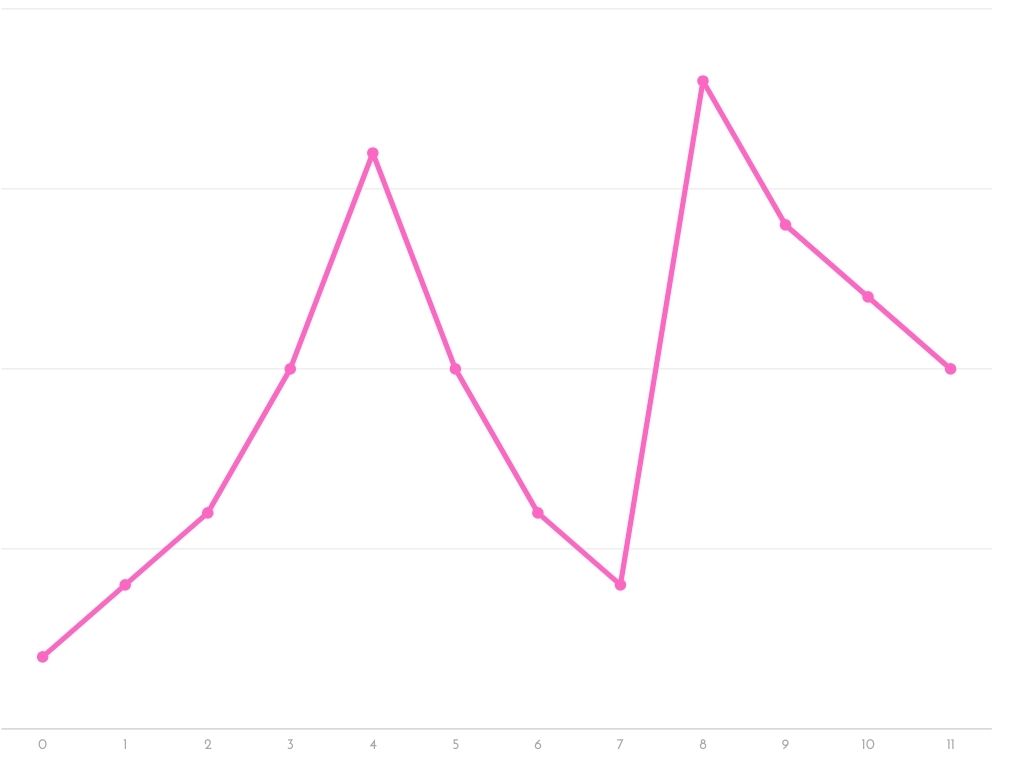
보이는 것과 같이 두개의 peak point가 있을 때, 이 데이터들은 정렬되지 않았다. 그렇지만 각 peak point를 기준으로 왼쪽과 오른쪽은 정렬된 데이터라고 볼 수 있다.
다르게 얘기해서, 정렬된 데이터들의 집합이라고 보면 된다.
0번 ~ 4번, 4번 ~ 7번, 7번 ~ 8번, 8번 ~ 11번
이렇게 4개의 집합을 따로 따로 보면 정렬된 데이터이다.