LeetCode | 235. Lowest Common Ancestor of a Binary Search Tree

송치헌·2021년 7월 20일

Algorithm | LeetCode

목록 보기

9/15

문제

Given a binary search tree (BST), find the lowest common ancestor (LCA) of two given nodes in the BST.

According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”

Example 1:
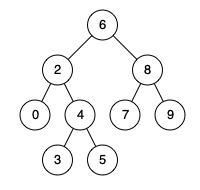
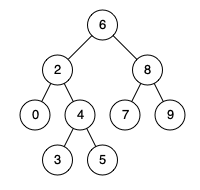
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
Output: 6
Explanation: The LCA of nodes 2 and 8 is 6.
Example 2:
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
Output: 2
Explanation: The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.
Example 3:
Input: root = [2,1], p = 2, q = 1
Output: 2
Constraints:

The number of nodes in the tree is in the range $[2, 10^5]$ .
$-10^9 <=$ Node.val $<= 10^9$
All Node.val are unique.
p != q
p and q will exist in the BST.

Python 풀이

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        if root.val == p.val or root.val == q.val:
            return root
       
        min_val = min(p.val, q.val)
        max_val = max(p.val, q.val)
       
        if min_val < root.val < max_val:
            return root
        elif root.val < min_val:
            return self.lowestCommonAncestor(root.right, p, q)
        else:
            return self.lowestCommonAncestor(root.left, p, q)

문제 설명

이진 탐색 트리에서 주어진 두 노드의 LCA(최소 공통 조상)을 찾는 문제이다. 참고로 어떤 노드던지 자기 자신이 조상이 될 수 있다. 나의 조상이 나라는 뜻이다...아무튼 Example 1 을 보면

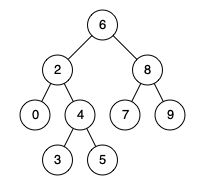
p = 2, q = 8 2와 8의 최소 공통 조상은 6이다.

접근법

이진 탐색 트리(BST)는 한가지 특징이 있는데 어떤 노드의 왼쪽 자식 노드들은 항상 그 노드의 값보다 작고 오른쪽 자식 노드들은 항상 그 노드의 값보다 크다. 예제의 사진을 보면 이해가 되는데, root노드인 6을 보면 왼쪽에 있는 자식들은 다 6보다 작다. 반면에 오른쪽 자식들은 다 6보다 크다.
이걸 이용해서 문제를 풀 수 있다.

먼저 가장 위에서 부터 검사하며 내려올 것이다.
이 문제에서는 4가지 방향이 있다.
p < q 라고 가정하고 설명하겠다.

현재 검사할 노드(t)가 p나 q와 같은가?

현재 검사할 노드(t)가 p < t < q 인가?

현재 검사할 노드(t)가 t < p 인가?

현재 검사할 노드(t)가 t > q 인가?

예제로 더 정확히 설명해보면

Example 1
root = 6, p = 2, q = 8

2번(p < t < q)을 만족하므로 정답은 현재 검사하는 노드 6이 정답이다.

Example 2
root = 6, p = 2, q = 4

4번(t > q)을 만족하므로 LCA를 찾을 두 노드는 전부 루트 노드(6)의 왼쪽에 있다. 이진 트리이기 때문에 바로 아래 자식 노드가 왼쪽과 오른쪽 2개밖에 없는 것을 볼 수 있다. 따라서 검사할 루트 노드가 왼쪽 자식 노드로 바뀐다.

root = 2, p = 2, q = 4

이번에는 1번(t == p or t == q)을 만족하므로 현재 검사하는 노드(2)가 정답이 된다.

코드 설명

가장 처음에 나오는

        if root.val == p.val or root.val == q.val:
            return root

이 부분은 위에서 설명하는 1번 케이스이다. 이 부분에 해당하면 현재 검사하는 루트 노드가 정답이 된다.

그리고 나서 min, max함수로 p와q의 최소 최대를 나눠 준다. (각 노드의 값들은 유니크하다는 조건이 있기 때문에 최대 최소가 나뉠 수 있다.)

그 다음에 나오는

        if min_val < root.val < max_val:
                    return root

이 부분은 2번 케이스에 해당한다. 이 부분에 해당해도 현재 검사하는 루트 노드가 정답이다.

        elif root.val < min_val:
            return self.lowestCommonAncestor(root.right, p, q)
        else:
            return self.lowestCommonAncestor(root.left, p, q)

이 부분은 3번, 4번 케이스에 해당하는 부분이다.
만약 현재 검사하는 루트 노드의 값이 LCA를 찾을 두 노드 중에 가장 작은 값보다 작다면 현재 함수(lowestCommonAncestor)를 다시 호출한다. 근데 바뀌는 부분이 있다면 (root.right, p, q) 이 부분인데, 검사할 루트 노드를 오른쪽 자식 노드로 바꾼다는 얘기이다. (그 전에 검사했던 루트 노드는 LCA가 아니므로 루트 노드를 오른쪽 한칸 아래에 있는 자식 노드로 바꾼다는 뜻)

반대로 최대값보다 크다면 두 노드는 둘 다 현재 루트노드의 왼쪽 자식에 있다는 뜻이므로 오른쪽은 볼 필요가 없다. 따라서 루트노드가 왼쪽 한칸 아래에 있는 자식 노드로 옮겨간다.