문제

A message containing letters from A-Z can be encoded into numbers using the following mapping:

'A' -> "1"
'B' -> "2"
...
'Z' -> "26"

To decode an encoded message, all the digits must be grouped then mapped back into letters using the reverse of the mapping above (there may be multiple ways). For example, "11106" can be mapped into:

"AAJF" with the grouping (1 1 10 6)
"KJF" with the grouping (11 10 6)
Note that the grouping (1 11 06) is invalid because "06" cannot be mapped into 'F' since "6" is different from "06".

In addition to the mapping above, an encoded message may contain the '*' character, which can represent any digit from '1' to '9' ('0' is excluded). For example, the encoded message "1*" may represent any of the encoded messages "11", "12", "13", "14", "15", "16", "17", "18", or "19". Decoding "1*" is equivalent to decoding any of the encoded messages it can represent.

Given a string s containing digits and the '*' character, return the number of ways to decode it.

Since the answer may be very large, return it modulo 109 + 7.

Example 1:

Input: s = "*"
Output: 9
Explanation: The encoded message can represent any of the encoded messages "1", "2", "3", "4", "5", "6", "7", "8", or "9".
Each of these can be decoded to the strings "A", "B", "C", "D", "E", "F", "G", "H", and "I" respectively.
Hence, there are a total of 9 ways to decode "*".

Example 2:

Input: s = "1*"
Output: 18
Explanation: The encoded message can represent any of the encoded messages "11", "12", "13", "14", "15", "16", "17", "18", or "19".
Each of these encoded messages have 2 ways to be decoded (e.g. "11" can be decoded to "AA" or "K").
Hence, there are a total of 9 * 2 = 18 ways to decode "1*".

Example 3:

Input: s = "2*"
Output: 15
Explanation: The encoded message can represent any of the encoded messages "21", "22", "23", "24", "25", "26", "27", "28", or "29".
"21", "22", "23", "24", "25", and "26" have 2 ways of being decoded, but "27", "28", and "29" only have 1 way.
Hence, there are a total of (6 * 2) + (3 * 1) = 12 + 3 = 15 ways to decode "2*".

Constraints:

$1 <=$ s.length $<= 10^5$
s[i] is a digit or '*'.

Python 풀이

class Solution:    
    def numDecodings(self, s: str) -> int:
        dp = [0 for _ in range(100002)]
        dp[0] = 1
        mod = 1000000000 + 7
        slen = len(s)
        if slen==1:
            if s=='*': return 9%mod
            elif s=='0': return 0%mod
            else: return 1%mod
        if s[0]=='*':
            dp[1] = 9%mod
        elif s[0]=='0':
            dp[1] = 0%mod
        else:
            dp[1] = 1%mod

        for k in range(1, slen):
            if s[k]=='*':
                dp[k+1] = (9 * dp[k])%mod
                if s[k-1]=='*':
                    dp[k+1] += (15 * dp[k-1])%mod
                elif s[k-1]=='1':
                    dp[k+1] += (9 * dp[k-1])%mod
                elif s[k-1]=='2':
                    dp[k+1] += (6 * dp[k-1])%mod
            else:
                if s[k]=='0':
                    dp[k+1] = 0%mod
                else:
                    dp[k+1] = dp[k]%mod
                if s[k-1]=='*':
                    if '0'<=s[k]<='6':
                        dp[k+1] += (2 * dp[k-1])%mod
                    else:
                        dp[k+1] += dp[k-1]%mod
                elif s[k-1]=='1':
                    dp[k+1] += dp[k-1]%mod
                elif s[k-1]=='2':
                    if '0'<=s[k]<='6':
                        dp[k+1] += dp[k-1]%mod
                    else:
                        dp[k+1] += 0%mod             
        return dp[slen]%mod

정말이지 쉬운 것 같으면서도 머리가 깨지는 문제였다...
알고리즘을 많이 풀어본 사람은 금방 눈치채겠지만 입력 문자열의 길이가 $10^5$ 인걸 보면 DP가 떠오를 것이다. (모든 문제가 다 그런 것은 아님)
실제로 문제를 읽어보면서도 DP로 풀어야겠다고 감이 잡혔는데 식을 어떻게 세워야 하는지 감이 안잡혔다. 경우의 수가 너무 많았다.

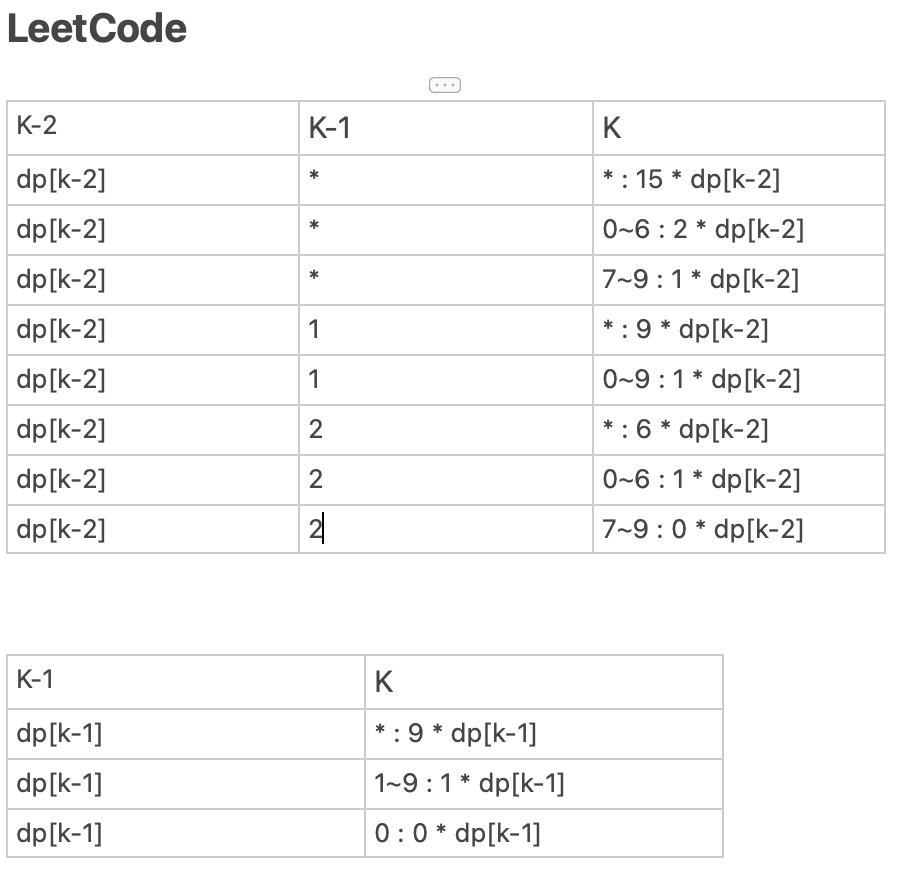
메모장에 이런식으로 경우의 수를 다 정리하여 풀었다.

문제 설명

문자열 s가 주어진다. 이 문자열은 숫자(0~9) 또는 '*' 기호로 이루어져 있다. 한편, 알파벳 대문자는 숫자와 매핑된다.
A = 1
B = 2
...
Z = 26
이렇게 26개의 알파벳이 1번부터 26번까지 번호가 매겨져있다.
이제 주어진 문자열을 쪼개든 조합하든 알파벳으로 decode하는 경우의 수를 구하는 문제이다.
예를 들어, 1312라는 숫자는 1, 3, 1, 2 로 쪼갤 수 있고 각 숫자는 A, C, A, B가 된다.
또한 1, 3, 12이렇게 쪼갤 수도 있다. A, C, L이 된다. 정리하면

• 1312
  • 1, 3, 1, 2 --> A, C, A, B
  • 1, 3, 12      --> A, C, L
  • 13, 1, 2      --> M, A, B
  • 13, 12           --> M, L

이렇게 4가지의 경우의 수가 나오며 이 경우는 답이 4가 된다.
1, 31, 2 이렇게 묶는 경우는 불가능하다. 31에 매치되는 알파벳이 없기 때문이다.

또 문자열에는 '*'도 있을 수 있다. '*'는 0을 제외한 모든 숫자로 표현 가능하다.
예를 들어, 1* 이면 11, 12, ..., 19 로 다 표현이 가능하다. 1, 1은 A, A이고 11은 K이므로 2가지, 1, 2는 A, B이고 12는 L이므로 2가지...이렇게 9개 전부 해주면 총 경우의 수는 18개이다.

접근법

121이라는 숫자를 보자.

1 / 2 / 1
1 / 21
12 / 1

이렇게 총 3가지 경우로 나뉜다.
그럼 이제 1211이라는 숫자를 보자.

1 / 2 / 1 / 1
1 / 2 / 11
1 / 21 / 1
12 / 1 / 1
12 / 11

이렇게 5가지 경우가 나온다. 1211은 121 뒤에 1만 붙인 것이므로 뒤에 있는 1을 N으로 바꿔보자.

1 / 2 / 1 / N
1 / 2 / 1N
1 / 21 / N
12 / 1 / N
12 / 1N

이걸 순서를 바꿔서 다시 보면

1 / 2 / 1 / N
1 / 21 / N
12 / 1 / N
1 / 2 / 1N
12 / 1N

이렇게 된다. 위에 있는 121의 경우의 수와 비교해보자.

121	1211
1 / 2 / 1	1 / 2 / 1 / N
1 / 21	1 / 21 / N
12 / 1	12 / 1 / N
-	1 / 2 / 1N
-	12 / 1N

전에 있던 숫자 뒤에 그냥 N을 추가한 것 + 맨 마지막에서 두번째 숫자와 결합한 형태

이런식으로 1211은 121의 경우의 수에서 몇가지만 더 추가되는 형태이다.
우리는 이런 문제를 DP(Dynamic Programing) 알고리즘을 이용하여 풀 수있다. DP(다이나믹 프로그래밍 혹은 동적 프로그래밍)는 이전에 구한 해를 가지고 정답을 구하는 것이다.

그냥 쉽게 얘기해서 해를 몇개 구해 놓으면 그걸 가지고 원하는 정답을 구하는 것인데, 대표적인 문제가 Fibonacci수열이다. 보통 재귀함수 문제를 풀 때 단골로 나오는 친구이다.

def Fibo(n):
    return Fibo(n-2) + Fibo(n-1) if n>=2 else n
print(Fibo(10))

보통 이런 식으로 구현하는데(실행은 안해보고 방금 대충 짠 코드이다.)
Fibo(10)을 호출하면 함수 안에서 Fibo(8)과 Fibo(9)를 또 호출한다. 그럼 또 안에서 2개씩 호출하고 Fibo(n)을 호출하면 총 $2^n$번 호출한다. 숫자가 커질수록 시간은 엄청나게 오래 걸릴 것이다. 따라서 숫자가 클수록 재귀함수를 이용해서 푸는 것보다 DP를 이용하여 푸는 것이 더 효율적이다.

dp = [0] * 1000000
dp[0] = 0
dp[1] = 1
for i in range(2, 1000000):
    dp[i] = dp[i-2] + dp[i-1]

이건 무려 O(n)만에 풀이가 가능하다!

아무튼 DP는 수열에서 많이 봤던 점화식과 비슷하다.

코드 설명

dp를 저장할 리스트를 문자열 최대 길이만큼 만든다.
이제 이 dp에 경우의 수를 저장할 것이다.
문자열의 길이가 5라면

dp[1] = p1
dp[2] = p2
...
dp[5] = p5

이런 식으로 저장되는데,
여기서 p1은 첫번째 문자만 봤을 때 나올 수 있는 경우의 수.
p2는 두번째 문자까지 봤을 때 경우의 수.
p3는 세번째 문자까지 봤을 때 경우의 수.
이런 식으로 마지막 문자열까지 다 훑어봤을 때 경우의 수를 저장해 나갈 것이다.

mod는 숫자가 너무 커지는 것을 방지하기 위해 $10^9+7$ 로 나눈 나머지를 출력하라고 했기 때문에 mod로 저장해 준다.

그리고 문자열의 길이가 1일 때와 2이상일 때를 나눠서 코딩해 주면 된다. 이제 본격적으로 문자를 하나씩 쪼개보면서 풀어주면 되는데

여기 내가 만든 표를 보고 그대로 코드로 옮기면 된다. 이해 할 필요는 없고 그냥 노가다로 다 구했다...ㅠㅠ