[Chap 1] 소개

Hyungseop Lee·2023년 3월 13일

[Study] Machine Learning

목록 보기

2/9

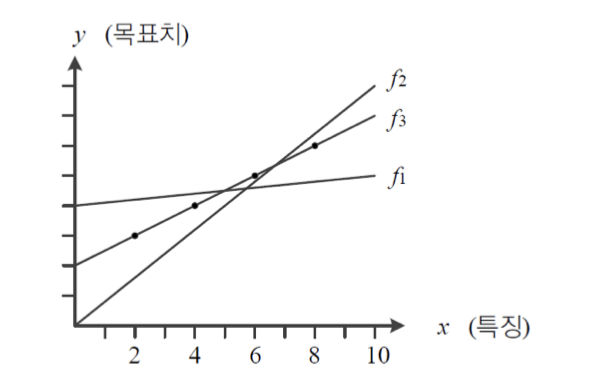
기계 학습이란

기계 학습의 정의

"Programming computers to learn from experience should eventually eliminate the need for much of this detailed programming effort." 컴퓨터가 경험을 통해 학습할 수 있도록 프로그래밍할 수 있다면, 세세하게 프로그래밍해야 하는 번거로움에서 벗어날 수 있다. [Samuel 1959]
"A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E." 어떤 컴퓨터 프로그램이 T라는 작업을 수행한다. 이 프로그램의 성능을 P라는 척도로 평가했을 때 경험 E를 통해 성능이 개선된다면 이 프로그램을 학습을 한다고 말할 수 있다. [Mitchell 1997]

기계 학습을 주제로 한 책에서 말하는 정의들의 공통적 용어는 경험, 성능 개선, 컴퓨터 이다.

즉, 기계 학습이란 특정한 응용 영역에서 발생하는 데이터(경험)을 이용하여 높은 성능으로 문제를 해결하는 컴퓨터 프로그램을 만드는 작업을 뜻한다.

지식기반 방식에서 기계 학습으로의 대전환

1950년대에는 사람이 쉽게 수행하는 문자 인식과 같은 패턴 인식(Pattern Recognition)문제에 도전하였는데, 당시에는 사람의 지식을 추려 프로그램에 심는 접근방식을 사용하였다.

예를 들어, 필기 숫자를 인식한다고 할 때, "구멍이 2개이고 중간 부분이 홀쭉하며, 맨 위와 아래가 둥근 모양이라면 8이다."라는 규칙을 만들어 사용하는 방식이다.

이러한 방식을 지식기반(Knowledge-based) == 규칙기반(Rule-based)라고 한다.

하지만 오래 지나지 않아 지식기반 방식에 분명한 한계가 있다는 사실을 깨닫게 된다.

깨달음을 요약하자면 "사람은 변화가 심한 장면을 아주 쉽게 인식하지만, 왜 그렇게 인식하는지 서술하지는 못한다"라는 것이다. 사람은 태어나면서 아주 많은 단추르 보면서 단추라는 개념을 학습하고, 아주 많은 개와 고양이를 보면서 이들을 구분하는 기분을 학습한다.

이러한 깨달은 이후에 인공지능의 주도권은 서서히 지식기반 방식에서 기계 학습으로 넘어갔다.
기계 학습은 데이터를 중심으로 하는 접근방식을 채택한다.
인식할 대상을 컴퓨터에 일일이 설명하는 대신, 데이터를 충분히 수집하여 입력한다.

이러한 발상의 전환에 따라 기계 학습은 인공지능을 구현하는 핵심 기술로 발돋움한다.

기계 학습 개념

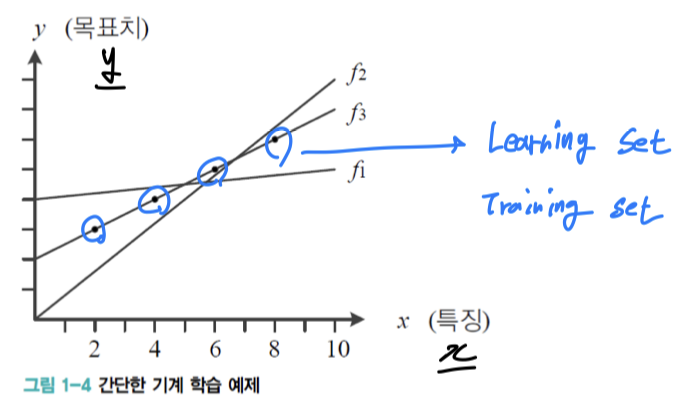
$x$ : feature(특징) ➡️ 대부분 2개 이상의 feature이기 때문에 vector표기
$y$ : target(목표값) ➡️ 대부분 2개 이상의 target이기 때문에 vector표기
O : Learning Set = Training Set = 기계 학습에 주어지는 데이터

회귀와 분류

기계 학습은 예측(Prediction) 문제를 풀며, 예측에는 회귀와 분류가 있다.
실숫값을 예측하는 문제를 회귀(Regression)이라고 한다.
반면에 숫자 인식 문제에서는 10가지 부류 중 하나를 예측해야 하는데,
이렇게 부류를 예측하는 문제를 분류(Classification)이라고 한다.

모델링이란?

위의 그림에서 Training Set의 네 점이 직선을 이루므로 이들의 분포를 직선으로 표현하자.
기계 학습에서는 이러한 의사결정을 모델로 직선을 선택했다 라고 한다.
점들이 좀 더 복잡한 비선형 분포를 이룬다면 2차 곡선 또는 더 높은 차수의 곡선을 모델로 선택해야 한다.

직선이라는 모델은 다음과 같은 식으로 표현할 수 있다.

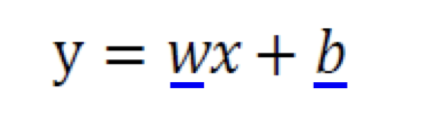
$w, b$ 라는 매개변수(Parameter)를 가진다.

기계 학습이란 가장 정확하게 예측할 수 있는, 즉 최적의 매개변수값을 찾는 작업이다.

위의 그림에서는 $f_3$ 이 최적의 모델이고, $w = 0.5, b = 2.0$ 의 매개변수를 갖는다.

학습이란?

처음에 최적의 Parameter를 알 수 없어서 임의의 값으로 $f_1$ 이 되었는데
$f_2$ 를 거쳐 $f_3$ 에 도달했다면, 모델은 성능이 점점 개선되는 과정을 거쳐 최적의 상태에 도달했다고 말할 수 있다.
이러한 작업을 학습(Learning) 또는 훈련(Training)이라고 한다.

테스트란?

학습을 마치면 그때부터 학습된 모델을 이용하여 예측할 수 있다.

이처럼 Training Set에 없는 새로운 Sample에 대한 목표값을 예측하는 과정을 테스트(Test)라고 한다.
새로운 Sample을 가진 데이터셋을 테스트셋(Test Set)이라 한다.
또한 Train Set과 Test Set을 합쳐 데이터베이스라 한다.

기계 학습의 최종 목표는 Training Set에 없는 새로운 Sample(Test Set)에 대한 오류를 최소화하는 것이다.

Test Set에 대해 높은 성능을 일반화 능력(Generalization)이라 한다.

특징 공간에 대한 이해

1차원과 2차원 특징 공간

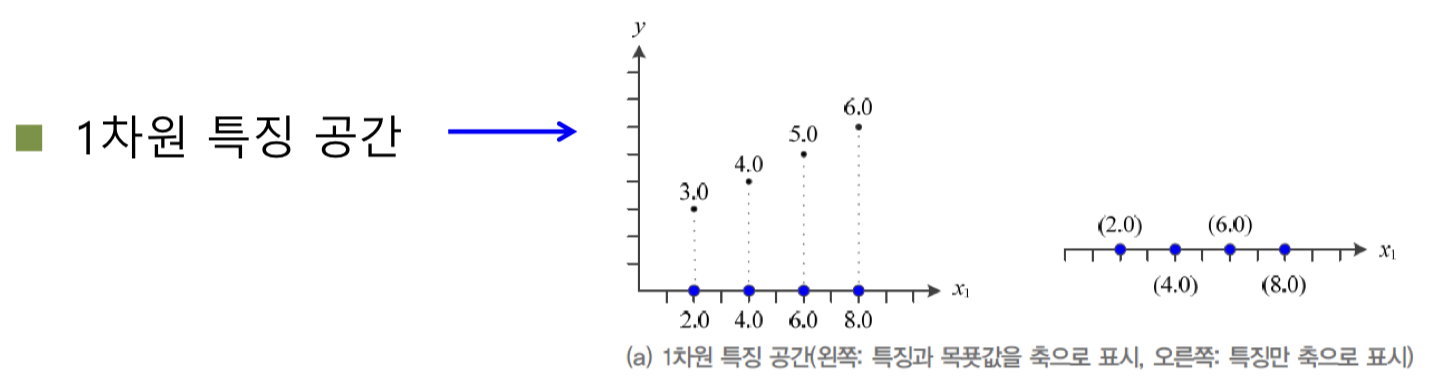
feature $x_1$ 과 target $y$ 에 대한 그래프를
feature $x1$ 에만 축을 배정하여 다시 그릴 수 있다.

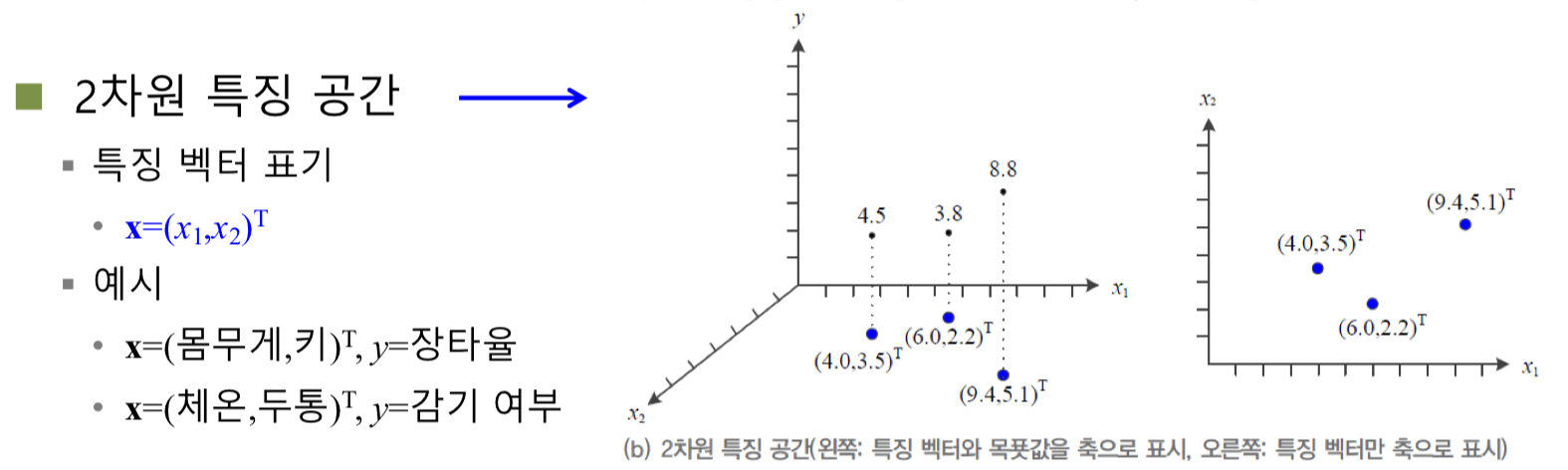
feature $x_1, x_2$ 과 target $y$ 에 대한 그래프를
feature $x_1, x_2$ 에만 축을 배정하여 다시 그릴 수 있다.

다차원 특징 공간

MNIST 데이터베이스는 필기 숫자를 제공하는데,
Sample을 28*28 크기의 비트맵으로 표현한다.
따라서 784개의 화소가 784차원의 특징 공간을 형성한다.
이 경우 목푯값은 0~9의 10개 부류 중 하나이다.

이를 식으로 표현하면 d차원 데이터를 $x = (x_1, x_2, ..., x_d)^T$ 로 표기한다.

차원이 증가하면 모델의 매개변수 개수가 함께 증가한다.

만일 2차 곡선을 모델로 선택한다면 매개변수의 개수는 더 증가한다.

특징 공간 변환과 표현 학습

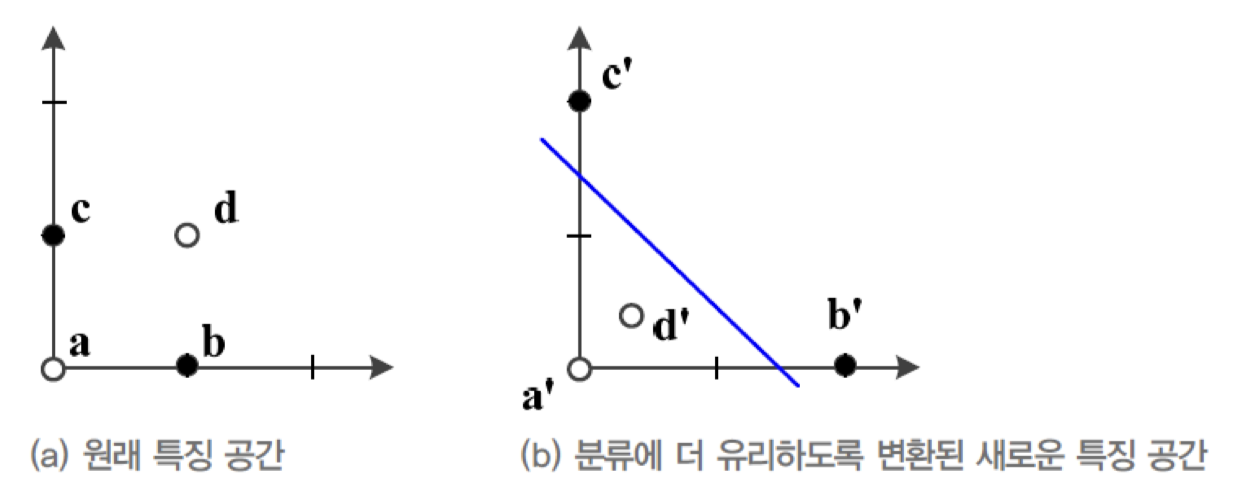
위의 그림은 2차원 특징 공간에 분포된 4개의 Sample이다.

(a)에서 2개의 부류로 Classification하는 문제로 간주하여 $a$ , $d$ 가 하나의 부류에 속하고,
$b$ , $c$ 가 나머지 부류에 속한다고 가정하자.
(a) : 원래 특징 공간에서 직선 모델로는 두 부류를 100% 정확하게 Classification할 수 없다.
어떠한 직선을 사용하더라도 최고 정확률은 75%에 불과.

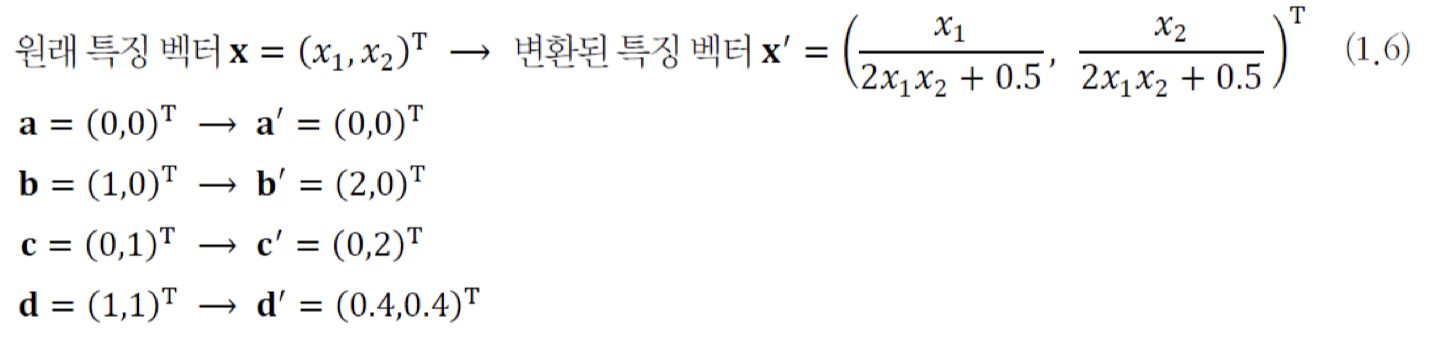
(b) : (a)를 식(1.6)을 이용하여 변환해 보자.
변환 후 4개의 Sample은 $a'$ , $b'$ , $c'$ , $d'$ 라는 새로운 특징 벡터를 갖는다.
이러한 새로운 분포에서는 직선 모델을 활용하여 100% 정확하게 Classification할 수 있다.
실제 세계에세 발생하는 고차원 데이터 분포에서는 표현 학습 알고리즘을 사용해야 한다.
딥러닝은 신경망 구조에 여러 은닉층을 두고, 왼쪽 은닉층에서는 저급 특징을 추출하고 오른쪽으로 갈수록 고급 특징을 추출한다.
ex) 영상을 인식할 때 모든 영상에 공통으로 나타나는 에지나 구석점 등이 저급 특징에 해당하고, 저급 특징이 결합한 얼굴이나 바퀴 등이 고급 특징에 해당한다.

이처럼 현대의 기계 학습은 좋은 특징 공간을 찾아내는 작업을 매우 중요하게 취급하는데, 좋은 특징 공간을 자동으로 찾아낸다는 뜻에서 표현 학습(Representation Learning)이라는 용어를 사용한다.

차원의 저주(Curse of dimensionality)

하지만 고차원이 되면서 현실적인 문제가 발생한다.

예를 들어, 4차원인 Iris 데이터에서 네 축을 각각 100개 구간으로 나눈다면 전체 공간이 $100^4$ , 즉 1억 개의 칸으로 나뉜다. Iris는 150개의 Sample을 갖고 있는데, 1억 개 칸에 150개 Sample이 분포되는 셈이다.
또 다른 예를 보면,

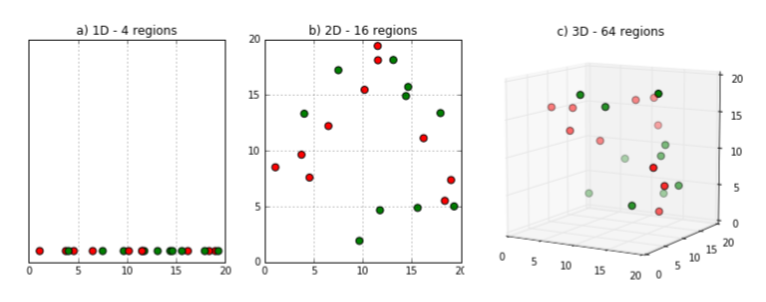
위 그림에서 보는 것과 같이 차원이 증가할수록 빈 공간이 많아진다.

같은 데이터지만 1차원에서는 데이터 밀도가 촘촘했던 것이 2차원, 3차원으로 차원이 커질수록 점점 데이터 간 거리가 멀어진다.
이렇게 차원이 증가하면 빈 공간이 생기는데 빈 공간은 컴퓨터에서 0으로 채워진 공간이다. 즉, 정보가 없는 공간이기 때문에 빈 공간이 많을수록 학습 시켰을 때 모델 성능이 저하될 수밖에 없다.

그렇기 때문에 예측을 위해서는 외삽법(=보외법 : 원래의 관찰 범위를 넘어서서 다른 변수와의 관계에 기초하여 변수의 값을 추정하는 과정)을 많이 사용해야 하는데,

이러면 오버피팅(샘플 데이터에 너무 정확하게 학습이 되었기 때문에, 샘플데이터를 가지고 판단을 하면 100%에 가까운 정확도를 보이지만 다른 데이터를 넣게 되면, 정확도가 급격하게 떨어지는 문제) 발생 가능성이 높다.

이처럼 차원이 증가하면서 학습데이터 수가 차원 수보다 적어져서
성능이 저하되는 현상을 차원의 저주라고 한다.
데이터의 차원이 커지면 그만큼 데이터를 설명하는 변수의 수가 많아지는데, 이에 각 차원 별 충분한 데이터 수가 존재하지 않으면 과적합이 될 수 있기 때문이다.

차원의 저주 문제를 어떻게 해결하는지는 차차 학습하기로 한다.

간단한 기계 학습의 예

다음의 예제는 직선 모델을 이용하여 회귀 문제를 푸는데,
이러한 기계 학습 알고리즘을 선형 회귀(Linear Regression)이라고 한다.

Cost Function

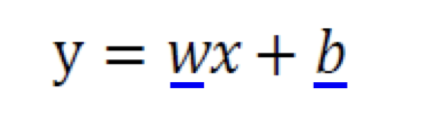
선형 회귀는 위와 같은 식을 사용하므로 추정해야 할 매개변수는 $w$ 와 $b$ , 2개이다.
이 매개변수를 묶어 $\theta = (w, b)^T$ 라고 표기한다.

처음에 최적 parameter를 모르기 때문에 난수를 생성하여 $\theta_1 = (w_1, b_1)^T$ 로 표기한다.
이제 $\theta_1$ 을 개선하여 $\theta_2$ 를 얻고, $\theta_2$ 를 개선하여 $\theta_3$ 를 얻는 방식을 반복하여
최적의 parameter $\hat{\theta}$ 에 도달해야 한다.

이때, 직선을 움직이게 하기 위한 동력인 목적함수 == 비용함수(Cost Function)이 존재한다.

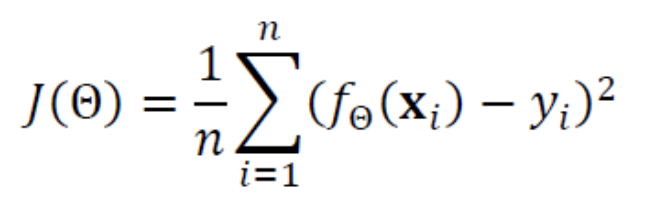
$J(\theta)$ : Cost Function
$f_\theta(x_i)$ : 예측값
$y_i$ : 목표값
$f_\theta(x_i) - y_i$ : $x_i$ 에서의 오차

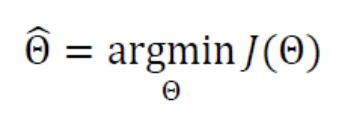
기계 학습 알고리즘은
Cost Function( $J(\theta)$ )값이 작아지는 방향을 찾아매개변수값을 조정하는 일을 반복하는데,
Cost Function이 0.0 또는 0.0에 매우 가까운 값으로 수렴하면 그때 학습을 마친다.

선형 모델의 한계

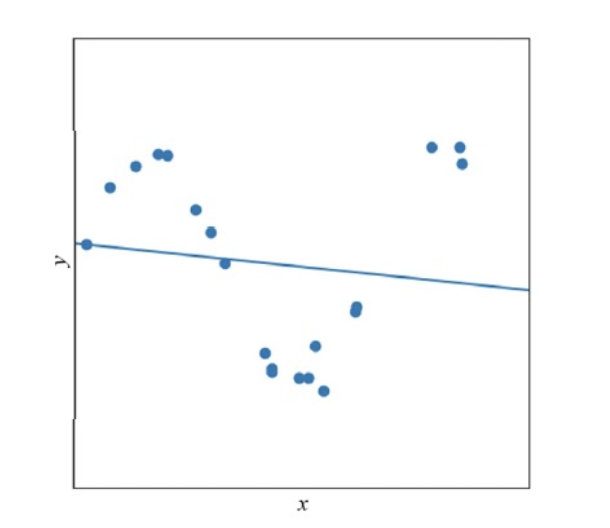
더 현실적인 세계로 보자면,
데이터 자체가 이전과 같이 선형이 아닐 뿐더러 측정 중에 발생한 잡음이 섞여있다.
이 데이터에 직선 근사를 하면, 위와 같이 최적해를 찾더라도 큰 오차를 감수해야 한다.
다음에는 선형 모델을 벗어나 비선형 모델을 사용하는 방식으로 확장한다.

모델 선택

Underfitting

위와 같은 그래프 분포에서는 기계 학습이 최적해를 찾더라도 큰 오차가 생기는데,
이는 모델의 용량이 작기 때문이다.

직선 모델은 데이터가 직선을 이루는 경우에만 수용할 수 있다.
이러한 현상을 과소적합(Underfitting)이라고 한다.

Overfitting

이를 해결하기 위해 쉽게 생각할 수 있는 대안은 더 높은 차원의 다항식,
즉 비선형 모델(nonlinear model)을 사용하는 것이다.

$y$ $=$ $w$ $12$ $x$ $12$ $+$ $w$ $11$ $x$ $11$ $+ ... +$ + $w$ $2$ $x$ $2$ $+$ $w$ $1$ $x$ $1$ $+$ $w$ $0$ $x$ $0$

nonlinear model로 위의 12차 다항식을 선택했다고 가정하자.
1차 미분이 0인 극점이 최대 11개인, 즉 용량이 큰 모델을 가진다.
용량이 커진 대신 추정해야 하는 매개변수가 $w$ $12$ ~ $w$ $0$ 으로 13개나 되어 학습이 어려워진다.

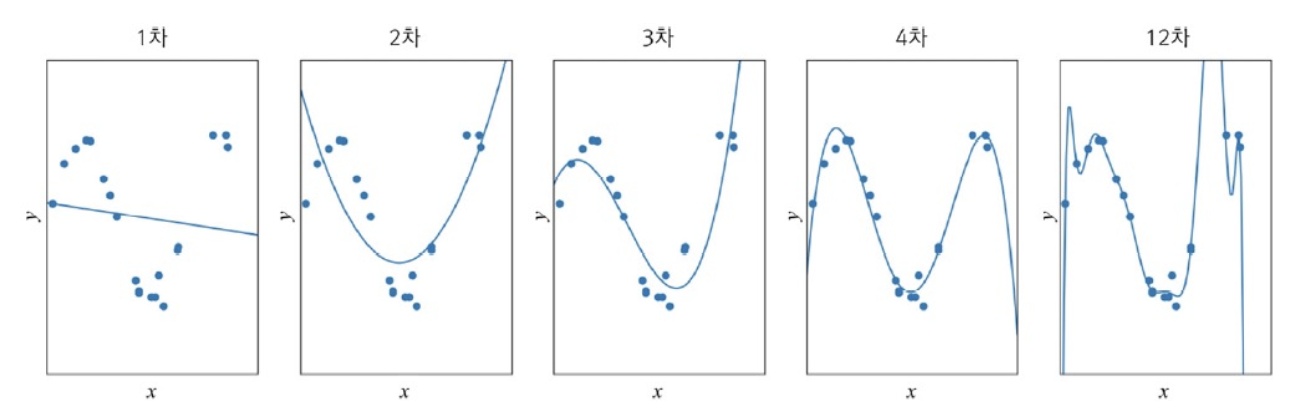
가장 오른쪽 그래프는 12차 nonlinear model을 이용하여 근사화한 결과이다.
Training Set에 있는 점 대부분을 지나며, 지나지 않더라도 아주 가까우므로 완벽에 가깝게 학습했다고 할 수 있다.

하지만 학습된 모델로 Training Set에 없던 새로운 데이터를 예측한다면 어떻게 될까?

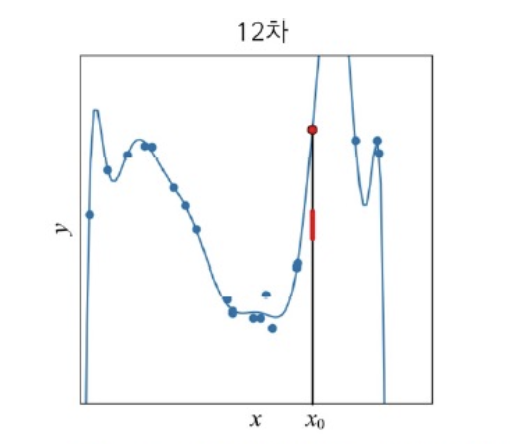
예를 들어, 학습된 곡선으로 $x_0$ 에서 예측한다면 🔴 (빨간색 점)이 도출될 것이다.
하지만 직관적으로 가늠했을 때, l (빨간 선) 범위에서 예측됐어야 합리적일 것이다.

결과적으로 12차 다항식도 모델로 적절하지 않다고 볼 수 있다.

그 이유는 용량이 너무 크기 때문이다.
주어진 데이터 분포와 비교해 용량이 너무 크다 보니 아주 작은 잡음까지 수용한 것이다.
Training Set의 예측에는 완벽에 가깝지만, 새로운 점들이 들어오면 제대로 예측하지 못한다. 이러한 상황을 과잉적합(Overfitting)이라고 한다.

기계 학습의 목표는 Train Set에 없는 새로운 데이터인 Test Set에 대해 높은 성능을 보장하는 프로그램을 만드는 것이다.
이러한 특성을 일반화 능력이라고 한다.

결론 >
1~2차 : Train Set과 Test Set 모두 낮은 성능
3~4차 : Train Set에 대해서 12차보다 낮지만, Test Set에서는 높은 성능 ➡️ 높은 일반화 능력
12차 : Train Set에는 높은 성능을 보이지만, Test Set에서는 낮은 성능 ➡️ 낮은 일반화 능력

Bias & Variance

일반화 능력은 Bias와 Variance라는 개념으로 표현할 수 있다.

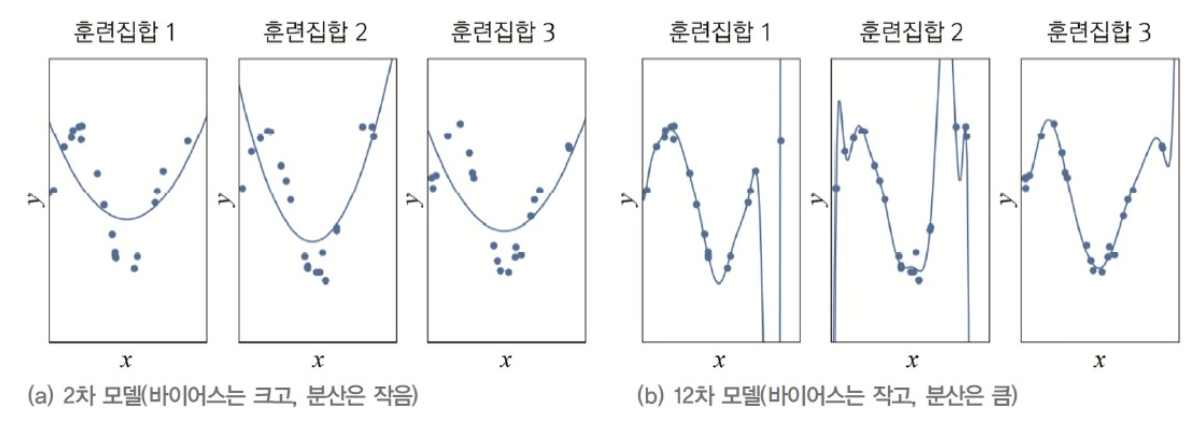
위의 그림은 Train Set을 독립적으로 3번 수집한 후,
Train Set 각각에 대해 2차 모델과 12차 모델을 학습시킨 결과를 보여 준다.

(a)를 보면, 데이터 생성 과정과 2차 다항식 모델 사이에 큰 차이가 있음을 알 수 있다.
이를 Bais가 크다고 표현한다.
반면 Train Set이 바뀌더라도 학습 결과로 얻은 곡선들이 비슷하다는 것을 확인할 수 있다.
이를 Variance가 작다고 표현한다.
➡️ 이처럼 대체로 단순한 모델일수록 Bias는 크고, Variance는 작다.
(b)를 보면, 데이터 생성 과정과 12차 다항식 모델 사이에 큰 차이가 없음을 알 수 있다.
이를 Bais가 작다고 표현한다.
반면 Train Set이 바뀔 때마다 학습 결과로 얻은 곡선들의 모양 크게 요동치는 것을 확인 할 수 있다.
이를 Variance가 크다고 표현한다.
➡️ 이처럼 대체로 복잡한 모델일수록 Bias는 작고, Variance는 크다.

이제 이렇게 말할 수 있다.

기계 학습의 목표는 낮은 Bias와 낮은 Variance를 가진 Predictor를 만드는 것이다.
하지만 Bias와 Variance는 trade-off 관계이기 때문에,
Bias 희생을 최소로 유지하면서 Variance를 최대로 낮추는 전략을 써야 한다.

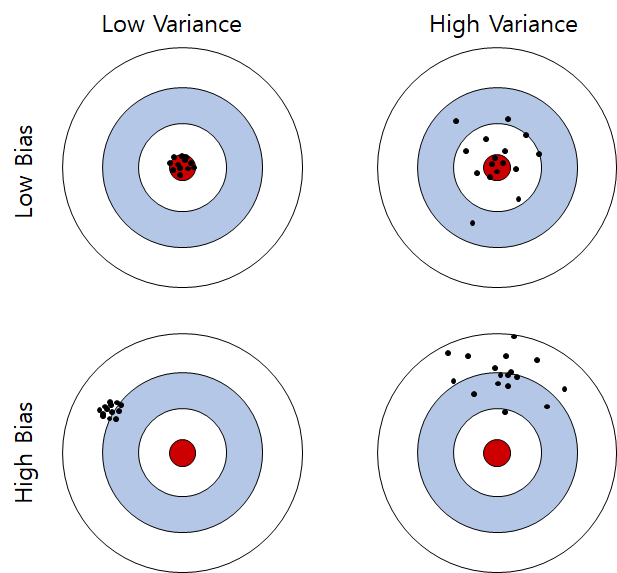
Bias : 점들이 True값과 떨어져 있는 정도
Variance : 점들이 퍼져있는 정도

모델 선택 알고리즘

validation set (검증집합)

지금까지는 Train Set으로 모델을 학습하고, Test Set으로 학습된 모델의 일반화 능력을 측정하였다.
좋은 모델을 알고 있다면 문제는 없지만, 그렇지 않다면 모델집합의 여러 모델을 독립적으로 학습시킨 후 그 중 가장 좋은 모델을 선택해야 한다.

이때 각각의 모델을 비교하는 데에 사용할 별도의 데이터집합을 validation set(검증집합)이라고 한다.

model selection process

cross-validation(교차검증)을 이용한 모델 선택

데이터를 수집하는 것은 비용이 많이 들어 데이터 양이 부족하다.
이러한 상황에서 validation set을 따로 마련하기 힘든데, cross-validation을 이용하면 효과적이다.

K-fold cross validation(k겹 교차검증)

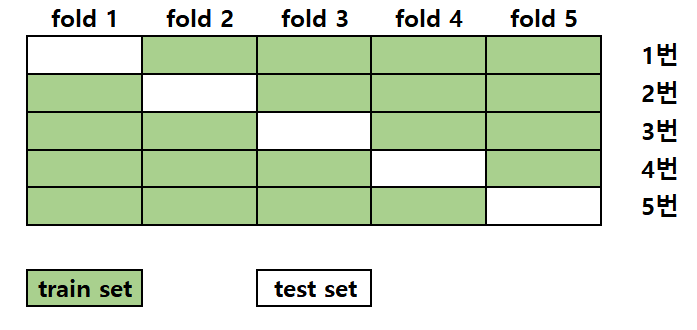
K-fold cross validation(k겹 교차검증)에서는
Train Set을 같은 크기로 나누어 k개의 그룹을 만든다.
그런 다음 k-1개의 Train Set과 1개의 Test Set으로 나눈다.
1개의 Test Set을 k번 달리 하여 모델의 성능을 측정한다.
k개의 성능의 평균을 검증 성능으로 취한다.

boot strap(부트스트랩)을 이용한 모델 선택

Bootstrap은 Train Set으로부터 복원 샘플링을 수행하여 새로운 Train Set을 생성하는 과정.
- 복원 샘플링은 주어진 데이터셋에서 무작위로 샘플을 추출할 때, 한 번 추출한 샘플을 다시 원래 데이터 집합에 반환한 후 다시 추출하는 과정이다.

모델 선택의 한계와 현실적인 해결책

기계 학습에서는 앞으로 다룰 신경망, 강화학습, 확률 그래피컬 모델, SVM, 트리 분류기 등을 사용한다.
이들 각각에 대하여 서로 다른 수없이 많은 모델을 구성할 수 있다.

따라서 가능한 모델은 수없이 많다고 할 수 있다.

현대 기계 학습은 용량이 충분히 큰 모델을 선택한 후, 선택한 모델이 정상을 벗어나지 않도록 여러 가지 규제 기법을 적용하는 현실적인 접근방법을 채택한다.
특히 딥러닝에서는 적절한 규제 기법(Regularization)의 적용이 문제 해결에 아주 중요하다.

기계학습에서 "용량(Capacity)"이란,
모델이 학습할 수 있는 가용한 자유도의 크기를 나타내는 개념.
모델의 용량이 클수록 모델이 복잡한 함수를 모델링할 수 있으며,
작을수록 단순한 함수만 모델링할 수 있다.

규제(Regularization)

규제는 나중에 가중치 벌칙, 조기 멈춤, 데이터 확대, 드롭아웃, 앙상블 등의 다양한 기법을 배울 것이다.

여기서는 규제기법의 전략과 효과를 간략히 공부.

데이터 확대

일반화 능력을 향상시키는 가장 확실한 방법은 데이터를 더 많이 수집하는 것.

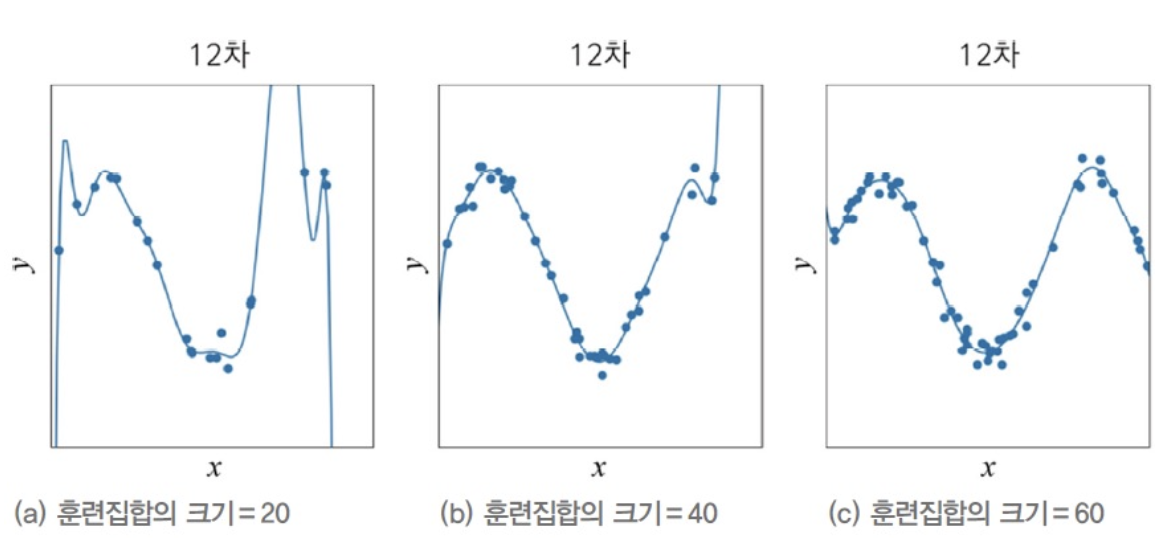
다음과 같이 Train Set의 크기가 20인 (a)는 Overfitting이 심하지만,
Train Set의 크기가 더 커진 60, (b)는 Overfitting이 완화되어
Test Set에 대한 예측을 정확하게 할 것이라고 기대할 수 있다.
하지만 데이터 수집에 많인 비용이 든다.

데이터를 추가로 수집하기 어려운 상황에서는
주로 Train Set에 있는 샘플을 변형함으로써 인위적으로 데이터를 확대하는 방법이 있다.
(이동, 회전, 크기, warping, 잡음 추가 등을 조합)

해당 내용도 5장에서 공부한다.

가중치 감쇠(weight decay)

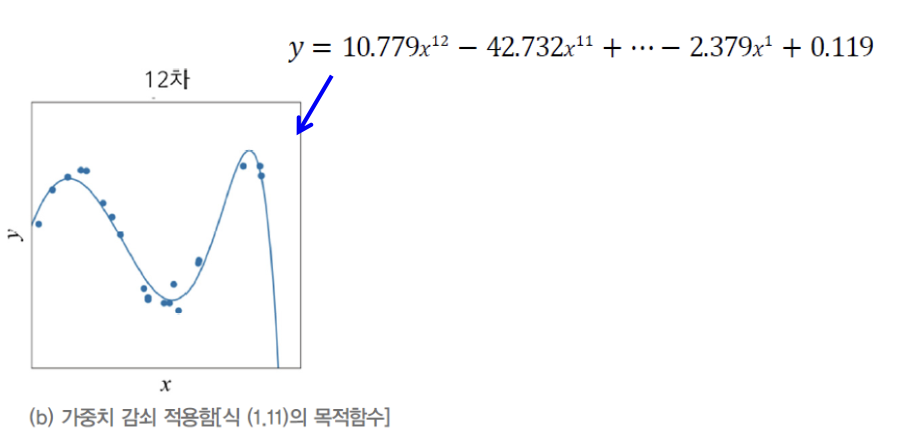
그래프 (a)의 곡선을 굴곡이 매우 심하다 == 곡률(curvature)이 매우 크다.
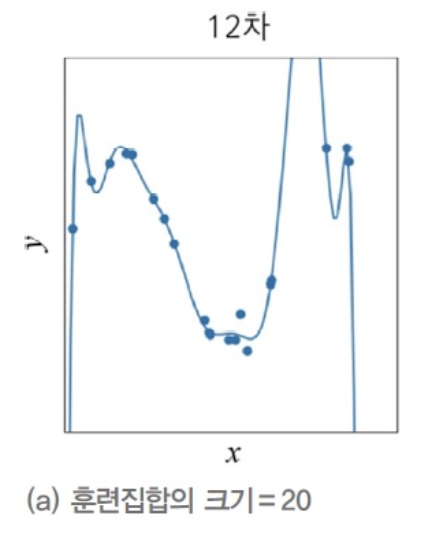
아래의 식은 기계 학습이 찾은 (a)의 곡선의 방정식이다.
방정식에서, Parameter값이 매우 큰 것을 확인할 수 있다.

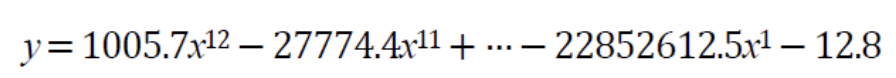
이를 가중치 감쇠(weight decay)라는 규제 기법을 사용하여
가중치를 작게 유지함으로써 일반화 능력을 향상시킬 수 있다.

가중치 감쇠 기법은 2개의 항을 가진 식을 Cost Function으로 사용하는데,
기존의 Cost Function에서 두 번째 항이 추가된 꼴이다.
- 첫번째 항은 이전과 마찬가지로 오류를 줄이는 역할을 한다. (최소점을 찾아가는 동력)
- 가중치의 크기를 나타낸다. 가중치가 클수록 큰 값을 가진다.
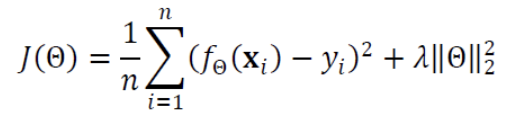
첫번째 항과 두번째 항의 합을 최소화하는 방향으로 학습을 진행하므로,
오류가 적으면서 계수가 작은 해를 찾아준다.

기계 학습 유형

지도 방식에 따른 유형

예전에는 기계 학습 알고리즘을 크게 지도 학습과 비지도 학습으로 구분하였는데,
최근에는 강화 학습이 중요해지면서 지도 학습, 비지도 학습, 강화 학습, 준지도 학습으로 구분한다.

Supervised Learning(지도 학습)

Supervised Learning은 data가 입력(Feature vector)과 출력(목표값=lable) 쌍으로 주어진다.
- $X$ : 입력, $Y$ : 출력
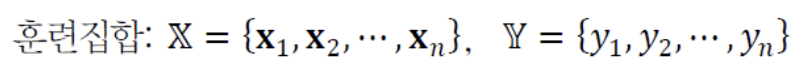
- 이러한 정보를 알려준다는 의미에서 지도라는 명칭을 사용.
- Iris DB에 $X = (5.1, 3.5, 1.4, 0.2), Y=setosa$ 라는 샘플이 있는데,
  이 샘플은 앞으로 꽃받침 길이가 $5.1$ , 너비가 $3.5$ , 꽃잎 길이가 $1.4$ , 너비가 $0.2$ 이거나 유사한 샘플이 입력되었을 때, $setosa$ 라는 부류로 분류하라고 지도하는 것.
지도 학습으로 해결할 수 있는 문제는 Regression과 Classification이 있다.
- Regression은 출력이 연속된 실수로 주어진다.
- Classification은 출력이 이산적인 몇 가지 부류로 주어진다.
최근에는 Regression과 Classification 이외의 새로운 형태의
문제를 Supervised Learning으로 해결하는 사례가 늘고 있다.
딥러닝이 보편화됨에 따라
다양한 문제에 기계 학습을 적용하여 응용 범위를 점점 확대하는 추세.
- ex) Ranking.
  Ranking은 주로 검색에서 활용하는데, 관련 문서를 찾은 후 적합도에 따라 순위를 매겨 사용자에게 제공하는 목적이다.
- ex) 영상 변환.
  영상 변환은 사진과 고흐의 그림을 입력하면 사진을 고흐 화풍의 그림으로 변환하는 응용.

Unsupervised Learning(비지도 학습)

Unsupervised Learning에서는 입력(Feature vector)만 주어진다.
- 그렇다면 출력(lable) 정보가 없는 상화에서 무엇을 할 수 있을까?
  ➡️
  1. Clustering(군집화)를 생각할 수 있다.
    즉, 특징 공간에서 가까이 있는 샘플을 같은 Cluster로 모으는 작업이다.
  2. 특징 공간의 변환이다. 특징 공간의 차원이 커지고 DB 크기가 커지면 사람의 직관에 의존할 수 없게 된다.
    이러한 상황에서 Unsupervised Learning을 이용하여 변환함수를 자동으로 알아낸다.
    6장에서 공부할 Manifold Learning, LLE, IsoMap, t-SNE, PCA는 대표적인 특징 변환 알고리즘이다.
    최근에는 이러한 특징 변환 알고리즘 뿐만 아니라, 신경망의 은닉층에서 일어나는 변환을 모두 포괄하여 Representation Learning(표현 학습) 또는 Feature Learning(특징 학습)이라고 부른다.

Reinforcement Learning(강화 학습)

Reinforcement Learning도 Supervised Learning과 같이
목표값(Lable)을 주어 지도한다.
하지만 목표값의 형태가 Supervised Learning과 많이 다르다.
- ex) 바둑에서 두 사람이 번갈아 수를 놓는데, 각각의 수를 샘플로 볼 수 있다.
  이때 샘플마다 목표값을 주는 Supervised Learning과 달리,
  게임이 다 끝난 후 승패를 따져 승(1) 또는 패(-1), 또는 얻은 점수를 목표값으로 준다.
  연속된 샘플의 열에 목표값 하나만 주는 방식이다.
  따라서 샘플 열에 속한 각각의 샘플에 목표값을 배분하는 알고리즘이 추가로 필요하다.

Semi-supervised Learning(준지도 학습)

입력에 해당하는 $X$ 를 수집하는 일은 상대적으로 쉽지만,
목표값 $Y$ 를 부여하는 일은 사람이 수행해야 하므로 비용이 많이 든다.
- ex) 자연 영상을 수집한다고 하자.
  구글에서 자동으로 $X$ 를 모을 수 있지만,
  이 영상들이 어떤 물체를 포함하는지 알아내 부류 정보를 붙이는 일은 사람이 해야 한다.
Semi-supervised Learning은 소량의 데이터에만 부류 정보를 부여한 후,
부류 정보가 있는 소량의 데이터와
부류 정보가 없는 대량의 데이터를
함께 활용하여 성능 향상을 모색한다.

다양한 기준에 따른 유형

offline learning과 online learning
- 이 책은 오프라인 학습을 다룸
- 온라인 학습은 인터넷 등에서 추가로 발생하는 샘플을 가지고 점증적 학습
deterministic learning과 stochastic learning
- 결정론적에서는 같은 데이터를 가지고 다시 학습하면 같은 예측기가 만들어짐
- 스토캐스틱 학습은 학습 과정에서 난수를 사용하므로
  같은 데이터로 다시 학습하면 다른 예측기가 만들어짐. 보통 예측 과정도 난수 사용
discriminative model learning과 generative model learning
- 분별 모델은 부류 예측에만 관심. 즉 $P(y|x)$ 의 추정에 관심
- 생성 모델은 $P(x)$ 또는 $P(x|y)$ 를 추정함

기계 학습의 기술 추세

기계 학습 알고리즘과 응용이 크고 다양해지고 있다.
고전적으로 분류와 회귀에 집중하던 응용이 변환, 랭킹, 연관, 추천 등의 응용으로 확대되고 있다.
서로 다른 알고리즘 또는 서로 다른 응용이 융합하고 있다.
예를 들어 Image Parsing과 NLP(Natural Language Processing)을 융합하여,
영상을 입력하면 자동으로 영상 내용을 설명하는 문장을 생성하는 응용이다.
최근에는 Deep Learning이 Machine Learning의 주류가 되었다.
딥러닝이 기계학습을 주도하게 된 데에는 GPU라는 값싼 병렬 처리기를 사용할 수 있게 되면서 빛을 보게 된 것이다.
Representation Learning도 매우 중요해졌다.
input feature vector를 새로운 좋은 특징 공간,
즉 좋은 표현으로 변환하면 비교적 단순한 분류기를 쓰더라도 높은 성능을 얻을 수 있다.

Hyungseop Lee

model compression

이전 포스트

Book Info

다음 포스트