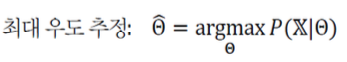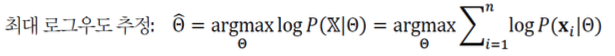확률 기초
Random Variable(확률 변수)
- 윷을 던지면 도, 개, 걸, 윳, 모 5가지 중 하나가 발생.
- 확률을 수식으로 표현하기 위해 5가지 중 한 값을 가지는 변수가 필요.
그 변수를확률 변수(Random Variable)이라고 한다. - 와 같이 소문자로 표기한다.
정의역
정의역이란, 확률 변수가 가질 수 있는 집합이다.
- 윳놏이에서는 [도, 개, 걸, 윷, 모]가 정의역이다.
Probability distribution(확률분포)
확률분포란, 정의역 전체에 걸쳐 확률을 표현한 것이다.
- 또는 라고 표기한다.
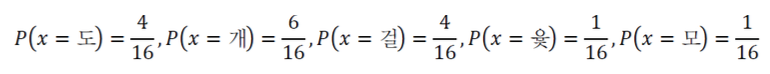
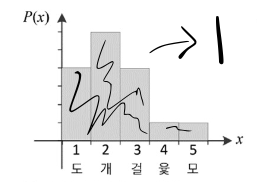
Probability mass function(확률질량함수)
확률질량함수는 정의역이 이산값을 가지는 확률분포를 의미한다.
확률은 항상 0 이상이며, 정의역에 걸쳐 확률을 더하면 1이 돼야 한다.
- ex) 윷놀이
Probability density function(확률밀도함수)
확률밀도함수는 정의역이 연속적인 값을 가지는 확률분포를 의미한다.
확률은 항상 0 이상이며, 정의역에 걸쳐 확률을 더하면 1이 돼야 한다.
- ex) 키, 몸무게
Random Vector(확률 벡터)
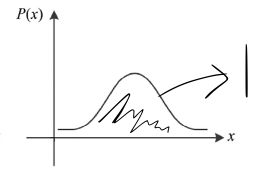
확률 벡터란, 확률변수가 vector인 경우를 의미한다.
- Iris data는 샘플이 4개의 특징값으로 표현되므로, 확률 변수는 4차원 벡터여야 한다.
➡️ 정의역이 4차원 실수 공간인 이 된다.
곱 규칙과 합 규칙
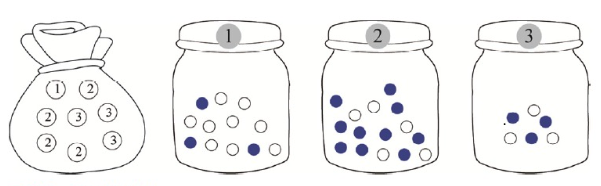
1. 주머니에서 카드 1장을 꺼내, 해당하는 병에서 공을 꺼낸다
2. 꺼낸 카드와 공은 다시 제자리에 놓는다.
3. ,
4. 정의역 : {1, 2, 3}, {B, W}
위 규칙을 따라, 여러가지 확률을 계산해보자.
조건부 확률
조건부 확률이란, 사건 B가 이미 발생한 조건에서 사건 A가 발생할 확률을 의미한다.
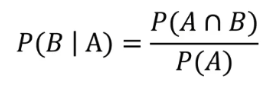
곱 규칙 & join probability(결합 확률)
곱 규칙은 다음과 같다.
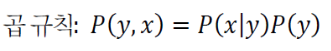
결합 확률이란, 두 사건이 결합된 상태의 확률을 의미한다.
- ex) 카드는 1번이고, 공은 W일 확률은 로 표기한다.
- 결합 확률 계산 방법 : 곱 규칙(ft. 조건부 확률)

합 규칙
-
이제 하얀 공(W)이 뽑히 확률 P(W)을 생각하자.
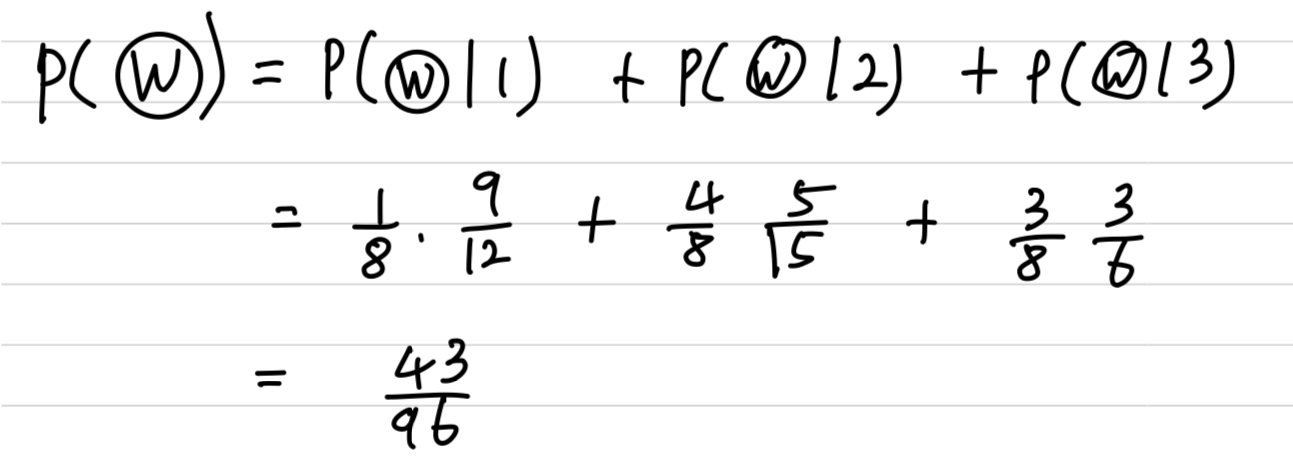
-
위와 같은 계산식을 합 규칙이라고 한다.
합 규칙의 일반적인 형태 :
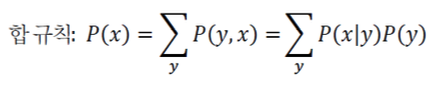
독립(independent)
-
두 확률변수가 다음의 식을 만족하면, 둘은
독립이라고 말한다.
-
위의 카드, 공 예제는 카드에 따라 공이 결정되기 때문에 서로 연관성이 있다는 것을 직관적으로 알 수 있다.
그렇기 때문에 두 확률변수는 서로 독립이 아니라는 사실도 알 수 있다.
베이즈 정리와 기계 학습
Bayes Formula(베이즈 정리)
-
일반적으로
와 가 같이 일어난 결합확률이나
와 가 같이 일어난 결합확률이 같으므로 다음과 같은 식이 성립된다.
-
위의 식을 정리하면,
베이즈 정리가 된다.
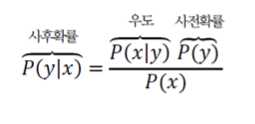
베이즈 정리를 확률 실험에 적용하면, 다음 질문에 대한 합리적인 답을 구할 수 있다.
"하얀 공(W)이 나왔다는 사실만 알고 어느 병에서 나왔는지 모르는데, 어느 병인지 추정하라"
-
을 계산하여
가장 큰 값을 가진 병 번호를 선택하면 된다.
➡️
➡️ -
위의 식을 계산하여 3번 병일 확률이 가장 높다는 합리적인 답을 구할 수 있다.
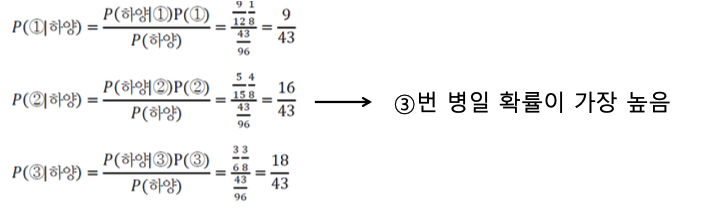
베이즈 정리의 의미
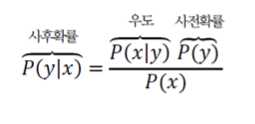
- 사후확률 : 사건 발생 후의 확률
- 사전확률 : 사건 와 무관하게 알 수 있는 확률
- 우도(likelihood)
likelihood(우도)
-
보통 조건부 확률을
|의 오른쪽에 이미 알고 있는 사건을 쓰고,
|의 왼쪽에 추정해야 할 사건을 쓴다. -
하지만
우도는 위치가 뒤바뀐다.
|의 오른쪽에 추정해야 할 사건을 쓰고,
|의 왼쪽에 이미 알고 있는 사건을 쓴다.
- 우도는 다음과 같이 기호를 사용한다.
우도 : P =
: 추정해야 할 사건
: 이미 알고 있는 사건
기계학습에 확률 이론 적용
- Iris 데이터 Classification 문제에 사후확률 추정
: 특징 벡터(4차원)이므로 확률 벡터로 표기
: Classification 결과 == 부류

➡️(=사후확률)을직접 추정하는 것은 아주 단순한 상황을 빼고는불가능하다.
Iris data는 가 만드는 공간이 4개이지만,
다른 datae들은 대부분 무수히 많은 점을 가지므로,
이 모든 점에 대해 확률을 일일이 표현할 수 없기 때문이다.
따라서
1. 사전확률 P(y)와
2. 우도 P(x|y)
를 구할 수 있다면, 베이즈 공식을 이용하여사후확률을 간접적으로 계산할 수 있다.
그렇다면 우도(P(x|y))는 사후확률(P(y|x))보다 구하기 쉬운가?
➡️ 우도에서는 부류 y가 고정된 셈이어서 다른 부류의 샘플을 모두 배제한 채 y에 속하는 샘플만 가지고 확률 분포를 추정하면 되므로 추정이 훨씬 쉽다.
➡️ 다시 말해, 부류별로 독립적으로 확률을 추정할 수 있다.
1. 사전확률 추정
무작위로 개의 Iris를 채집하였는데,
그 중 setosa, versicolor, virginica가 각각 , , 개라면
사전확률 P(y)는 다음과 같이 구할 수 있다.
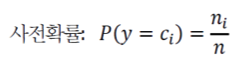
2. 확률밀도 추정 방법을 이용한 우도 추정 방법
우도 추정에 적용할 수 있는 여러 가지 확률밀도 추정(density estimation)방법이 있다.
- 파젠 창 방법 : 어떤 점에 일정한 크기의 마스크를 씌우고 점 속으로 들어오는 샘플의 개수를 세어 확률을 추정하는 방법
- 가우시안과 같은 매개변수화된 확률분포함수를 가정하고 매개변수를 추정하는 방법
- 가우시안을 여러 개 혼합하여 정확도를 높이는 방법.
- 등등 여러가지 추정 방법이 있다.
이에 대한 자세한 내용은 Chapter 6.4(나중에 Link 달기) 참고
최대 우도
이제 다음의 그림처럼 일부 또는 전부가 가려진 상황에서
가려진 곳에 있는 매개변수를 추정하는, 더 복잡한 문제를 생각해 보자.
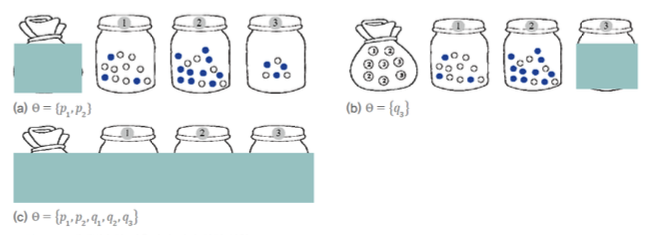
-
(a) : 카드를 담은 주머니가 가려져 있어 카드 1, 2, 3의 확률을 추정해야 한다.
세 확률을 더하면 1이 돼야 하므로,
카드 1, 2의 확률 , 만 추정하면 된다. -
(b) : 3번 병에 들어있는 B의 확률 를 추정하면 된다.
W의 확률은 1-으로 구할 수 있다. -
(c) : 전체가 가려져 있어 추정해야 하는 매개변수가 5개나 된다.
편의상 주머니와 관련된 확률은 , 병과 관련된 확률은 로 표기하여
매개변수의 집합은 = {, , , , }로 표기.
최대 우도법
실험을 여러 번 반복하여 공의 색깔, 즉 데이터집합 를 다음과 같이 얻었다고 가정하자.

(b)의 경우, 3번 병만 가려진 상황에서 매개변수 를 추정하는 문제가 주어졌다.
이때 추정해야 하는 것은 B의 확률 이고, W는 로 구할 수 있으므로
매개변수는 2개가 아니라 1개이다.
따라서 문제를 다음과 같이 정의할 수 있다.
" 데이터 X가 주어졌을 때,
X를 발생시켰을 가능성을 최대로 하는 매개변수 의 값을 찾아라. "
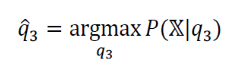
이 식을 우도를 최대화하는 해를 구한다는 뜻에서
최대 우도 추정(MLE, Maximum Likelihood Estimation)이라고 한다.
최대 우도법을 일반화하면 다음과 같다.
수치 문제를 피하기 위해 log 표현으로 바꾸면 다음과 같다.
딥러닝에서 최대 우도법 활용
관찰 결과는 훈련집합 = {}이고,
추정해야 할 매개변수는 신경망의 가중치집합 이다.
- 예를 들어, 0~9까지 숫자 인식용 신경망이 있다고 가정하자.
크기의 비트맵을 입력받은 숫자 인식용 신경망이
784-100-100-100-10의 구조를 가진다면
는 개의 매개변수로 구성된다.
➡️ 얼핏 이렇게 많은 매개변수의 최적 조합을 찾아내는 일이 불가능해 보이지만,
여러 기법이 협력하여, 그 중 목적함수와 최적화 알고리즘이 핵심 역할을 하여 복잡한 문제를 거뜬히 풀어낸다.
평균과 분산
Mean(평균)
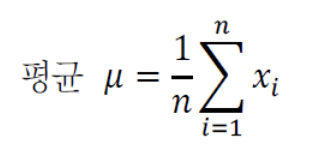
Variance(분산)
-
Variance()는 평균을 기준으로 데이터가 얼마나 퍼져있는지를 측정하는 수치이다.
Variance ⬇️ : 평균에 모여있다
Variance ⬆️ : 골고루 분포한다 -
분모를 m-1로 나누는 이유는 자유도(주어진 데이터에서 계산 가능한 독립적인 정보의 개수)와 관련이 있다.
m-1로 나누면 자유도를 고려하여 모집단의 분산을 더 정확하게 추정할 수 있기 때문이다.
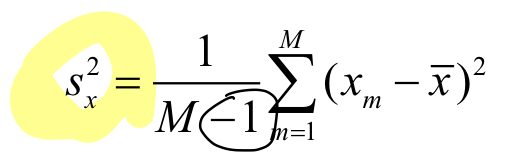
Standard Deviation(표준편차)
Standard Deviation()은 Variance의 제곱근이다.
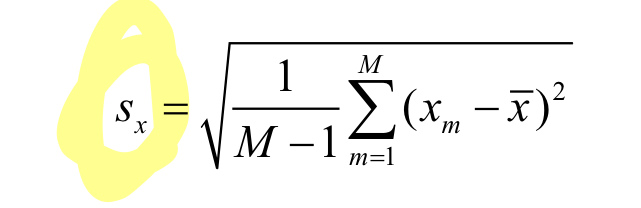
Covariance(공분산)
-
A = [M * N] Matrix라고 가정.
A의 Covariance()는 [N * N]이 된다. (Column 개수 * Column 개수)
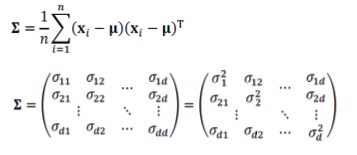
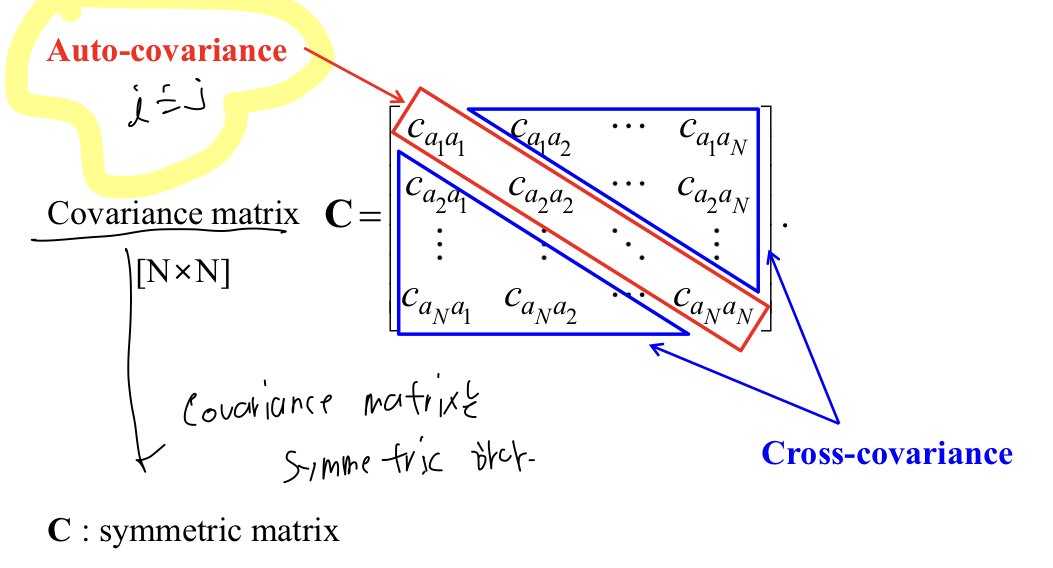
-
example

-
Covariance는 symmetric Matrix이다.
확률분포
확률분포란, 확률 변수(random variable)의 가능한 모든 값들과 그 값들이 나타날 확률을 나타내는 함수.
기계 학습에서 널리 사용하는 확률분포
1, 가우시안 분포
2. 베르누이 분포
3. 이항 분포
이 분포들은 모양이 일정한데, 1개 또는 2개의 매개변수로 모양을 조절할 수 있다.
1. 가우시안 분포 == 정규분포
가우시안 분포(Gaussian Distribution) == 정규분포(Normal Distribution)
-
특징벡터가 1차원인 가우시안 분포
평균과 분산을 나타내는 2개의 매개변수 와 로 규정하며,
와 같이 표기한다. 확률변수를 생략하여 로 표기하기도 한다.
; 앞에 ➡️ 확률변수
; 뒤에 ➡️ 매개변수
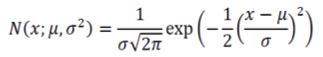
- (평균) : 최대값을 가지는 지점
(분산) : 분포의 퍼진 정도.
➡️ 클수록 봉우리의 높이가 낮고 좌우로 멀리 퍼짐.
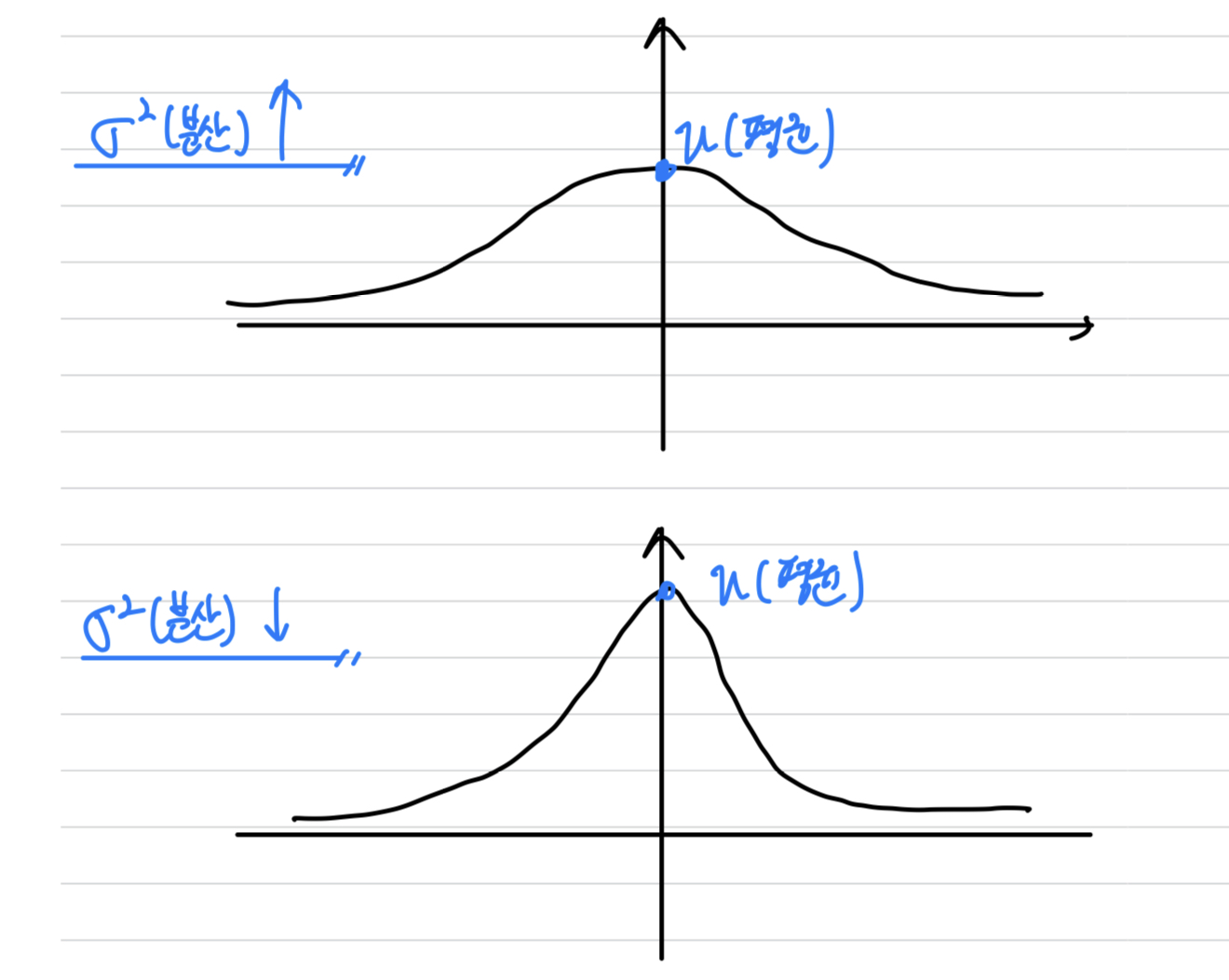
- (평균) : 최대값을 가지는 지점
-
특징벡터가 다차원인 가우시안 분포
평균 벡터과 공분산 행렬을 나타내는 2개의 매개변수 와 로 규정하며,
와 같이 표기한다. 확률변수를 생략하여 로 표기하기도 한다.
; 앞에 ➡️ 확률변수
; 뒤에 ➡️ 매개변수
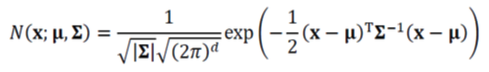
- (평균) : 최대값을 가지는 지점
(공분산) : 분포의 퍼진 정도.
➡️ 클수록 봉우리의 높이가 낮고 좌우로 멀리 퍼짐.
: det() == 공분산의 행렬식.
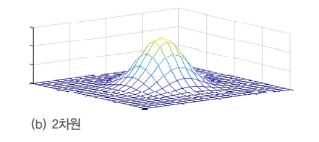
- (평균) : 최대값을 가지는 지점
2. 베르누이 분포
확률변수 가 1(성공) 또는 0(실패)의 두 가지 값만 가질 수 있는 이진변수이고,
성공확률 : , 실패확률 : 인 분포를 베르누이 분포(Bernoulli Distribution)라고 한다.
매개변수는 하나이다.

이항 분포
- 성공확률이 인 베르누이 실험을 번 수행할 때,
성공할 횟수의 확률분포를이항 분포(Binomial Distribution)라고 한다.
매개변수는 두 개이다. (베르누이 분포는 이항 분포에서 m=1인 특수 형태)
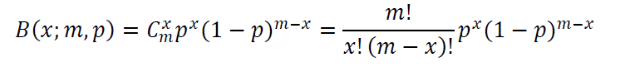
- : Combination, 서로 다른 개 중에서 개를 뽑는 가지 수
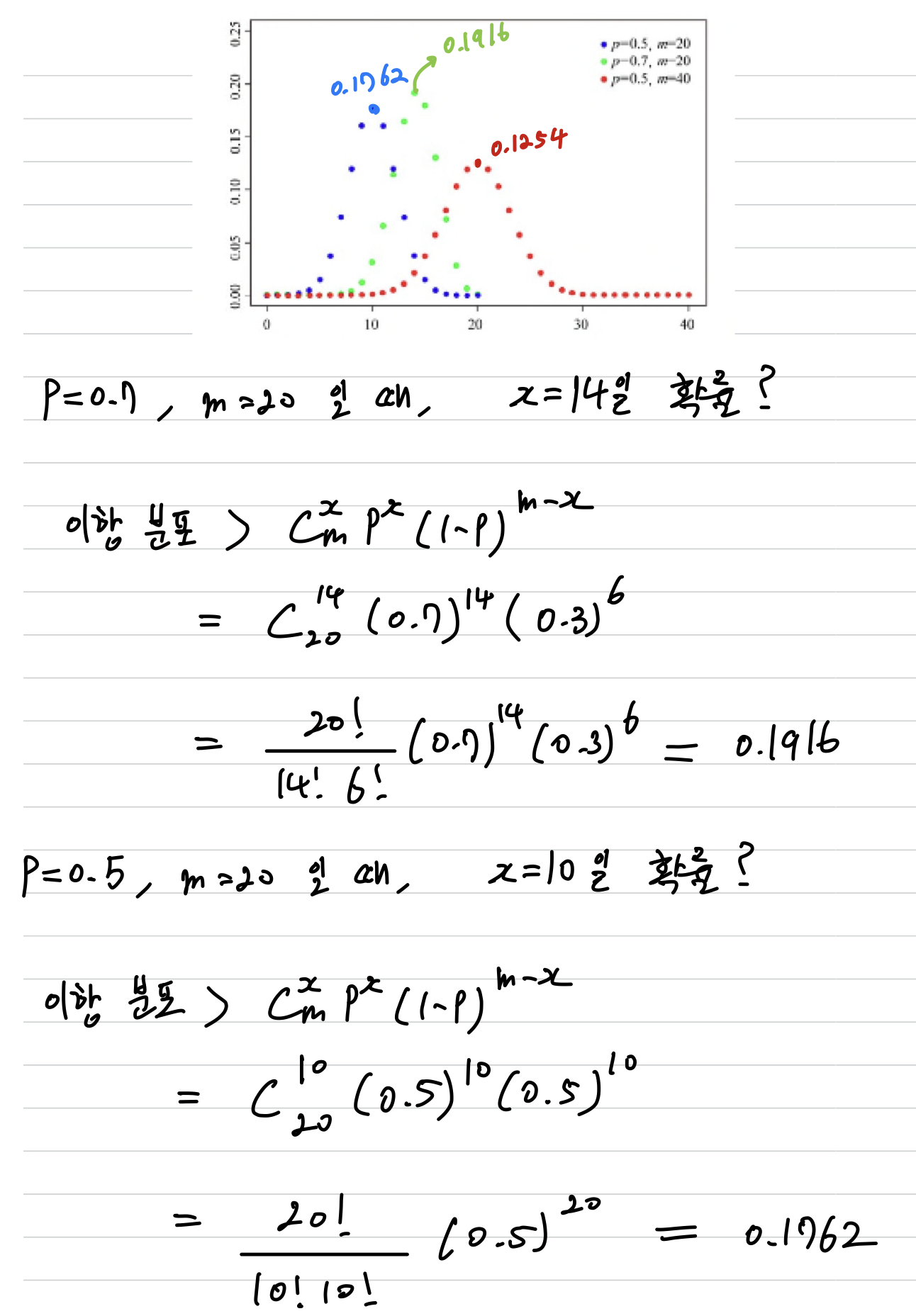
- : Combination, 서로 다른 개 중에서 개를 뽑는 가지 수
베르누이 분포는 =1일 때의 이항 분포로서,
베르누이 분포는 이항 분포의 특수한 형태임을 알 수 있다.
차이점 : 가우시안 분포 vs 이항 분포
- 정리하자면,
- 대상 :
가우시안 분포는 연속적인 데이터를 모델링.
이항 분포는 이진적 결과를 갖는 데이터를 모데링. - 매개변수 :
가우시안 분포는 평균()과 분산()라는 2개의 매개변수를 가짐.
(다차원의 경우 평균벡터()와 공분산행렬())라는 2개의 매개변수를 가짐.
이항 분포는 시행횟수()과 성공확률()라는 2개의 매개변수를 가짐. - 모양 :
가우시안 분포는 평균값을 중심으로 좌우 대칭의 그래프.
이항 분포는 왼쪽이나 오른쪽으로 치우친 분포를 가질 수 있음.
- 대상 :
정보이론
정보이론(Information Theory)에서는 메시지(=사건)의 정보량을 확률로 측정한다.
확률이 낮은 사건일수록 더 많은 정보를 전달한다.
ex. 윷놀이에서 "개가 나왔다." 보다는 "모가 나왔다"라는 메시지를 들으면 "놀라운 뉴스네."라는 반응을 보인다.
자기 정보(self-information)
자기 정보(self-information)란,
특정 사건 이 일어날 확률을 추정할 수 있다면, 그 특정 사건의 정보량을 의미한다.
확률변수를 라 하고 의 정의역을 {}라고 하자.
정보이론에서 사건 의 자기 정보량 를 측정해보자.
-
정보이론에서
자기 정보정보량을 계산하기 위해 다음의 식을 이용한다.

-
예상 가능한 사건에 대한 정보는 자기 정보량이 작다.
- ex) 윷놀이에서 모와 개가 나온 사건의 자기 정보는 다음과 같다.

- ex) 윷놀이에서 모와 개가 나온 사건의 자기 정보는 다음과 같다.
단위 : bit, nat
bit(비트) : 확률이 1/2(==0.5)일 때, 1bit의 정보량을 갖는다.
nat(나츠) : 확률이 1/e(==0.3679)일 때, 1nat의 정보량을 갖는다.
엔트로피(Entropy)
엔트로피(Entropy)란,
확률분포의 무질서도 또는 불확실성(Uncertainty)를 측정한다.
-
이산 확률분포의 엔트로피는 다음과 같이 정의한다.
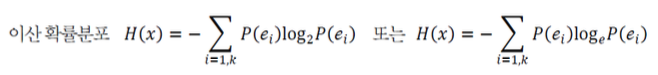
-
연속 확률분포의 엔트로피는 다음과 같이 정의한다.
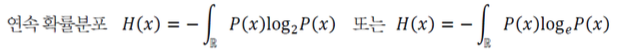
-
모든 사건이 동일한 확률을 가질 때, 엔트로피가 최대이다.
➡️ 예측하기 어려워서 더욱 무질서하고 불확실성이 크기 때문- ex) 윷 vs 주사위 엔트로피

- ex) 윷 vs 주사위 엔트로피
Cross Entropy와 KL Divergence
엔트로피는 하나의 확률분포의 무질서 정도를 측정한다.
그런데 교차 엔트로피(Cross Entropy)는 두 확률분포 간의 엔트로피를 측정한다.
- 서로 다른 두 확률분포 와 사이의 교차 엔트로피는 다음과 같이 정의한다.
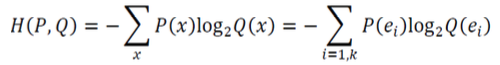
KL Divergence
-
Cross Entropy의 식을 통해서
KL divergence(다이버전스)를 유도할 수 있다.

➡️ (와 의 교차 엔트로피) = (의 엔트로피) + (와 의 KL 다이버전스) -
KL divergence는
두 확률분포가 서로 얼마나 다른지를 측정한다.
➡️두 확률분포 사이의 거리를 계산할 때 주로 사용한다.
(엄밀한 수학적 정의에 따르면 != 이므로 거리가 아니지만)
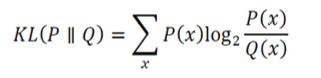
example (Cross Entropy, KL divergence)

cost function으로서의 Cross Entropy
- 목적함수로 평균제곱 오차(MSE)는 직관적으로 가장 이해하기 쉽고 널리 사용된 함수지만,
기계 학습 과정에서 더 큰 오류에 더 낮은 벌점을 주는 경우가 발생하는 한계를 노출하기도 한다.
그래서 딥러닝에서는 교차 엔트로피를 MSE의 대안으로 즐겨 사용한다.
나중에 5.1절에서 교차 엔트로피 목적함수의 원리와 장점 등을 공부한다.