신경망 기초
Artificial Neural Network & Biological Neural Network
-
Neuron: 사람의 뇌 속에 있는, 가장 작은 정보처리 단위로서 세포체, 수상돌기, 축삭으로 구성된다.- 세포체 : 간단한 연산을 담당한다
- 수상돌기 : 다른 Neuron으로부터 신호를 받는다
- 축삭 : 처리 결과를 다른 Neuron에게 전달한다
-
Biological Neural Network(생물 신경망):
Neuron은 망을 형성하므로 Neuron의 집합을 Biological Neural Network라고 한다. -
Aritificial Neural Network(인공 신경망):
Biological Neural Network를 공학적으로 접근하여 인공적으로 모방한 모델.
신경망의 종류
-
Feedforward Neural Network&Recurrent Neural Network-
Feedforward Neural Network(전방 신경망):
모든 계산이 왼쪽에서 오른쪽으로 진행된다.
DMLP(Deep Multi Layer Perceptron)과 CNN(Convolution Neural Network)이 Feedforward Neural Network에 속한다.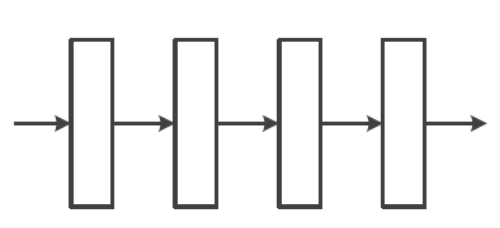
-
Recurrent Neural Network (순환 신경망):
오른쪽에서 왼쪽으로 진행하는 Feedback 계산도 포함된다.
RNN(순환 신경망)과 LSTM이 Recurrent Neural Network에 속한다.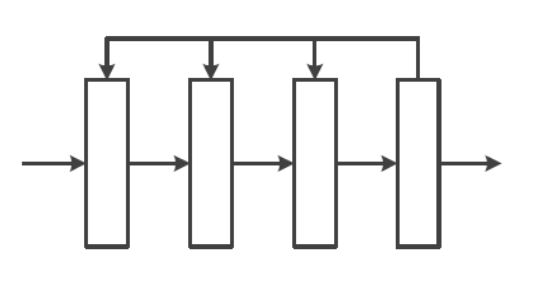
-
-
Shallow Neural Network&Deep Neural Network-
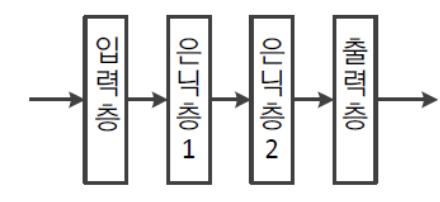
Shallow Neural Network:
은닉층이 1~2개 정도인 Neural Network를 Shallow Neural Network라고 한다.
-
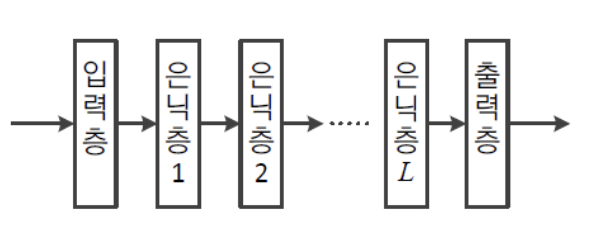
Deep Neural Network:
은닉층을 많이 가진 Neural Network을 Deep Neural Network라고 한다.
-
-
Deterministic Neural Network&Stochastic Neural NetworkDeterministic Neural Network:
입력이 같으면 항상 같은 출력이 나온다. 계산식의 임의성이 없기 때문이다.Stochastic Neural Network:
계산식이 확률에 따른 난수를 사용하므로 입력이 같아도 매번 다른 출력이 나온다.
Chapter 10에서 다룰 RBM과 DBN은 대표적인 Stochastic Neural Network이다.
Stochastic Neural Network는 Classification과 Regression과 같은 예측뿐 아니라 유사한 패턴을 생성하는 능력을 부여하면 생성 모델로 활용할 수 있다.
퍼셉트론
- Perceptron은 학습이 가능한 초창기 Neural Network 모델이다.
- 딥러닝을 포함하여 현대 Neural Network는 Perceptron의 병렬 구조와 순차 구조로 결합한 형태이다.
즉, Perceptron은 현대 Neural Network의 중요한 구성 요소이다.
구조와 동작

구조입력층과출력층이 존재.
(입력층은 아무런 연산을 하지 않으므로 층의 개수를 셀 때 제외.
따라서 perceptron은 1개의 층이 있다고 말한다.)- 입력층에 있는 입력 node는
Feature Vector의 Feature 하나에 해당. - 입력층에는
bias라고 하는 node도 존재. edge는 입력 node와 출력 node를 연결한다.- edge마다
weight를 갖는다.
동작- Feature Vector 를 input으로 준다.
- 서로 연결된 feature value와 weight를 곱한 결과를 모두 더한다.
이렇게 구한 값 를 Activation Function(Step Function)에 넣어 최종 결과를 출력한다.
행렬 표기

Example(OR Gate)
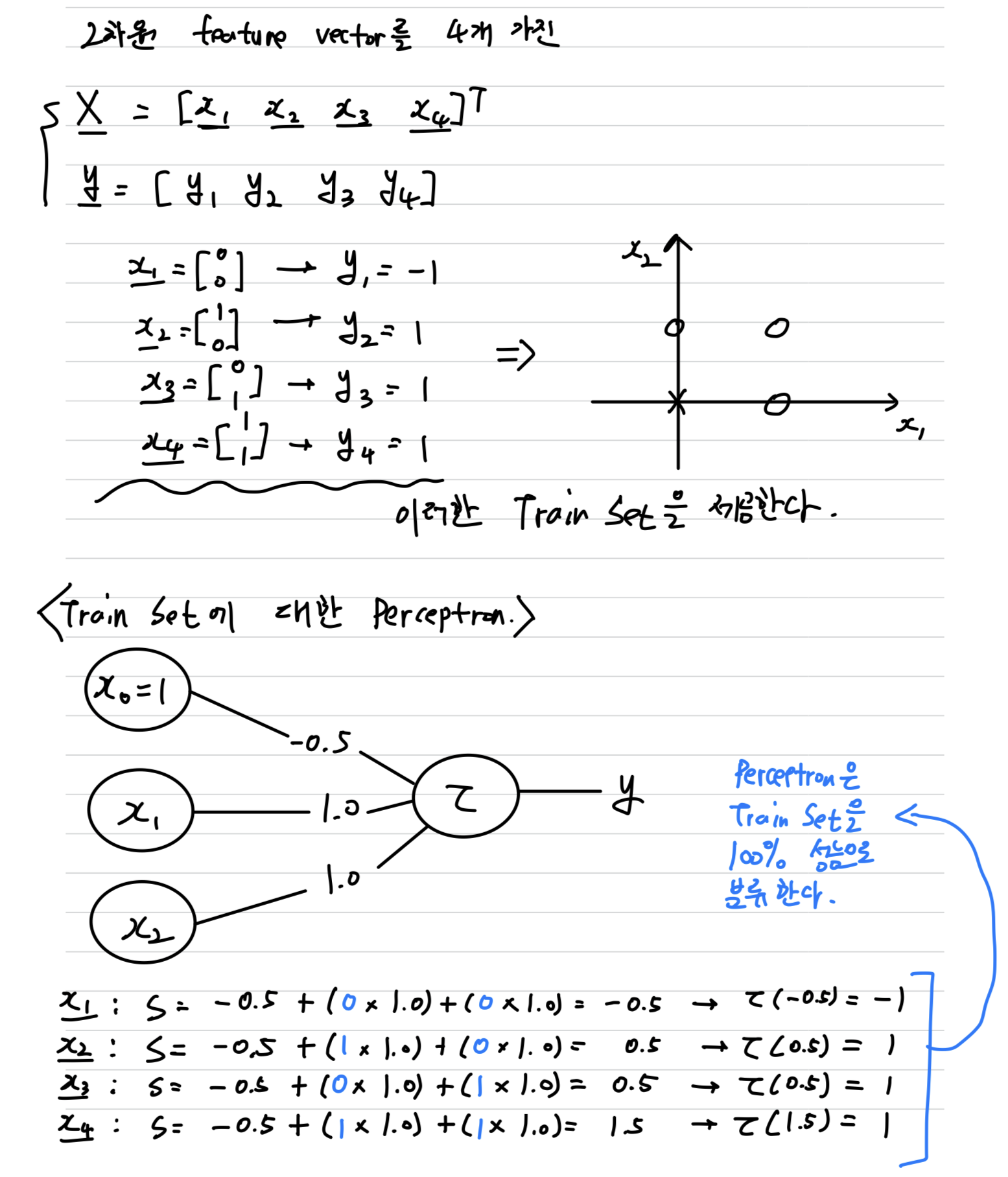
- Train Set의 X를 100% 분류하는 Perceptron은 무수히 많다.
예를 들어 node에 연결된 weight를 0.9로 바꾸어도 성능은 100%이다.
Perceptron은 Linear Classifier이다.
-
위의 예제를 기하학적으로 나타내면 다음과 같다.
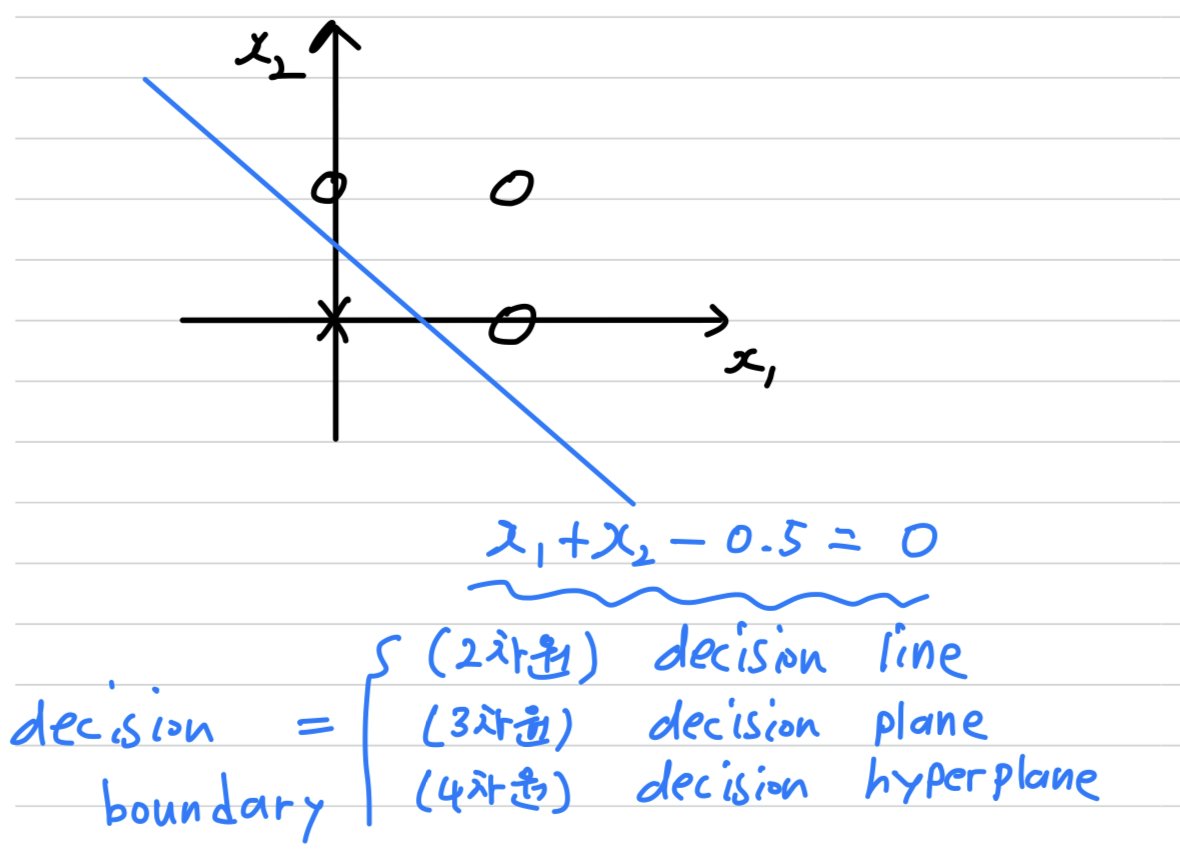
- OR gate 예제에서 Preptron은 이진 분류기로 작용한다.
-
2차원에서 특징 공간을 나눔으로써 Classification을 결정하는 경계선을
Decision Line이라고 한다.
은 직선의 방향, 은 절편을 결정하여 다음과 같은 직선의 방정식을 구할 수 있다.
➡️ -
3차원에서 특징 공간을 나눔으로써 Classification을 결정하는 경계면을
Decision Plane이라고 한다.
은 직선의 방향, 은 절편을 결정하여 다음과 같은 평면의 방정식을 구할 수 있다.
➡️ -
4차원 이상에서 특징 공간을 나눔으로써 Classification을 결정하는 경계를
Decision Hyperplane이라고 한다.
은 직선의 방향, 은 절편을 결정하여 다음과 같은
방정식을 구할 수 있다.
➡️ -
Decision Line, Decision Plane, Decision Hyperplane처럼 특징 공간을 나누며 Classification을 결정하는 경계를
Decision Boundary라고 한다.
학습
-
앞에서는 학습이 이미 다 되어 있는 Perceptron에 대해서 Test한 셈이다.
이제는 Train Set으로 Perceptron을 어떻게 학습시키는지 살펴보자.
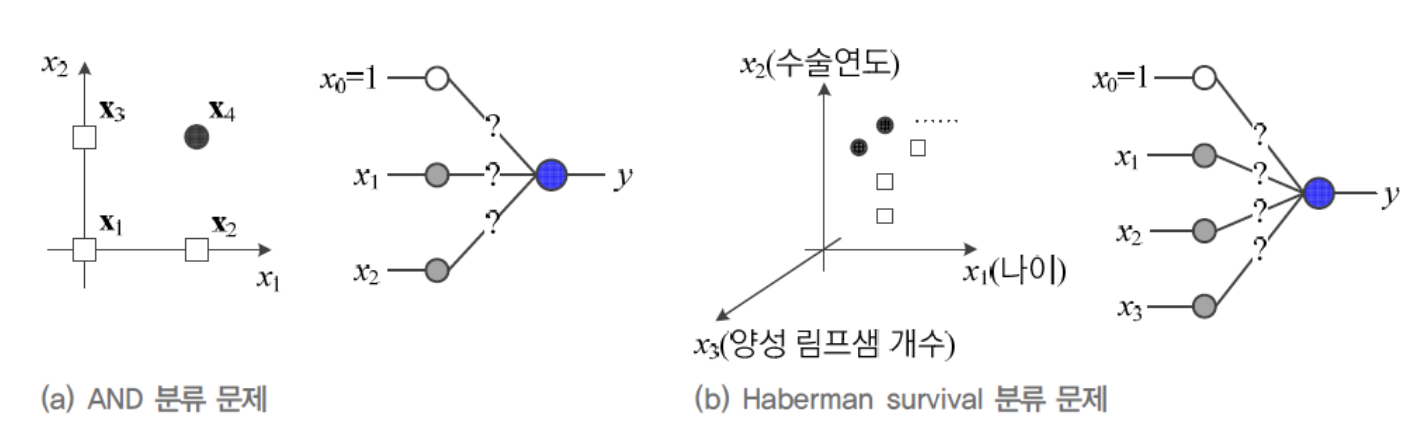
OR Classification 문제를 AND Classification 문제로 바꿔서
가 어떤 값을 가져야 4개의 Sample을 제대로 분류할 수 있을까? -
Haberman Survival Classification 문제는 간단한 데이터 축에 속하는데,
feature vector가 3차원이고, Sample이 306개나 되어,
사람이 weight 매개변수값을 찾는 것은 매우 어렵다.
따라서 자동으로 최적의 매개변수값(weight)을 찾아주는 학습 알고리즘에 대해서 공부할 것이다.
목적함수와 delta rule 유도
목적함수 유도
- 기계 학습이 추정해야 할 매개변수 집합을 로 표기한다.
- Perceptron에서 는 weight()라고 볼 수 있다.
- 따라서 목적함수를 로 쓸 수 있다.
- 목적함수는 다음과 같은 조건을 만족해야 한다.
- 이다.
- 가 최적이면, 즉 모든 Sample을 맞히면 이다.
- 틀리는 Sample이 많은 일수록, 는 큰 값을 가진다.
- 위의 3가지 조건을 만족하는 식은 다음과 같다. (는 가 틀리는 Sample의 집합이다.)
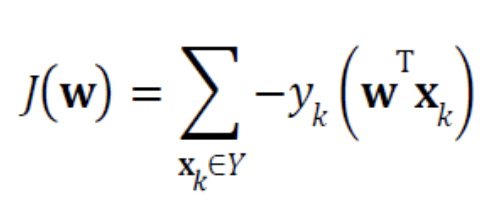
- 는 가 를 잘못 예측한 값인 다.
따라서 와 는 서로 부호가 반대이다.
따라서 는 항상 양수이다.
따라서 결국 가 클수록, 즉 틀린 Sample이 많을 수록 는 큰 값을 가지게 되고,
가 공집합일 때, 이 된다.
- 는 가 를 잘못 예측한 값인 다.
delta rule 유도
- 이제 가중치 갱신 규칙 를 적용하면 된다.
- 는 의 gradient이므로 를 로 편미분한다.
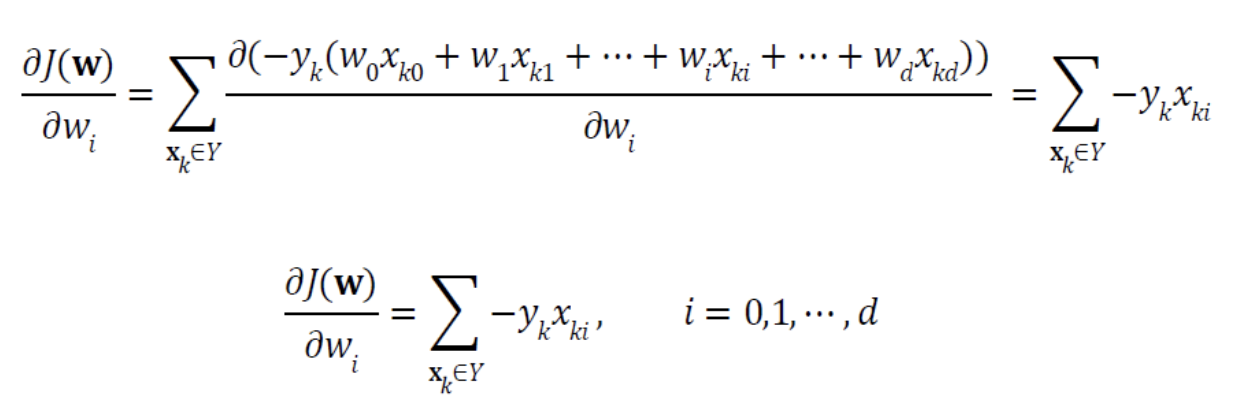
- 를 에 대입하면,
Perceptron의 학습 규칙으로서delta rule이 나온다.
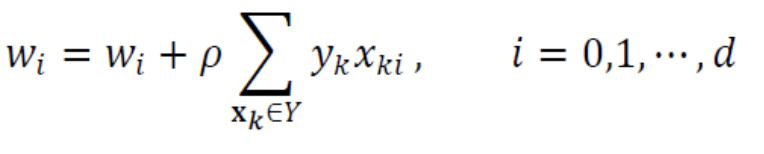
delta rule 행렬 표기
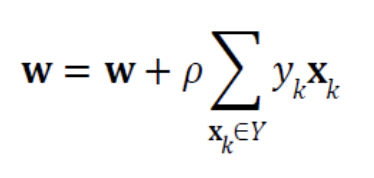
학습 알고리즘 (batch or stochastic)
batch 버전
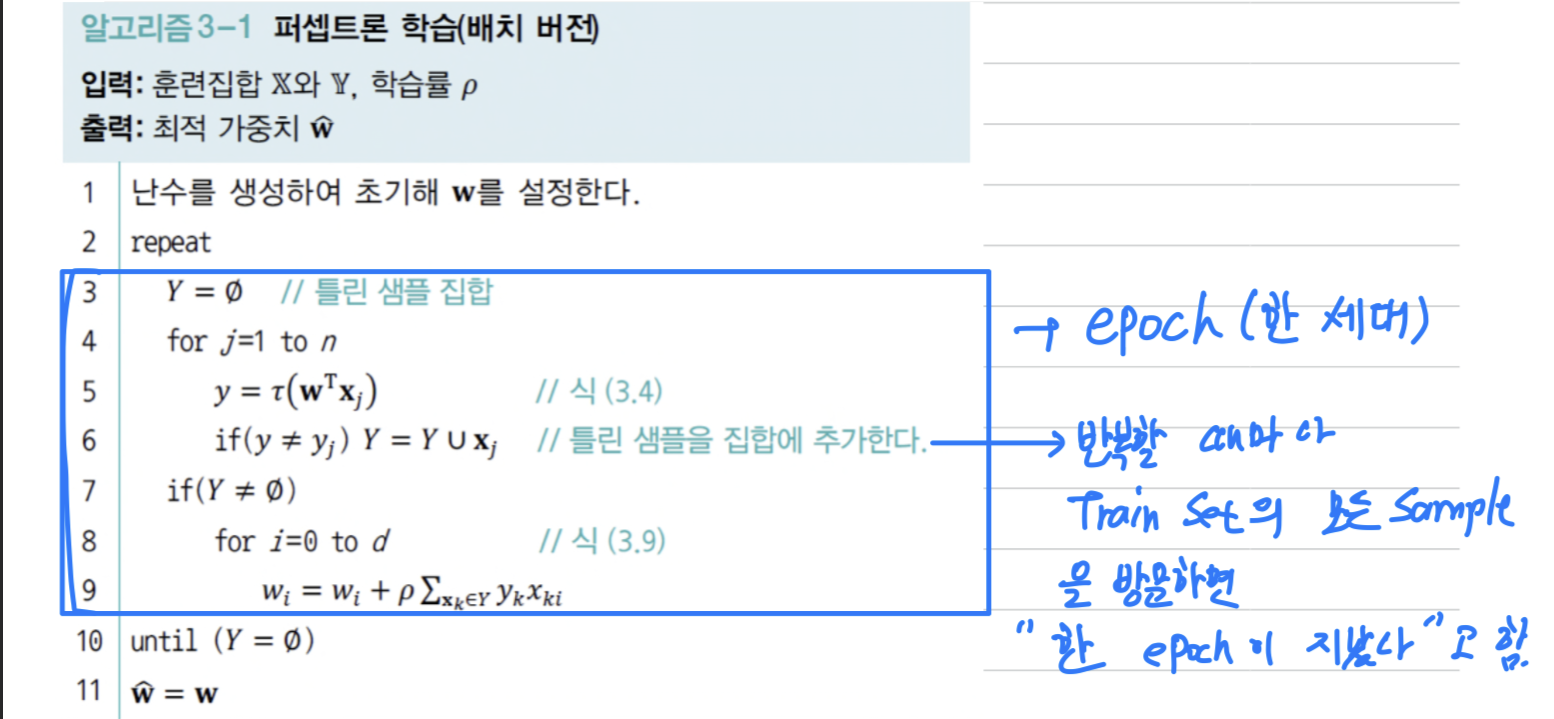
- 반복할 때마다 Train Set의 모든 Sample을 방문한다.
이를 "한 epoch(세대)가 지났다"라고 한다.
Stochastic 버전 (== Online 버전)

- 틀린 Sample이 발생하는 즉시 매개변수를 갱신한다.
또한 Sample의 순서를 랜덤으로 섞는다(Shuffle).
이러한 연산 때문에 "Stochastic"이라는 단어가 붙는다.
현대 기계 학습은 Batch version보다 Stochastic version을 채택한다.
Stochastic version의 성능이 더 좋다고 입증되었다.
(사실은 추후에 공부할 mini batch stochastic...)
다층 퍼셉트론
-
Perceptron의 동작은 다음과 같이 규정되므로 Linearly Separable한 상황밖에 처리하지 못한다.
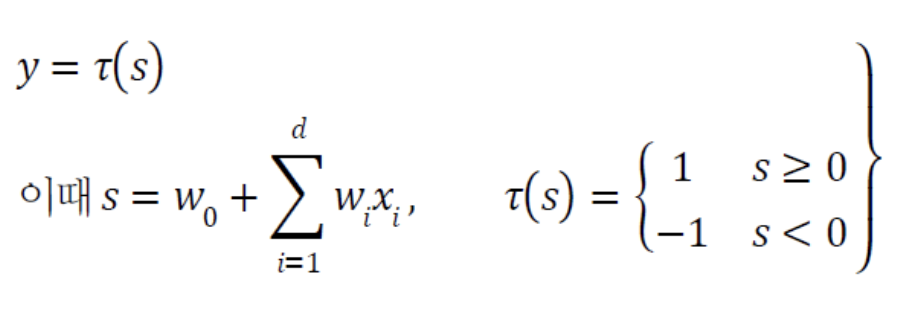
-
따라서 다음의 (b)와 같이 Linearly Non-separable한 상황은 일정한 양의 오류를 범할 수 밖에 없다.
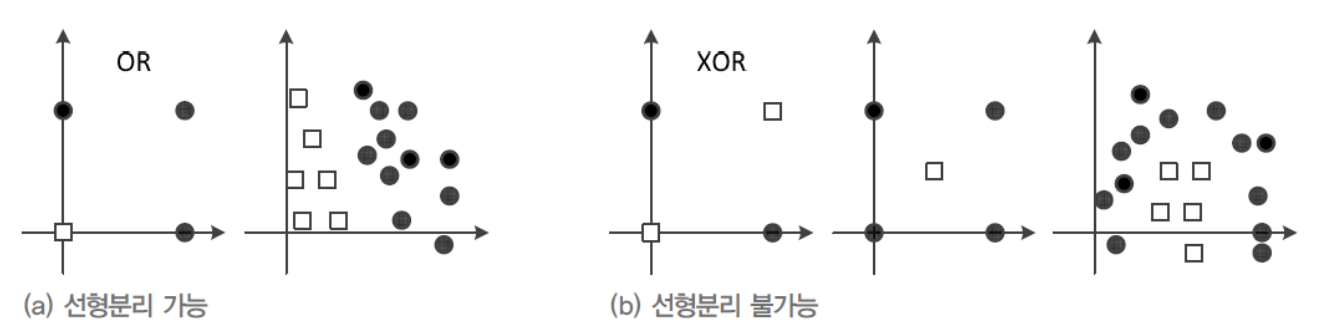
- XOR Classification 문제는
어떤 Decision Line을 사용하든지 Sample 하나는 틀리게 되므로
Perceptron은 최대 75% 정확률이라는 한계가 있다.
- XOR Classification 문제는
-
Multi-layer Perceptron(MLP, 다층 퍼셉트론)은
여러 개의 Perceptron을 결합한 다층 구조를 이용하여
위의 예시와 같이 Linear non-separable한 상황을 해결할 수 있다.
MLP의 핵심 아이디어
은닉층을 둔다.
은닉층은 원래 특징 공간을 분류하는 데 훨씬 유리한새로운 특징 공간으로 변환한다.Sigmoid Activation Function을 도입한다.
Activiation Function에 Step Function으로 두면, Hard 의사결정에 해당한다.
반면 Sigmoid로 두면,Soft 의사결정이 가능하다.
Soft 의사결정에서는 출력이 연속값인데, 출력을 신뢰도로 간주함으로써융통성 있는 의사결정을 할 수 있다.Back Propagation(오류 역전파)알고리즘을 사용한다.
Multi Layer를 역방향으로 진행하면서 한 번에 한 층씩 Gradient를 계산하고 가중치를 갱신하는 방식이다.
위의 핵심 아이디어와 함께 모멘텀, 적응적 합습률, 미니배치, 규제와 같은 요령을 적용한다. (Chapter 5에서..)
특징 공간 변환
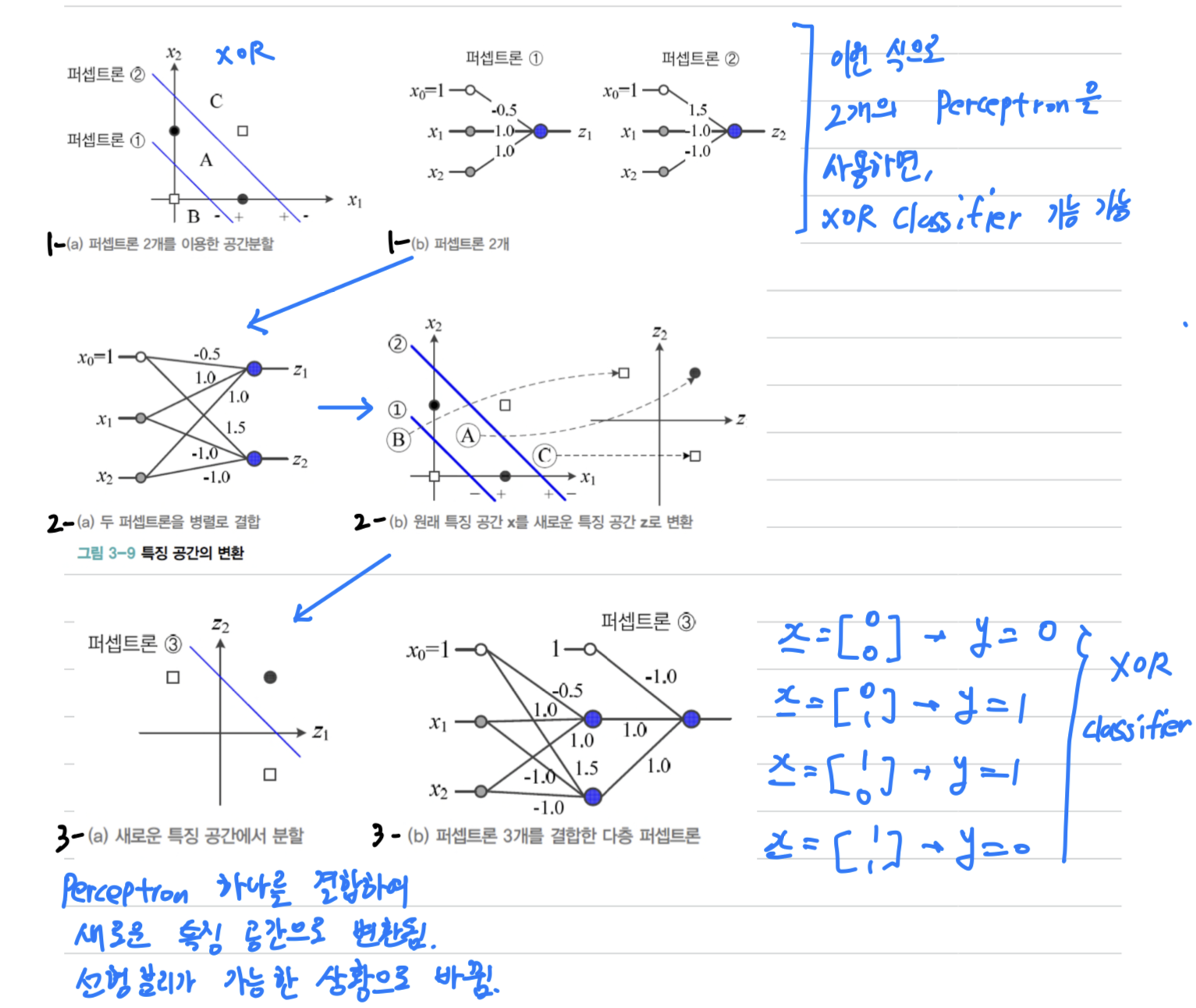
-
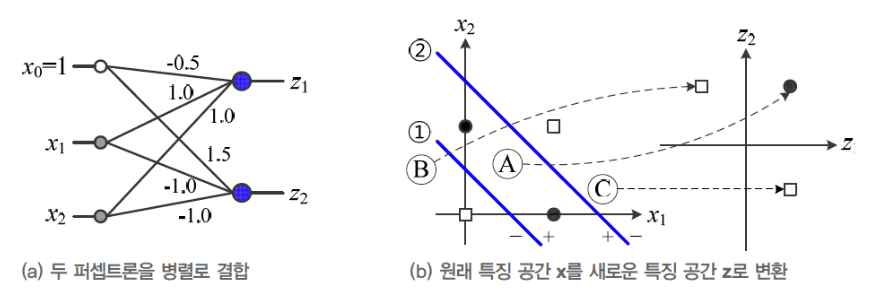
1-(a)를 보면, Decision Line 2개로 XOR Classifier 문제를 해결할 수 있음을 알 수 있다. -
1-(a)의 Decision Line을 결정하기 위한 각각의 Perceptron은1-(b)와 같이 만들 수 있다. -
1-(b)를 병렬 결합하여2-(a)의 Perceptron으로 만들 수 있다. -
2-(a)Perceptron에 대해서 특징 공간 를 그리면,
2-(b)와 같이 새로운 특징 공간 로 변환된다. -
3-(a)의 - (파란 실선)은 새로운 특징 공간 를 Classification하는 세 번째 Perceptron이다.
(새로운 특징 공간 는 Linearly separable한 상황이 된다) -
3-(a)의 세번째 Perceptron을 결합한 최종 MLP는3-(b)와 같다. -
3-(b)는 XOR Classification을 구현하는 MLP가 된다.
MLP의 용량
-
위의 예제에서, feature vector가 2차원인 input에 대해
Perceptron을 2개 사용하여 2차원 공간으로 변환되었다.
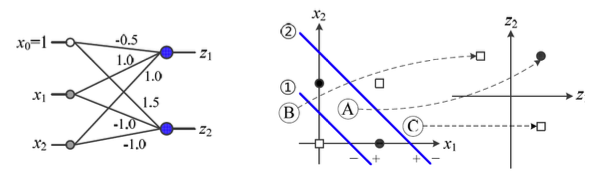
-
아래 예제에서, feature. vector가 2차원인 input에 대해
Perceptron을 3개 사용하여 3차원 공간으로 변환되었다.
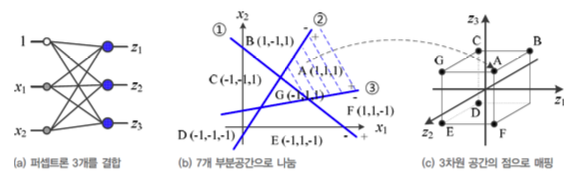
일반화하면
원래 Feature Vector가 2차원이고 Perceptron을 p개 결합한 상황에서,
이때 신경망은 2차원 공간을 p차원 공간으로 변환한다.
또한 p개의 직선은 개의 공간을 나눌 수 있다
따라서 p가 클수록 신경망의 용량이 크다.
하지만 용량이 너무 크게 되면(Perceptron이 너무 많게 되면),
Overfitting될 가능성이 커지므로 무턱대고 크게 할 수는 없다.
(적당한 p를 결정하는 문제는 나중에 다룬다)
Activation Function
-
Activation Function으로
Step Function을 사용했을 경우,Hard 의사결정(영역을 점으로 변환)이었다.
나머지 Activation Function으로Soft 의사결정(영역을 영역으로 변환)을 내릴 수 있다.
➡️ Soft 의사결정을 내릴 수 있게 하는 Activation Function에 대해 알아보자.(b ~ d)
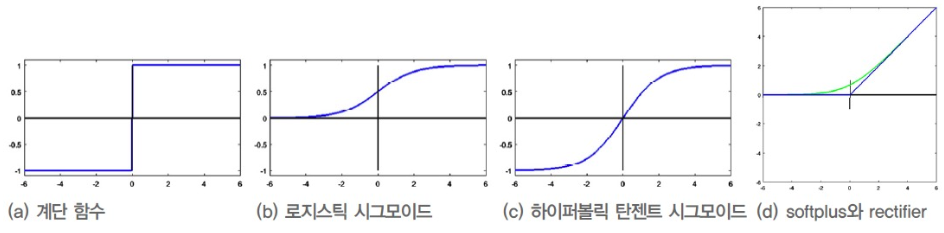

-
Sigmoid Function,Hyperbolic Tangent Function:- 둘 다 매개변수 에 따라 기울기가 결정된다.
가 무한대이면, Step Function이 된다. - 각각 (0 ~ 1), (-1 ~ 1) 사이의 실수를 출력하므로,
더 정확한 의사결정 또는 추가적인 추론 등에 활용할 수 있다. - 또한 학습 과정에서는 함숫값()와 1차 도함수값()를 많이 계산하는데,
Sigmoid의 1차 도함수는 로서
함숫값() 자체를 포함한다.
따라서 둘 다 1차 도함수 계산이 빠르다. - 학습 도중에 gradient가 점점 작아져 결국 0에 소멸하는
Gradient Vanishing 문제가 발생한다.
- 둘 다 매개변수 에 따라 기울기가 결정된다.
-
Retifier Linear Unit(ReLU) Function:- ReLU는 Sigmoid, Hyperbolic Tangent Function의 Gradient Vanishing 문제를
완화해줄 수 있다. - 또한, ReLU function의 Gradient는 비교 연산 한 번으로 계산할 수 있어서
딥러닝의 속도 향상에 매우 유용하다. - 하지만 음수를 모두 0으로 대치하기 때문에 문제가 발생하기 때문에 여러 문제가 발생한다.
(문제 해결을 위한 여러 변종이 개발되었는데, 이는 Chap 5.2.5에서...)
- ReLU는 Sigmoid, Hyperbolic Tangent Function의 Gradient Vanishing 문제를
Perceptron은 Step Function,
MLP는 Logistic Sigmoid와 Hyperbolic Tangent Function,
딥러닝은 ReLU를 주로 사용한다.
구조
-
위에서 XOR Classification을 구현했던 MLP를 좀 더 일반화하면 다음과 같다.
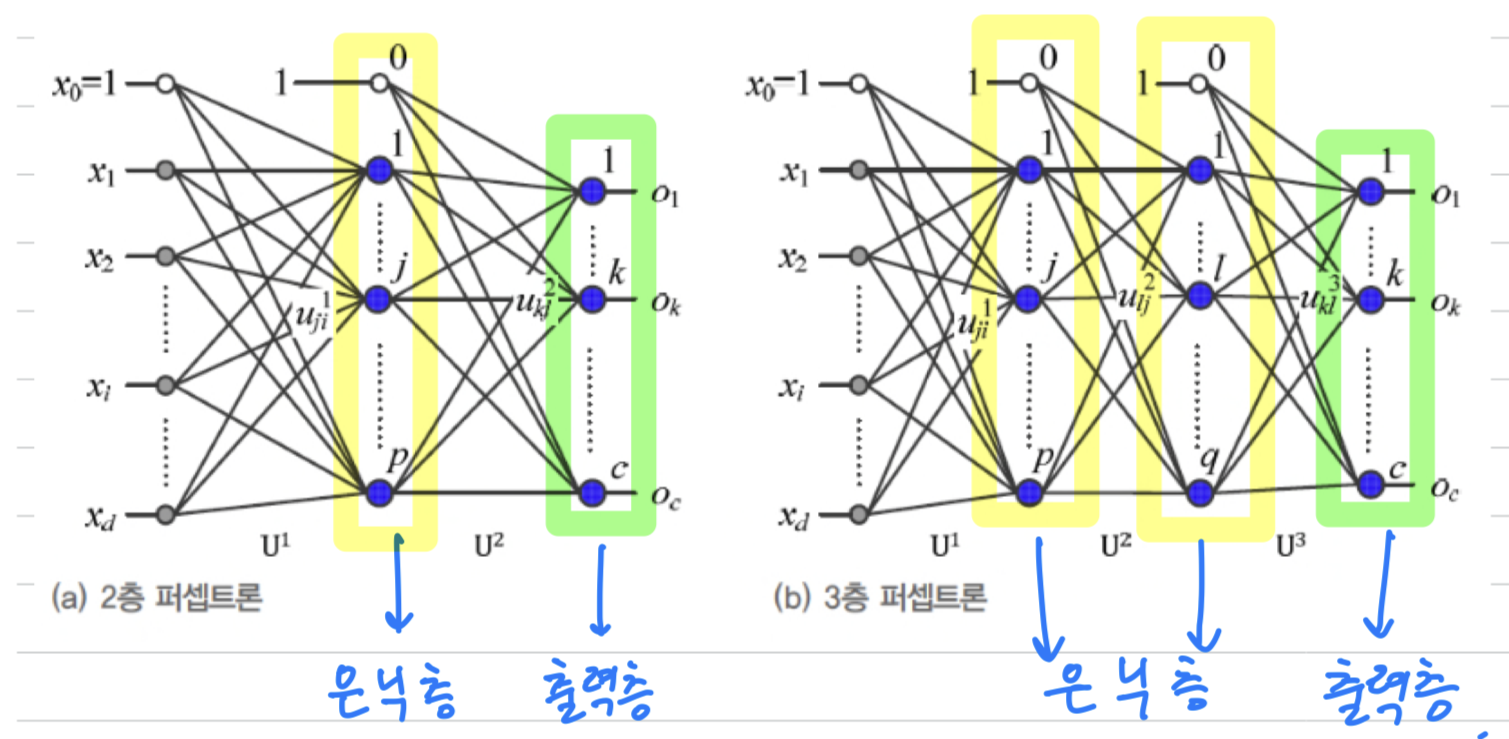
-
Multi-Layer Perceptron(MLP, 다층 퍼셉트론): Perceptron(단층 Perceptron)과 달리 층이 여러 개이기 때문에 MLP라고 한다. -
Hidden Layer(은닉층): 입력층과 출력층 사이에 놓인 층.
입력층은 주어진 Feature vector를 입력하는 곳이고,
출력층은 신경망의 최종 출력이 나오는 곳으로서 두 곳 모두 값을 관찰할 수 있는 반면,
은닉층은 계산의 중간과정으로서 보이지 않는 곳이라는 뜻에서 '은닉'이라는 명칭이 붙음. -
은닉층이 약 4개 이상이 되면
Deep Neural Network로 취급한다.
Deep Neural Network을 학습시키는 알고리즘을Deep Learning이라고 한다.
(딥러닝은 Chap 4에서 공부..)
-
가중치 표기법
(a) : 2층 Perceptron의 parameter는
입력층과 은닉층을 연결하는 가중치() 와
은닉층과 출력층을 연결하는 가중치()가 있다.
가중치 표기법은 다음과 같다.
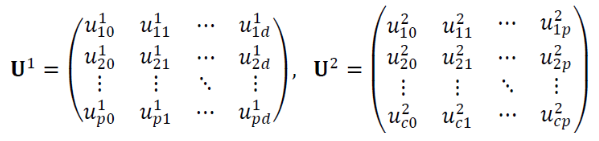

Hyperparameter
-
Train Set이 주어져 문제가 확정되면 MLP의 구조 중
input node와 output node의 개수는 자동으로 정해진다.
(ex. 숫자 인식 Train Set의 input node는 (d+1), output node는 10(c)개)하지만 은닉층에 있는 node 개수 는 사용자가 지정해야 한다.
이렇게 사용자가 지정해야 하는 parameter를
hyper parameter(hidden node 개수, Activation Function 종류, Running Rate 등)라고 한다.hidden node 개수 가
너무 크면 Overfitting,
너무 작으면 Underfitting의 위험이 있으므로 적절한 값을 선택해야 한다.
(hyper parameter를 최적화하는 문제는 Chapter 5에서...)
병렬분산 구조
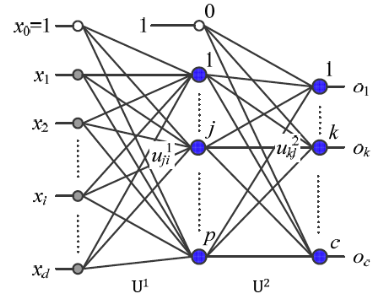
-
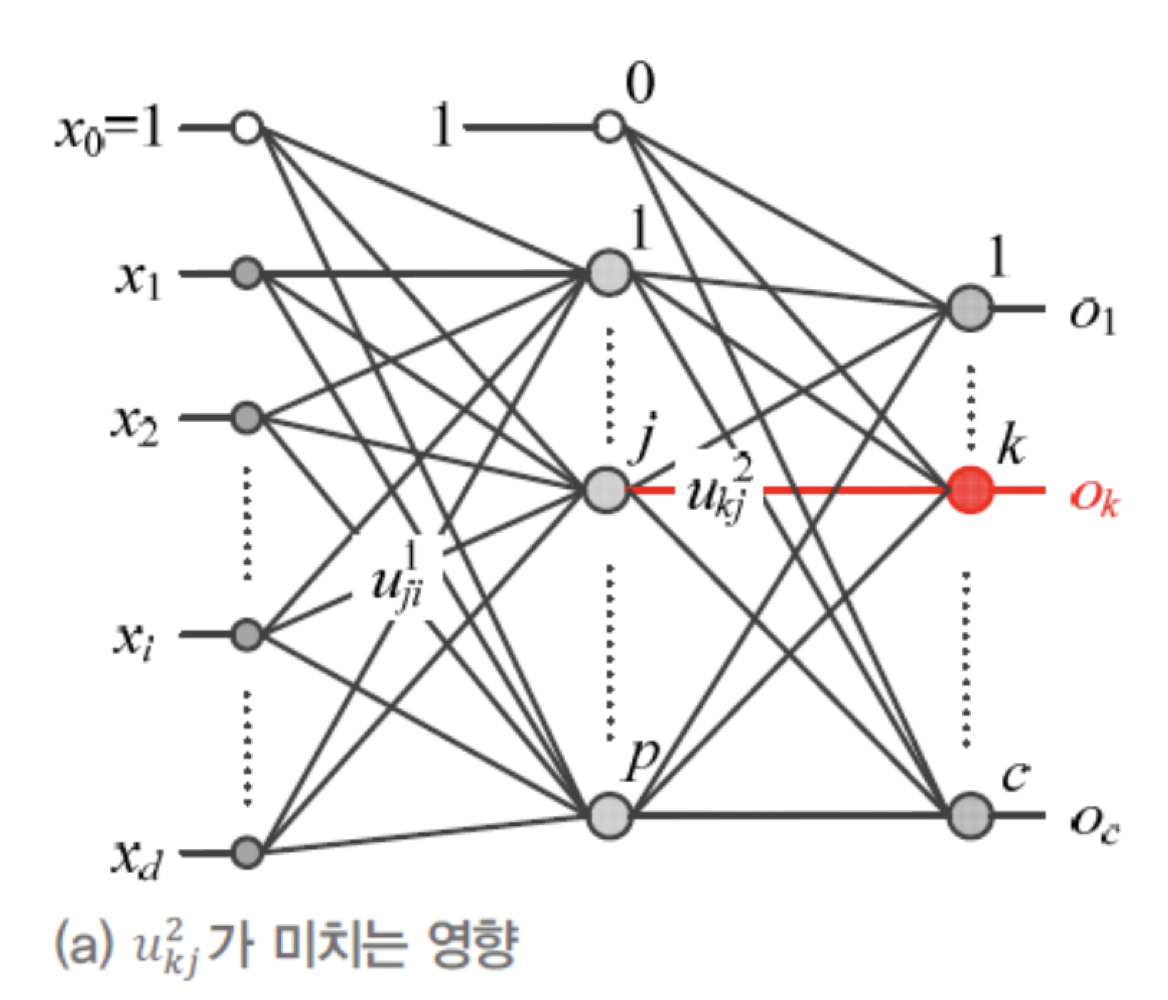
위의 그림에서 는 은닉층의 모든 node에 영향을 미친다.
그리고 그 결과는 또 출력층의 모든 node에 영향을 미친다.
모든 입력 node가 이러한 방식의 영향을 미치므로 신경망은분산처리를 한다고 한다. -
은닉층에 있는 한 node가 라는 시간을 소비한다면,
은닉층이 계산을 마치는 데 라는 시간이 걸린다.
그런데 각 노드는 각자 독립적으로 자신의 값을 계산할 수 있으므로
GPU와 같은 병렬처리기를 사용하면 라는 시간에 계산을 마칠 수 있다.
따라서, MLP는병렬처리를 한다고 한다.
(물론 번째 층의 계산 결과를 에서 번째 층의 입력으로 사용하기 때문에
인접한 층 사이에서는 계산이 순차적으로 일어난다.)
MLP는 분산처리와 병렬처리를 수행하므로 병렬분산 구조라고 할 수 있다.
동작
-
MLP의 동작을 간략하게 생각해보면,
다음과 같이 vector 를 vector 로 mapping하는 함수로 볼 수 있다.
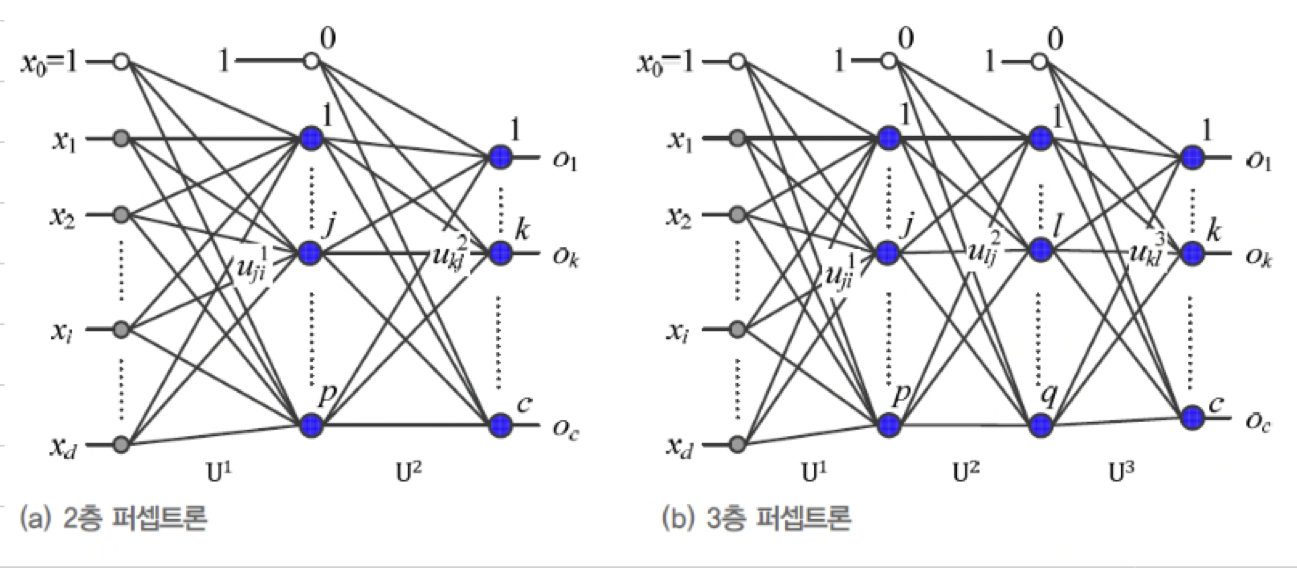
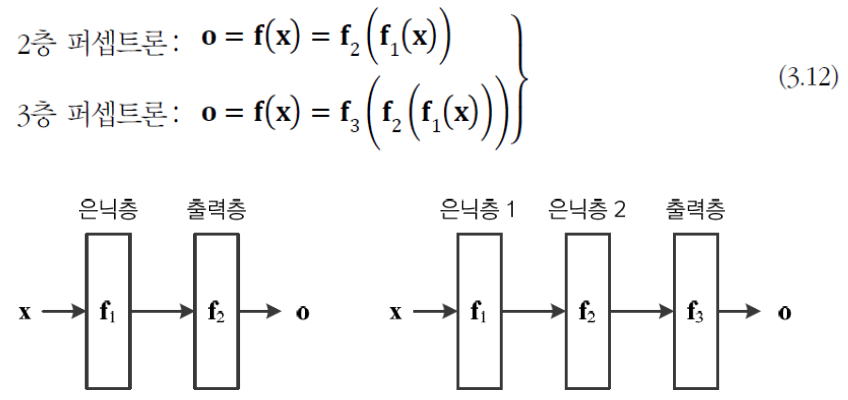
- Deep Neural Network는
와 같이 동작한다.
- Deep Neural Network는
-
MLP(2층 Perceptron)의 동작을 행렬로 표기하면 다음과 같다.
은닉층은 Feature Extractor이다.
- XOR 문제를 풀었던 다음의 MLP를 통해
원래 특징 공간은 Linear Non-Separable했었는데,
새로운 특징 공간에서는 Lienar Separable해졌다.
 현대 기계 학습의 주류인 딥러닝에서는,
현대 기계 학습의 주류인 딥러닝에서는,
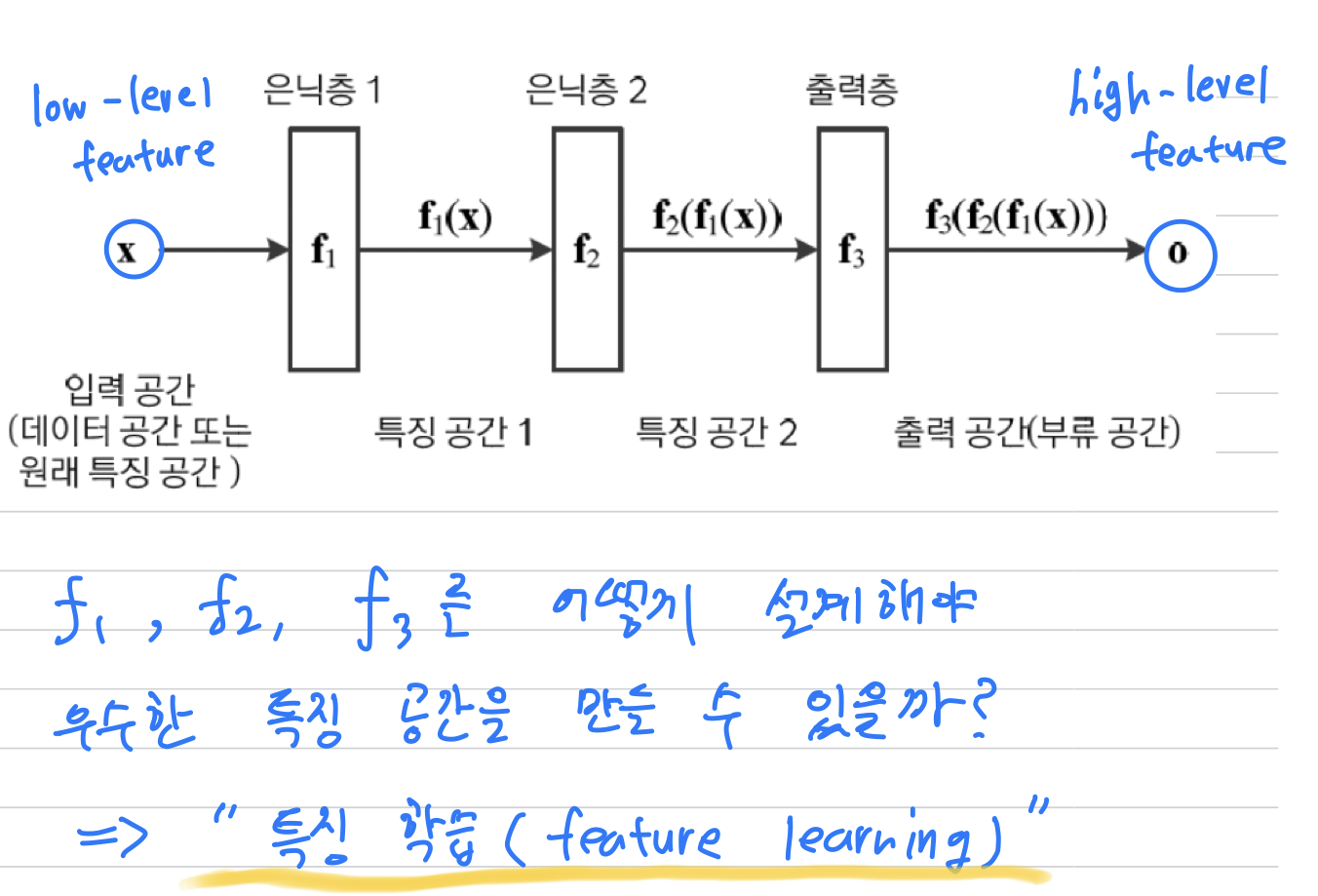
여러 단계의은닉층이 자동으로 계층적인 feature를 추출하는 접근방법을 사용한다.
계층적은 앞 쪽에 있는 low-level feature를 뒤 쪽에 있는 은닉층들이 입력받아
추상화된 high-level feature을 추출하는 방식이다.
- 따라서
은닉층()은Feature Extractor로서 역할을 한다.
또한 은닉층을 어떻게 설계해야 우수한 특징 공간을 만들 수 있을지 자동 설계하는 것이 중요해지고 있고, 그것을특징 학습(feature learning)이라고 한다.
오류 역전파 알고리즘
- MLP의 많은 pararmeter를 추정할 마땅한 학습 알고리즘으로
Error Backpropagation(오류역전파)가 등장한다.
이 알고리즘은 현재 기계 학습에서 대세인 딥러닝의 모태가 된다.
목적함수의 정의
-
Train Set이 n개의 Sample이 있고,
다음과 같은 특징 벡터 행렬 와 소속 부류 행렬 가 있다고 가정하자.- = {} [], ( : 특징 벡터의 차원)
- = {} [], ( : 부류의 개수)
➡️ 기계학습의 궁극적인 목적은
를 완벽하게 로 Mapping하는 최적의 함수 를 알아내는 것이다.
➡️ 다시 말해, 모든 Sample을 옳게 분류하는 분류기 를 찾는 것이다.
➡️ 하지만 현실적으로 완벽한 분류기는 불가능하므로, 근사 최적해를 구한다.
➡️ 따라서 기계학습이 해야 할 일을 다음과 같이 기술할 수 있다.
➡️ MLP의 출력 와 주어진 부류 정보 의 차이를 최소화 하는
최적의 paramter 를 찾아야 한다.
-
() 식을 토대로 목적함수를 설계하면 다음과 같다.
목적함수를 적용하여 의 부류 벡터 와 출력 의 MSE(Mean-Squared Error)를 계산한다.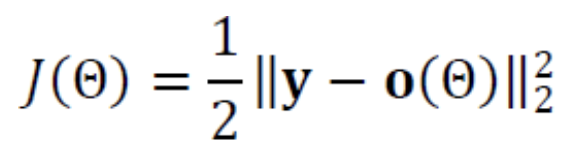
Online Mode(Stochastic Gradient Descent에 사용되는 방법):
Sample을 순차적으로 처리하면서 모델을 학습시키는 방식으로,
하나의 Sample에 대한 출력이 나올 때마다 parameter update.
➡️Batch Mode(Batch Gradient Descent에 사용되는 방법):
Sample을 한꺼번에 처리하면서 모델을 학습시키는 방식으로,
모든 Sample에 대한 출력이 나오면 parameter update.
➡️
오류 역전파 알고리즘 설계
-
수식 전개가 보다 간편한 온라인 모드(Stochastic Gradient Descent에 사용되는)로 선택
-
2 Layer Perceptron이라고 가정한다.
-
목적함수 는 다음과 같이 정의한다.
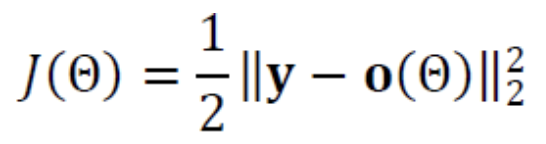
-
의 최저점을 찾아주는 Gradient Descent는 다음과 같다.
( : Running Rate)
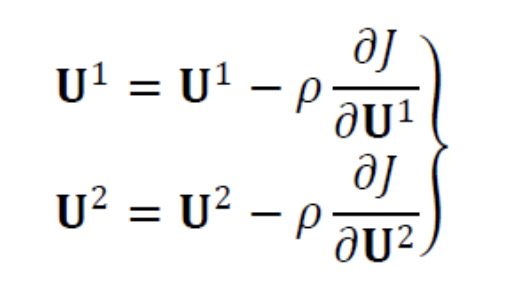
-
-
위의 수식을 바탕으로 MLP 알고리즘을 구체화 하면 다음과 같다.

오류 역전파의 유도
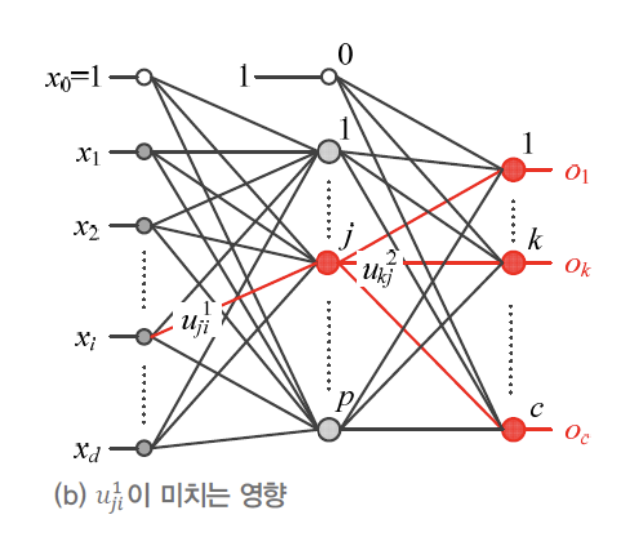
- 위의 MLP 알고리즘에서,
라인 6의 각각의 도함수값은 목적함수 를 과 로 미분하여 구할 수 있다.
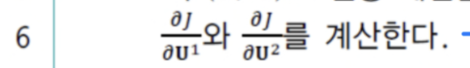
- 수식 전개를 간편하게 하기 위해서
를 구성하는 여러 weight 중 로 미분하는 과정을 보일 것이다.

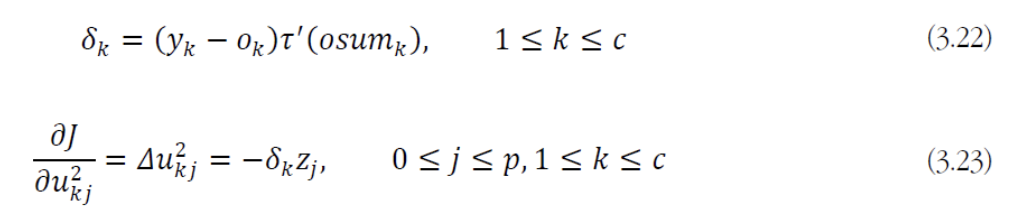
- 마찬가지로 수식 전개를 간편하게 하기 위해서
를 구성하는 여러 weight 중 로 미분하는 과정을 보일 것이다.
(는 보다 출력층에 미치는 영향이 더 넓어서 수식이 더 복잡해진다.)


- 위의 과정을 다시 살펴보자면,
feeforward(전방) 계산은 왼쪽에서 오른쪽으로(➡️) 계산했지만,
위의 과정(오류 역전파)은 오른쪽에서 왼쪽으로(⬅️) 계산한다.
왜냐하면 출력 vector 와 부류 vector 의 차이에 따라 Gradient값이 결정되는데,
출력층에 바로 연결된 가중치가 이기 때문에 를 먼저 처리한다.
그런 다음 의 계산 결과를 이용하여 를 처리한다.
이처럼 전방 계산과 달리 계산이 반대 방향으로 흐르고,
계산 과정에서 와 의 차이, 즉 오류를 줄이는 방향으로 전파하기 때문에
오류 역전파(Error Backpropagation)라는 이름이 붙었다.
오류 역전파를 이용한 학습 알고리즘
-
위에서 유도한 오류 역전파 공식을 구체화하면 다음과 같다.
-
Sample 하나의 gradient를 계산한 후 즉시 weight를 갱신한다.
이러한 방식을stochastic learning또는online learning이라고 한다.
(추후에는 여러 Sample의 gradient 평균을 구한 다음 한꺼번에 weight를 갱신하는
미니배치 방식을 공부할 것이다.. 현대 기계 학습은 미니배치 방식을 주로 사용한다.)

- 라인 3 ~ 라인 14는 한 epoch을 구성함.
- 라인 3에서 의 순서를 섞고, 한 번에 Sample 하나씩 순서대로 처리하기 때문에
모든 Sample에 한 번씩 기회가 주어진다. - 만약 선택된 Sample의 빈도도 random하게 하고 싶다면, 다음과 같이 수정하면 된다.

-
행렬 표기로 나타내면 다음과 같다.
(GPU를 사용하면 행렬 연산 속도는 매우 향상된다.)

- : Hadamard product(요소별 곱)
미니배치 스토캐스틱 경사 하강법
-
앞서
Stochastic Gradient Descent(SGD)에서는
한 번에 하나의 Sample의 gradient를 계산한 다음 weight를 갱신했다.
(한 번에 처리하는 Sample 수를 라고 하면, )
➡️ 이 과정을 모든 Sample에 수행하면 한 epoch가 지나는데,
최저점에 수렴할 때까지 여러 epoch을 반복한다.
➡️문제점: 실제 데이터에 실험하면,
Sample로 계산한 gradient는 잡음을 많이 포함하게 되어
최저점을 찾아가는 경로가 매개변수 공간에서 갈팡질팡하는 경향을 보인다.
(수렴하는 데 시간이 오래 걸린다.) -
또한
Batch Gradient Descent(BGD)방식은
모든 Sample의 gradient를 계산한 다음 평균 gradient를 구하여 한꺼번에 갱신했다.
(한 번에 처리하는 Sample 수를 라고 하면, )
➡️ 이 방식도 또한 극단적인 방식으로, 여러 문제점이 존재한다.
- 모든 Sample의 gradient를 계산한 다음 평균 grdient를 구하여 한꺼번에 갱신하면 된다.
이 방식을Mini Batch Stochastic Gradient Descent라고 한다.
현대 기계학습에서는 Mini Batch SGD를 널리 사용하므로
mini batch를 생략하여 그냥SGD라고 부르기도 한다.
따라서 SGD가 진짜 SGD인지 Mini Batch가 생략된 SGD인지 잘 구별해야 한다.
- 이 방식은 훈련집합 에서 개의 Sample을 무작위로 뽑아 mini batch를 구성하고,
mini- batch의 평균 gradient로 weight를 갱신한다.
(를 보통 수십~수백 정도의 크기로 설정한다.) - 장점 : GPU 병렬처리에 유리하여 수렴 속도 빨라짐.

- mini batch 방식에서는 mini batch를 random하게 뽑기 때문에
학습이 완료될 때까지 한 번도 학습에 참여하지 않는 Sample이 있을 수 있다.
하지만 mini batch가 모든 Sample의 대략적인 대표성을 띠므로,
이러한 현상이 mini batch 방식의 성능에 해를 끼치지 않는다고 입증되었다.
- mini batch 방식에서는 mini batch를 random하게 뽑기 때문에
다층 퍼셉트론에 의한 인식
-
학습을 마친 MLP는 응용 현장에 설치하여 활용되는 인식 단계로 넘어간다.
-
이 단계를
Test 단계또는예측 단계라고 한다. -
출력 벡터 에서 가장 큰 값을 가지는 부류를 찾는다.

- 라인 6에 들어갈 수식은 다음과 같다.
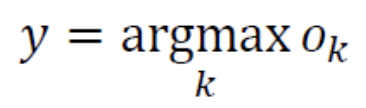
- 라인 6에 들어갈 수식은 다음과 같다.
-
Test 단계의 알고리즘은 전방 계산만 사용하므로 매우 빠르다.
-
신경망은 Traininig(학습)을 마치면, Train Set을 가지고 있을 필요가 없다.
대신 weight를 저장한다.- Train Set은 만큼의 메모리가 필요하지만.
weight는 만큼의 메모리만 필요하다.
➡️ 예를 들어, MNIST에서 , 이므로
특징 하나가 4Byte를 사용한다면,
Train Set은 의 메모리를 사용하지만,
weight의 node를 100개로 한다면 면 충분하여 메모리 효율이 매우 높다.
- Train Set은 만큼의 메모리가 필요하지만.
Test 단계(인식 단계)는 Train 단계보다 빠르고, 메모리 효율이 좋다.
다층 퍼셉트론의 특성
오류 역전파의 빠른 속도
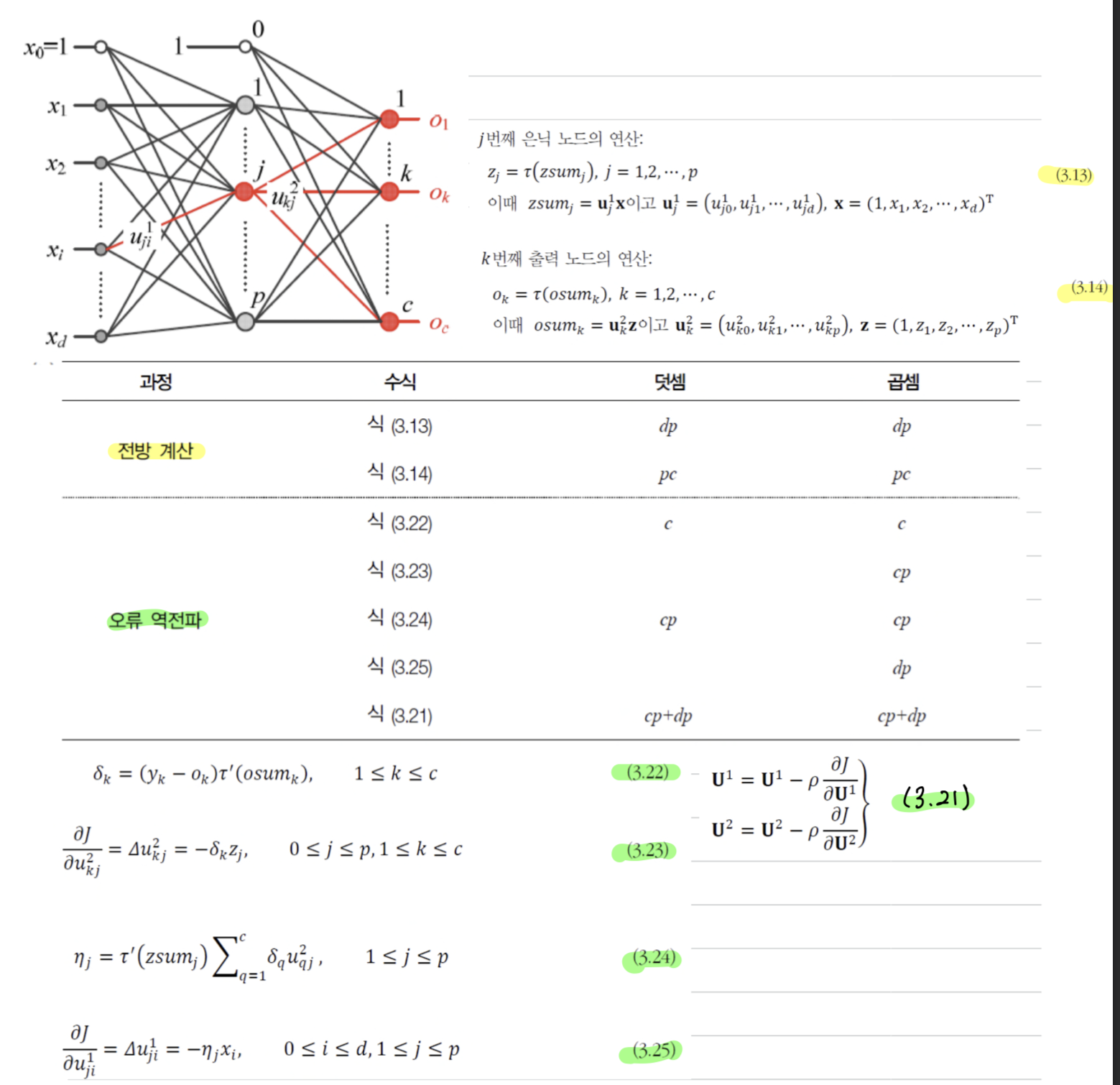
- 위의 그림은 Activation Function 연산을 제외한 덧셈과 곱셈의 횟수를 보여 준다.
- 전방 계산은
- 오류 역전파는 만큼 소요된다.
( = 입력 노드 개수, : 은닉 노드 개수, : 출력 노드 개수)
- 보통의 경우, 가 의 개수보다 훨씬 크기 때문에
전방 계산과 오류 역전파 계산의 격차는 더 줄어든다.
➡️ 오류 역전파 계산 생각보다 오래 걸리지 않는다는 것이다.
전방 계산보다 약 1.5 ~ 2배의 시간이 걸릴 것으로 예상할 수 있다. - 실제 Train 알고리즘은 수렴할 때까지 epoch을 반복하며, epoch마다 모든 Sample을 처리해야 한다.
따라서 Train 알고리즘의 계산 시간을 점근적 시간 복잡도로 쓰면
이다. ( : Sample 수, : epoch 수)
모든 함수를 정확하게 근사할 수 있는 능력
- Hornik(호닉)의 주장 : "...standard multilayer feedforward netowrk architectures using arbitary squashing functions can approximate virutally and function or interest to any desired degree of accuracy, provised sufficiently many hidden unit sare available, ...
MLP는 Universal Approximator(범용 근사자)이다."
➡️ (요약) "은닉층을 하나만 가져도 노드가 충분히 많다면, 활성함수로 무엇을 사용하든 표준 MLP는 어떤 함수라도 원하는 정확도만큼 근사화할 수 있다."
- 하지만 현실은 그렇지 않지만
은닉층이 하나뿐이어도 충분하다는 이론에 따라 은닉층이 하나인 신경망을 개선하려는 노력과
은닉층을 여럿으로 늘려 깊은 신경망으로 확장하여 개선하는 두 줄기의 접근 방법이 있고,
그러한 방법으로 문제를 풀 수 있다는 희망을 준다.
성능 향상을 위한 휴리스틱의 중요성
휴리스틱(heuristic): 주어진 문제를 해결하기 위한 규칙이나 방법- 대부분 데이터가 충분하지 않고, 잡음이 섞여있으며
미숙한 신경망 구조를 사용하는 등의 여러가지 문제 때문에
기초적인 알고리즘만으로는 만족할 만한 성능을 얻기 어렵다.
따라서 신경망 연구자들은 성능을 높일 수 있는 갖가지 휴리스틱을 개발하고 공유하는 연구 문화를 누려왔다.
휴리스틱 연구 결과를 잘 정리한 책인 "Nueral Networks : Tricks of the Trade"에서 나오는중요한 쟁점들.아키텍처: 은닉층과 은닉 노드의 개수를 정해야 한다.
은닉층과 은닉 노드를 늘리면 신경망의 용량은 커지는 대신,
추정할 매개변수가 많아지고 학습 과정에서 Overfitting할 가능성이 커진다.
따라서 현대 기계 학습은 복잡한 모델을 사용하되, 적절한 규제 기법을 적용하는 경향이 있다.초깃값: 보통 난수를 생성하여 설정하는데, 값의 범위와 분포가 중요하다.(Chap 5.2)학습률: 처음부터 끝까지 같은 학습률을 사용하는 방식과 처음에는 큰 값으로 시작하고
점점 줄이는 적응적 방식이 있다. (Chap 5.2)활성함수: 초창치 MLP는 주로 sigmoid나 tanh 함수를 사용했는데,
은닉층의 개수를 늘림에 따라 gradient 소멸 등의 문제가 발생한다.
따라서 DNN은 주로 ReLU 함수를 사용한다. (Chap 5.2)
- 위의 쟁점들은 DMLP(Deep Multiple Layer Perceptron)과 CNN에 적용된다.
- 쟁점마다 매개변수가 있는데,
이 매개변수들을 잘 설정해야 만족할 만한 성능을 얻을 수 있다.
이 매개변수를 Hyper parameter라고 한다. (Hyper Parameter 최적화 기법은 Chap 5.5)