다양한 그래프 알고리즘(2) : 최소 신장 트리

신장 트리

하나의 그래프가 있을 때 모든 노드를 포함하면서 사이클이 존재하지 않는 부분 그래프

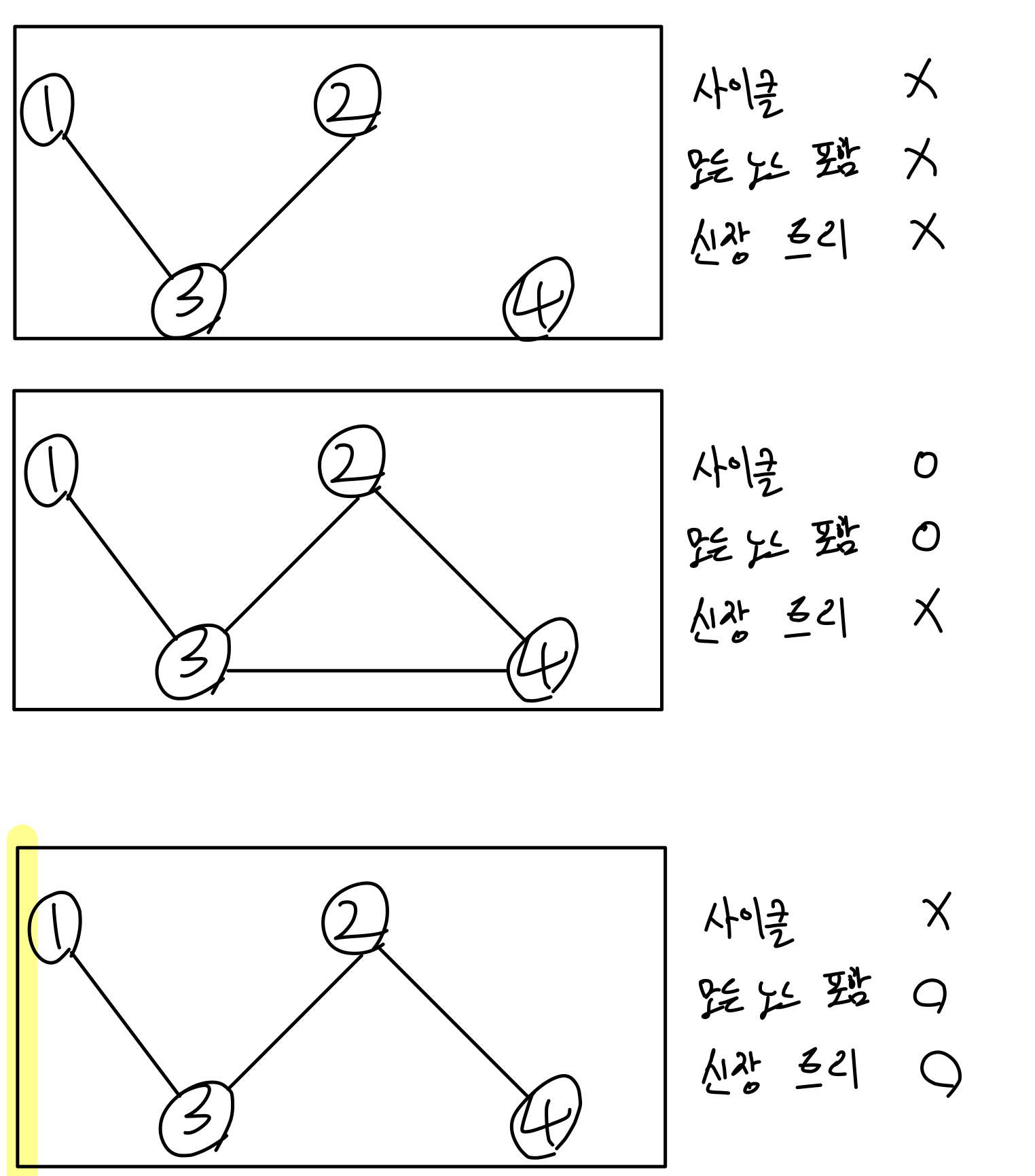
최소 신장 트리 (Minimum Spanning Tree, MST)

최소한의 비용으로 신장 트리를 찾아야 할 때가 있다.

예를 들어 2개의 도시A에서 도시B로 이동하는 경로가 반드시 존재하도록 도로를 설치하고자 하고, 모든 도시를 '연결'할 때, 최소한의 비용으로 연결하려는 경우가 있다.

대표적인 최소 신장 트리 알고리즘으로는 크루스칼 알고리즘(Kruskal Algorithm)이 있다.

• 최소 신장 트리는 노드가 N개일 때, 항상 간선의 개수가 N-1개이다.

아이디어 :

1. 간선 데이터를 비용에 따라 오름차순으로 정렬한다.
2. 간선을 하나씩 확인하며 현재의 간선이 사이클을 발생시키는지 확인한다.
   1) 사이클이 발생하지 않는 경우 최소 신장 트리에 포함시킨다.
   2) 사이클이 발생하는 경우 최소 신장 트리에 포함시키지 않는다.
3. 모든 간선에 대하여 2. 과정을 반복한다.
   (n개의 노드가 있을 때, n-1개의 간선을 찾았으면 break)

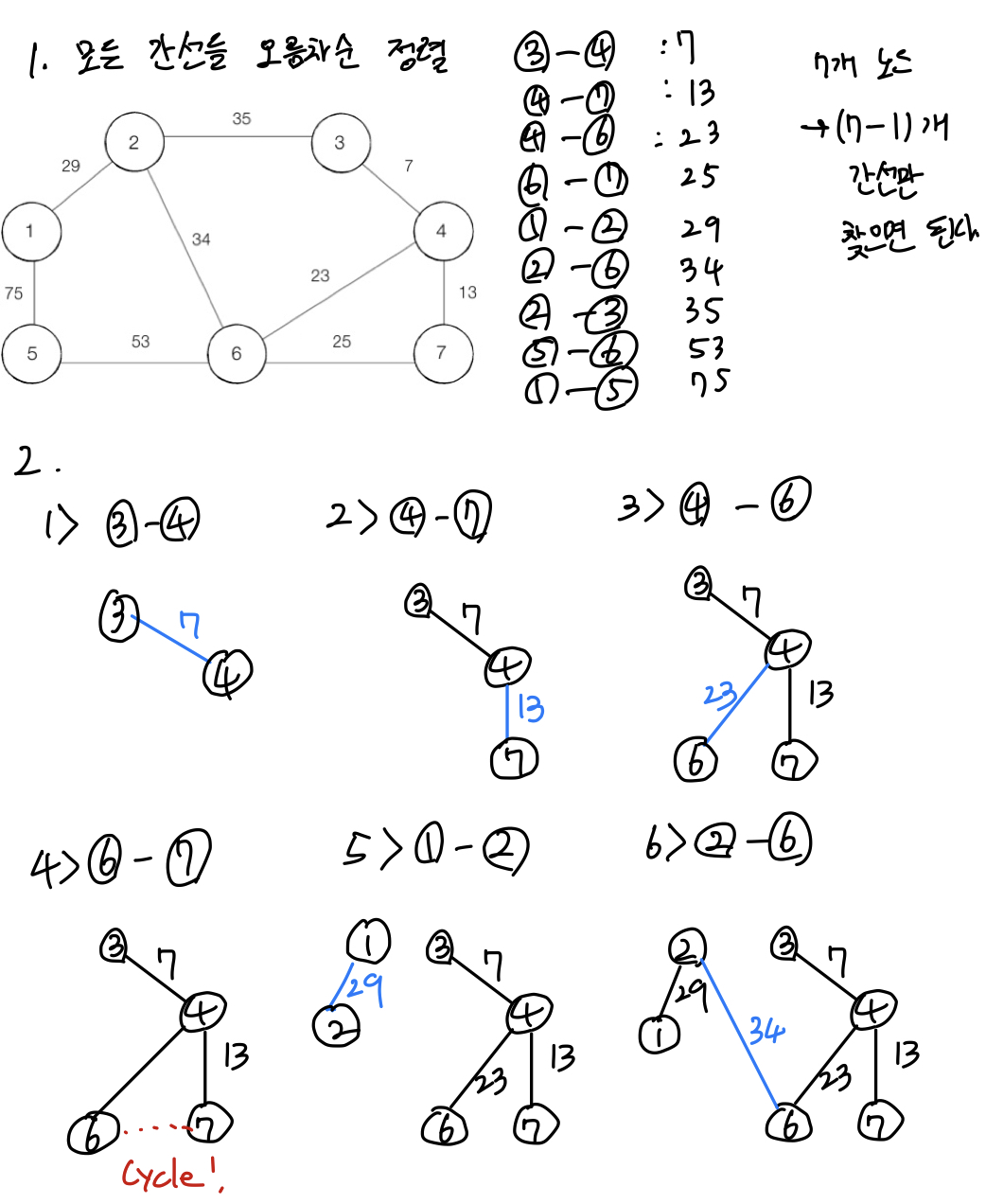
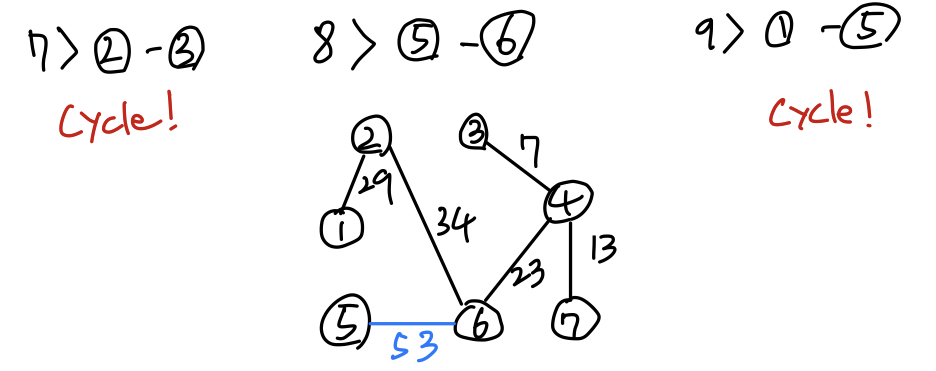
노드의 개수가 7개이고, 찾아야할 간선의 개수는 7-1 = 6이므로
9> 를 수행하지 않았어도 됐다. (8>에서 6개의 간선을 모두 찾았기 때문)

시간 복잡도 :

크루스칼 알고리즘은 간선의 개수가 E개일 때, $O(Elog(E))$의 시간 복잡도를 가진다.
왜냐하면 크루스칼 알고리즘에서 가장 오래 걸리는 부분이 모든 간선을 오름차순 정렬하는 작업이기 때문이다.
서로소 집합 알고리즘은 정렬 알고리즘보다 작으므로 무시한다.

cpp로 구현한 크루스칼 알고리즘 :

#include <iostream>
#include <vector>

using namespace std;

int find_parent(int* _parent, int _data) {
    if(_parent[_data] != _data) {
        _parent[_data] = find_parent(_parent, _parent[_data]);
    }
    return _parent[_data];
}

void union_parent(int* _parent, int _v1, int _v2) {
    int v1_parent = find_parent(_parent, _v1);
    int v2_parent = find_parent(_parent, _v2);
    if(v1_parent < v2_parent) {
        _parent[_v2] = _v1;
    }
    else {
        _parent[_v1] = _v2;
    }
}

int main(void){


    int v, e;
    int* parent = new int[v+1];

    vector<pair<int, pair<int, int>>> edges; // cost, {v1, v2}
    int res = 0;

    cin >> v >> e;

    for (int i = 0; i < v+1; i++)
    {
        parent[i] = i;
    }
    for (int i = 0; i < e; i++)
    {
        int v1, v2, cost;
        cin >> v1 >> v2 >> cost;
        edges.push_back({cost, {v1, v2}});
    }
    // 간선 오름차순 정렬
    sort(edges.begin(), edges.end());
    
    for (int i = 0; i < edges.size(); i++)
    {
        int cost = edges[i].first;
        int v1 = edges[i].second.first;
        int v2 = edges[i].second.second;
        if(find_parent(parent, v1) == find_parent(parent, v2)){
            continue;
        }
        else {
            union_parent(parent, v1, v2);
            cout << v1 << " --- " << v2 << endl;
            res += cost;
        }
    }

    cout << "total cost : " << res << endl;

    return 0;
}