바닥 공사
문제 설명 :
가로의 길이가 N, 세로의 길이가 2인 직사각형 형태의 얇은 바닥이 있다.
태일이는 이 얇은 바닥을 1 X 2의 덮개, 2 X 1의 덮개, 2 X 2의 덮개를 이용해 채우고자 한다.
이 때 바닥을 채우는 모든 경우의 수를 구하는 프로그램을 작성하시오.
예를 들어, 2X3 크기의 바닥을 채우는 경우의 수는 5가지이다.
첫째 줄에 N이 주어진다. (1 ≤ N ≤ 1,000)
첫째 줄에 2 X N 크기의 바닥을 채우는 방법의 수를 796,796으로 나눈 나머지를 출력한다.
아이디어 :
-
왼쪽부터 i-1까지 길이가 덮개로 이미 채워져 있으면 2x1 덮개를 채우는 하나의 경우 밖에 존재하지 않는다.
-
왼쪽부터 i-2까지 길이가 덮개로 이미 채워져 있으면 1x2 덮개 2개를 넣는 경우, 혹은 2x2의 덮개를 하나를 넣는 경우로 2가지 경우가 존재한다.
(2x1 덮개 2개를 넣는 경우가 배제된 이유는 1. 에서 중복이 있기 때문)
따라서 점화식을 세우면,
문제 풀이 :
#include <iostream>
using namespace std;
int main(void){
int n;
cin >> n;
int* dp_table = new int[n+1]{0};
dp_table[1] = 1;
dp_table[2] = 3;
for (int i = 3; i <= n; i++)
{
dp_table[i] = (dp_table[i-1] + 2*dp_table[i-2]) % 796796;
}
cout << dp_table[n] << endl;
return 0;
}효율적인 화폐 구성
문제 설명 :
N가지 종류의 화폐가 있다.
이 화폐들의 개수를 최소한으로 이용해서 그 가치의 합이 M원이 되도록 하려고 한다.
이때 각 화폐는 몇 개라도 사용할 수 있으며, 사용한 화폐의 구성은 같지만 순서만 다른 것은 같은 경우로 구분한다.
예를 들어 2원, 3원 단위의 화폐가 있을 때는 15원을 만들기 위해 3원을 5개 사용하는 것이 가장 최소한의 화폐 개수이다.
입력 조건 :
첫째 줄에 N,M이 주어진다(1<= N <= 100, 1<= M <= 10,000)
이후의 N개의 줄에는 각 화폐의 가치가 주어진다. 화폐의 가치는 10,000보다 작거나 같은 자연수이다.
출력 조건 :
첫째 줄에 경우의 수 X를 출력한다.
불가능할 때는 -1을 출력한다.
아이디어 :

- 입력받은 화폐 개수 m개만큼 반복문 실행하면서
- 중첩 반복분으로 목표 화폐 가치인 n까지 실행하여 DP Table을 update시킨다.
코드로 구현하면,
문제 풀이 :
#include <iostream>
#include <vector>
// 화폐 가치 m은 최대 10,000까지 입력이 되니까
// 갖고 있는 화폐로 화폐 가치를 만들 수 없는 경우, dp_table에 해당 값을 INF로 처리
#define INF 10001
using namespace std;
void showDP(vector<int>& _dp){
cout << endl;
for (auto i : _dp)
{
cout << i << " ";
}
cout << endl;
}
int main(void){
// 화폐 종류의 개수 n, 만들어야 할 화페 가치 m 입력받기
int n, m;
cin >> n >> m;
// 화폐 종류 입력받기
vector <int> currencies;
for (int i = 0; i < n; i++)
{
int temp;
cin >> temp;
currencies.push_back(temp);
}
// 모두 10,001원으로 초기화
vector<int> dp_table(m+1, INF);
dp_table[0] = INF;
// dp_table의 해당 화폐가치 인덱스에 1로 세팅
// 2원 -> dp_table[2] = 1
for (int i = 0; i < n; i++)
{
dp_table[currencies[i]] = 1;
}
// dp_table 업데이트 (Bottom-Up)
for (int i = 0; i < n; i++)
{
showDP(dp_table);
// j = currencies[i]인 이유 : 그 다음 화폐를 사용했을 때의 최소개수를 update시켜야 하니까
for(int j = currencies[i] ; j <= m ; j++){
// (i-k)원을 만들 수 있는 경우에만 DP Table update
if(dp_table[j - currencies[i]] != INF) {
dp_table[j] = min(dp_table[j], dp_table[j - currencies[i]] + 1);
}
}
}
if(dp_table[m] == INF){
cout << -1 << endl;
}
else{
cout << dp_table[m] << endl;
}
return 0;
}금광 문제
문제 설명 :
n x m 크기의 금광이 있습니다. 금광은 1 x 1 크기의 칸으로 나누어져 있으며, 각 칸은 특정한 크기의 금이 들어 있습니다. 채굴자는 첫 번째 열부터 출발하여 금을 캐기 시작합니다. 맨 처음에는 첫 번째 어느 행에서든 출발할 수 있습니다. 이후에 m번에 걸쳐서 매번 오른쪽 위, 오른쪽, 오른쪽 아래 3가지 중 하나의 위치로 이동해야 합니다. 결과적으로 채굴자가 얻을 수 있는 금의 최대 크기를 촐력하는 프로그램을 작성하세요.
입력 예시
2
3 4
1 3 3 2 2 1 4 1 0 6 4 7
4 4
1 3 1 5 2 2 4 1 5 0 2 3 0 6 1 2
출력 예시
19
16
아이디어 :
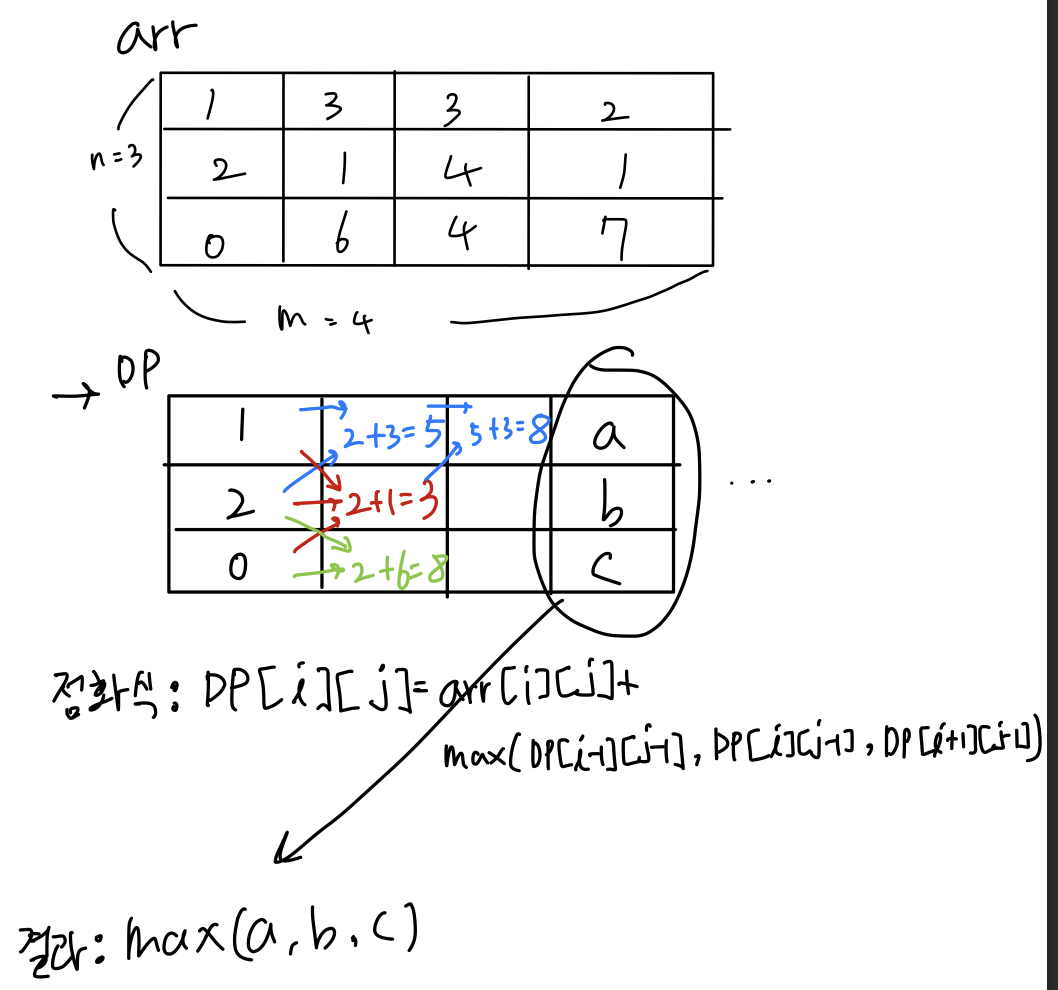
금광의 모든 위치에 대하여 다음의 세 가지만 고려하여 DP Table을 update시킨다.
- 왼쪽 위에서 오는 경우
- 왼쪽에서 오는 경우
- 왼쪽 아래에서 오는 경우
위의 3가지 경우 중 최대값 + 현재 금광의 값을
DP Table에 갱신시키면 되고,
가장 마지막 열 중에서 최대값이 결과가 된다.
문제 풀이 :
#include <iostream>
#include <vector>
using namespace std;
int main(void){
// test case 개수 입력 받기
int t;
cin >> t;
// test case만큼 실행
for (int _t = 0; _t < t; _t++)
{
// 행개수 n, 열개수 m 입력받기
int n, m;
cin >> n >> m;
// 행 개수 n, 열 개수 m, 0으로 초기화
vector<vector<int>> dp_table;
// dp_table 입력받기
for (int _n = 0; _n < n; _n++)
{
vector<int> temp_vec;
for (int _m = 0; _m < m; _m++)
{
int temp;
cin >> temp;
temp_vec.push_back(temp);
}
dp_table.push_back(temp_vec);
}
// dp_table 초기화 (첫 번째 열만 입력)
for (int _n = 0; _n < n; _n++)
{
dp_table[_n][0] = dp_table[_n][0];
}
// dp_table update (열 개수만큼 진행, 첫번째 열은 건너뜀)
for (int j = 1; j < m; j++)
{
for (int i = 0; i < n; i++)
{
int left_up=0, left=0, left_down=0;
// 왼쪽 위에서 오는 금광인 경우
if(i == 0) {
left_up = 0;
}
else {
left_up = dp_table[i-1][j-1];
}
// 왼쪽에서 오는 금광인 경우
left = dp_table[i][j-1];
// 왼쪽 아래에서 오는 금광인 경우
if(i == n-1) {
left_down = 0;
}
else {
left_down = dp_table[i+1][j-1];
}
dp_table[i][j] = dp_table[i][j] + max({left_up, left, left_down});
}
}
// 마지막 열에서 최대값이 결과이므로 출력
int max = 0;
for (int _n = 0; _n < n; _n++)
{
if(max < dp_table[_n][m-1]){
max = dp_table[_n][m-1];
}
}
cout << max << endl;
}
return 0;
}1로 만들기
문제 설명 :

아이디어 :
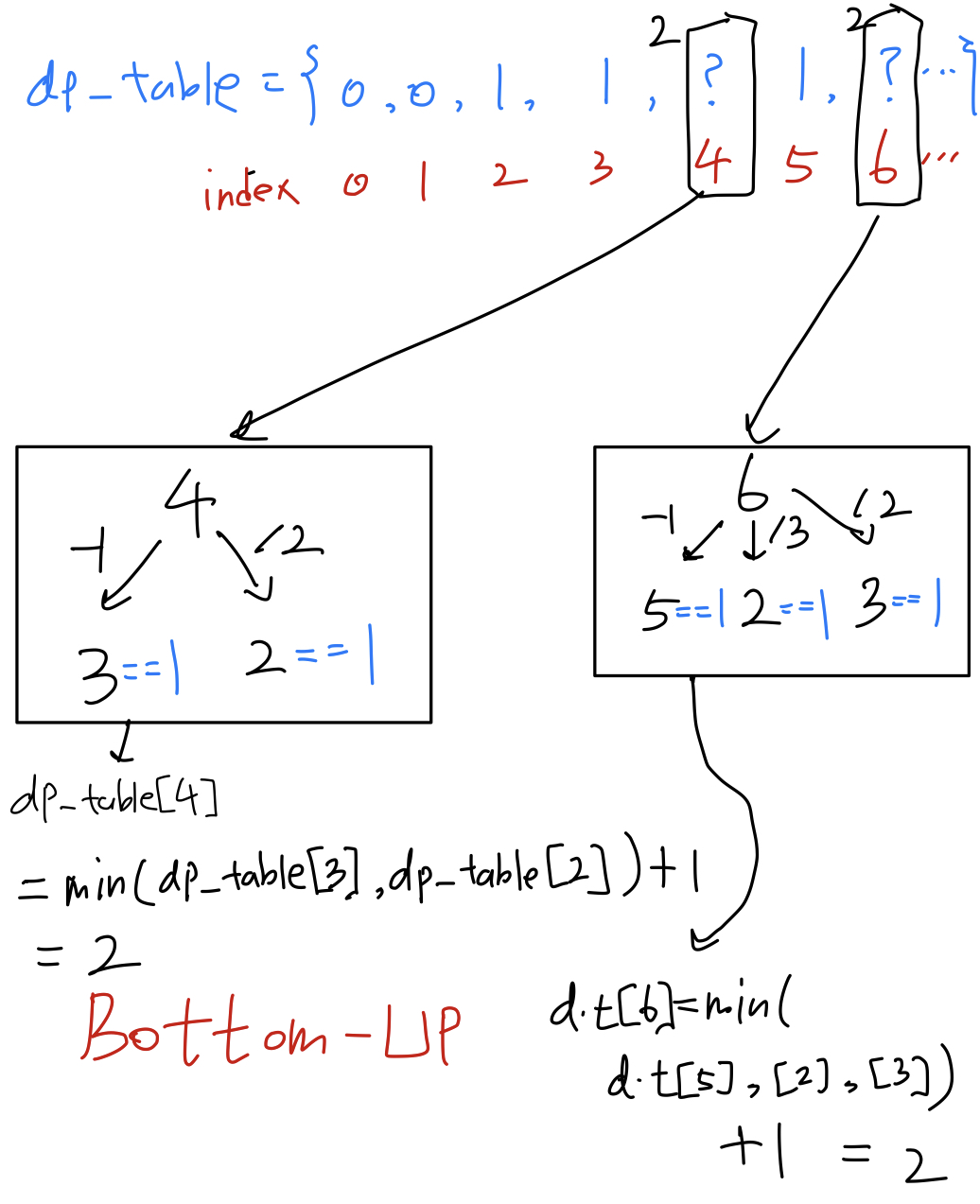
dp_table[0] ~ db_table[1] = 0
db_table[2] = 1 (2를 2로 나누었을 때, 1이 되므로)
dp_table[3] = 1 (3를 3로 나누었을 때, 1이 되므로)
dp_table[4] = ?
dp_table[5] = 1 (5를 5로 나누었을 때, 1이 되므로)
초기 dp_table[2], dp_table[3], dp_table[5]의 값을 이용하여
Bottom-Up 방식으로 dp_table[x]의 값을 구할 수 있다.
이것을 코드로 구현하면,
문제 풀이 :
#include <iostream>
using namespace std;
int main(void){
int x;
cin >> x;
// dp table 생성 후 0으로 초기화
int* dp_table = new int[x+1]{0};
// dp table 2, 3, 5 index 초기화
dp_table[2] = 1;
dp_table[3] = 1;
dp_table[5] = 1;
for(int i = 4 ; i <= x ; i++){
// 1을 뺐을 때의 연산횟수 == temp 라고 하자.
dp_table[i] = dp_table[i-1] + 1;
// temp와 2로 나눴을 때의 연산횟수 중, 더 작은 값으로 갱신
if(i % 2 == 0){
dp_table[i] = min(dp_table[i], dp_table[i/2]+1);
}
// temp와 3로 나눴을 때의 연산횟수 중, 더 작은 값으로 갱신
if(i % 3 == 0){
dp_table[i] = min(dp_table[i], dp_table[i/3]+1);
}
// temp와 5로 나눴을 때의 연산횟수 중, 더 작은 값으로 갱신
if(i % 5 == 0){
dp_table[i] = min(dp_table[i], dp_table[i/5]+1);
}
}
cout << dp_table[x] << endl;
return 0;
}개미 전사
문제 설명 :

아이디어 :
| 창고(N) | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| 식량(K) | 1 | 3 | 1 | 5 |
창고[0]까지만 존재한다고 가정했을 때, 얻을 수 있는 최대 식량 : dp_table[0] = 1
창고[1]까지만 존재한다고 가정했을 때, 얻을 수 있는 최대 식량 : dp_table[1] = 3
창고[2]까지만 존재한다고 가정했을 때, 얻을 수 있는 최대 식량
: max(창고[0] + 창고[2], 창고[1]) = dp_table[2] = 3
창고[3]까지만 존재한다고 가정했을 때, 얻을 수 있는 최대 식량
: max(창고[0]+창고[2], 창고[1]+창고[3]) = 8
-> dp_table = {1, 3, 3, 8, ...}
단, 창고[N]까지의 최대 식량을 구할 때 창고[N-1]를 털 것인지(a), 창고[N-2]를 털 것인지(b)를 결정해야 한다. (a)의 경우, 창고[N]은 털지 못하고 (b)의 경우, 창고[N]을 털 수 있기 때문에 max(a, b)를 선택하여 dp_table[N]을 갱신하면 된다.문제 풀이 :
#include <iostream>
using namespace std;
int main(void){
int n;
cin >> n;
int* warehouse = new int[n];
int* dp_table = new int[n] {0};
for (int i = 0; i < n; i++)
{
int k;
cin >> k;
warehouse[i] = k;
}
dp_table[0] = warehouse[0];
dp_table[1] = max(warehouse[0], warehouse[1]);
for (int i = 2; i < n; i++)
{
dp_table[i] = max(dp_table[i-1], dp_table[i-2] + warehouse[i]);
}
cout << dp_table[n-1] << endl;
return 0;
}병사 배치하기
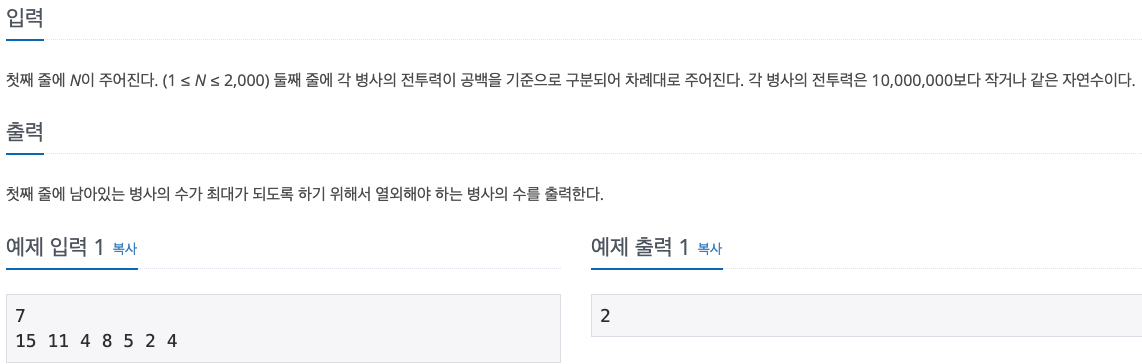
문제 설명 :
N명의 병사가 무작위로 나열되어 있다.
각 병사는 특정한 값의 전투력을 보유하고 있으며, 병사를 배치할 때는 전투력이 높은 병사가 앞쪽에 오도록 내림차순으로 배치를 하고자 한다.
배치 과정에서는 특정한 위치에 있는 병사를 열외시키는 방법을 이용한다.
그러면서도 남아있는 병사의 수가 최대가 되도록 하고 싶다. 병사에 대한 정보가 주어졌을 때, 남아있는 병사의 수가 최대가 되도록 하기 위해서 열외해야 하는 병사의 수를 출력하는 프로그램을 작성하시오.
아이디어 :
이 문제의 기본 아이디어는 "가장 긴 증가하는 부분 수열(Longest Increasing Subsequence, LIS)"이다.
LIS란 (Longest Increasing Subsequence)
➡️ LIS 문제는 주어진 수열에서
(조건1) 주어진 수열의 순서를 유지한 상태로
(조건2) 오름차순 부분 수열을 추출
(조건3) 추출한 부분 수열의 길이 Maximize
위 3가지 조건을 모두 만족하는 부분 수열을 LIS라고 한다.
예를 들어,
주어진 수열이 arr{4 2 5 8 4 11 15}라고 하자.
arr 수열에는 많은 부분 수열이 존재한다. {4}, {2 5}, {8 4 15} ...
하지만 (조건1), (조건2), (조건3)에 부합하는 부분 수열(LIS)은
{4 5 8 11 15}, {2 5 8 11 15} 두 개 밖에 없다.
그림으로 살펴보자.

LDS란 (Longest Decreasing Subsequence)
➡️ LDS 문제는 주어진 수열에서
(조건1) 주어진 수열의 순서를 유지한 상태로
(조건2) 내림차순 부분 수열을 추출
(조건3) 추출한 부분 수열의 길이 Maximize
위 3가지 조건을 모두 만족하는 부분 수열을 LDS라고 한다.
(LIS와 조건2에서 내리차순으로 부분 수열을 추출한다는 차이점만 존재)
그림으로 살펴보자.

본 문제는 가장 긴 감소하는 부분 수열을 찾는 문제(LDS)로 치환할 수 있다.
문제 풀이 :
n = int(input())
arr = list(map(int, input().split()))
dp_table = [1] * n
# LDS 알고리즘 수행
for i in range(1, n) :
for j in range(0, i) :
# 내림차순이 성립하면, DP Table update
if arr[j] > arr[i] :
dp_table[i] = max(dp_table[i], dp_table[j] + 1)
# 열외해야 하는 병사의 최소 수
print(n - max(dp_table))