https://www.acmicpc.net/problem/10830

문제

크기가 N*N인 행렬 A가 주어진다. 이때, A의 B제곱을 구하는 프로그램을 작성하시오. 수가 매우 커질 수 있으니, A^B의 각 원소를 1,000으로 나눈 나머지를 출력한다.

입력

첫째 줄에 행렬의 크기 N과 B가 주어진다. (2 ≤ N ≤ 5, 1 ≤ B ≤ 100,000,000,000)

둘째 줄부터 N개의 줄에 행렬의 각 원소가 주어진다. 행렬의 각 원소는 1,000보다 작거나 같은 자연수 또는 0이다.

출력

첫째 줄부터 N개의 줄에 걸쳐 행렬 A를 B제곱한 결과를 출력한다.

예제

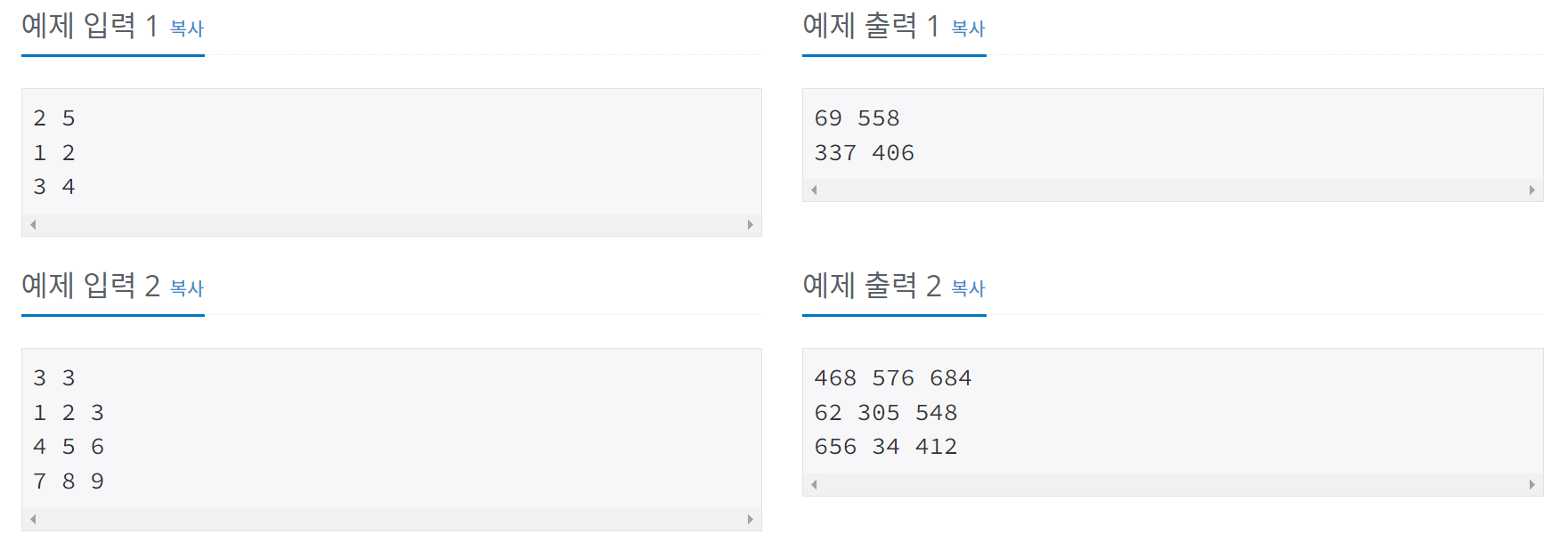
조건

• 시간 제한: 1초
• 메모리 제한: 256MB

---

🤔 행렬의 곱?

우선 난 전에도 행렬에 대해서 제대로 배운 적이 없기에... 행렬의 곱이 어떤 식으로 이루어지는 지도 알지 못했다. 그래서 여러 자료를 찾아본 결과, 겨우겨우 이해를 해낼 수 있었다!

행렬 A,B가 있다고 가정했을 때, 두 행렬의 곱을 AB라고 해보자

• 여기서 AB12 (=1행2열)를 구하는 방법은, 앞에 있는 A행렬의 1행과, 뒤에 있는 B행렬의 2열의 각 원소들을 곱한 후에 모두 더해주는 것이다.

이렇게만 보면 쉽게 이해가 되지 않는다. 아래 그림을 통해서 설명해보겠다.

예시

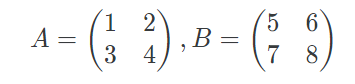
위와 같은 행렬 A와 B가 있다.

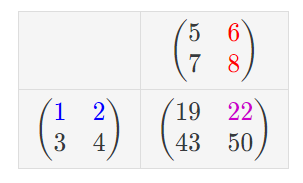
(출처 - 나무위키)

여기서 AB12는,

• (A행렬의 1행 첫번째 원소 1) X (B행렬의 2열 첫번째 원소6) = 6
• (A행렬의 1행 두번째 원소 2) X (B행렬의 2열 두번째 원소8) = 16

의 합으로 22라는 수가 결정되는 것이다.

코드

import sys
input = sys.stdin.readline
# 입력
N,B = map(int,input().split())
matrix = [list(map(int,input().split())) for _ in range(N)]

# 행렬 곱 함수
def multi_matrix(mat1,mat2):
    res = [[0]*N for _ in range(N)]
    for r in range(N):          # mat1에서의 행
        for c in range(N):      # mat2에서의 열
            for i in range(N):  # 각 행 or 열에서의 원소 위치
                res[r][c] += mat1[r][i] * mat2[i][c] % 1000
                
    return res
# 고속 거듭제곱 함수
def power(mat,n):
    if n == 1:     # n이 1이 될 때까지 재귀
        return mat # 입력받은 초기의 행렬
    else:
        temp = power(mat,n//2) # mat^(n//2)
        if n % 2 == 0: # 지수가 짝수인경우
            return multi_matrix(temp,temp)
        else:          # 지수가 홀수인경우
            return multi_matrix(multi_matrix(temp,temp),mat)

# 출력            
answer = power(matrix,B)

for r in answer:
    for c in r:
        print(c % 1000, end = ' ')
    print()

이제 행렬의 곱에 대한 이해를 마쳤으니, 이를 활용한 multi_matrix 함수를 만들 수 있다.

다음으로는 고속 거듭제곱 함수인 power인데, 기존과 다른 점은 숫자가 아닌 행렬이 인자로 들어간다는 것이다.

• 헷갈릴 수 있지만, 기존에는 일반 곱셈이기 때문에 temp * temp로 진행해주었던 것을, 행렬 곱셈이기에 multi_matrix(temp,temp)로 바꿔주었다고 생각하면 된다.

n == 5일 경우를 예로 들어보겠다.

• n == 1때까지 재귀를 진행하면, 초기 상태의 행렬(=행렬의 1승)을 리턴한다.

• 이를 리턴받은 n은 2이므로, 행렬^1 * 행렬^1인 행렬^2를 리턴한다.

• 다음으로 이를 리턴받은 n은 5이므로, 행렬^2 * 행렬^2 * 행렬^1인 행렬^5를 최종적으로 리턴한다.

• 이렇게 되면 answer에는 행렬의 5승이 정상적으로 들어가게 된다.

출력을 할 때에도, 값이 커짐을 방지하여 1000의 나머지만을 출력한다.

---

느낀 점 & 배운 점

1. 처음에는 대체 이게 무슨 문제지.. 한참을 고민하고 찾아보았던 것 같다. 그래도 끙끙대며 시간을 쓰니 결국 이해를 할 수 있어서 뿌듯했다!

2. 행렬의 곱과 고속 거듭제곱 함수를 모두 생각해 볼 수 있는 좋은 문제였다고 생각한다.