[Python] S2_18222_투에-모스 문자열 🔟

https://www.acmicpc.net/problem/18222

문제

0과 1로 이루어진 길이가 무한한 문자열 X가 있다. 이 문자열은 다음과 같은 과정으로 만들어진다.

1. X는 맨 처음에 "0"으로 시작한다.

2. X에서 0을 1로, 1을 0으로 뒤바꾼 문자열 X'을 만든다.

3. X의 뒤에 X'를 붙인 문자열을 X로 다시 정의한다.

4. 2~3의 과정을 무한히 반복한다.
   즉, X는 처음에 "0"으로 시작하여 "01"이 되고, "0110"이 되고, "01101001"이 되고, ⋯ 의 과정을 거쳐 다음과 같이 나타내어진다.

   "011010011001011010010110011010011001011001101001⋯⋯"

자연수 k가 주어졌을 때 X의 k번째에는 무슨 문자가 오는지 구하여라.

입력

첫 번째 줄에 자연수 k (1 ≤ k ≤ 1018) 가 주어진다.

출력

첫 번째 줄에 k번째에 오는 문자를 출력하라.

예제

조건

• 시간 제한: 1초
• 메모리 제한: 256MB

초기 코드

import sys
input = sys.stdin.readline 

# 입력
k = int(input())

# 예외 처리
if k == 1:
    print(0)
    exit(0)
elif k == 2:
    print(1)
    exit(0)

# 범위 지정    
n = 0  
while k > n**2:
    n += 1

# x 구하기
x = '01'
x_ ,pre_x= '1','0'
for i in range(2,n+1):
    if i % 2 == 0: # 현재 x의 길이가 2의 짝수 제곱일 경우
        x_ = x[::-1]
        pre_x = x  # 변경 전 상태를 저장
        x += x_    # 변경
        
    else:          # 현재 x의 길이가 2의 홀수 제곱일 경우
        x_ = x_ + pre_x  # x' = 직전 x' + 직전 x
        x += x_    # 변경
 
# 출력       
print(x[k-1])

처음에는 이런식으로 나름의 패턴을 발견해 작성을 해주었는데.. 메모리 제한이 떴다. 그래서 알아본 결과 투에-모스 수열의 점화식을 이용해 풀어야한다는 걸 알게 되었다.

투에-모스 수열? 🤔

• 0에서 시작해서 앞의 수열의 역순을 덧붙여서 얻어지는 이진 수열 (0과 1의 무한수열)이다.

• 0 => 0 + 1 => 01 + 10 => 0110 + 1001 ...

점화식

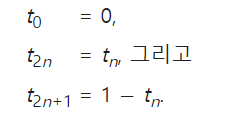
코드

import sys
input = sys.stdin.readline 

# 입력
k = int(input())

def Thue_Morse(x):
    if x == 0:
        return 0
    elif x == 1:
        return 1
    elif x % 2 == 0:
        return Thue_Morse(x//2)
    else:
        return 1 - Thue_Morse(x//2)
    
print(Thue_Morse(k-1))

1. k번째이기 때문에, k-1 로 넣어준다.

2. 7번째 숫자를 구하고 싶다고 가정해보자.

• Thue_Morse 함수에 k-1 인 6이 들어간다.

• 현재 x 는 6이므로, 짝수에 해당되어 Thue_Morse(x//2) 로 return 한다.

• 그 다음 x 는 3이므로, 홀수에 해당되어 1 - Thue_Morse(x//2) 로 return 한다.

• 3//2는 1로, x 가 1이므로, 1을 return 한다.

• x 가 3일 경우에 1을 return 받았으므로, 1-1인 0을 return 한다.

• 마지막으로 x 가 6일 경우에 0을 return 받았으므로, 0을 그대로 return 해주고 정답을 출력해준다.

느낀 점 & 배운 점

1. 투에-모스 수열이라는 다소 생소하지만 새로운 개념을 배우게 되었다. 알아둬서 나쁠 건 없을 듯하다.

2. 점화식만 알면 재귀함수로 쉽게 구할 수 있으니, 점화식을 구하는 방법도 잘 생각해보면 좋겠다!