[Python] S1_1074_Z ♒️

https://www.acmicpc.net/problem/1074

문제

한수는 크기가 2^N × 2^N인 2차원 배열을 Z모양으로 탐색하려고 한다. 예를 들어, 2×2배열을 왼쪽 위칸, 오른쪽 위칸, 왼쪽 아래칸, 오른쪽 아래칸 순서대로 방문하면 Z모양이다.

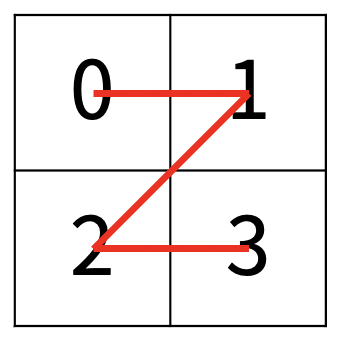
N이 주어졌을 때, r행 c열을 몇 번째로 방문하는지 출력하는 프로그램을 작성하시오.

입력

첫째 줄에 정수 N, r, c가 주어진다.

출력

r행 c열을 몇 번째로 방문했는지 출력한다.

조건

• 1 ≤ N ≤ 15
• 0 ≤ r, c < 2^N
• 시간 제한 0.5초
• 메모리 제한 512MB

접근

1. 우선 패턴을 파악해보자.
2. 언제 행과 열을 바꾸는지를 알아낸 후 코드에 적용시켜보자.
3. 무식하게 하나씩 짜보기...

🔔 이렇게 하다보니 당연히 N이 커지게 될 때마다 오류가 발생했고, 수정을 하면 할수록 끝없는 오류 지옥에 빠졌다...

이대로는 답이 없겠다 싶어서 구글링을 해본 결과
분할 정복 알고리즘 (Divide and Conquer Algorithm)을 알게 되었다.

Divide and Conquer Algorithm? 🔢

문제를 더 이상 분할할 수 없을 때까지 동일한 유형의 하위 문제로 나눈 후에 원하는 답을 찾아내는 알고리즘이다.

모든 경우를 완전 탐색하는 것이 아니라, 분할하면서 효율성을 증대시킨다는 점에서 이진 탐색 알고리즘 (binary search algorithm) 과 유사한 것 같기도 하다.

이러한 알고리즘의 적용과 어떤 분이 짜 놓으신 훌륭한 코드를 참고하여 다음과 같은 코드를 작성하였다.

코드

import sys
input = sys.stdin.readline

N,r,c = map(int,input().rstrip().split())

# Divide and Conquer Algorithm
answer = 0                      
while N>0:
    N -= 1
    
    # <1사분면>
    if r < 2**N and c < 2**N:
        answer += (2**N) * (2**N) * 0
    # <2사분면>
    elif r < 2**N and c >= 2**N:
        answer += (2**N) * (2**N) * 1
        c -= (2**N)
    # <3사분면>
    elif r >= 2**N and c < 2**N:
        answer += (2**N) * (2**N) * 2
        r -= (2**N)
    # <4사분면>
    else:
        answer += (2**N) * (2**N) * 3
        r -= (2**N)
        c -= (2**N)
        
print(answer)

코드만 보면 잘 이해가 되지 않기 때문에, 예제 문제인 N=3, r=7, c=7 일 경우로 생각해보겠다.

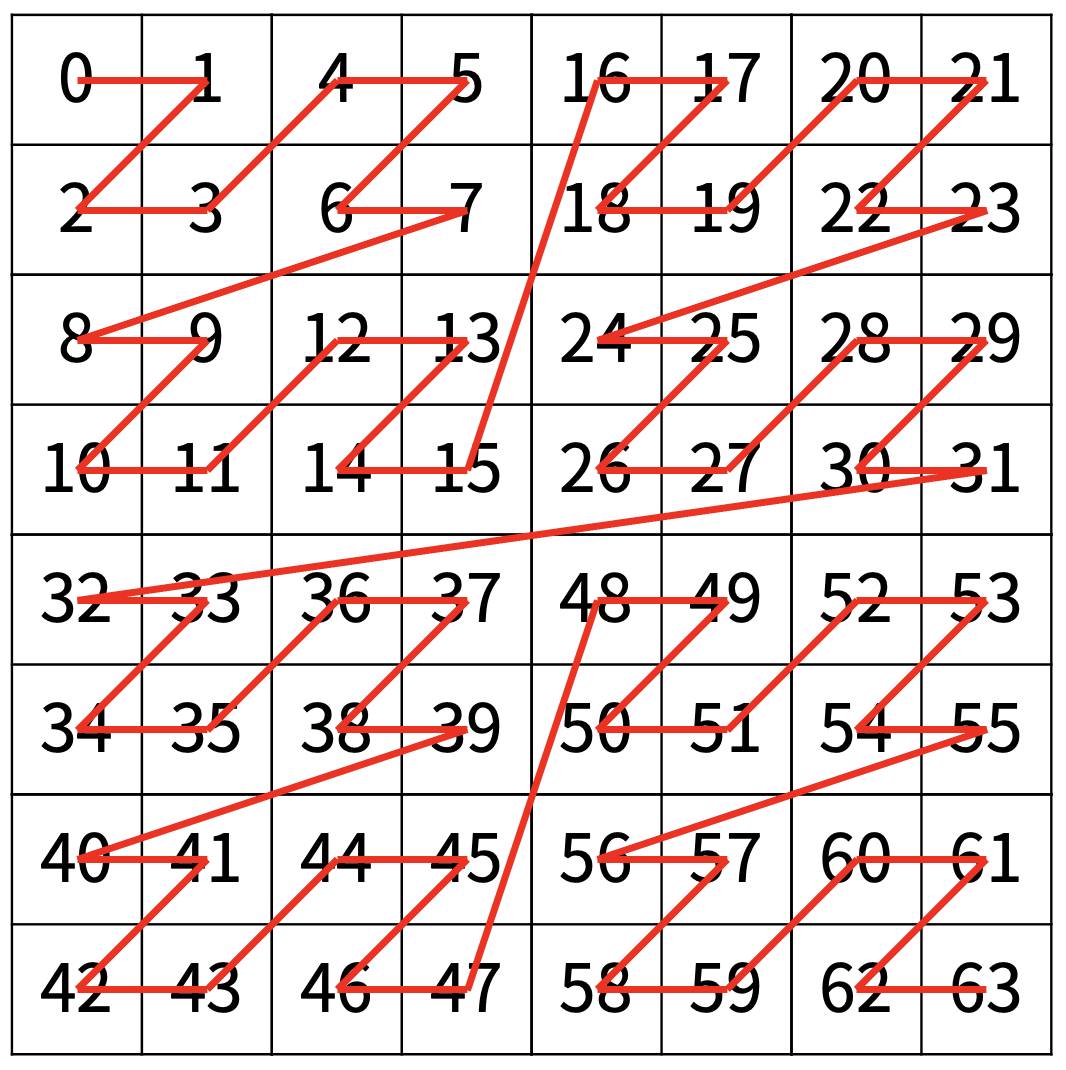
N이 3일 때는 다음과 같은 형태로 나타나며, 2^(N-1) × 2^(N-1)로 4등분 한 후에 재귀적으로 순서대로 방문한다.

즉 8x8의 형태이기 때문에, 4x4의 형태가 4개가 나오게 되며 이를 이제부터 좌측 위부터 1,2,3,4분면이라고 칭하겠다.

• 1사분면: 0부터 시작하며, [0,0] ~ [3,3]까지 존재한다.
• 2사분면: 16부터 시작하며, [0,4] ~ [3,7]까지 존재한다.
• 3사분면: 32부터 시작하며, [4,0] ~ [7,3]까지 존재한다.
• 4사분면: 48부터 시작하며, [4,4] ~ [7,7]까지 존재한다.

r과 c가 [7,7] 이기 때문에 4사분면에 해당하고, 필요없는 나머지 1,2,3 사분면은 버리게 된다.

시작점이 48이고 시작 인덱스가 [4,4]이었기 때문에,
answer += 48, r -= 4, c-= 4를 해준다.

현재 answer = 48, r = 3, c = 3, N = 2

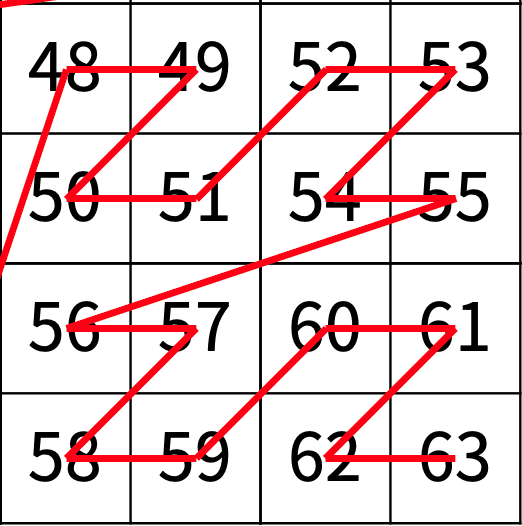
그럼 이와 같은 4x4의 형태가 나오게 되고, 2x2를 기준으로 다시 1,2,3,4분면으로 나눌 수 있게 된다.

위와 동일한 작업을 진행하게 되면, r과 c의 값인 [3,3]이 4사분면에 해당함을 할 수 있다.

1,2,3사분면은 버리면서 12개를 버리게 되니 answer += 12를 해주고, r -= 2, c -=2를 해준다.

현재 answer = 60, r = 1, c = 1, N = 1

마지막으로 N이 1이므로, 다음과 같이 2x2의 형태를 띄게 되고, 2^(N-1) = 2^0 = 1이므로 1x1 4개로 1,2,3,4분면이 나뉘게 된다.

여기서 [1,1]은 4사분면에 해당하므로, 3개를 버리게 되면서 answer += 3, r -= 1, c-= 1을 해준다.

현재 answer = 63, r = 0, c = 0, N = 0

N이 0이 되었기에 더 이상 분할할 수 없음을 의미하고, 지금까지 더해진 answer값을 출력한 후 종료한다.

느낀 점 & 배운 점

1. 딱 보았을 때 규칙이 있는 것은 생각보다 간단하게 코드를 짤 수가 있다. 이제 무식하게 짜려하지 말고, 패턴을 파악해보자.

2. 분할 정복 알고리즘에 대해서 배워보았다. 앞으로 여러 방향으로 응용해서 유용하게 쓸 수 있을 것 같으니 잊지 말고 기억해두자!

3. 이진 탐색, 분할 정복 등을 공부하다 보니 자료구조와 알고리즘 공부를 하는 것이, 데이터를 효율적으로 정렬하고 탐색하고 접근하는 데 필수적이라는 생각이 들었다.

4. 어떻게 하면 더 빨리, 불필요한 작업 없이 목표에 도달할 수 있는지를 고민하는 게 중요한 것 같다. 물론 오류는 최소화하면서 말이다.