내배캠 두 번째 팀 프로젝트

🗓️ 프로젝트 기간 🗓️

7월 9일부터 7월 21일까지

---

📖 오늘의 내가 한 일 📖

로얄티 멤버십 효과

• 가설: 멤버십을 가입한 고객은 미가입 고객보다 고객 생애 가치가 높다.
• 가설: 멤버십을 가입한 고객은 미가입 고객보다 재구매률이 높다.

---

#고객 정보 = 고객별 주문 수, CLV, 멤버십 정보 집계
customer_info = SSE.groupby('Customer ID').agg(repurchase_count = ('Total Purchase Amount','count'),
                                               CLV              = ('Total Purchase Amount','sum'),
                                               Loyalty          = ('Loyalty Member','first')).reset_index()

customer_info

[결과 값]

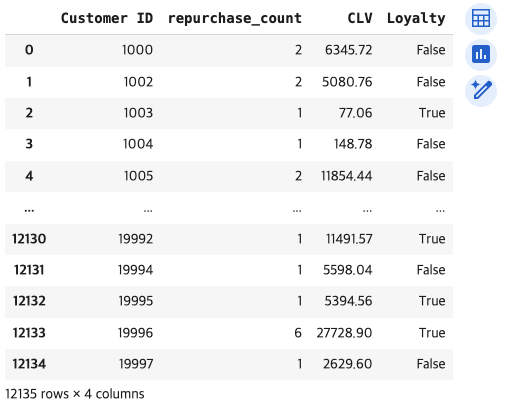
#재구매(기준 2번 이상 구매한 고객)값 확인하기
customer_info['repeat_purchase'] = customer_info['repurchase_count'] > 1
customer_info['repeat_purchase'].value_counts()

[결과 값]

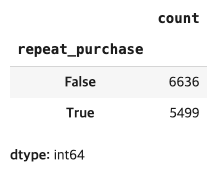
#멤버십 가입 기준 재구매율
customer_info.groupby('Loyalty').agg(repurchase_rate = ('repeat_purchase','mean'),
                                      avg_CLV        = ('CLV','mean'),
                                      cnt_c          = ('CLV','count')).reset_index()

[결과 값]

---

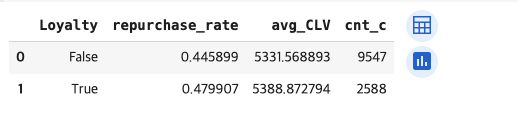
t검정 결과

#t검정(CLV 연속형 데이터와 멤버십 가입여부 범주형 데이터의 비교)

group_T = customer_info.loc[customer_info['Loyalty']==True, 'CLV'] #멤버십 가입한 고객
group_F = customer_info.loc[customer_info['Loyalty']==False,'CLV'] #멤버십 가입 안한 고객
stat, p_value = ttest_ind(group_T, group_F, equal_var=False)
print(f"CLV t-test → statistic: {stat:.3f}, p-value: {p_value:.3f}")

#t검정 결과: 멤버십 가입한 고객과 멤버십 가입 안한 고객의 CLV 평균 차이가 통계적으로 유의미 하지 않다. 귀무가설 채택

[결과 값]

---

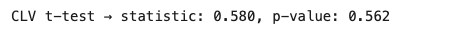
추가 의문

멤버십 가입 여부(범주형)과 재구매율(비율/확률) 비교

from statsmodels.stats.proportion import proportions_ztest

# 1) 재구매 플래그(is_repeat) 추가
customer_info['is_repeat'] = customer_info['repurchase_count'] > 1

# 2) 그룹별 재구매 수와 총 고객 수 집계
grouped = (
    customer_info
      .groupby('Loyalty')['is_repeat']
      .agg(repeat_count='sum',  # 재구매 고객 수
           total_count='count') # 전체 고객 수
      .reset_index()
)
# 재구매율 컬럼 추가
grouped['repurchase_rate'] = grouped['repeat_count'] / grouped['total_count']

print(grouped)
# 예시 출력
#    Loyalty  repeat_count  total_count  repurchase_rate
# 0    False          4262         9547         0.446
# 1     True          1242         2588         0.480

# 3) proportion z-test 실행
count = grouped['repeat_count'].values      # [재구매_False, 재구매_True]
nobs  = grouped['total_count'].values       # [전체_False, 전체_True]
stat, pval = proportions_ztest(count=count, nobs=nobs)

print(f"proportion z-test → statistic: {stat:.3f}, p-value: {pval:.3f}")

[결과 값]

결론:

1. 멤버십 가입 여부와 CLV는 통계적으로 유의미한 관계가 없다.(p-value 0.562) = 귀무가설 채택

2. 멤버십 가입 여부와 재구매율은 통계적으로 유의미한 관계가 있다. = 귀무가설 기각, 대립가설 채택
   (p-value 0.002)

2번 가설은 발전의 가능성이 있다.