통계학 라이브 세션(1)

라라·2025년 6월 25일

통계학 시리즈

목록 보기

1/5

데이터의 종류

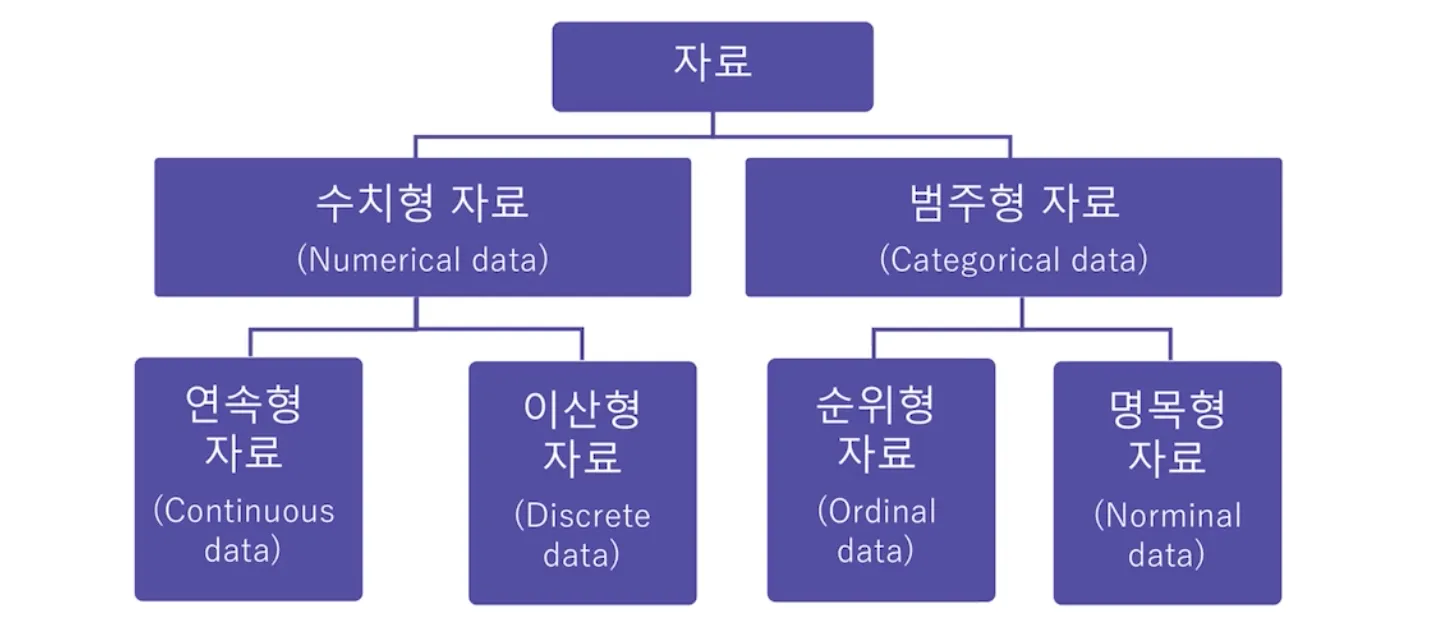
데이터 분석에 사용되는 통계

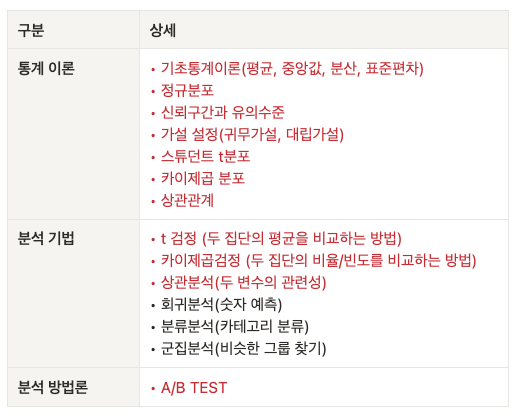
데이터 종류

수치형 : 숫자를 이용해 표현할 수 있는 데이터
- 연속형
  - 일정 범위 안에서 어떤 값이든 취할 수 있는 데이터
    - 체중, 신장
- 이산형
  - 횟수와 값은 정수형 값만 취할 수 있는 데이터
    - 소수점의 의미가 없는 데이터를 의미
      - 사고건수, 일 방문자 수
범주형 : 가능한 범주 안의 값만을 취하는 데이터
- 이진형
  - 두 개의 값만을 가지는 범주형 데이터의 특수한 경우
    - 성공 여부, 0과 1, 예 or 아니오, 참 or 거짓
- 순서형
  - 값들 사이에 분명한 순위가 있는 데이터
    - 등수

❓데이터의 종류를 분류해야하는 이유❓

1️⃣ 데이터의 생김새가 시각화, 해석, 통계 모델 결정에 중요한 역할

2️⃣ 마케터는 데이터의 종류를 이해하고 관련분석을 어떻게 수행할 지 결정

편차, 분산, 표준편차, 표본분포

✅ 데이터의 대표 값 : 평균, 중앙값, 최빈값

➡️ 평균: 모든 값의 총 합을 개수로 나눈 값
➡️ 중간값 : 데이터 중 가운데 위치한 값
➡️ 최빈값 : 데이터 중 가장 많이 도출된 값

⭐️ 편차 : 각 점수가 평균에서 얼마나 떨어져 있는지를 계산한 값
✅ 편차 = 점수 - 평균

⭐️ 분산 : 편차의 합이 0으로 나오는 것을 방지하기 위해 생성된 개념
✅ 편차를 제곱해서 평균낸 값

⭐️ 표준편차(standard deviation) : 분산의 제곱근
✅ 분산은 단위가 제곱이라서 해석이 어렵지만 표준편차는 원래 단위로 다시 바꿔줌

▶️ 모집단 : 조사하고 싶은 전체 대상

▶️ 표본 : 모집단에서 일부만 뽑은 집단

▶️ 표본평균 : 뽑은 표본의 평균 값

▶️ 표본분표 : 표본의 분포(표본이 흩어져 있는 정도)

▶️ 표본평균의 분포 : 여러 표본의 평균을 모아 만든 분포
➡️ 데이터가 충분한 경우 정규분포를 따름 = 중심극한정리

❗️정규분포 란?

▶️ 표준오차 : 표본의 표준편차 = 표본평균의 평균과 모평균의 차이

표본이 많을 수록 표준 오차는 작아짐

도수분포표

모집단에서 표본을 추출하고, 이를 시각화하여 통계적 의미를 찾는 것도 중요

이 과정에서 아래 개념들을 이해해야 하며 이해한 개념을 바탕으로 심화프로젝트에서 통계적 해석을 진행

도수: 특정 구간에 발생한 값의 수
상대도수: 특정 도수를 전체 도수로 나눈 비율
도수분포표: 각 값에 대한 도수와 상대도수를 나타내는 표
히스토그램: 도수분포표를 활용하여 만든 막대그래프
임의표본추출: 무작위로 표본을 추출하는 것
편향: 한쪽으로 치우쳐져 있음
도수분포표 만들기

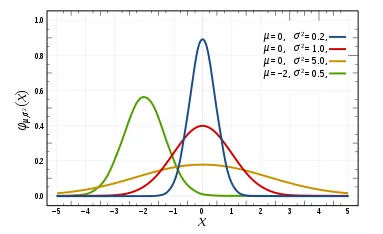
정규분포의 특징

분포는 평균을 중심으로 좌우 대칭의 형태
곡선은 각 확률값을 나타내며, 모두 더하면 1이 됨
(동전을 뒤집어서 앞면이 나올 확률은 2분의 1 + 뒷면이 나올 확률 2분의 1 = 전체 확률 1)
정규분포는 평균과 분산(퍼진정도)에 따라 다른 형태를 가짐
평균 0, 분산 1을 가지는 경우, 이를 표준정규분포라고 합니다. (그림의 붉은색 그래프)

신뢰구간, 신뢰수준

모든 데이터는 표본을 추출하는 순간 불확실성을 가짐

모집단 전체를 사용하지 않는 한, 결과가 한끗차이도 나지 않기는 어렵다! 라는 의미

이러한 데이터의 불확실성을 우리는 ‘신뢰도’ 이라는 개념으로 약속

신뢰구간: 특정 범위 내에 값이 존재할것으로 예측되는 영역
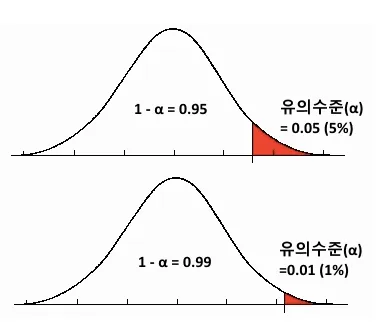
신뢰수준: 실제 모수를 추정하는데 몇 퍼센트의 확률로 신뢰구간이 실제 모수를 포함하게 되는 확률. 주로 95%와 99% 를 이용합니다.
- 신뢰수준 95% :무작위로 표본을 추출했을 때, 100번 중 95번은 신뢰구간 안에 모집단의 값을 포함
- 신뢰수준 99% : 무작위로 표본을 추출했을 때, 100번 중 99번은 신뢰구간 안에 모집단의 값을 포함
주의점
- 신뢰수준이 높아지게 되면 → 신뢰구간이 넓어지지만 → 정확한 예측이 어렵기 때문에, 95% 신뢰수준보다 99% 신뢰수준이 좋다고 할 수 없음

👉 python 라이브러리 중 하나인 scipy 를 활용하여 95% 와 99% 신뢰구간을 구현

import scipy.stats as st
import numpy as np

#샘플 데이터 선언 
sample1 = [5, 10, 17, 29, 14, 25, 16, 13, 9, 17]
sample2 = [21, 22, 27, 19, 23, 24, 20, 26, 25, 23]

# 신뢰구간을 구할때는 일반적으로 표준오차를 사용해줍니다. 
# 표준 편차: 각 값이 평균으로부터 떨어진 정도 
# 표준 오차: 표본 평균이 '진짜 평균'에서 얼마나 떨어져있는지
# 즉, 표준편차를 통해 각 값이 평균으로부터 얼마나 떨어져 있는 지 파악한 후, 
# 표준오차를 통해 표본의 평균이 어느정도로 정확하게 모집단의 평균을 추정하는지를 나타내주게 됩니다. 
# 이는 곧 신뢰구간을 구하는 것이 되겠습니다. 

df = len(sample1) - 1 # 자유도 : 샘플 개수 - 1
mu = np.mean(sample1) # 표본 평균
se = st.sem(sample1) # 표준 오차

# 95% 신뢰구간
st.t.interval(0.95, df, mu, se) # (10.338733110887336, 20.661266889112664)

# 99% 신뢰구간
st.t.interval(0.99, df, mu, se) # (8.085277068873378, 22.914722931126622)