[파이썬 알고리즘] 우선순위큐(priority) & 힙큐(heap)

신현식·2023년 6월 7일

파이썬알고리즘

목록 보기

3/4

스택(Stack) 과 큐(Queue)

큐 (queue) 는 컴퓨터의 기본적인 자료 구조의 한가지로, 먼저 집어넣은 데이터가 먼저 나오는 FIFO 구조로 저장하는 형식을 말한다. 우선순위 큐는 우선순위의 개념을 큐에 도입한 자료구조로, 데이터들이 우선순위를 가지고 있고 우선순위가 높은 데이터가 먼저 나가는 자료구조를 말한다.

우선순위 큐는 배열, 연결리스트, 힙으로 구현이 가능하다. 이 중에서 힙(heap)으로 구현하는 것이 가장 효율적이다.
- 배열과 연결리스트는 선형 구조의 자료구조이므로 삽입 또는 삭제 연산을 위한 시간복잡도는 O(n)이다.
- 반면 힙트리는 완전이진트리 구조이므로 힙트리의 높이는 log₂(n+1)이며, 힙의 시간복잡도는 O(log₂n)이다.

Priority Queue 와 Heaq의 차이

queue 속 PriorityQueue 는 Thread-Safe 하고 heapq는 Non-safe 하기 때문이라고 한다.
Thread Safe 하다는 것은 반드시 확인 절차를 걸쳐야 하기 때문에 확인하는 작업떄문에 더 느리다.

Thread-Safe를 요구하는 상황에서는 PriorityQueue
Thread-Non-Safe 해도 된다면 heapq

코딩테스트로 문제를 푸는 상황이라면 Thread-Safe를 요구하지 않기 때문에 heapq를 써야 시간초과를 면할 수 있을 것이다. 실무에서도 우선순위 큐는 대부분 heapq로 구현하고 있다.

힙(heap)

힙 (heap) 은 최댓값 및 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안된 완전이진트리를 기본으로 한 자료구조이다.

A가 B의 부모노드이면, A의 key값과 B의 key값 사이에는 대소관계가 성립한다.(반정렬 상태)
키 값의 대소 관계는 부모/자식 간에만 성립하고, 형제노드 사이에는 대소 관계가 정해지지 않는다.
이진탐색트리(BST)와 달리 중복된 값이 허용된다.

힙에는 '최대 힙' 과 '최소 힙' 이 있다.

최대 힙 : 부모 노드의 키 값이 자식 노드보다 크거나 같은 완전이진트리이다.
❝ key(부모노드) ≥ key(자식노드) ❞
최소 힙 : 부모 노드의 키 값이 자식 노드보다 작거나 같은 완전이진트리이다.
❝ key(부모노드) ≥ key(자식노드) ❞

힙은 가장 높은(혹은 가장 낮은) 우선순위를 가지는 노드가 항상 루트노트에 오게되는 특징이 있으며, 이를 응용하면 우선순위 큐와 같은 추상적 자료형을 구현할 수 있다.

힙(heap)의 구현

힙은 일반적으로 배열을 이용하여 구현한다. 완전 이진트리이므로 중간에 비어있는 요소가 없기 때문이다.

구현을 쉽게 하기 위해 배열의 첫번째 인덱스인 0은 사용되지 않는다.
특정위치의 노드번호는 새로운 노드가 추가되어도 변하지 않는다.
- 예를 들어 루트노드의 오른쪽 노드 번호는 항상 3이다.

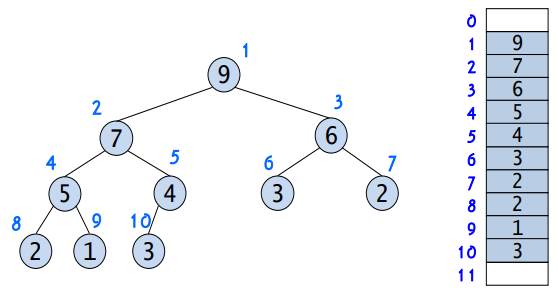
트리의 각 노드에 번호를 붙이고, 이 번호를 배열의 인덱스로 생각하면 효과적으로 힙을 구현할 수 있다. 배열로 구현하였기 때문에 부모 또는 자식 노드를 찾아가는 연산을 구현하기도 간편하다.

힙에서의 부모노드와 자식노드의 관계
- 왼쪽 자식의 인덱스 = (부모의 인덱스) * 2
- 오른쪽 자식의 인덱스 = (부모의 인덱스) * 2 + 1
- 부모의 인덱스 = (자식의 인덱스) / 2

힙의 삽입 : 새로운 요소를 마지막 노드에 이어서 삽입 후, 힙의 성질 만족할 때까지 부모노드와 교환
최악의 경우 새로 추가된 노드가 루트노트까지 비교하며 올라가야 하므로 시간복잡도가 O(log₂n)이다.
힙의 삭제 : (최대 힙의 경우) 루트 노드 삭제 후 마지막 노드를 루트 노드에 위치 시킨 뒤 힙의 성질 만족할 때 까지 자식노드와 교환
삭제 연산 또한 최악의 경우 루트노트부터 가장 아래까지 내려가야 하므로 시간복잡도가 O(log₂n)이다.

파이썬 힙 자료구조

파이썬 heapq 모듈은 완전 이진트리 기반의 최소 힙 자료구조이다. 즉 루트노드는 heapq에서 가장 작은 값이다.

heapq.heappush(heap, item) : item을 heap 에 추가

import heapq

heap_list = []
heapq.heappush(heap_list, 5)
heapq.heappush(heap_list, 10)
heapq.heappush(heap_list, 99)
heapq.heappush(heap_list, 2)

print(heap_list) # [2, 5, 99, 10]

heapq.heappop(heap) : heap에서 가장 작은 원소를 pop & 리턴, 비어있는 경우 IndexError 호출

print(heapq.heappop(heap_list))  # 2
print(heap_list)  # [5, 10, 99] 
a = heapq.heappop(heap_list)
print(a)  # 5

heapq.heapify(x) : 리스트 x 를 즉각적으로 heap 으로 변환함 (in linear time, O(N))

import heapq

h = [ [4, "fourth"], [2, "second"], [3, "third"], [1, "first"]]
heapq.heapify(h)
print(h)

#[[1, 'first'], [2, 'second'], [3, 'third'], [4, 'fourth']]

최대 힙 만들기

힙에 원소를 추가할때 튜플 형태로 넣어주면 튜플의 첫 번째 원소를 우선순위로 힙을 구성하게 된다는 아이디어를 이용한다.

(-item, item) 의 튜플 형태로 push 하는 경우 제일 큰 값이 루트노드에 위치하는 최대 힙을 만들 수 있다.

heap_items = [1,3,5,7,9]

max_heap = []
for item in heap_items:
  heapq.heappush(max_heap, (-item, item))

print(max_heap)

-> [(-9,9), (-7,7), (-5,5), (-3,3), (-1,1)]

heappop을 사용하면 가장 앞에 있는 최댓값이 반환되는 것을 확인할 수 있다. 이 때 실제 원소값은 튜플의 두번째 자리에 저장되어 있다.

max_item = heapq.heappop(max_heap)[1]

신현식

전공 소개

[파이썬 알고리즘] 우선순위큐(priority) & 힙큐(heap)