프로그래머스 - 카드 짝 맞추기 (2021 카카오 블라인드 공채)

정답률 0.95퍼의 무시무시한 문제다.

문제 제목

카드 짝 맞추기

문제 설명

게임 개발자인 베로니는 개발 연습을 위해 다음과 같은 간단한 카드 짝맞추기 보드 게임을 개발해 보려고 합니다.
게임이 시작되면 화면에는 카드 16장이 뒷면을 위로하여 4 x 4 크기의 격자 형태로 표시되어 있습니다. 각 카드의 앞면에는 카카오프렌즈 캐릭터 그림이 그려져 있으며, 8가지의 캐릭터 그림이 그려진 카드가 각기 2장씩 화면에 무작위로 배치되어 있습니다.
유저가 카드를 2장 선택하여 앞면으로 뒤집었을 때 같은 그림이 그려진 카드면 해당 카드는 게임 화면에서 사라지며, 같은 그림이 아니라면 원래 상태로 뒷면이 보이도록 뒤집힙니다. 이와 같은 방법으로 모든 카드를 화면에서 사라지게 하면 게임이 종료됩니다.

게임에서 카드를 선택하는 방법은 다음과 같습니다.

• 카드는 커서를 이용해서 선택할 수 있습니다.
  커서는 4 x 4 화면에서 유저가 선택한 현재 위치를 표시하는 "굵고 빨간 테두리 상자"를 의미합니다.
• 커서는 [Ctrl] 키와 방향키에 의해 이동되며 키 조작법은 다음과 같습니다.
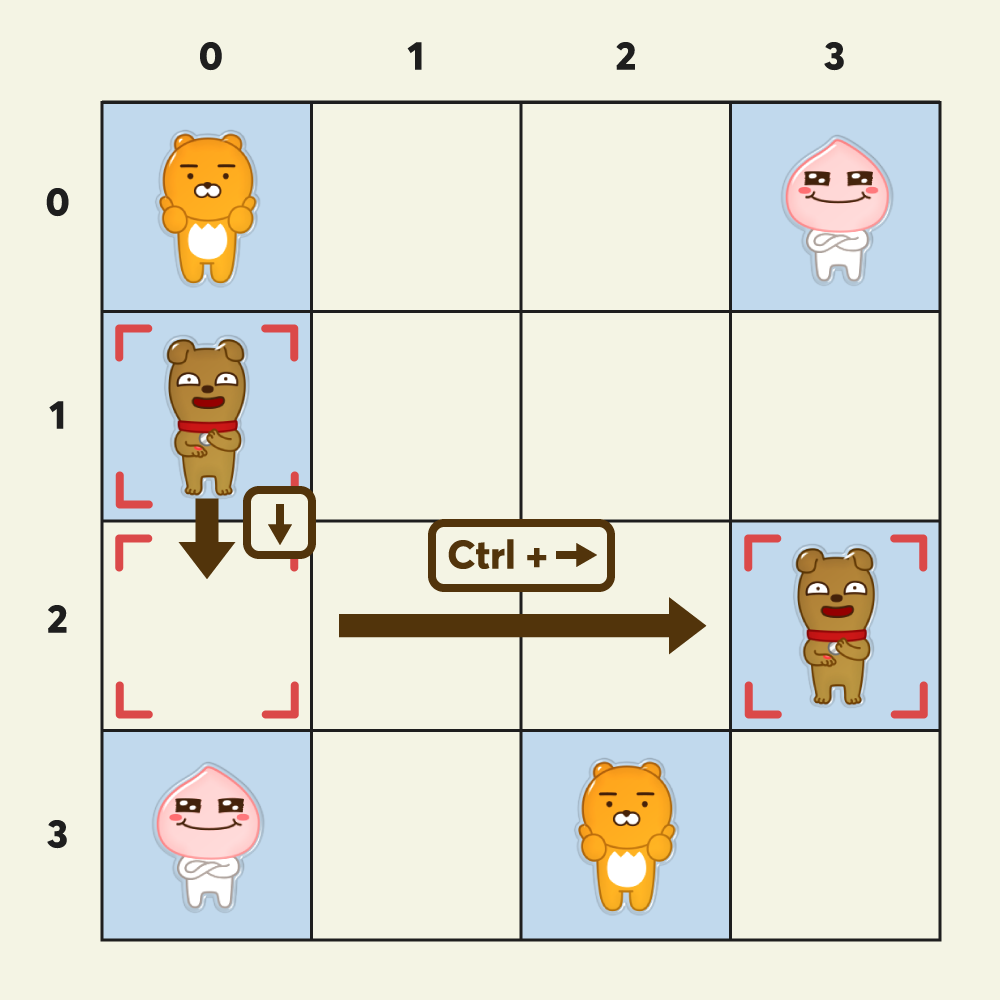
  방향키 ←, ↑, ↓, → 중 하나를 누르면, 커서가 누른 키 방향으로 1칸 이동합니다.
  [Ctrl] 키를 누른 상태에서 방향키 ←, ↑, ↓, → 중 하나를 누르면, 누른 키 방향에 있는 가장 가까운 카드로 한번에 이동합니다.
  만약, 해당 방향에 카드가 하나도 없다면 그 방향의 가장 마지막 칸으로 이동합니다.
  만약, 누른 키 방향으로 이동 가능한 카드 또는 빈 공간이 없어 이동할 수 없다면 커서는 움직이지 않습니다.
• 커서가 위치한 카드를 뒤집기 위해서는 [Enter] 키를 입력합니다.
  [Enter] 키를 입력해서 카드를 뒤집었을 때 앞면이 보이는 카드가 1장 뿐이라면 그림을 맞출 수 없으므로 두번째 카드를 뒤집을 때 까지 앞면을 유지합니다.
  앞면이 보이는 카드가 2장이 된 경우, 두개의 카드에 그려진 그림이 같으면 해당 카드들이 화면에서 사라지며, 그림이 다르다면 두 카드 모두 뒷면이 보이도록 다시 뒤집힙니다.
  "베로니"는 게임 진행 중 카드의 짝을 맞춰 몇 장 제거된 상태에서 카드 앞면의 그림을 알고 있다면, 남은 카드를 모두 제거하는데 필요한 키 조작 횟수의 최솟값을 구해 보려고 합니다. 키 조작 횟수는 방향키와 [Enter] 키를 누르는 동작을 각각 조작 횟수 1로 계산하며, [Ctrl] 키와 방향키를 함께 누르는 동작 또한 조작 횟수 1로 계산합니다.

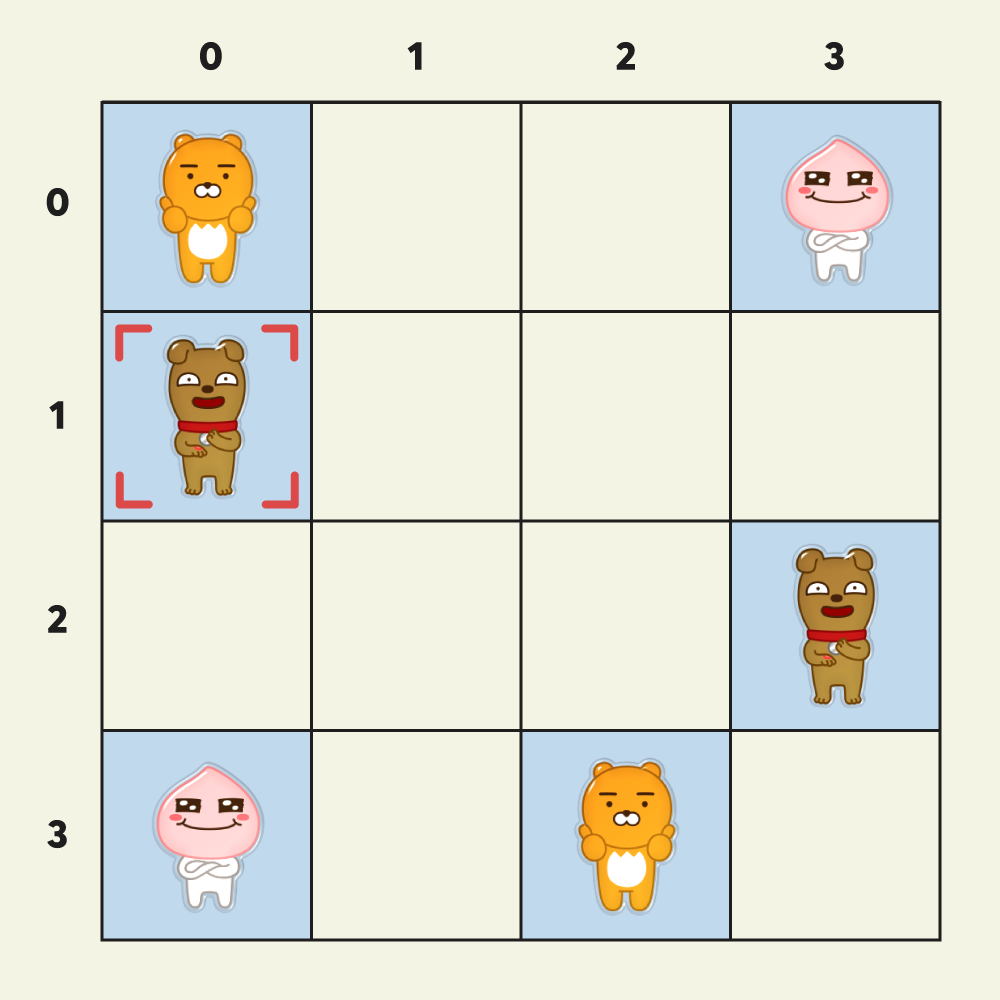
다음은 카드가 몇 장 제거된 상태의 게임 화면에서 커서를 이동하는 예시입니다.
아래 그림에서 빈 칸은 이미 카드가 제거되어 없어진 칸을 의미하며, 그림이 그려진 칸은 카드 앞 면에 그려진 그림을 나타냅니다.

<예시는 생략하겠습니다.>

문제

현재 카드가 놓인 상태를 나타내는 2차원 배열 board와 커서의 처음 위치 r, c가 매개변수로 주어질 때, 모든 카드를 제거하기 위한 키 조작 횟수의 최솟값을 return 하도록 solution 함수를 완성해 주세요.

제한 사항

• board는 4 x 4 크기의 2차원 배열입니다.
• board 배열의 각 원소는 0 이상 6 이하인 자연수입니다.
• 0은 카드가 제거된 빈 칸을 나타냅니다.
• 1 부터 6까지의 자연수는 2개씩 들어있으며 같은 숫자는 같은 그림의 카드를 의미합니다.
• 뒤집을 카드가 없는 경우(board의 모든 원소가 0인 경우)는 입력으로 주어지지 않습니다.
• r은 커서의 최초 세로(행) 위치를 의미합니다.
• c는 커서의 최초 가로(열) 위치를 의미합니다.
• r과 c는 0 이상 3 이하인 정수입니다.
• 게임 화면의 좌측 상단이 (0, 0), 우측 하단이 (3, 3) 입니다.

예제 입출력

입력

board : [[1,0,0,3],[2,0,0,0],[0,0,0,2],[3,0,1,0]]
r : 1
c: 0

board : [[3,0,0,2],[0,0,1,0],[0,1,0,0],[2,0,0,3]]	
r : 0
c: 1

출력

14
16

입출력 예 #2

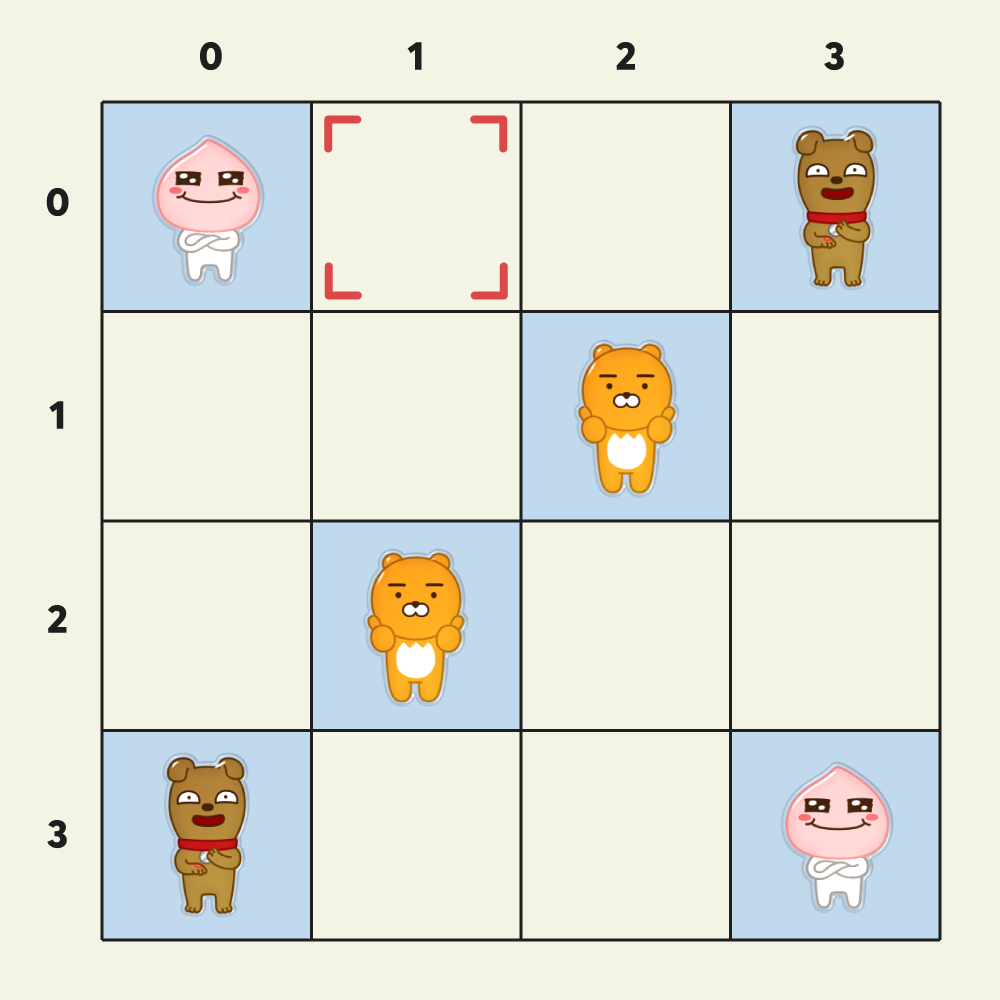
위 게임 화면에서 모든 카드를 제거하기 위한 키 조작 횟수의 최솟값은 16번 입니다.

풀이

문제를 읽으면서 이걸 도대체 어떻게? 라는 생각이 강하게 들었다. 그 이유는 아래와 같은데

1. 제약조건이 너무 많다. ctrl 이동이나 카드를 뒤집는 행동에서 코너케이스가 분명히 나올것 같았다.
2. 할 수 있는 행동이 너무 많다. 단순히 생각해보자. 커서를 기준으로 ←, ↑, ↓, → 이동과 ctrl + ←, ↑, ↓, → (엑셀에서의 그것) , 카드를 첫번째로 뒤집는 것, 카드를 뒤집은 상태에서 다시 뒤집는 것. 정말 많다.
3. 카드가 다 보이는 상태인가? 아니면 뒤집어 봐야지 아는건가?

사고의 과정

문제 독해를 다시 천천히 해보자. 그러면 아래와 같은 점때문에 풀 수 있어 보인다.

1. 2차원 격자가 4x4, 16칸으로 매우 매우 작다. 완전탐색이 가능해보인다.
2. 모두 뒤집혔을때의 키 조작 횟수의 최솟값을 묻고 있다.
3. 변화하는 상태의 개수를 명확하게 알 수 있다.

이쯤되면 한가지 풀이 밖에 없다. BFS다.

다만 구현할 부분이 매우 많은 BFS 풀이일뿐이다. 개인적인 생각으로 삼성 기출 문제를 열심히 공부하신 분들이라면 어렵지 않게 구현할 수 있을거라고 생각한다.

저는 삼성 기출문제 공부를 잘 안했습니다.

커서를 기준으로 생각하자.

일단 커서의 위치를 기점으로 가능한 행동을 나눠보자.

1. 단순히 커서를 격자에서 벗어나지 않게 상,하,좌,우로 움직인다.
2. 격자에서 벗어나지 않게 ctrl + 상,하,좌,우로 움직인다.
   • 카드가 있다면 카드로 이동한다.
   • 해당 방향에 카드가 없다면 맨 끝으로 이동한다.
3. Enter를 눌러 카드를 뒤집는다.
   • 이번이 처음 뒤집는 카드라면, 그 카드를 기록한다.
   • 이미 뒤집은 카드가 있다면, 그 카드와 지금 카드를 비교한다.
     1. 두 그림이 같으면 , 카드를 삭제한다.
     2. 다르면 , 뒤집어진 카드를 다시 뒤집는다.

정리해보면 생각보다 간단하다. 각각의 변화하는 상태를 그래프에서의 노드로 보고 위에서 적은 3가지 행동을 모두 하는 완전탐색을 수행한다. 이 과정에서 최소 횟수를 구하니 BFS다.

변화하는 상태

이제 생각할 건 하나다. 매 탐색마다 어떤것이 변화할까?

일단 커서가 매번 움직이니, 커서의 위치는 변한다. 또, 단순히 탐색하는것이 아니라 격자에 변화를 주기 때문에 격자의 상태가 변화한다.

여기까지는 일반적이다. 그럼 이 문제에서 특수한 상황은 카드를 뒤집는 행동이다.

• 이번이 처음 뒤집는 카드라면, 그 카드를 기록한다.
• 이미 뒤집은 카드가 있다면, 그 카드와 지금 카드를 비교한다.

그러면 현재 카드를 뒤집었는지(False=0 or True=1장 뒤집었는지) 와 카드를 뒤집었다면 뒤집은 카드의 위치 역시 변한다.

단순히 변한다고만 해서 기록해줘야 하는 것은 아니다. 기록해줘야 하는 조건은 특정 조건이 없을때 탐색을 생략한다거나 중복으로 탐색하게 된다면, 그 특정 조건은 필요한 것이다.

예를 들어보자.
Enter 행동은 카드를 뒤집는 행동이다. 카드를 뒤집는것을 기록을 해주지 않는다면, visit 배열 안에 뒤집기 전의 상태가 그대로 들어가 있기 때문에, Enter 행동을 수행할 수 없다.

중복적인 탐색을 방지하는게 visit의 역할이기 때문이다.

정리하자면, 변화하는 상태는

1. 격자의 상태
2. 커서의 위치
3. 현재 카드를 0 or 1장 뒤집었는지
4. 카드를 뒤집었다면 뒤집은 카드의 위치
   • 3번이 True면 뒤집은 카드의 위치
   • 3번이 False면 (-1,-1)

구현 의사코드

위에서 적은 커서의 움직임과 변화하는 상태를 기반으로 코드를 작성해보자.
탐색 여부를 체크하는 visit은 변화하는 상태가 많기 때문에, 고차원 list로 구성하기가 곤란하다. set을 이용하되 복잡도에 유의하자.

visit=set()
q=deque()
visit.add(초기격자의 상태,커서의 위치,카드를 뒤집지 않음,(-1,-1))
q.add(초기격자의 상태,커서의 위치,카드를 뒤집지 않음,(-1,-1),조작 횟수)

while q:
	보드의 상태,기존 커서의 위치,카드를 뒤집었는지,뒤집었다면 위치,횟수=q.popleft()
    
    for 상,하,좌,우 네 방향으로 :
    	새 커서 위치=방향별로 한칸 움직인 좌표=기존 커서의 위치+1
        
        if 격자를 벗어났다면:
        	continue
        
        if 이전의 상태,새 커서 위치를 방문한적 있다면:
        	continue
        
        이전의 상태,새 커서 위치를 방문으로 표시
        이전의 상태,새 커서 위치,횟수+1를 다음에 탐색
        
    for 상,하,좌,우 네 방향으로 ctrl 이동 :
    	# 격자가 이렇고 C가 커서 일때 
        # 0 0 0 0 
        # 2 0 0 2 
        # 0 0 0 0 
        # 0 0 0 C 
        # 왼쪽으로 간다면 (0,3), 위로 간다면 (3,1)
    	새 커서 위치=min(기존 커서의 위치에서 방향별로 끝,존재하는 카드의 끝)
        
        if 이전의 상태,새 커서 위치를 방문한적 있다면:
        	continue
        
        이전의 상태,새 커서 위치를 방문으로 표시
        이전의 상태,새 커서 위치,횟수+1를 다음에 탐색
    
    # 현재 한장은 뒤집은 상태에서 다른것 뒤집으려 할때
    if 현재 카드를 뒤집은 상태라면 :
    	# 짝을 찾는데 성공
    	if 지금 위치의 카드와 이전에 뒤집었던 카드가 같다면:
            격자에서 현재 카드 숫자를 제거함
            
            if 지금 모든 카드를 제거했다면:
            	return 횟수+1
            else 아직 끝낼수 없다면:
            	바뀐 격자의 상태,현재 커서위치,뒤집지 않음을 방문으로 표시
                바뀐 격자의 상태,현재 커서위치,뒤집지 않음을 다음에 탐색                		
        # 짝 맞추기 실패 
        else 지금 위치의 카드와 이전에 뒤집었던 카드가 다르다면:
            이전 상태,현재 커서의 위치,뒤집지 않음을 방문으로 표시
            이전의 상태,현재 커서의 위치,카드를 뒤집음,횟수+1을 다음에 탐색
        
    else 카드를 하나도 안 뒤집은 상태라면 :
    
    	if 이전의 상태,카드를 뒤집음,현재 커서의 위치를 방문한적 있다면:
        	continue
        
        이전의 상태,현재 커서의 위치,카드를 뒤집음을 방문으로 표시
        이전의 상태,현재 커서의 위치,카드를 뒤집음,횟수+1를 다음에 탐색

구현이 꽤 복잡하지만 하나씩 보면, 커서의 행동별로 분류해서 전혀 복잡하지 않다. 신경써줄 부분은 ctrl+상,하,좌,우 이동에서 가까운 카드 혹은 끝 부분을 찾는 방법과 카드를 뒤집은 상태에서 카드 짝을 맞췄는지 아닌지 파악하는 부분이다.

구현에서의 몇가지 팁

다만 격자의 상태를 기록해야하는데, 탐색이 커지는 경우에는 매 탐색마다 deque에 4x4 격자를 넣기에는 메모리를 걱정해줘야할 수 있으니, 4x4 격자를 직렬화하는 방식을 택했다.

def serialize(board) -> str:
	ret = ''
        for r in board:
            for num in r:
                ret += str(num)

        return ret

이 경우에는 2차원 좌표인 (x,y) 접근이 아니라 1차원 idx 접근으로 해야하기 때문에 (x,y) -> idx로 변환해주는 함수가 필요하다.

def idxConverter(y:int, x:int) -> int:
        return 4 * y + x

이 경우에 훨씬 편리한점이 생기는데, 바로 카드를 제거할때 격자 안에 있는 요소를 변경하는 것이 아니라 string.replace() 함수를 사용할 수 있다.

 def switchTo0(s,num):
        return s.replace(num,'0')

해설과는 다른 풀이입니다.

2021 카카오 신입공채 문제해설의 6번 풀이를 보면 카드별로 지우는 순서를 순열로 정하고 순서대로 최단거리를 수행 후 최단거리의 합 중에서의 최소를 구하는데, 음.. 개인적인 생각으로 해설이 항상 직관적이고 최적의 해를 제공하지는 않는 것 같다.

단적으로 내가 작성한 코드는 모든 테스트 케이스에 소요시간이 200ms를 넘지 않는데 순열을 이용한 코드는 3000ms도 소요될때가 있다. 물론 이 문제는 효율성까지 검사하는 문제는 아니다.

지워야하는 순서를 순열을 통해서 정하고,최소횟수를 구하는 방법보다 처음부터 최소횟수를 완전탐색으로 구현하는것이 알고리즘 초보 입장에서 더 구현하기 쉬워보이고 와닿는다.

이 과정에서 (1,1)에 있는 1번 카드와 (2,2)에 있는 1번 카드는 서로 다른 순서로 인식해야 한다.

풀이코드

from collections import deque

dy = [-1, 1, 0, 0]
dx = [0, 0, -1, 1]


def solution(board, r, c):
    def isEnd(s) -> bool:
        for c in s:
            if c != '0':
                return False
        return True

    def OOB(y, x) -> bool:
        if (not 0 <= y < 4) or (not 0 <= x < 4):
            return True
        return False

    def isOnEdgeByDirection(y, x, d) -> bool:

        if d == 0:
            if y == 0:
                return True
        elif d == 1:
            if y == 3:
                return True
        elif d == 2:
            if x == 0:
                return True
        elif d == 3:
            if x == 3:
                return True
        return False

    # 바뀌는 상황 :
    # 카드판의 상황,현재 커서의 위치 , 현재 뒤집었는지? 아니면 안뒤집엇는지 ( 2장째 기다리는중인지 뒤집었다면 커서 위치)

    # 구하는 것 : 최소 회수 이동

    def serialize(board) -> str:
        ret = ''
        for r in board:
            for num in r:
                ret += str(num)

        return ret

    def switchTo0(s:str,num:str) -> int:

        return s.replace(num,'0')

    def idxConverter(y, x) -> int:
        return 4 * y + x

    visit = set()

    # 보드의 상태 ,커서의 위치 , 커서가 카드를 뒤집었는지 , 뒤집힌 카드가 있다면 그 위치
    visit.add((serialize(board), (r, c), False, (-1, -1)))
    q = deque()
    q.append((serialize(board), r, c, False, -1, -1, 0))

    while q:
        b, y, x, isFlipped, f_y, f_x, count = q.popleft()

        # 모든 카드를 뒤집었는지
        # 여기서 체크하면 시간 더걸림
        # if isEnd(b):
        #     return count

        for k in range(4):
            ny, nx = y + dy[k], x + dx[k]

            if OOB(ny, nx):
                continue

            while b[idxConverter(ny, nx)] == '0' and not isOnEdgeByDirection(ny, nx, k):
                ny, nx = ny + dy[k], nx + dx[k]

            if (b, (ny, nx), isFlipped, (f_y, f_x)) in visit:
                continue

            visit.add((b, (ny, nx), isFlipped, (f_y, f_x)))
            q.append((b, ny, nx, isFlipped, f_y, f_x, count + 1))

        # 상하좌우 네방향 이동

        for k in range(4):
            ny, nx = y + dy[k], x + dx[k]

            if OOB(ny, nx):
                continue

            if (b, (ny, nx), isFlipped, (f_y, f_x)) in visit:
                continue

            visit.add((b, (ny, nx), isFlipped, (f_y, f_x)))
            q.append((b, ny, nx, isFlipped, f_y, f_x, count + 1))

        # 현재 한장은 뒤집은 상태에서 다른것 뒤집으려 할때
        if isFlipped:
            # 카드 짝 찾는데 성공하면
            # 0으로 뒤집고
            if b[idxConverter(f_y, f_x)] == b[idxConverter(y, x)] and (f_y, f_x) != (y, x):

                b = switchTo0(b,b[idxConverter(f_y, f_x)])
        

                # 여기서 끝낼수있음

                if isEnd(b):
                    return count + 1

                # print(b)
                visit.add((b, (y, x), False, (-1, -1)))
                q.append((b, y, x, False, -1, -1, count + 1))
                
            # 짝은 안맞으면
            else:

                if (b, (y, x), False, (-1, -1)) in visit:
                    continue
                visit.add((b, (y, x), False, (-1, -1)))
                q.append((b, y, x, False, -1, -1, count + 1))
        # 아직 뒤집지 않은 상태
        # 이제 뒤집기
        else:
            if (b, (y, x), True, (y, x)) in visit:
                continue

            visit.add((b, (y, x), True, (y, x)))
            q.append((b, y, x, True, y, x, count + 1))

백준 난이도로 환산하면 골드2 정도로 보인다.

은근히 테케에 빈틈이 많은 문제다.

첫 시도는 80점 내외로 맞고 조금씩 변경해 80->96->100점을 받을 수 있었다.