수학에서 에라토스테네스의 체는 소수를 찾는 방법이다.
고대 그리스 수학자 에라토스테네스가 발견했다고 한다.
알고리즘
- 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. 그림에서 회색 사각형으로 두른 수들이 여기에 해당한다.
- 2는 소수이므로 오른쪽에 2를 쓴다. (빨간색)
- 자기 자신을 제외한 2의 배수를 모두 지운다.
- 남아있는 수 가운데 3은 소수이므로 오른쪽에 3을 쓴다. (초록색)
- 자기 자신을 제외한 3의 배수를 모두 지운다.
- 남아있는 수 가운데 5는 소수이므로 오른쪽에 5를 쓴다. (파란색)
- 자기 자신을 제외한 5의 배수를 모두 지운다.
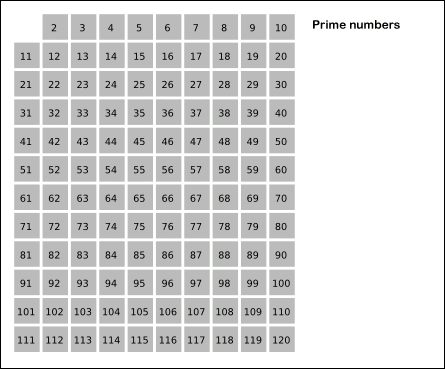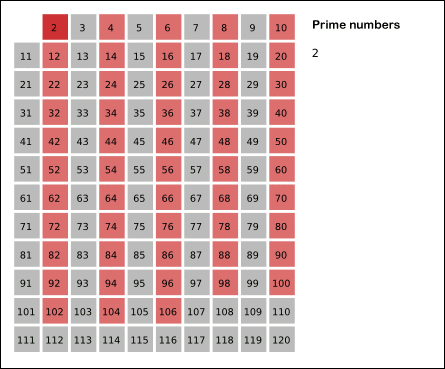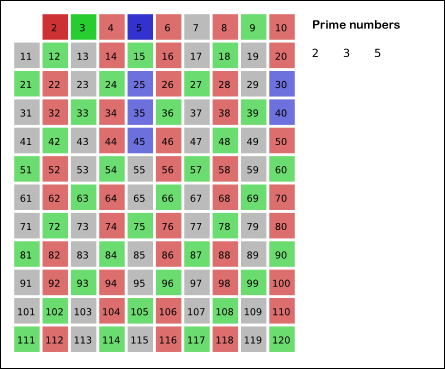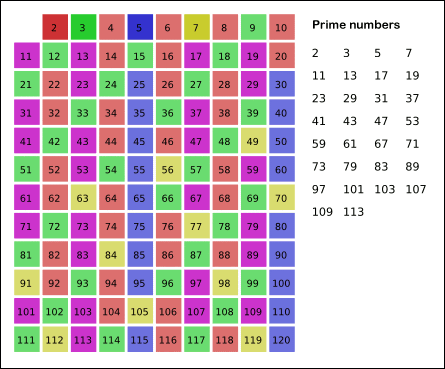
- 남아있는 수 가운데 7은 소수이므로 오른쪽에 7을 쓴다. (노란색)
- 자기 자신을 제외한 7의 배수를 모두 지운다.
- 위의 과정을 반복하면 구하는 구간의 모든 소수가 남는다.
- 그림의 경우 이므로 11보다 작은 배수들만 지워도 충분하다.
파이썬으로 구현한 코드
출처
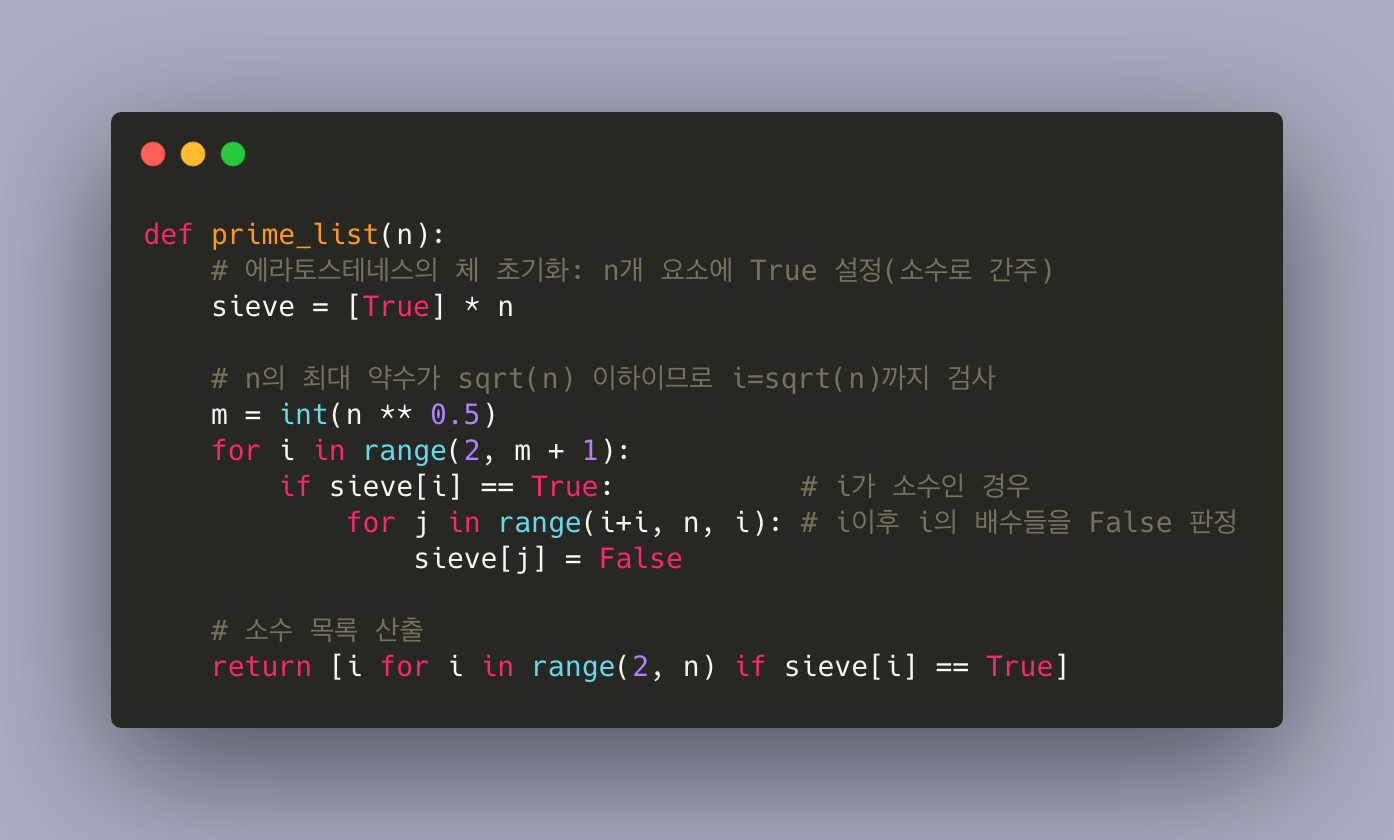
코드에 수정이 필요한 것처럼 보여 작성합니다.
i 이후 i의 배수를 찾는 과정에서 range(2i, n, i)의 코드가 올바르다고 보이는데, 확인 부탁드립니다! :)