📈수학개념📈
📐도함수 📐

도함수 = 기울기
이렇게 생각하는게 편한거 같음
기울기는 함수가 위치하고 있는 지점에 따라 값이 달라질 수 있다
예시 -> f(a)=a2 or f(a)=ln(a)
f(a)=3a 와 같은 그래프는 직선 그래프이기 때문에 기울기가 항상 같다
위 그래프 기준으로 항상 3:1의 비율을 가진다
도함수 공식
dxd[f(x)]
😵보다 복잡한 예제😵
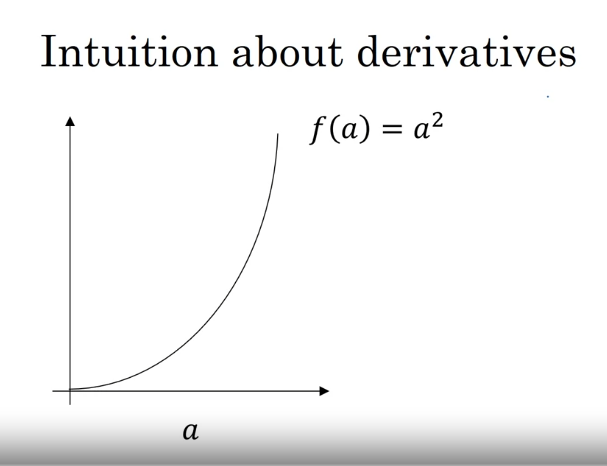
dxdf(x)=dxda2=2a
교과서에 있는 공식이라한다
초등함수의 미분 공식을 보면 알 수 있다!
초등함수 미분공식
상수 함수: f(x)=C의 미분은 f′(x)=0
1차 함수: f(x)=mx+b의 미분은 f′(x)=m
2차 함수: f(x)=ax2+bx+c의 미분은 f′(x)=2ax+b
거듭제곱 함수: f(x)=xn의 미분은 f′(x)=nxn−1 (n은 실수)
지수함수: f(x)=ex의 미분은 f′(x)=ex
로그함수: f(x)=ln(x)의 미분은 f′(x)=x1
삼각함수:
f(x)=sin(x)의 미분은 f′(x)=cos(x)
f(x)=cos(x)의 미분은 f′(x)=−sin(x)
f(x)=tan(x)의 미분은 f′(x)=cos2(x)1=sec2(x)
f(x)=cot(x)의 미분은 f′(x)=−sin2(x)1=−csc2(x)
f(x)=sec(x)의 미분은 f′(x)=cos2(x)sin(x)=sec(x)tan(x)
f(x)=csc(x)의 미분은 f′(x)=−sin2(x)cos(x)=−csc(x)cot(x)
📉 계산그래프 📉
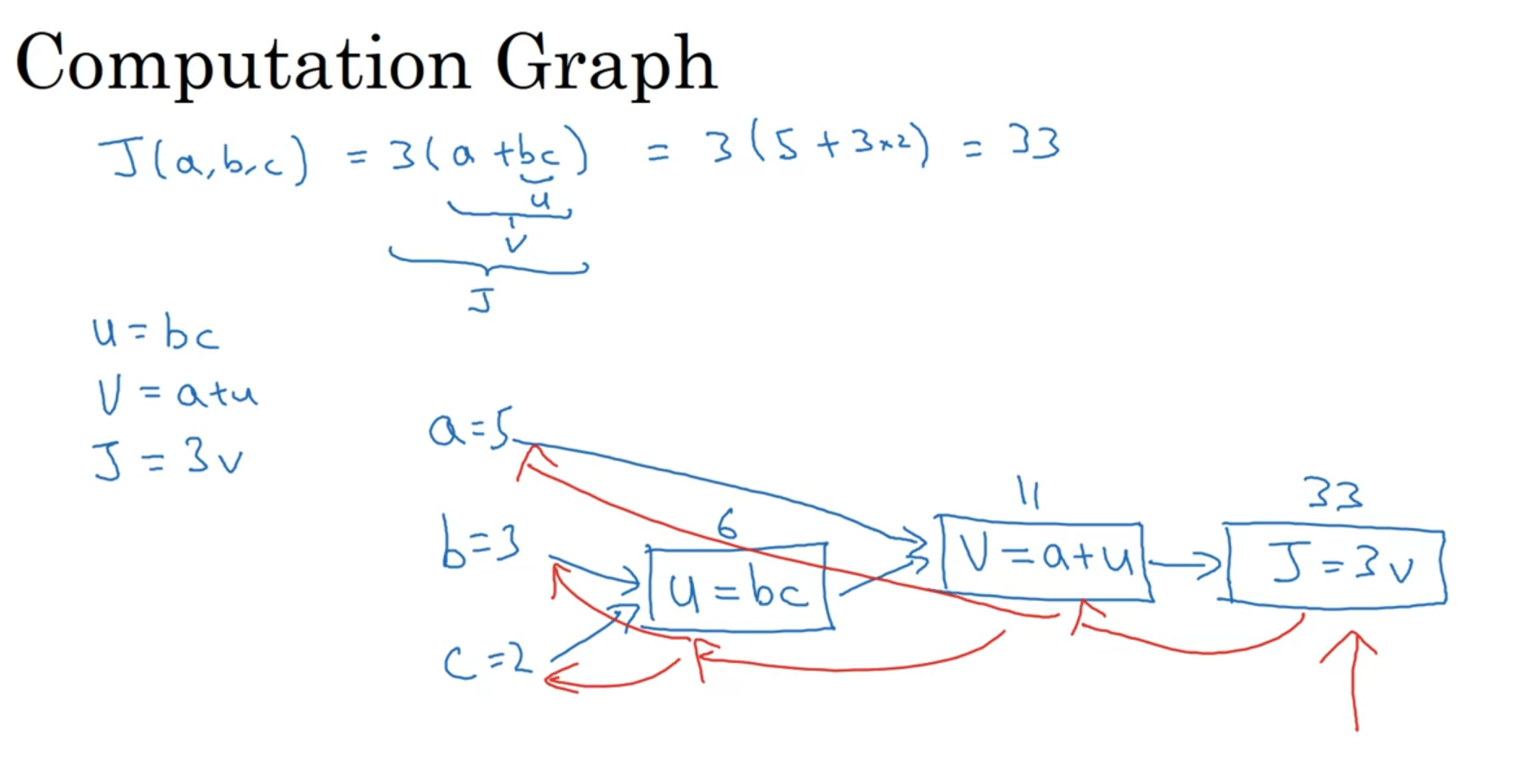
도함수를 계산하기 위해서는 빨간색 선을 따라 계산된다.
깔끔한 버전
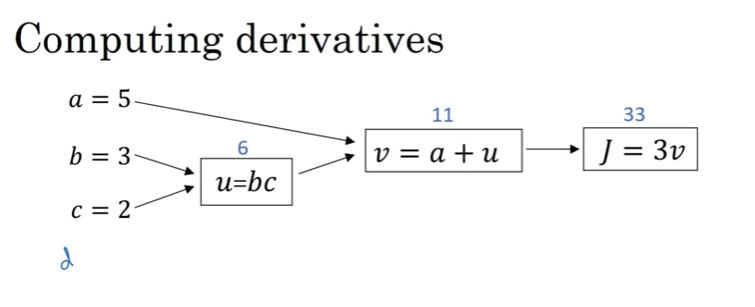
연쇄법칙관련 설명
f(g(x))′=w′(u(x))⋅u′(x)
dxdw=dudw⋅dxdu=w′(u(x))⋅u′(x)
dxdu= u의 x에 대한 도함수
dudw= w의 u에 대한 도함수
함수 f(x)=(3x+1)2의x=2에서의 미분계수
곱의 미분공식
w'(x) = u'(x)v(x) + u(x)v'(x)
- 미분 과정
- 함수 f(x) 정의
먼저, 주어진 함수 f(x)=(3x+1)2를 정의합니다.
f(x)=(3x+1)(3x+1)
- 곱의 미분 공식 적용
f(x)는 두 함수 3x + 1의 곱으로 이루어져 있으므로 곱의 미분 공식 을 적용합니다.
f′(x)=(3)(3x+1)+(3x+1)(3)
- 2.3.3 미분 계산
위 식을 계산하면 다음과 같습니다.
f′(x)=9x+3+9x+3=18x+6
- x=2 대입
x=2에서의 f′(x)를 구하기 위해 x=2를 위 식에 대입합니다.
f′(2)=18(2)+6=36+6=42
연쇄법칙 & 도함수 개념 좀 더 보강하자




