🌱 Heep-Sort ( 힙 정렬 )

👉🏻 힙 정렬 (Heap Sort) : 힙(Heap) 데이터 구조를 기반으로 최대·최소 힙 트리를 구성해 정렬하는 비교 기반 정렬 기술입니다.

• 힙(Heap)은 완전 이진 트리를 기반으로 하는 특별한 데이터 구조입니다. 힙 정렬(Heap Sort)는 그러한 힙(Heap) 데이터 구조를 이용해 정렬하는 알고리즘 기술입니다. 따라서 🚫 힙 정렬에 대해 공부하기 전에 힙 데이터 구조에 대해 선수학습을 한 후에 보는 것을 권합니다.❗️

• 힙 정렬은 컴퓨터의 주 메모리에서 작동하며 데이터를 메모리 상에서 처리하는 내부 알고리즘에 속합니다. 이를 위해 추가 메모리를 사용하지 않거나 상수 크기의 추가 메모리를 사용할 수 있는 In-Place 정렬 알고리즘입니다.
• 일반적으로 불안정 알고리즘입니다. 힙을 구성해 정렬하는 동안 위치가 바뀔 수 있습니다. 👉🏻 동일한 키를 가진 객체에서 위치를 고려하도록 추가 메모리 공간을 사용해 안정적으로 만들 수 있습니다.
• 일반적으로 퀵 정렬보다 2~3배 정도 더 느립니다.

☀️ Characteristic of Heap Sort ( 특징 )

🪴 장 점

• 모든 경우에 O(n log n)의 시간복잡도를 가지므로 대규모 데이터 정렬에 효율적입니다.
• 정렬할 초기 리스트를 보관하는 외에 추가 메모리 공간을 사용하지 않아, 메모리 사용량이 적습니다.
• 재귀를 사용하지 않아 구현이 단순하고 이해하기 쉽습니다.

🪴 단 점

• 초기에 힙 자료구조로 변환하는 데 비용이 많이 듭니다.
• 불안정한 정렬 알고리즘입니다. 따라서 정렬된 데이터의 상대적인 순서가 중요한 경우에는 다른 알고리즘을 선택하는 것이 좋습니다.
• 시간복잡도의 상수 요인은 성능을 측정하는 데 중요합니다. 힙 정렬의 상수 요인은 다른 알고리즘들보다 더 큰 값일 수 있습니다. 작은 규모의 입력 데이터에서는 다른 정렬 알고리즘들이 빠를 수 있습니다.
• 힙 정렬은 주로 배열을 기반으로 데이터를 정렬합니다. 따라서 데이터가 무작위로 분포하는 경우에는 힙 정렬의 성능이 빠르고 효율적이지만 데이터가 거의 정렬되어 있거나 역순으로 정렬되어 있는 경우에는 힙 정렬의 성능이 다른 알고리즘들에 비해 떨어질 수 있습니다.

🪴 활 용

최악의 경우에도 상한이 O(n log n)의 시간으로 보장되어, 컴퓨터 공학 다방면에서 쓰이는 정렬입니다.

• 운영체제에서 메모리를 동적으로 할당하고 효율적으로 관리하는데 쓰입니다.
• 데이터 베이스 관리 시스템에 쓰입니다.
• GUI 👉🏻 예컨대 음악 플레이어 애플리케이션에서 아티스트, 앨범, 노래 제목 등 다양한 기준에 따라 대규모 음악 라이브러리를 정렬합니다.
• 검색엔진에서 결과를 관련도 순으로 정렬하는 데 쓰입니다.

☀️ Operations of Heap Sort ( 작동 )

1. 완전 이진트리 구성

2. heapify ( = sift-down)

• 최대 힙을 구성합니다. heap은 형제관계의 대소관계가 없는 반정렬 상태를 가지므로, 최소힙으로 정렬하면 제대로 정렬되지 않을 수 있습니다.
• 추가적 메모리 공간을 사용하지 않고, 원본 배열 내에서 정렬하기 위해 힙으로 저장해 반환하지 않고, 구현합니다.

3. root의 가장 큰수와 가장 작은 수를 교환한다.

4. 위 과정을 반복해 최대 힙으로 재구성한다.

• tree의 깊이만큼 n개에 대해 반복하므로 시간복잡도는 O(n log n)이 됩니다.

☀️ Implement of Heap Sort ( 구현 )

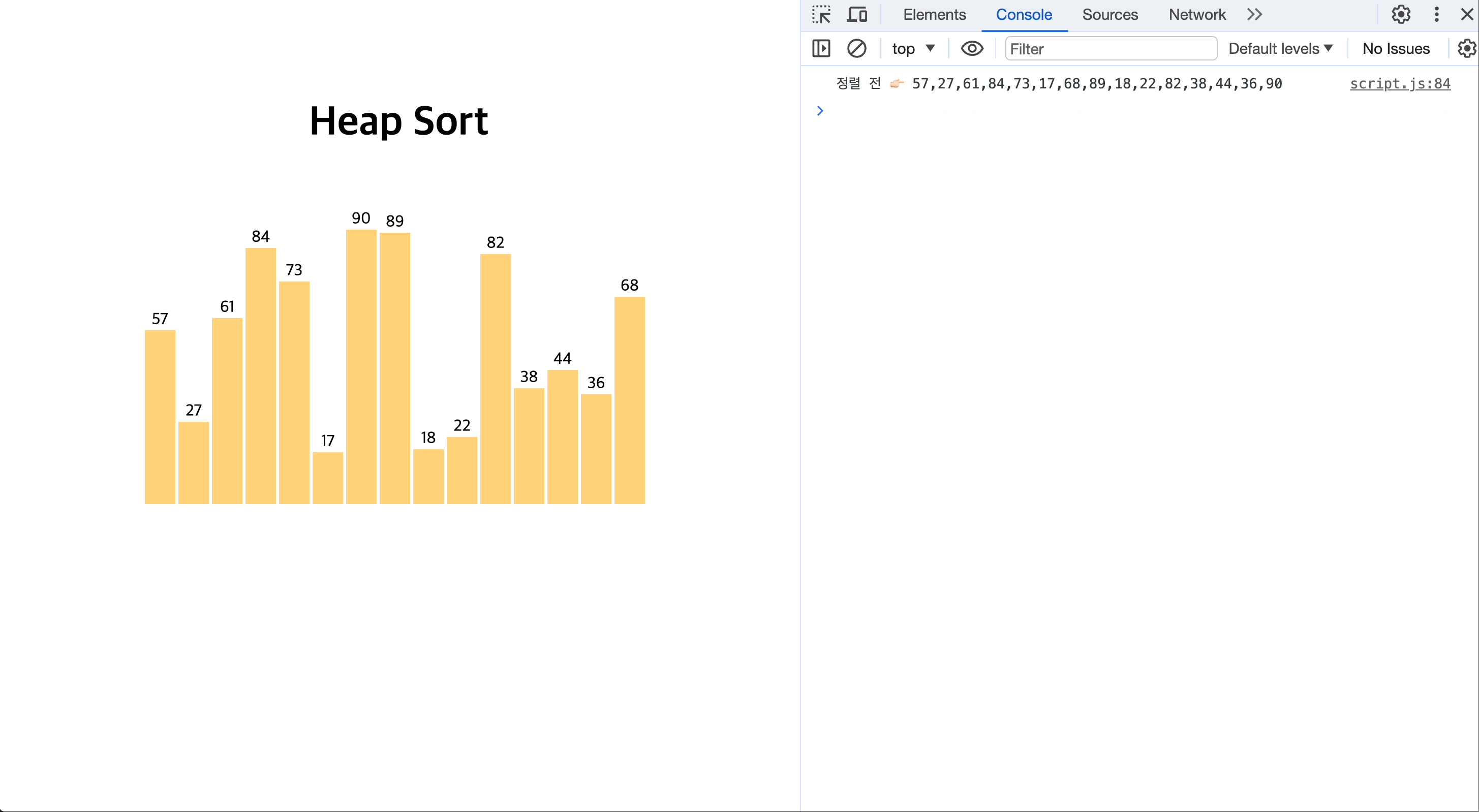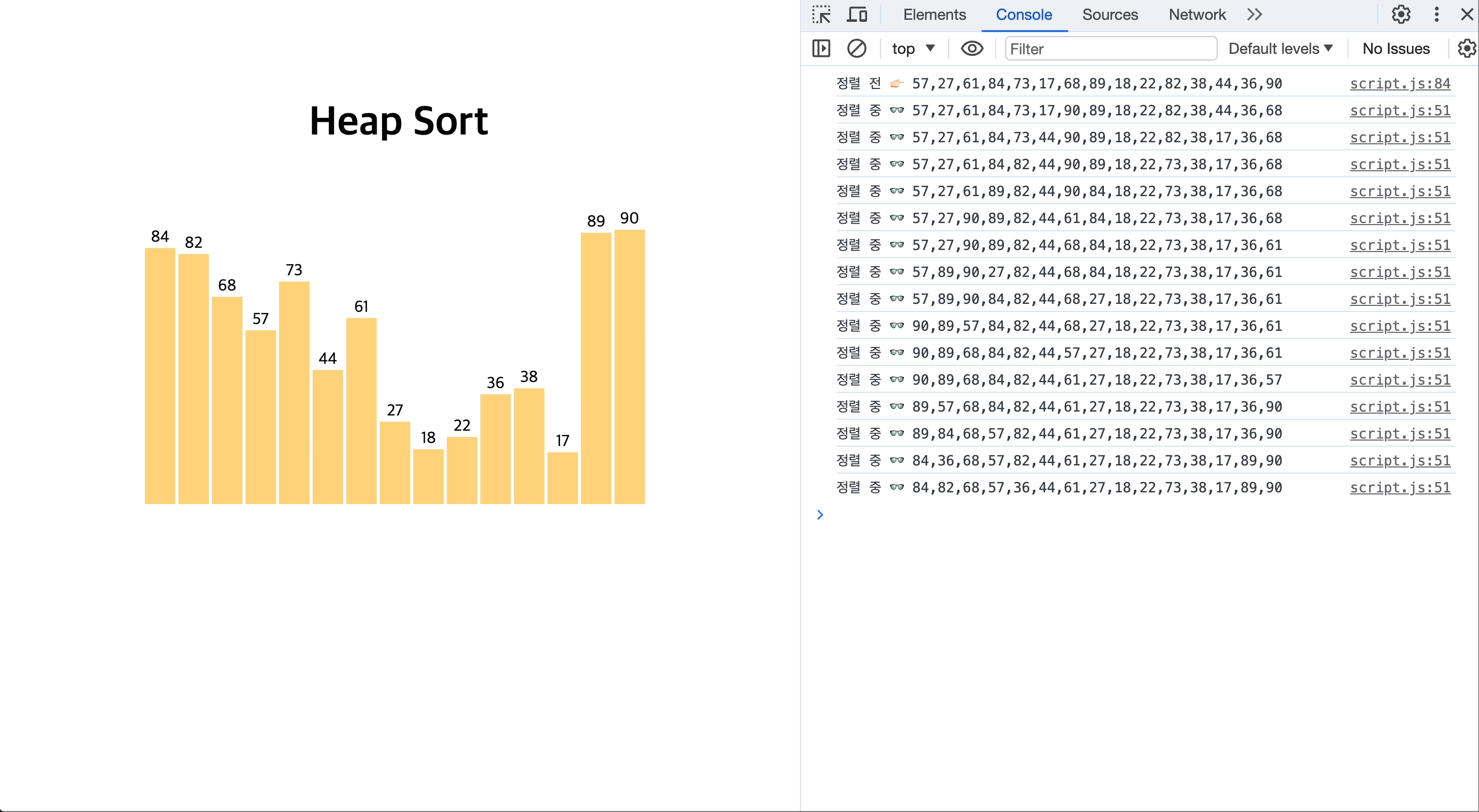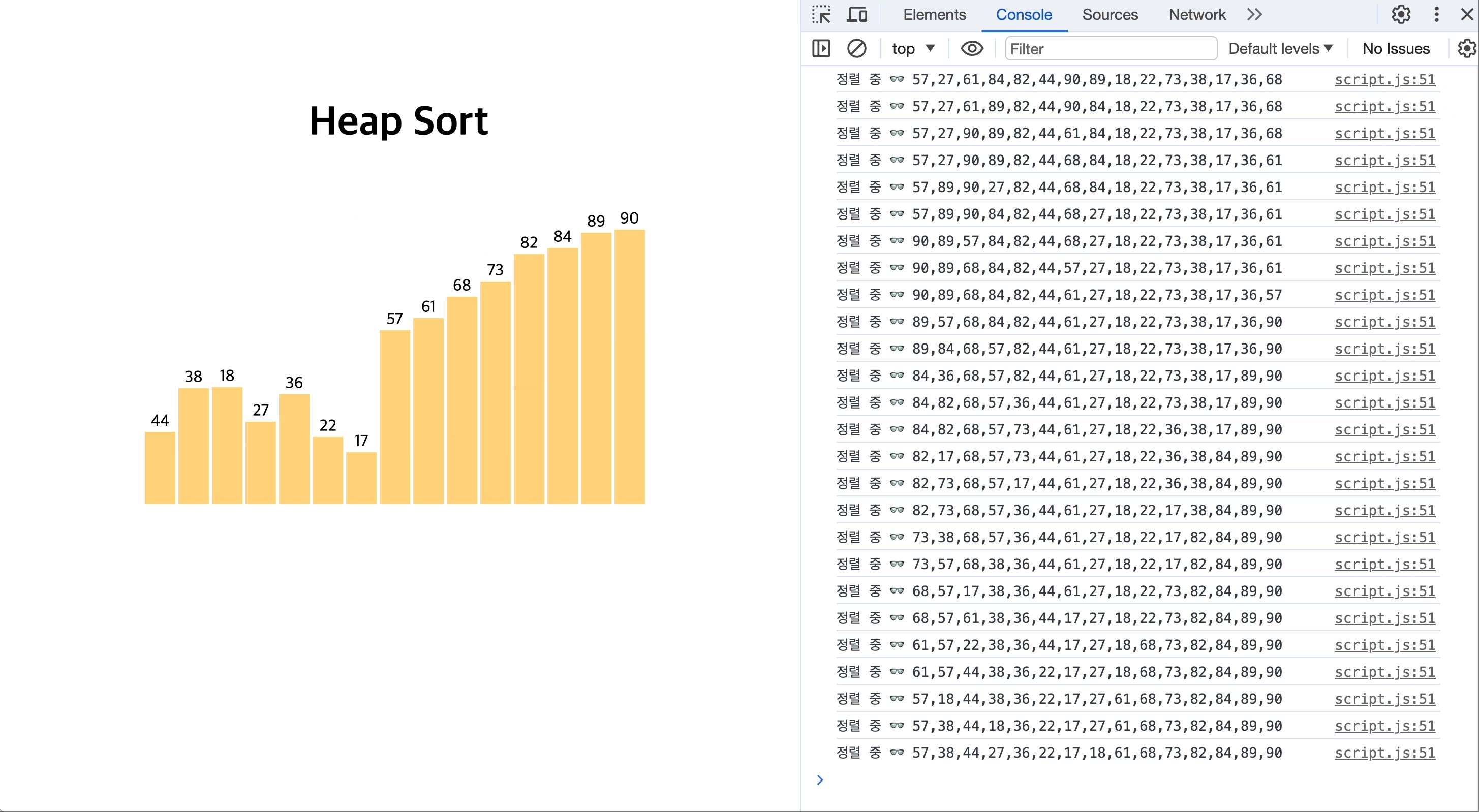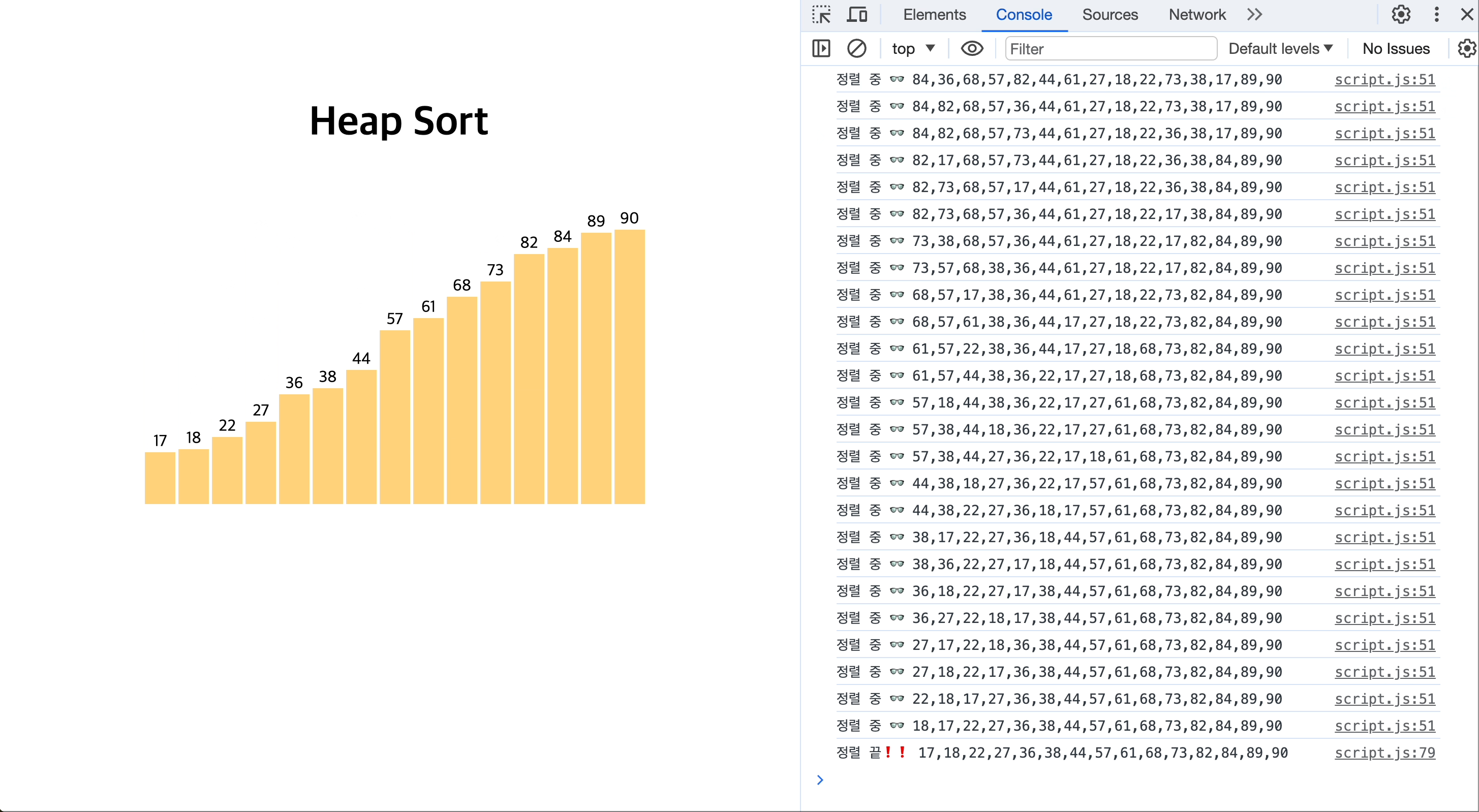
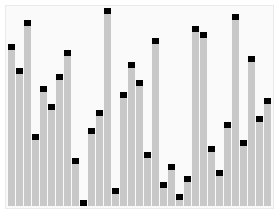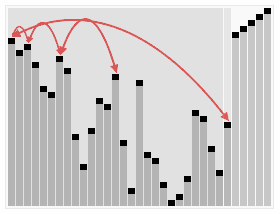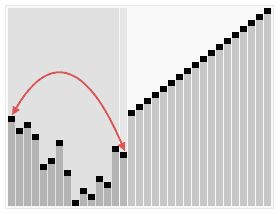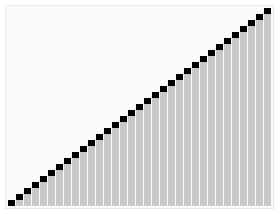
[JavaScript로 힙 정렬하는 모습을 시각화 👉🏻 GitHub repository]

🪴 Max-heap

function heapify(arr, lastIdx, parentIdx) {
  // 부모 idx를 가장 큰 값이라고 가정합니다.
  let maxIdx = parentIdx;
  // 현재 트리에서 자식 노드의 idx를 구합니다.
  let left = 2 * parentIdx + 1;
  let right = 2 * parentIdx + 2;
  
  // 자식 노드의 인덱스가 끝 인덱스를 넘지 않고, 왼쪽 자식 노드의 값이 부모 노드의 값보다 크다면
  // max에 왼쪽 노드 인덱스를 넣어준다.
  if(left < lastIdx && arr[left] > arr[maxIdx]) maxIdx = left;
  // 오른쪽 자식 노드에도 동일하게 조건을 검사한다.
  if(right < lastIdx && arr[right] > arr[maxIdx]) maxIdx = right;
  
  // maxIdx의 값이 바뀌었다면
  if(maxIdx !== parentIdx) {
    // 노드의 위치를 바꾸어 줍니다.
    [arr[parentIdx], arr[maxIdx]] = [arr[maxIdx], arr[parentIdx]];
    // 재귀호출을 이용해 바뀐 자식노드의 idx를 부모노드의 파라미터해, 부모노드로 삼은 서브트리를 다시 검사합니다.
    heapify(arr, lastIdx, maxIdx); 
  }
}

function buildHeap(arr) {
  let len = arr.length;
  // 가장 마지막 노드의 부모 노드 서브트리부터 root 노드까지 검사합니다.
  // ❗️ 자식 노드가 없는 부모노드는 검사할 게 없으므로 가장 마지막 노드부터 검사하는 것이 아닙니다!
  for(let i = Math.floor(len / 2) -1; i >= 0; i--) {
    heapify(arr, len, i);
  }
}

🪴 Min-heap

우선 최대힙을 구성한 다음, root의 최댓값을 맨 마지막 노드로 보내고 그 노드를 제외한 나머지를 다시 최대힙을 정렬하는 과정을 반복하면서 맨 뒤부터 큰 수로 채워서 정렬합니다.

function heapify(arr, lastIdx, parentIdx) {
  let minIdx = parentIdx;
  let left = 2 * parentIdx + 1;
  let right = 2 * parentIdx + 2;

  if(left < lastIdx && arr[left] < arr[minIdx]) minIdx = left;
  if(right < lastIdx && arr[right] < arr[minIdx]) minIdx = right;
  
  if(minIdx !== parentIdx) {
    [arr[parentIdx], arr[minIdx]] = [arr[minIdx], arr[parentIdx]];
    heapify(arr, lastIdx, minIdx); 
  }
}

function buildHeap(arr) {
  let len = arr.length;
  for(let i = Math.floor(len / 2) -1; i >= 0; i--) {
    heapify(arr, len, i);
  }
  // 최댓값을 마지막으로 보내고 다시 정렬하는 과정을 거칩니다.
  for(let i = n - 1; i >= 0; i--) {
    [arr[0], arr[i]] = [arr[i], arr[0]];
    heapify(arr, i, 0);
}

🪴 반복문으로 최적화

heapify를 진행하는 과정에서 재귀적으로 계속 호출을 하므로 배열이 크다면 stackoverflow의 위험이 있습니다. 이를 개선하기 위해 재귀 호출 대신 반복문으로 구현할 수 있습니다.

function heapify(arr, lastIdx, parentIdx) {
  let maxIdx;
  let left;
  let right;
  
  // 현재 부모 인덱스의 자식 노드 인덱스가 마지막 인덱스를 넘지 않을 때까지 반복한다.
  // 마지막 부모 인덱스가 왼쪽 자식 노드만 가지고 있을 경우를 고려해,
  // 왼쪽 자식 노드를 기준으로 한다.
  while(parentIdx * 2 + 1 <= lastIdx) {
    left = 2 * parentIdx + 1;
    right = 2 * parentIdx + 2; 
    maxIdx = parentIdx;
    
    // 왼쪽 자식 노드 비교에서 left <= lastIdx 부분은 while문 조건에서 하고 있으므로 제외해준다.
    if(arr[left] > arr[maxIdx]) maxIdx = left;
    if(right <= lastIdx && arr[right] > arr[maxIdx]) maxIdx = right;
    
    if(maxIdx !== parentIdx) {
      [arr[parentIdx], arr[maxIdx]] = [arr[maxIdx], arr[parentIdx]];
      // 교환 후에 교환된 자식노드를 부모노드가 되도록 idx를 재할당 해준다.
      parentIdx = maxIdx;
    }
    else return;
}

🌈 Finish

• heap 자료구조 글을 본 지인이 heapify가 없대서 조사를 해본 결과, heap 자료 구조와 heap-sort 알고리즘의 차이에 대해 조금은 알게 되었다. 그러면서 조사한 heap sort에 대해도 정리하게 되었다. (내 지인 칭찬해~🙃)
• 정렬에 대해 공부하면 할 수록 이렇게 한 번 구현코드를 찾고 적어본다고 아는 문제가 아니라는 생각이 든다..🥲 어떻게 하면 정말로 정렬에 대해 알 수 있을 지 많은 고민을 하게 되었다.

👀 Reference

• 자바 [JAVA] - 힙 정렬 (Heap Sort)
• Heap Sort – Data Structures and Algorithms Tutorials