🌱Linked List ( 연결 리스트 )

👉🏻 연결 리스트 (Linked-List) : 각 노드가 데이터(값)와 포인터(다음 노드의 주소, 참조값)를 가지고 한 줄로 연결되어 있는 방식으로 데이터를 저장하는 자료구조입니다. 노드의 포인터가 다음 혹은 이전의 노드와 연결되어 선형 데이터 구조를 가집니다. 다른 선형 데이터 구조에 비해 런타임에 크기를 조절할 수 있고 삽입 및 삭제가 쉽습니다.

• 각 노드는 데이터와 다음 노드의 주소(포인터)를 가져야 하므로, 배열보다 더 많은 메모리를 필요로 합니다. 또 이중 연결 리스트의 경우에는 이전 노드의 주소(포인터)까지 가져야 하므로 더 큰 메모리를 필요로 합니다. 하지만 요구 사항에 따라 크기를 증감할 수 있어 메모리 낭비를 방지할 수 있습니다.

• 동적 데이터 요소를 처리하는 데 가장 일반적으로 사용됩니다. 다른 선형 데이터 구조에 비해 연결 리스트를 사용하면 런타임에 크기를 조절할 수 있고 쉽게 삽입하고 삭제할 수 있고 노드의 중간 지점에서도 삽입과 삭제가 O(1)시간에 가능합니다. 삽입 및 삭제 후 요소를 이동할 필요가 없고 주소만 업데이트하면 되기 때문입니다.

• 그러나 특정 위치의 데이터를 검색하는 데는 다른 자료구조보다 느린 O(n)시간이 걸립니다. 따라서 강력하고 유연한 데이터 구조이지만, 사용 여부를 결정할 때 빠른 액세스 시간이 필요하다면 배열이나 트리와 같은 자료구조가 더 효율적입니다.

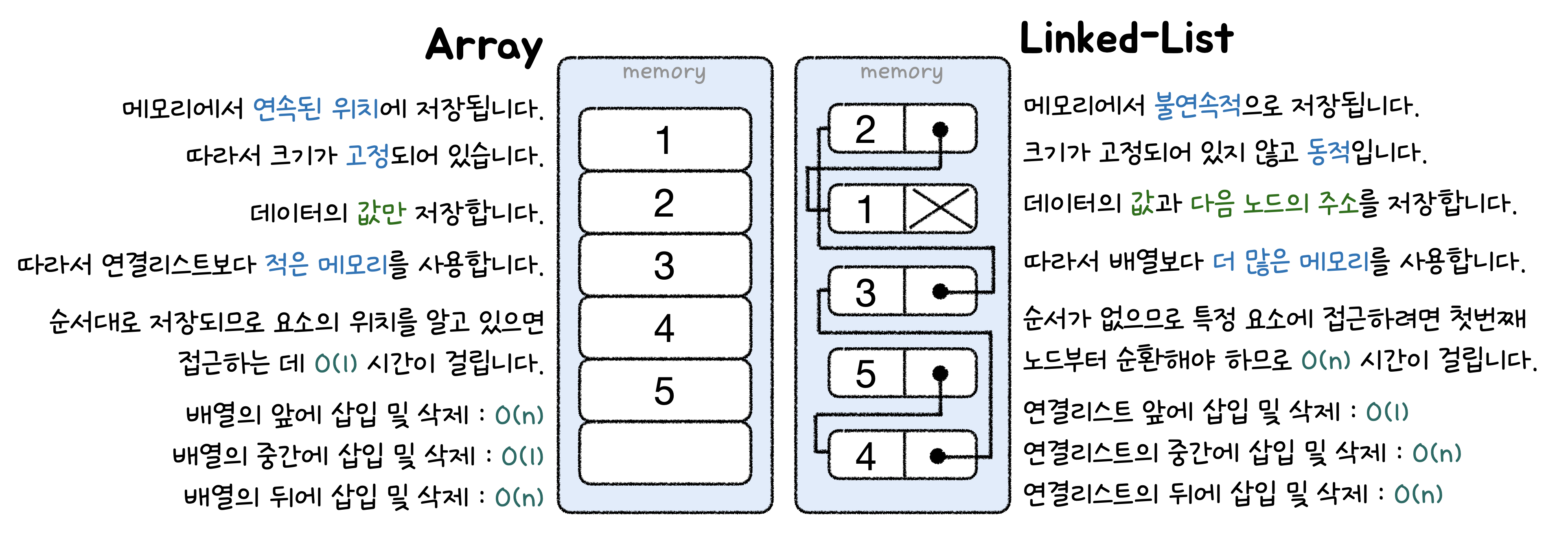
🌿 vs. Array ( 배열과 비교 )

👉🏻 연결 리스트는 주소 저장에 필요한 추가 공간이 들지만, 이를 통해 삽입﹒삭제﹒업데이트와 같은 기본 작업을 수행하는 효율적인 방법을 제공해 배열에 비해 작업이 빠릅니다. 또한 메모리 크기가 동적이어서 삽입﹒삭제에 따라 런타임 시에 메모리크기를 할당하거나 할당을 해제할 수 있어 특정한 경우에 배열보다 선호됩니다.

• Array ( 배열 )	Linked List ( 연결 리스트 )
  연속된 위치에 저장됩니다.	불연속적으로 저장되며 포인터를 통해 서로 연결됩니다.
  크기가 고정되어 있습니다.	동적이고 유연하여 크기를 확장하거나 축소할 수 있습니다.
  메모리는 컴파일 시 할당됩니다.	메모리는 런타임시에 할당됩니다.
  연결리스트보다 적은 메모리를 사용합니다.	데이터와 포인터를 저장하므로 배열보다 많은 메모리를 사용합니다.
  특정 요소에 접근하는데 O(1) 시간이 걸립니다.	특정 요소에 접근하려면 순회해야 하므로 O(n) 시간이 걸립니다.
  삽입, 삭제, 업데이트에 연결리스트보다 많은 시간이 걸립니다.	삽입, 삭제, 업데이트에 배열보다 작업이 빠릅니다.
  배열의 앞에 삽입 및 삭제 : O(n) / 배열의 중간에 삽입 및 삭제 : O(1) / 배열의 뒤에 삽입 및 삭제 : O(n)	연결리스트의 앞에 삽입 및 삭제 : O(1) / 중간에 삽입 및 삭제 : O(n) / 뒤에 삽입 및 삭제: O(n)
  정렬이 되어 있다면 이진 검색을 적용해 O(log n) 시간으로 모든 요소를 검색할 수 있습니다.	정렬이 되어 있더라도 이진 검색을 적용할 수 없어 O(n)의 복잡성이 걸립니다.

☀️ Characteristic of Linked-List ( 특징 )

🪴 장 점

• 연결 리스트는 동적 메모리 할당에 사용됩니다.
• 어느 위치에서든 노드의 삽입 및 삭제가 용이합니다.

🪴 단 점

• 포인터 사용은 연결 리스트에서도 많이 사용되어 복잡하고 더 많은 메모리가 필요합니다. 연결 리스트의 각 노드는 다음 노드에 대한 참조를 저장하기 위해 추가 메모리가 필요하므로 배열에 비해 더 높은 오버헤드를 갖습니다.
• 동적 메모리 할당으로 임의 노드에 접근이 불가능합니다.
• 연결 리스트는 메모리가 인접하지 않기 때문에 캐시가 비효율적입니다. 연결 리스트를 탐색할 때 필요한 데이터를 캐시에서 얻을 가능성이 적고, 이로 인해 캐시가 누락되고 성능이 저하된다는 의미입니다.

🪴 활 용

• 스택, 큐, 해시 맵, 그래프와 같은 데이터 구조의 구현에 사용됩니다. 특히 그래프의 인접 리스트 표현은 연결 리스트를 사용해 인접 정점을 저장하는 방법으로 가장 널리 사용됩니다.
• 웹 브라우저와 편집기에서는 이중 연결 리스트를 사용해 앞으로 및 뒤로 탐색 버튼을 만들 수 있습니다.
• 대규모 데이터 컬렉션에서 항목을 자주 삽입하거나 삭제해야 하는 알고리즘의 성능을 향상시킬 수 있습니다.
• 실생활에서 가장 쉽게 볼 수 있는 예는 휴대폰에 연락처를 저장할 때, 새로운 연락처가 알파벳 순서대로 배치되는 것입니다. 연결 리스트를 통해 알파벳 위치에 맞추어 추가됩니다.

☀️ Type & Implements ( 유형 및 구현 )

🪴 Singly Linked List ( 단일 연결 리스트 )

• 데이터와 다음 노드의 주소를 저장합니다. 모든 노드가 다음 노드에만 연결되어 있으므로 순회는 한 방향으로만 가능합니다. (즉, 역방향 탐색은 불가능하여 탐색시 시간이 더 많이 걸릴 수 있습니다.)

🕶️ 노드 생성

class Node {
    constructor(data, next = null) {
        this.data = data;
        this.next = next;
    }
}

🕶️ 맨 앞에 노드 삽입

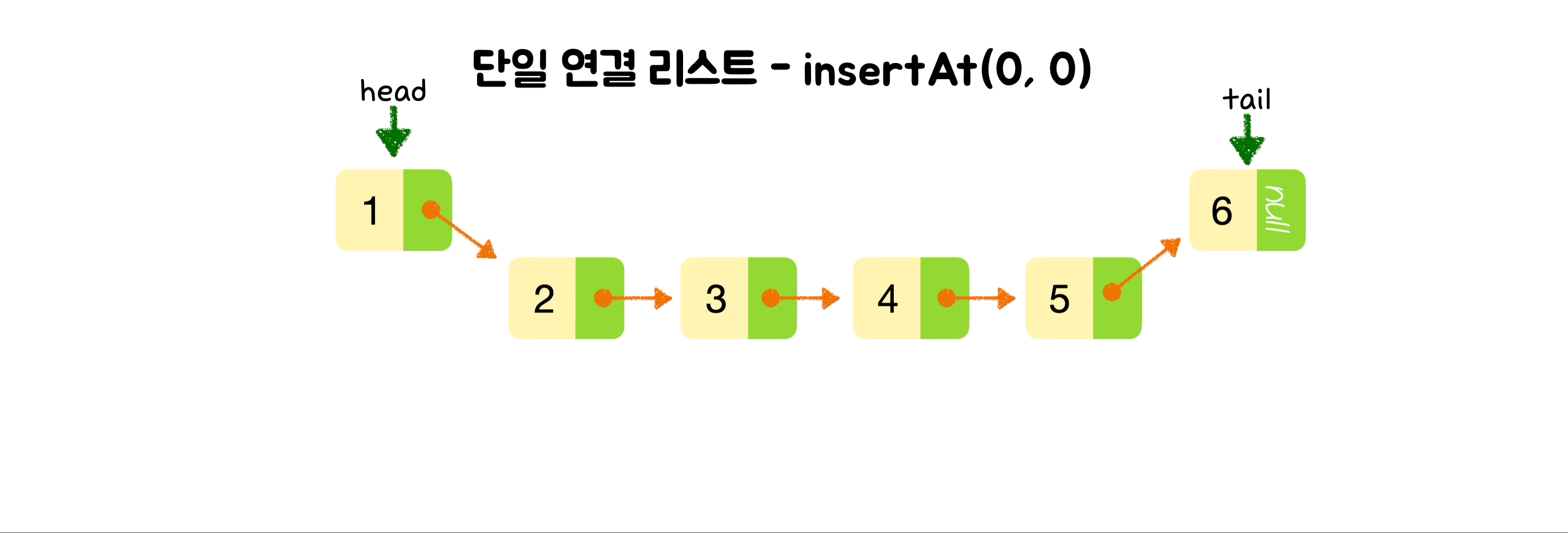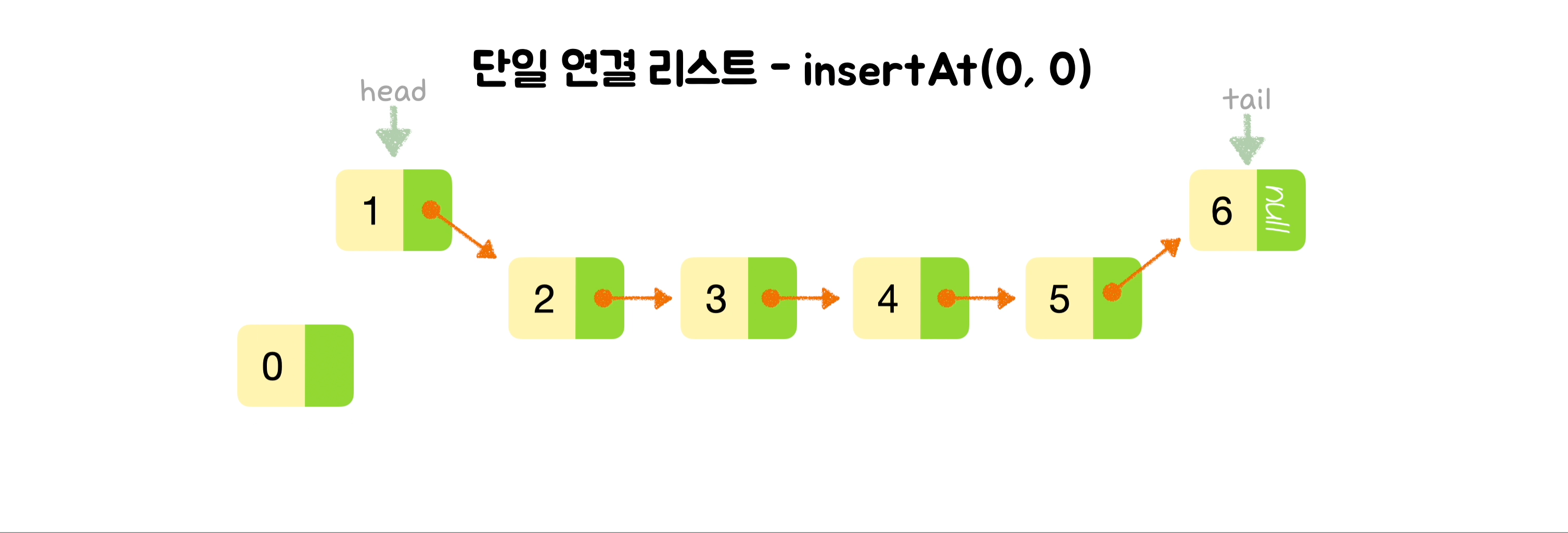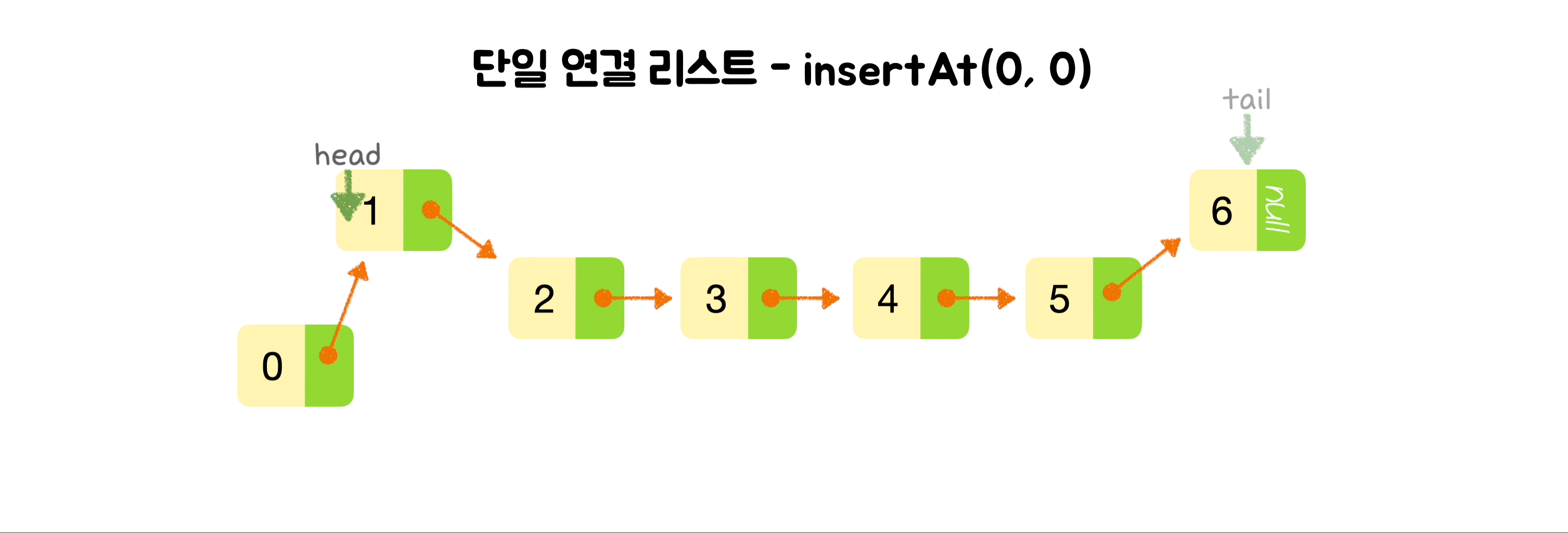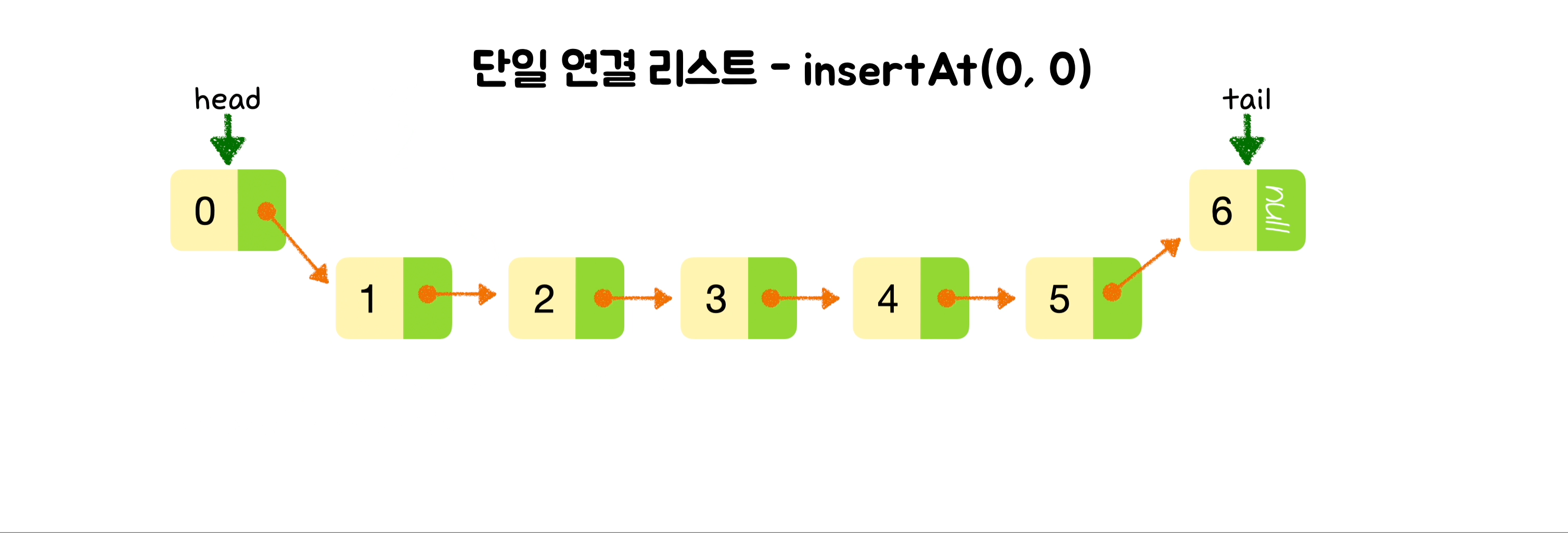
class SinglyLinkedList {
    constructor() {
        this.head = null;
      	this.count = 0;
    }
  
  	// 넣을 위치(index), 넣을 값(value)
    insertAt(index, value) {
      	// 넣을 위치가 음수거나 범위를 벗어난 경우의 예외를 처리합니다.
        if (index > this.count || index < 0) {
            throw new Error('범위를 넘어갔습니다.🤦🏻‍♀️');
        }

        let newNode = new Node(value);
		// 맨 앞인 경우와 그외의 경우로 나누어 구현합니다.
        if (index === 0) {
          	// 맨 앞인 경우 새로만든 노드의 다음 주소로 현재 노드를 추가해주고,
            newNode.next = this.head;
          	// head로 새 노드를 넣습니다.
            this.head = newNode;
        }

🕶️ 특정 위치에 노드 삽입

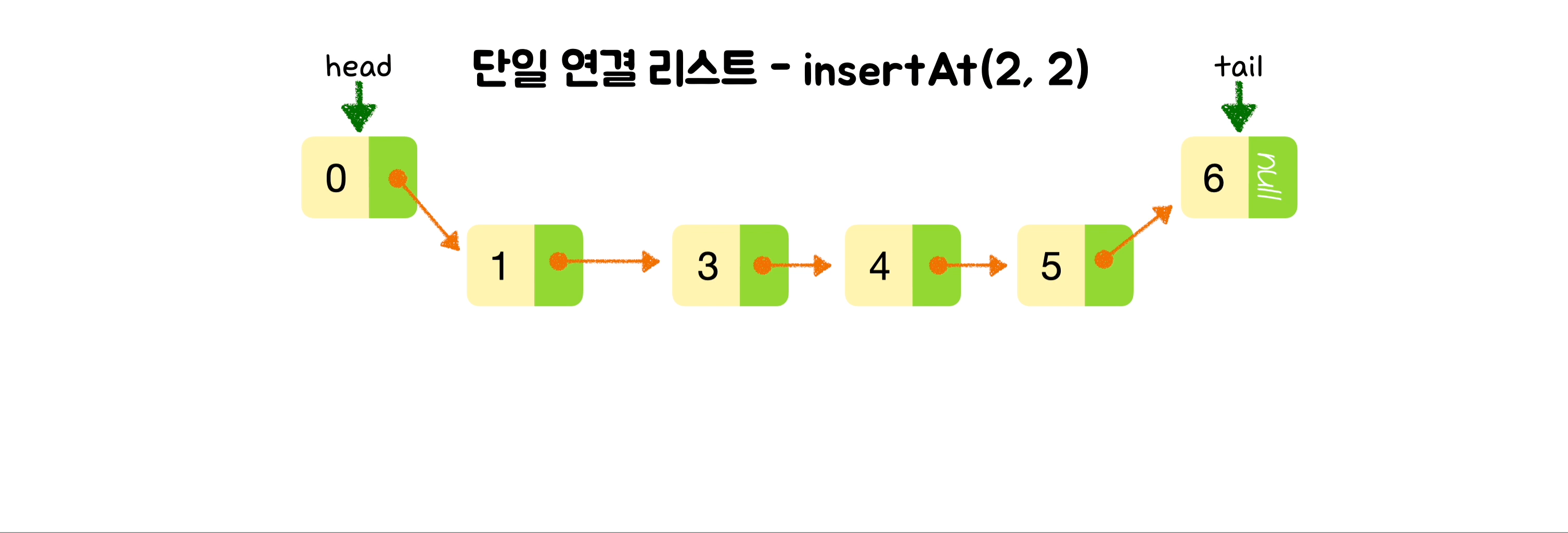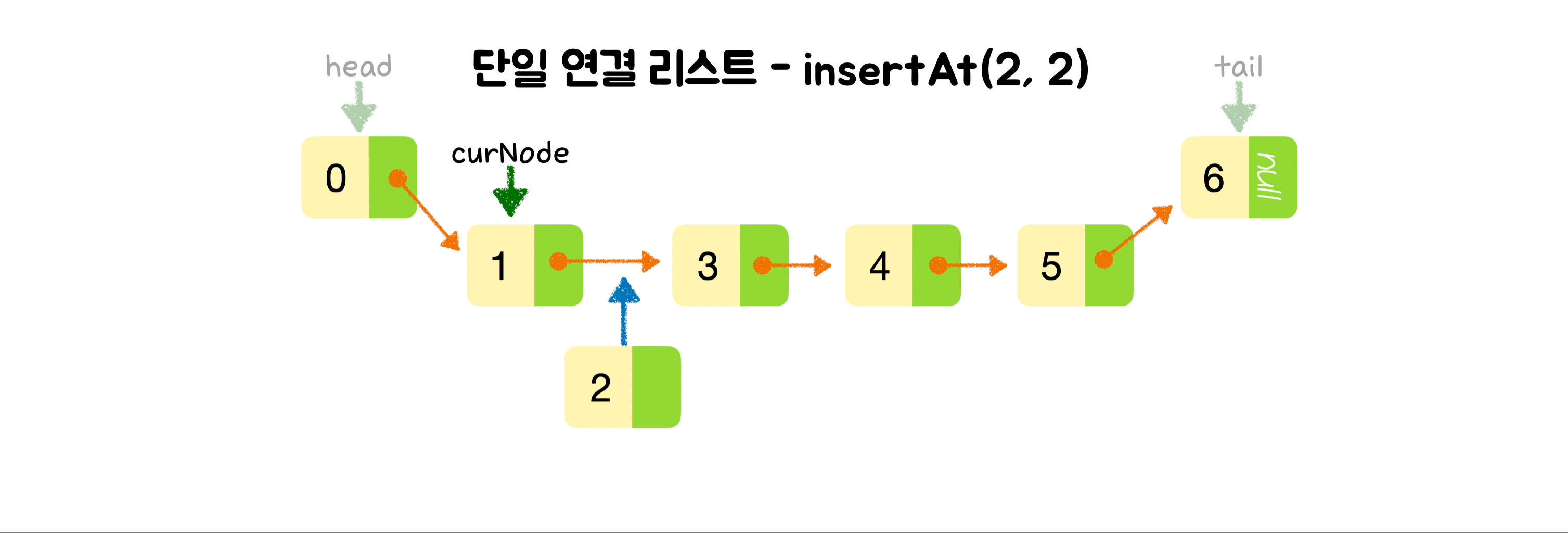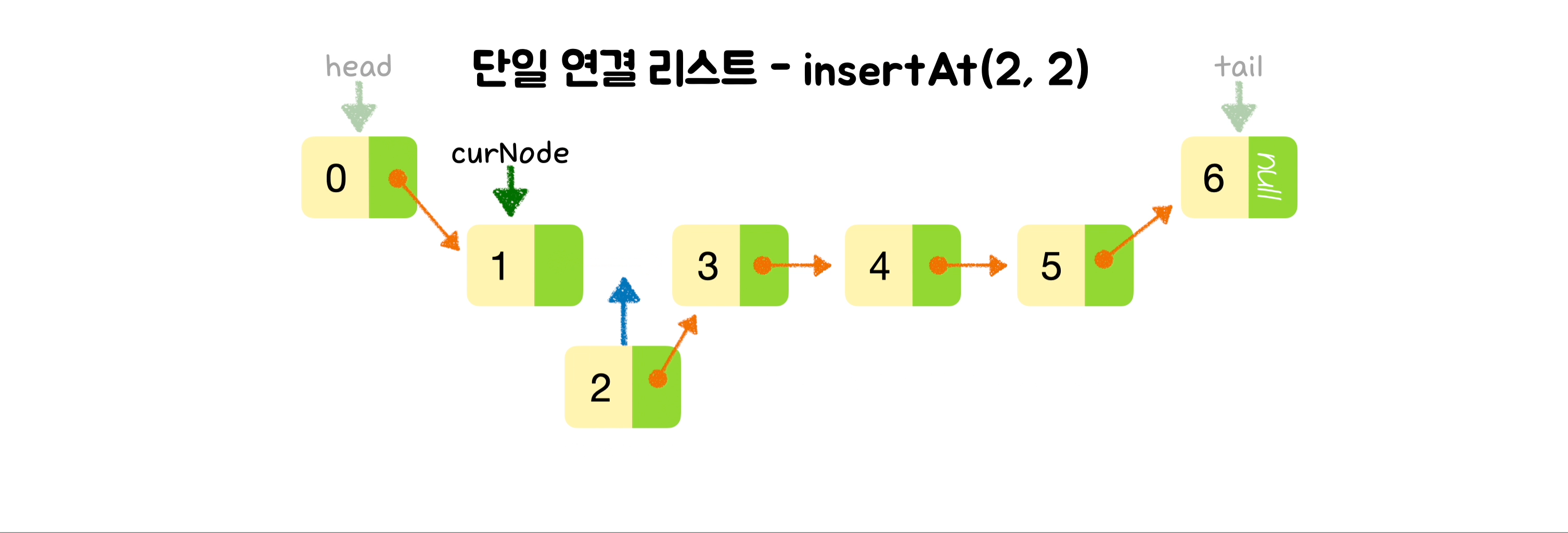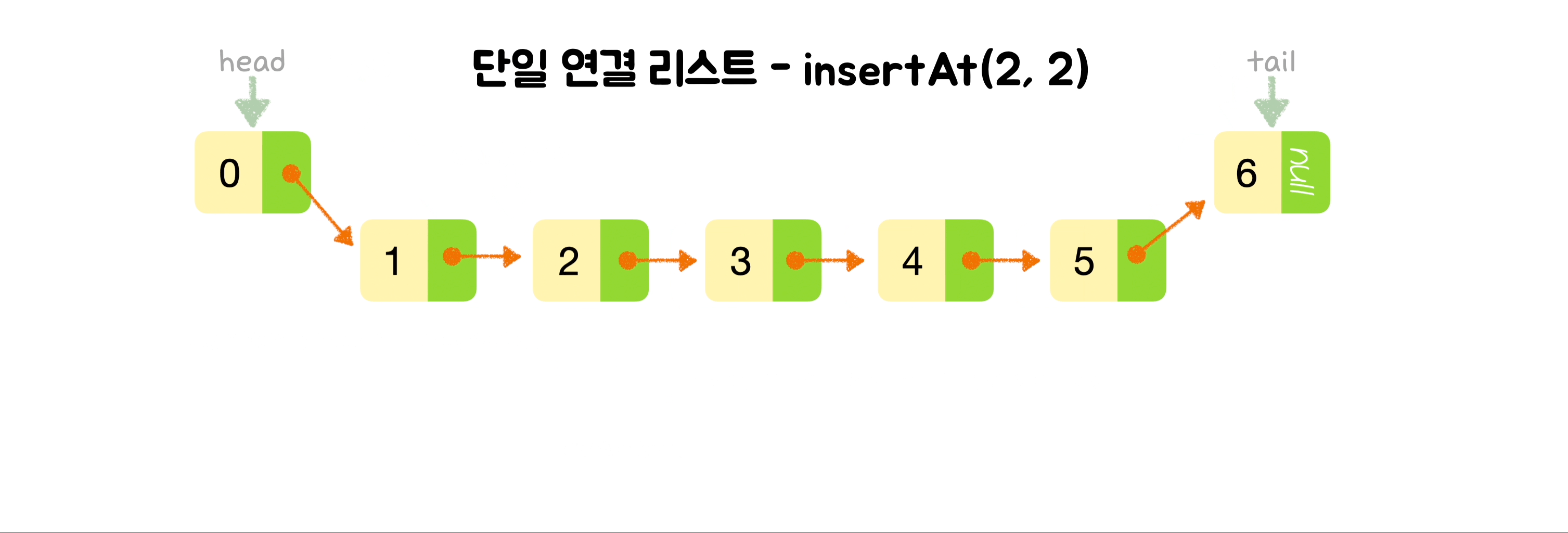
 		else {
          	// 그 외의 경우 현재 위치를 추적하는 포인터를 하나 더 만들고,
            let curNode = this.head;
			// 넣으려는 위치 바로 전 위치까지 이동합니다.
            for (let i = 0; i < index - 1; i++) {
                curNode = curNode.next;
            }
          	// 새 노드의 다음 노드 주소로 현재 노드의 다음 주소를 넣고,
            newNode.next = curNode.next;
          	// 현재 노드의 다음주소로 새로 만든 노드를 넣습니다.
            curNode.next = newNode;
        }
      this.count++;
    }
	
  	// 맨 뒤에 추가
    insertLast(value) {
        this.insertAt(this.count, value);
    }

🕶️ 맨 앞 노드 삭제

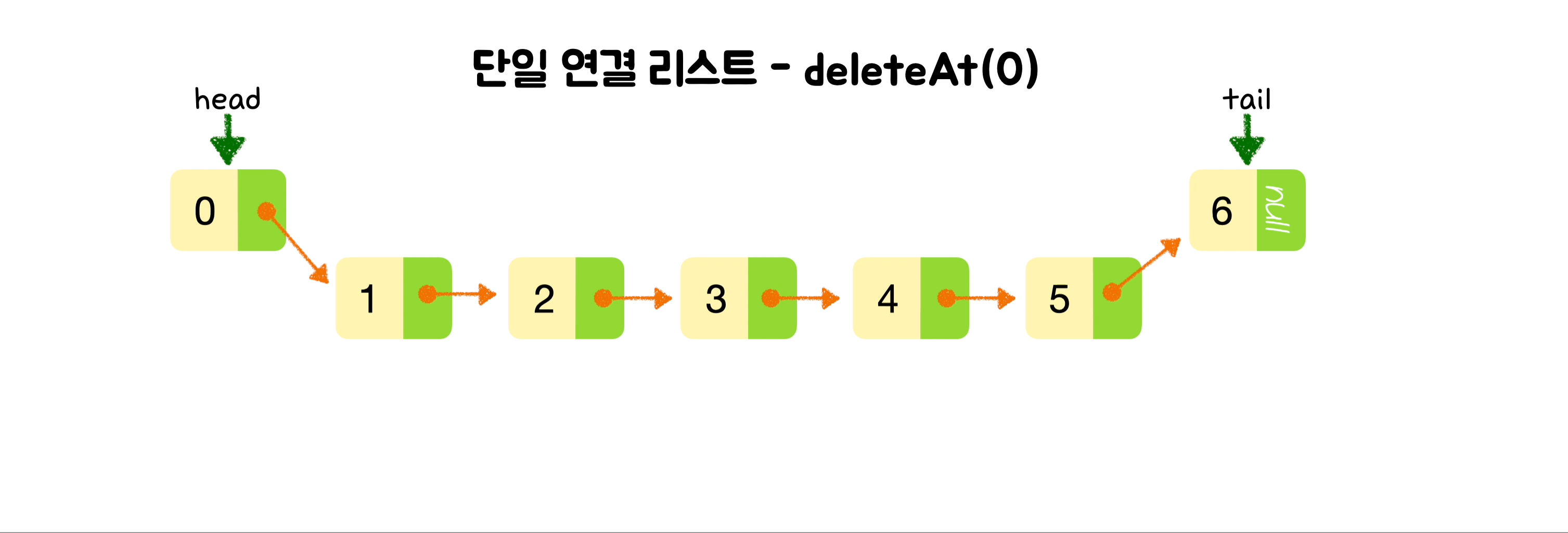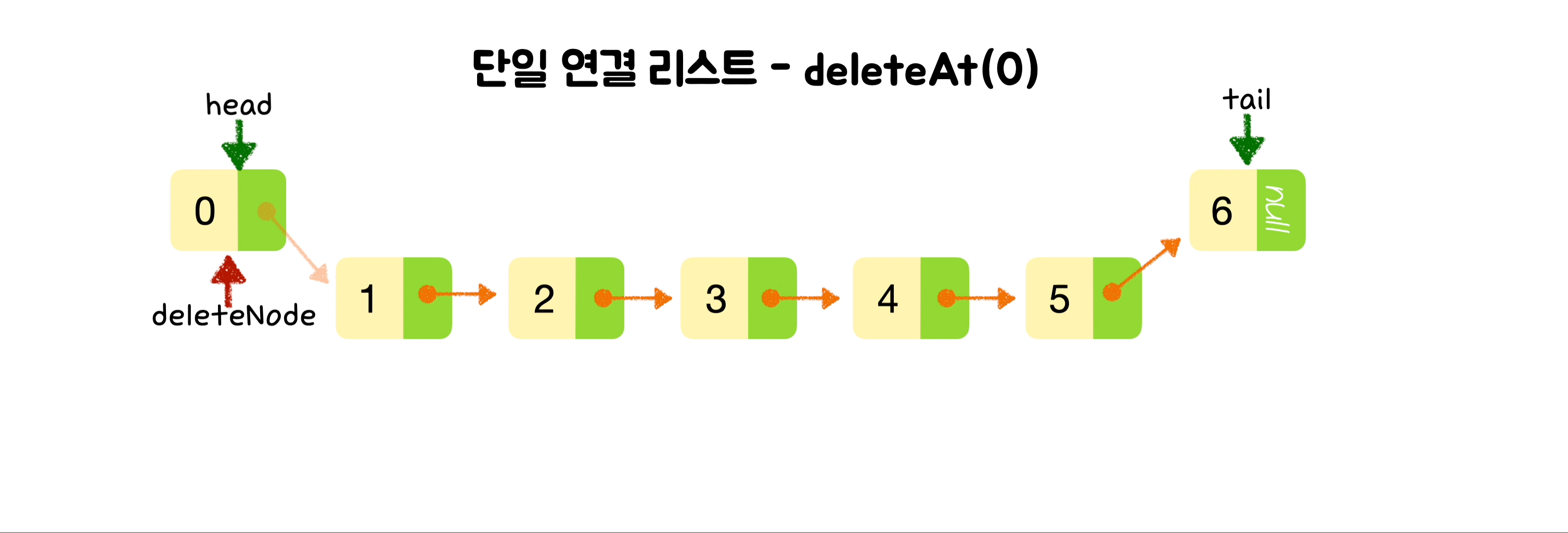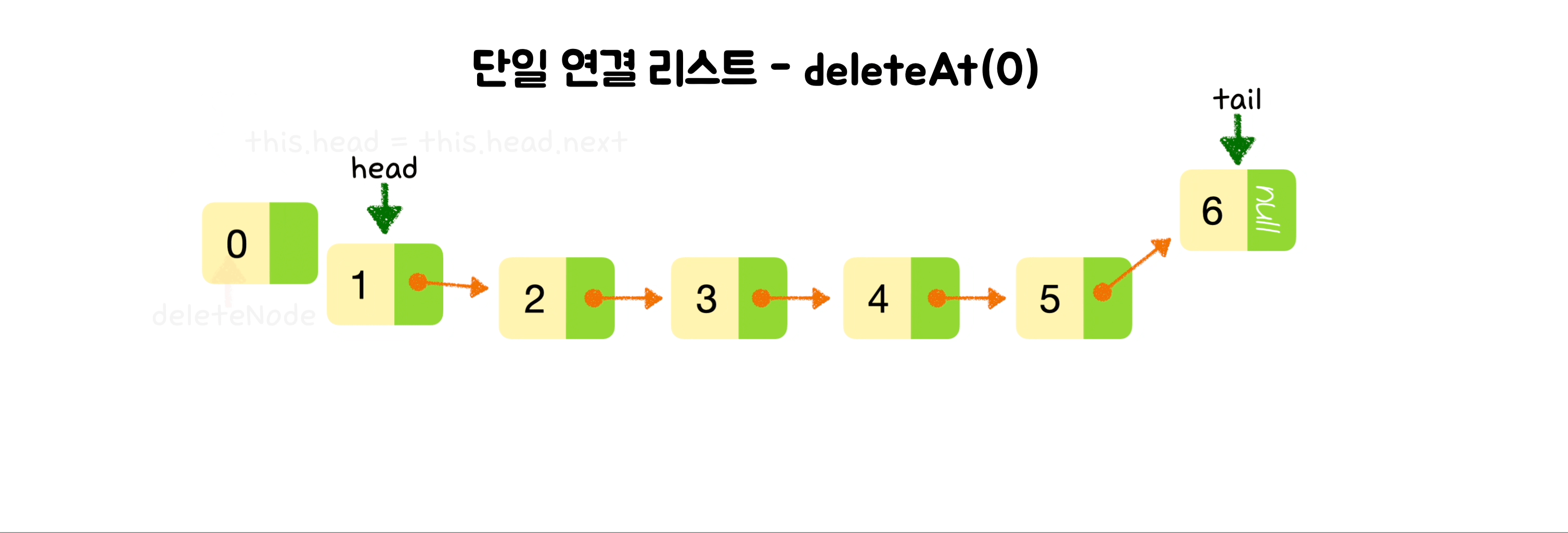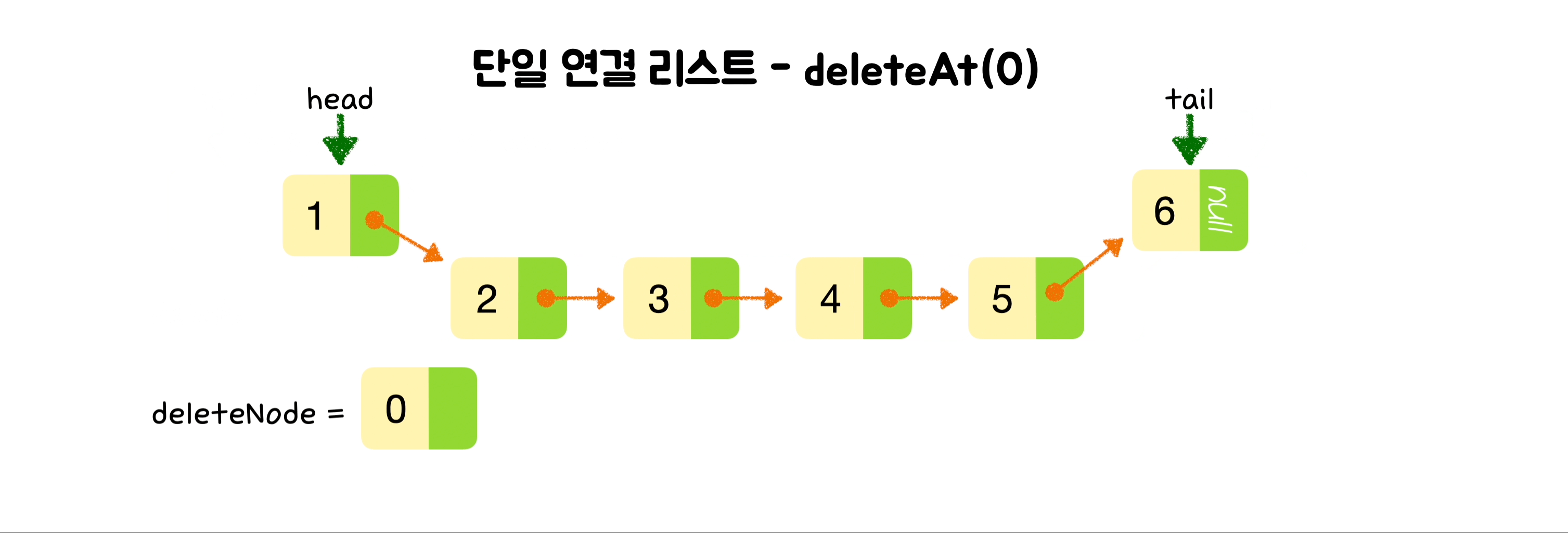
// 노드 삭제
  	deleteAt(index) {
      	// 범위를 벗어나는 노드 삭제를 요구하는 경우, 제거할 수 없다고 오류를 띄웁니다.
        if (index >= this.count || index < 0) {
            throw new Error('제거할 수 없습니다.🙅🏻‍♀️');
        }

        let curNode = this.head;
        if (index == 0) {
            let deletedNode = this.head;
            this.head = this.head.next;
            this.count--;
            return deletedNode;
        }

🕶️ 특정 위치의 노드 삭제

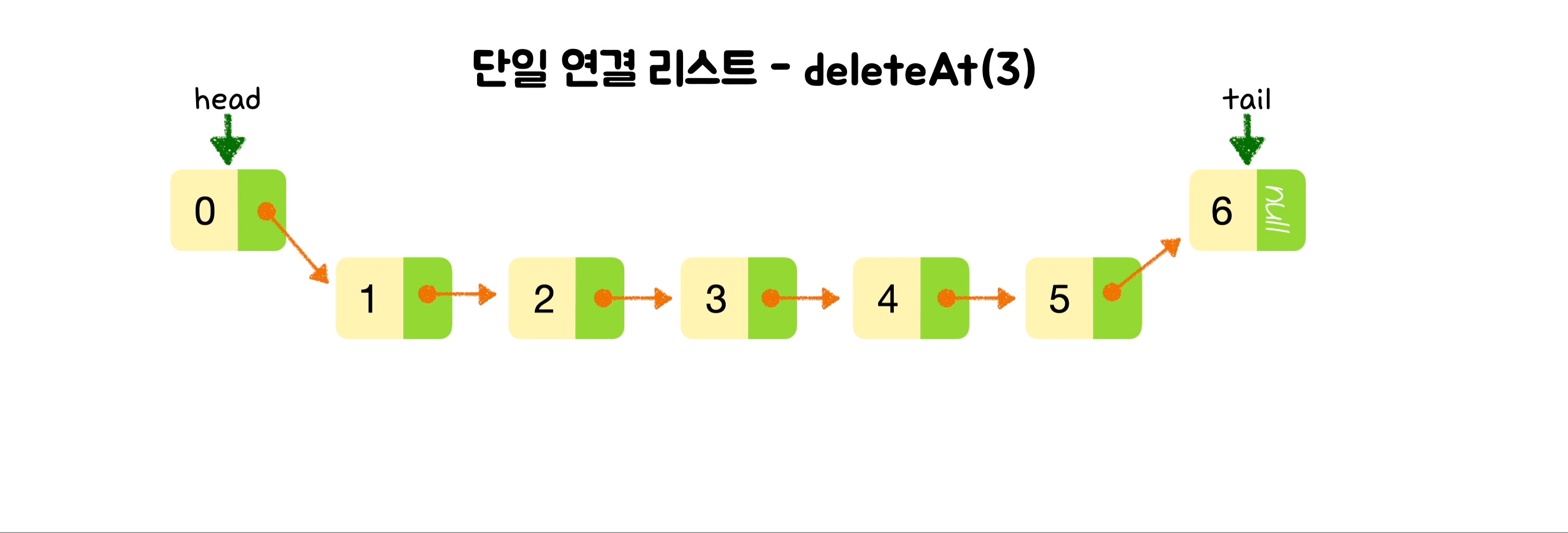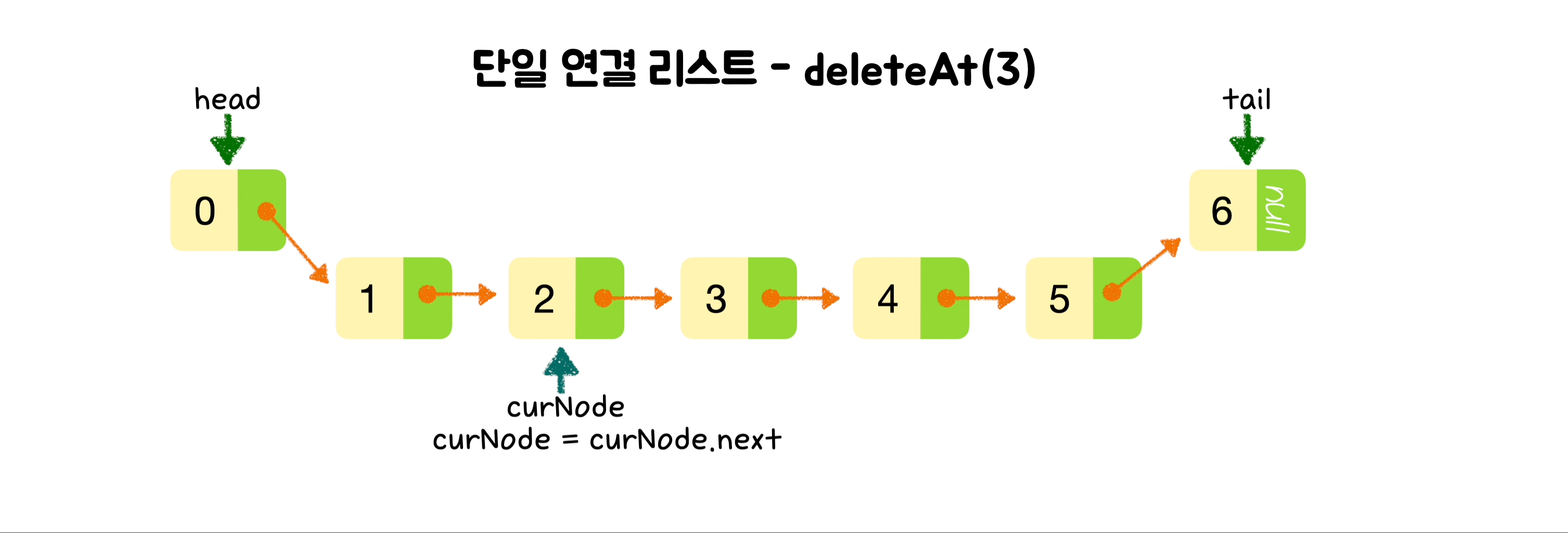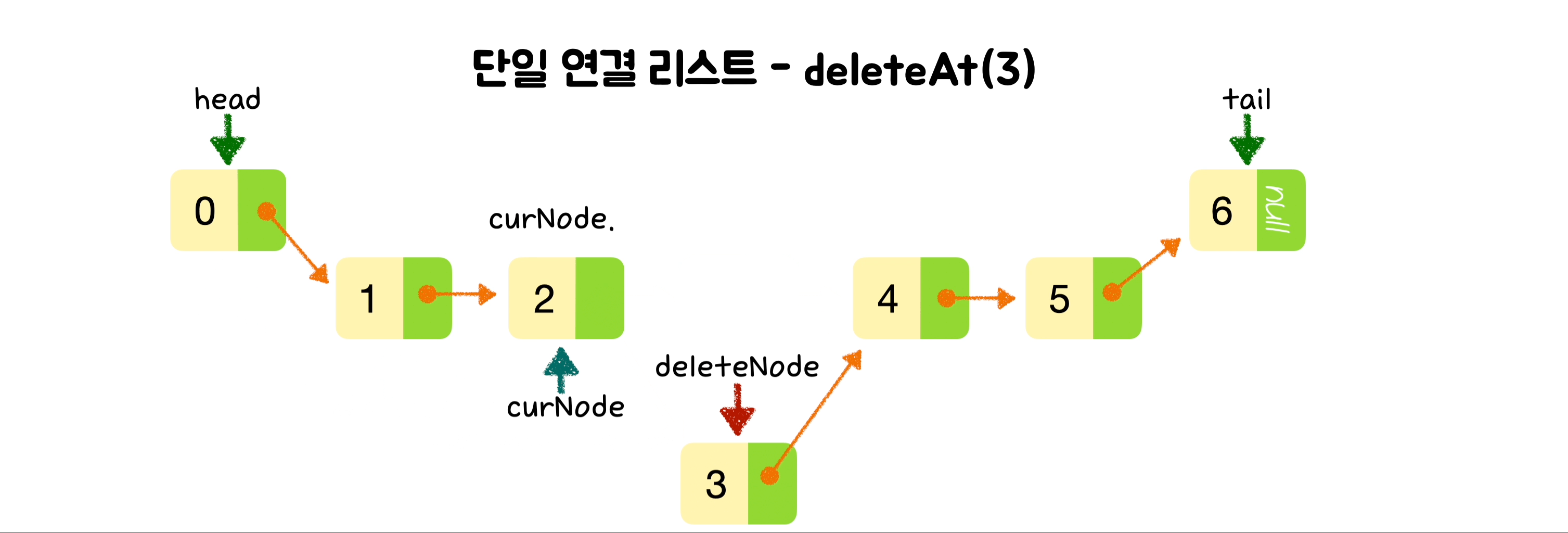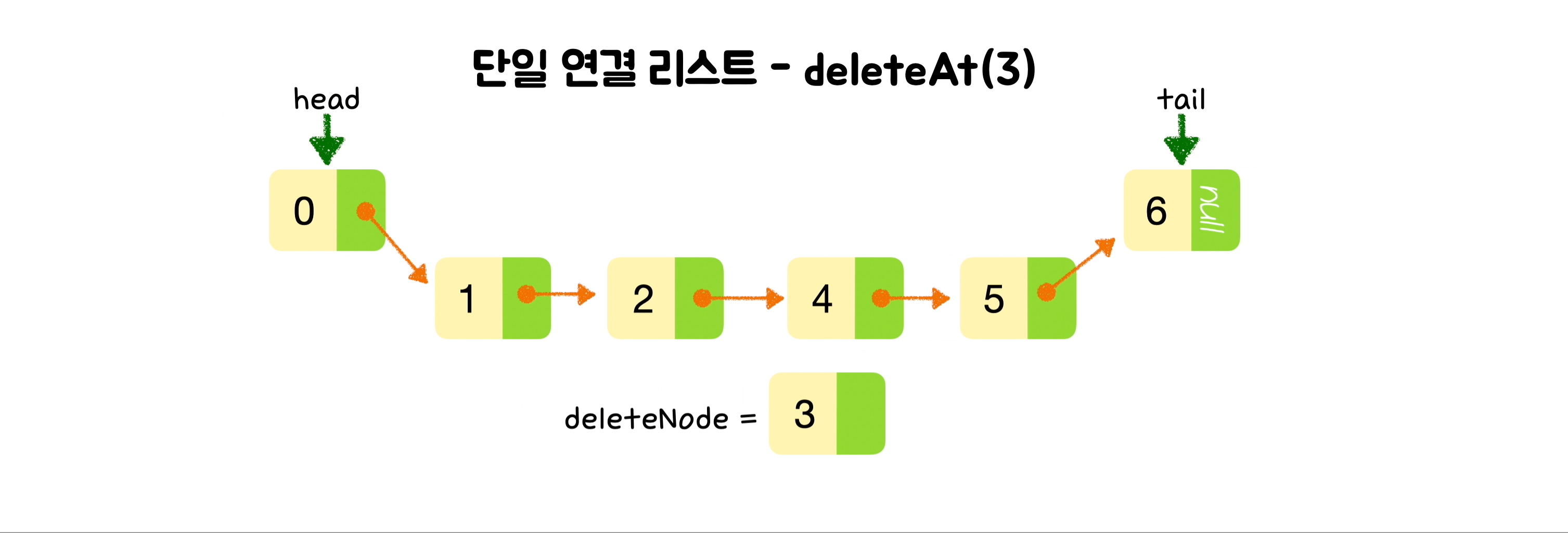
 	 else {
           for (let i = 0; i < index - 1; i++) {
               curNode = curNode.next;
           }
           let deletedNode = curNode.next;
           curNode.next = curNode.next.next;
           this.count--;
           return deletedNode;
       }
   }

   deleteLast() {
     	// daleteAt에 마지막 index를 넣어주어야 하므로 노드 갯수(===length)에서 1을 빼줍니다.
       return this.deleteAt(this.count - 1);
   }

🕶️ 연결 리스트 삭제 & 조회 & 프린트

  
  	// 전체 노드를 삭제합니다.
    clear() {
        this.head = null;
        this.count = 0;
    }
  
  	// 🔍 특정 노드의 값을 조회합니다.
    getNodeAt(index) {
        if (index >= this.count || index < 0) {
            throw new Error('범위를 넘어갔습니다.🤦🏻‍♀️');
        }
        let curNode = this.head;
        for (let i = 0; i < index; i++) {
            curNode = curNode.next;
        }
        return curNode.data;
    }
  
	// 🖨️ 전체 리스트를 보여줍니다.
    printAll() {
        let curNode = this.head;
        const printArr = [];

        while (curNode != null) {
          	printArr.push(curNode.data);
            curNode = curNode.next;
        }
        console.log(printArr);
    }
}

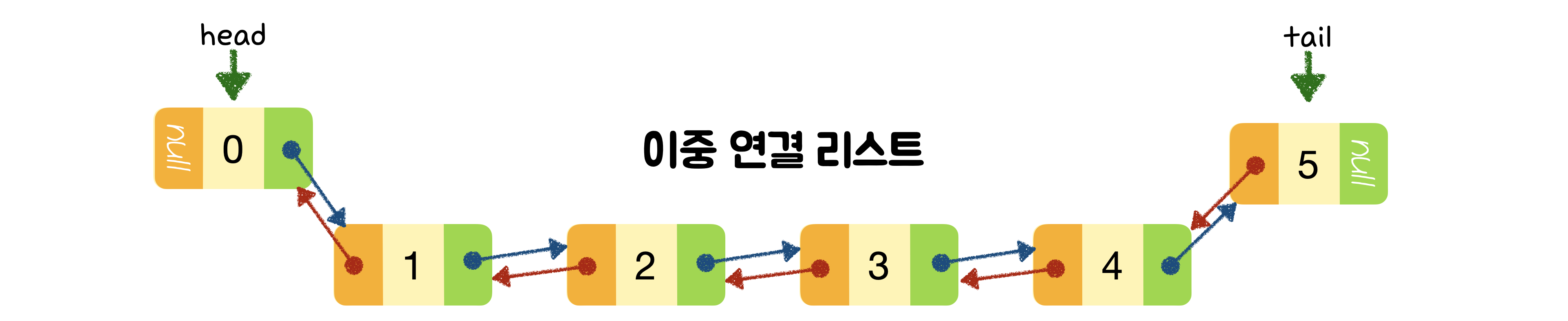
🪴 Dubly Linked List ( 이중 연결 리스트 )

• 데이터, 이전 노드의 주소, 다음 노드의 주소를 저장합니다. 단일 연결 리스트보다 더 많은 메모리를 차지합니다.

• 대신 이전 노드의 주소와 다음 노드의 주소를 모두 사용해 양방향으로 순회할 수 있습니다.

• 또한, 주어진 위치에서 삽입과 삭제의 복잡도는 O(n / 2) 입니다. 즉, O(n)입니다. 순회는 처음 혹은 끝에서 이루어질 수 있기 때문입니다.

🕶️ 노드 생성

class Node {
  constructor(data, prev = null, next = null) {
    this.data = data;
    this.prev = null;
    this.next = null;
  }
}

🕶️ 노드 삽입

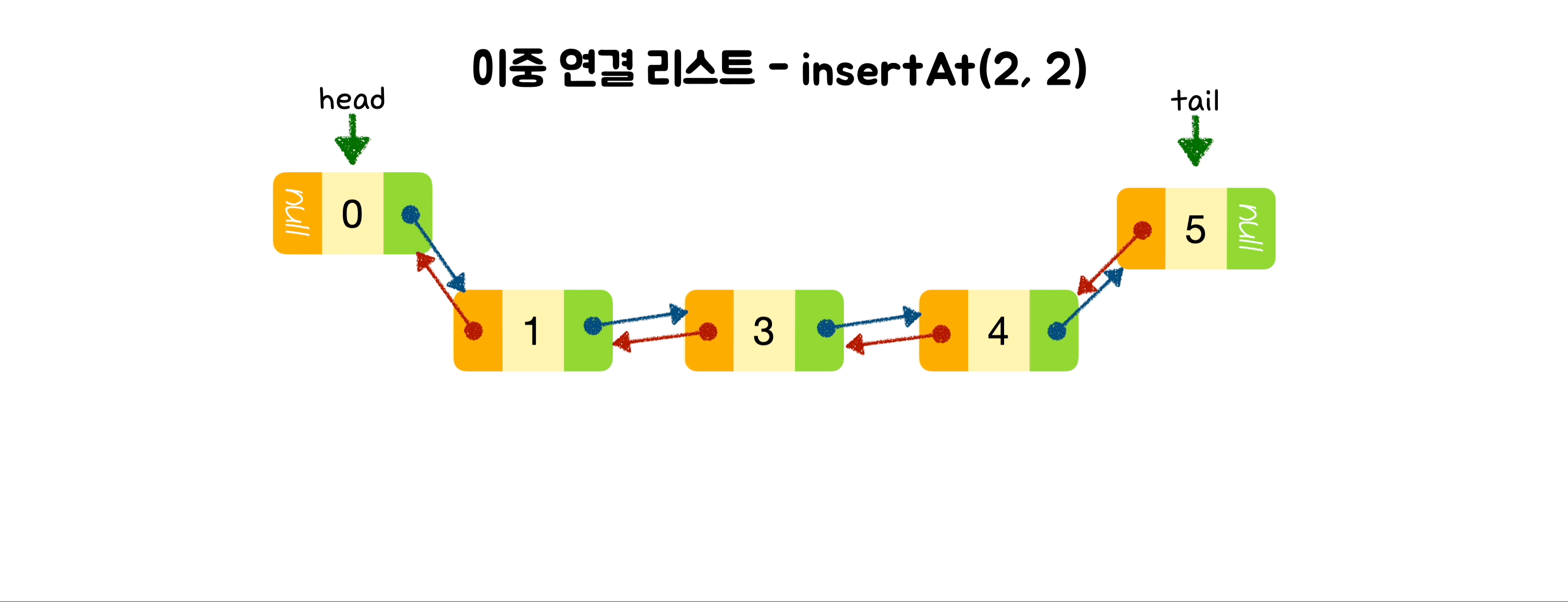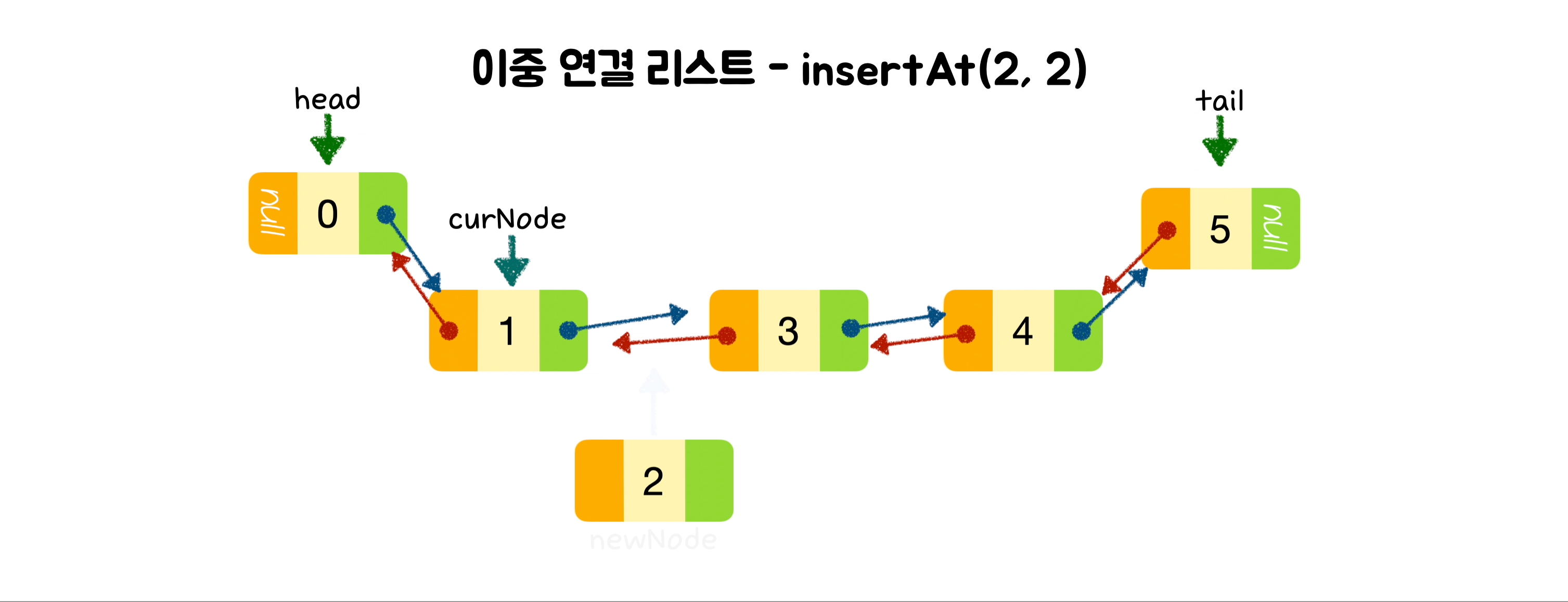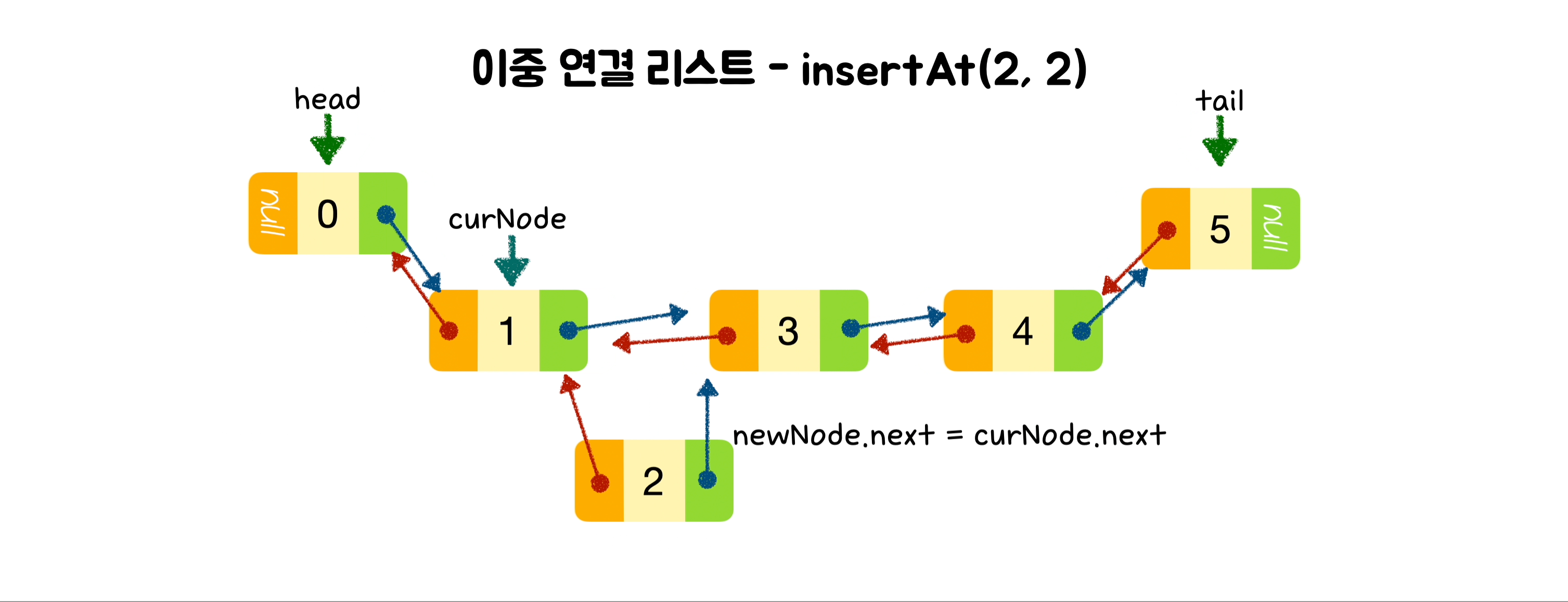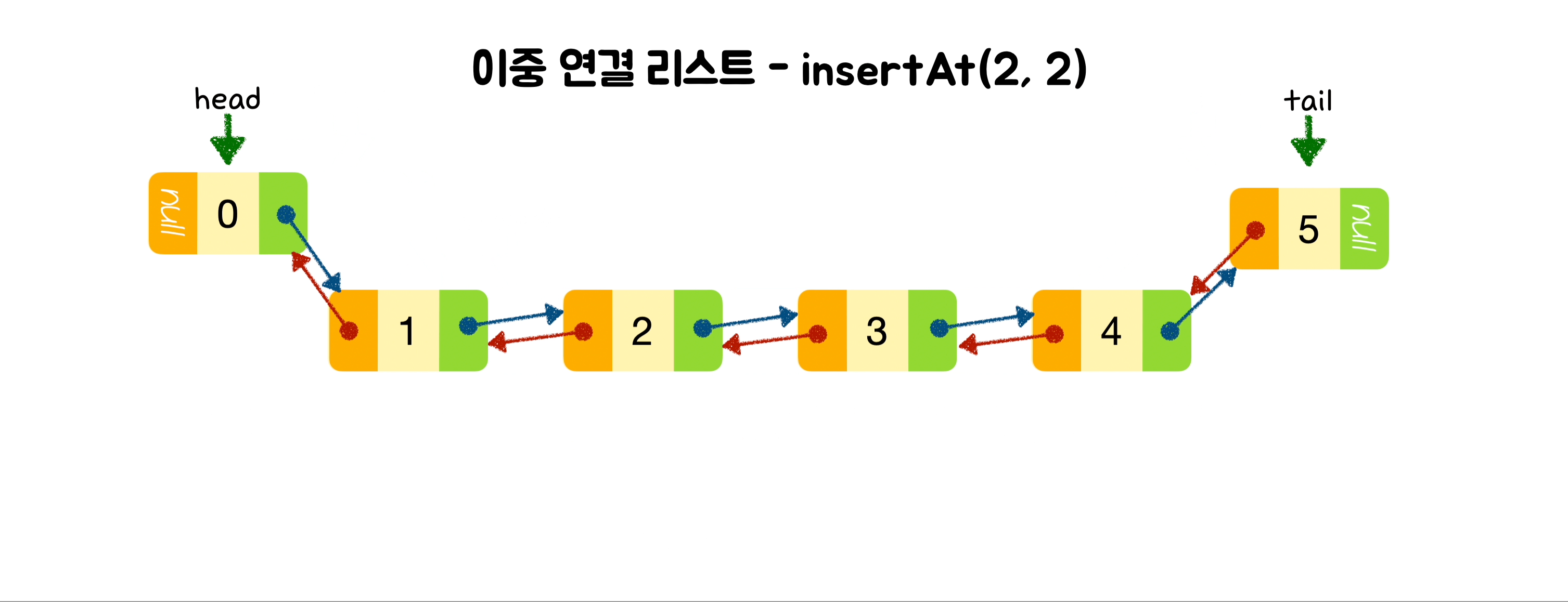
class DoublyLinkedList {
  constructor() {
    this.head = null;
    this.count = 0;
  }
  
  insertAt(index, value) {
        if (index > this.count || index < 0) {
            throw new Error('범위를 넘어갔습니다.🤦🏻‍♀️');
        }

        const newNode = new Node(value);
        if (index === 0) {
            newNode.next = this.head;
            newNode.prev = null;
            if (this.head !== null) {
                this.head.prev = newNode;
            }
            this.head = newNode;
        } else {
            let curNode = this.head;
            for (let i = 0; i < index - 1; i++) {
                curNode = curNode.next;
            }
            newNode.prev = curNode;
            newNode.next = curNode.next;
            curNode.next = newNode;
            curNode.next.prev = newNode;
        }
        this.count++;
    }
  
  insertLast(value) {
    this.insert(this.count, value);
  }

🕶️ 노드 삭제

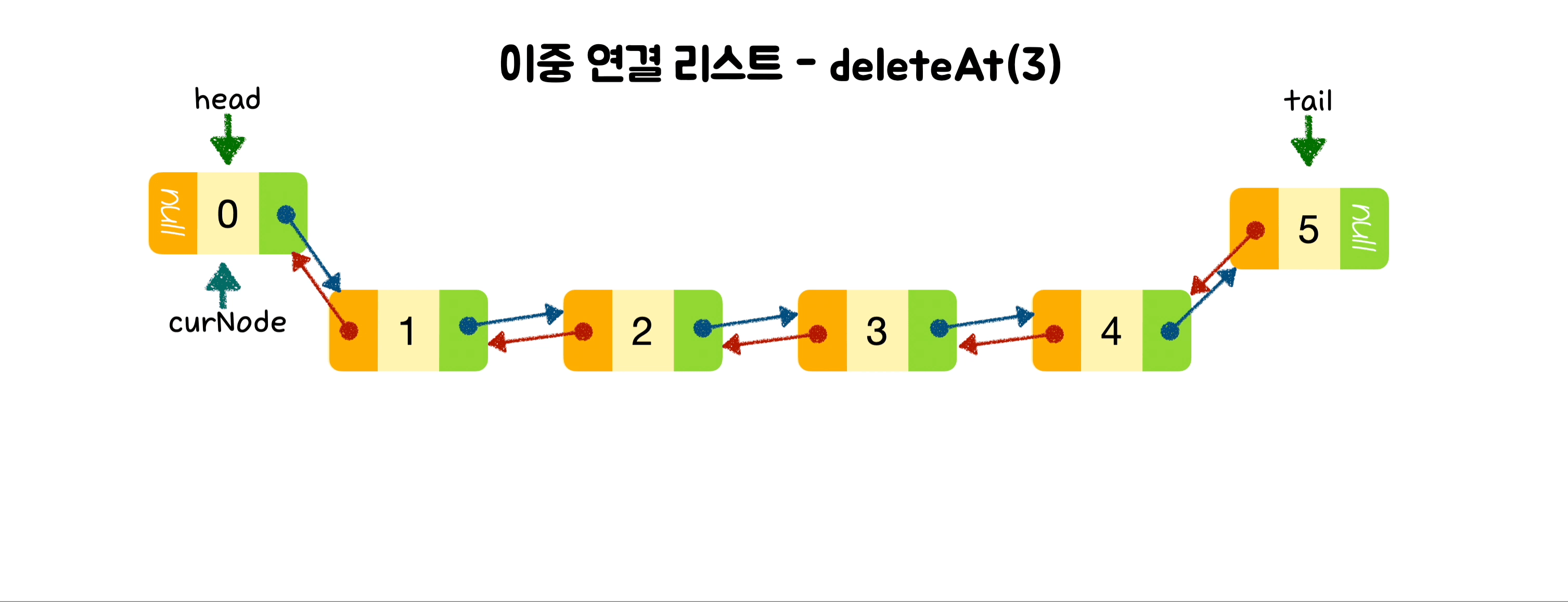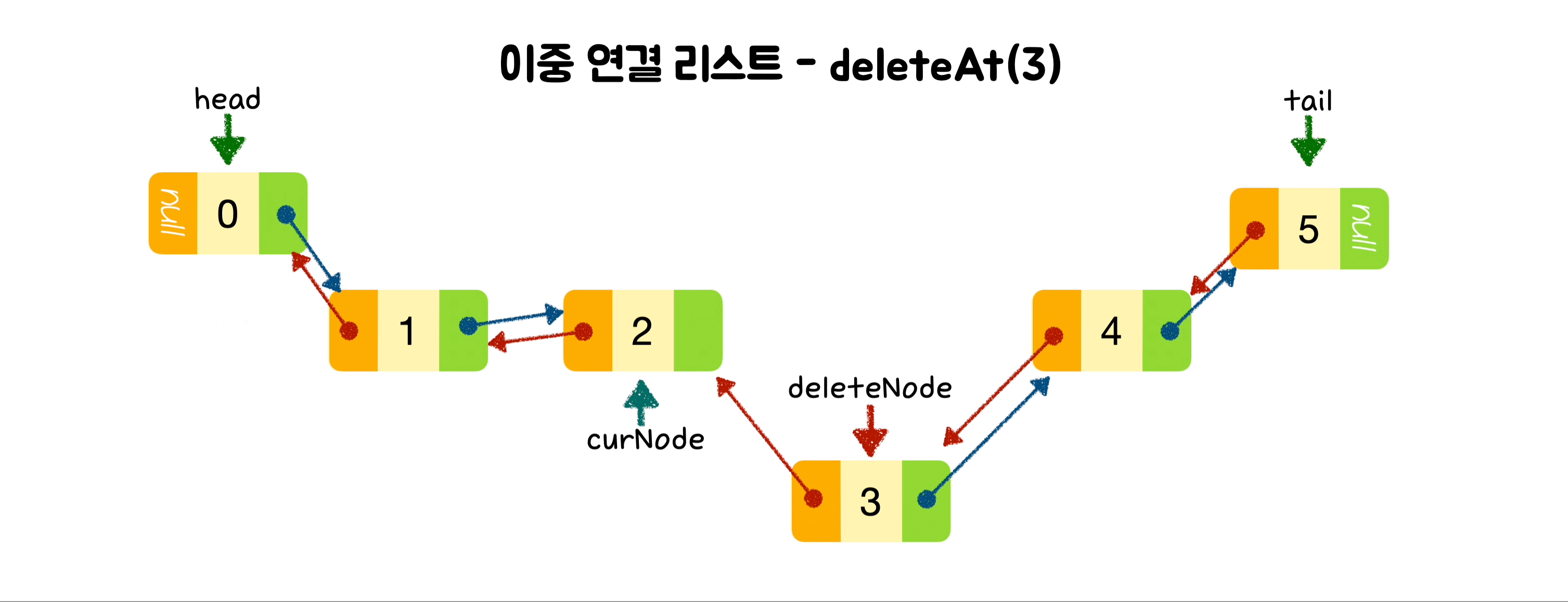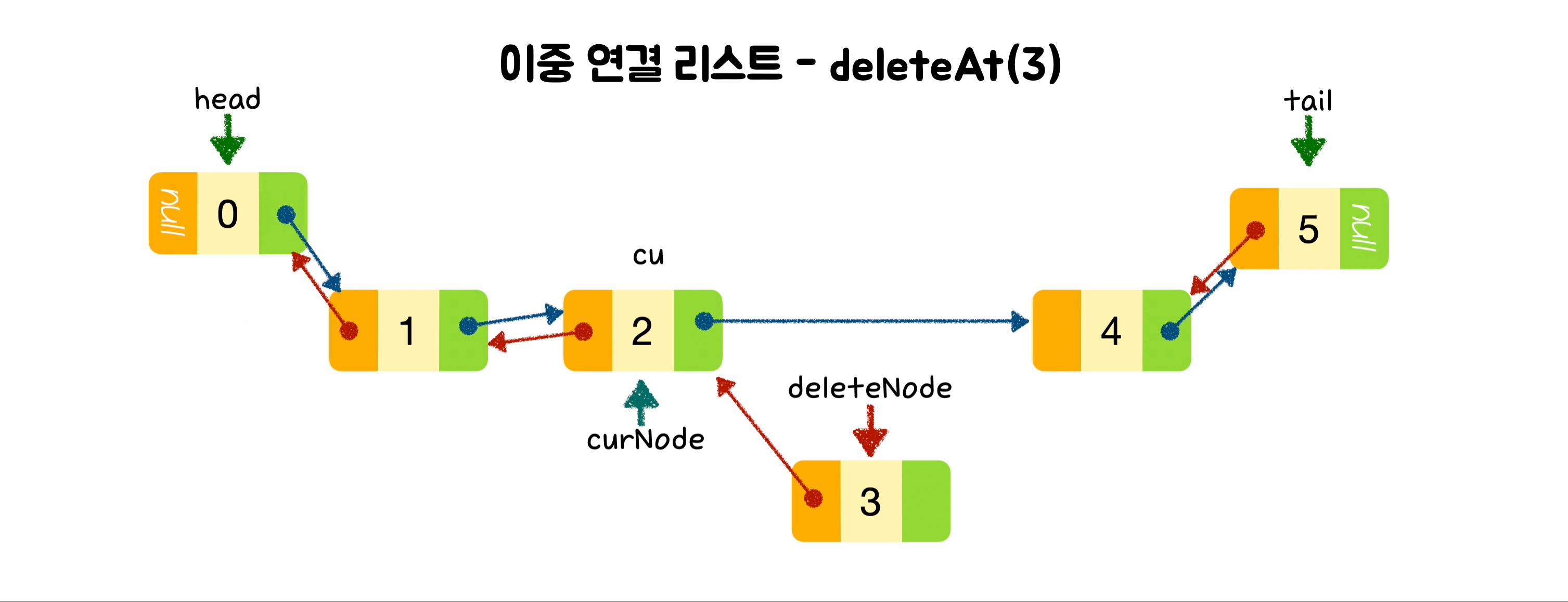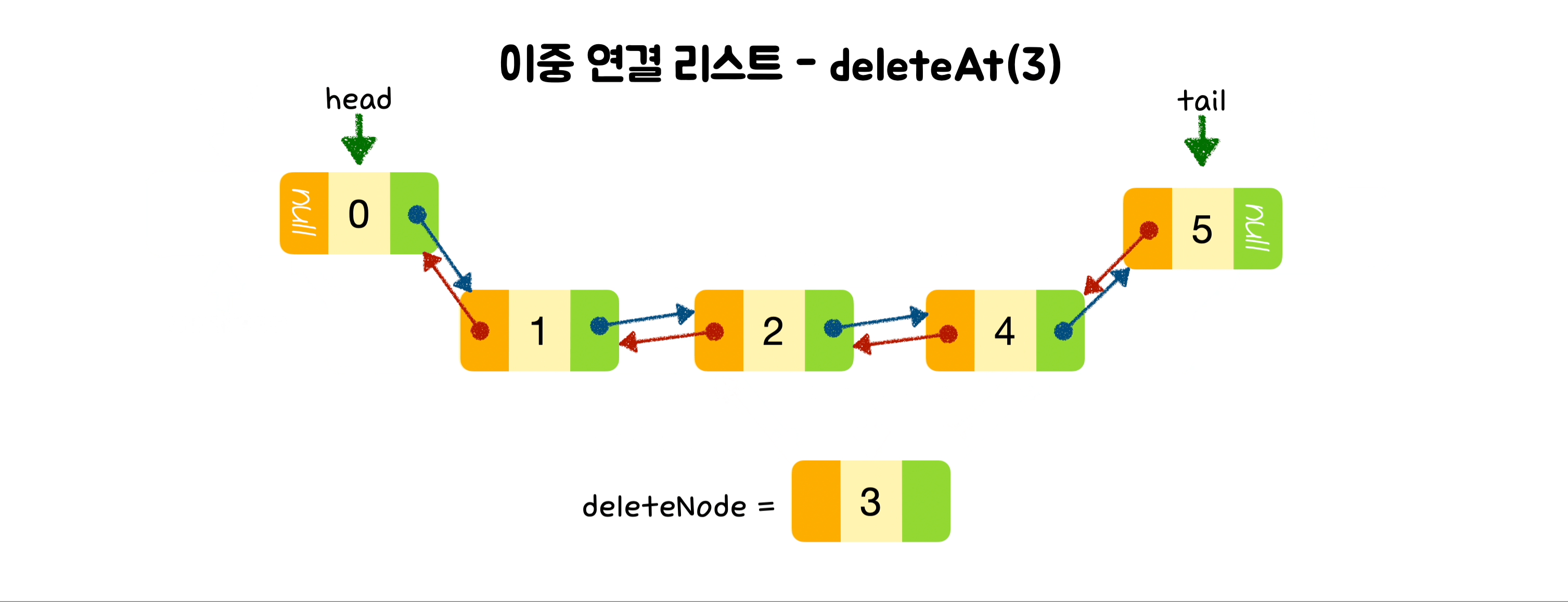
  deleteAt(index) {
        if (index >= this.count || index < 0) {
            throw new Error('제거할 수 없습니다.🙅🏻‍♀️');
        }

        let curNode = this.head;
        if (index === 0) {
            let deleteNode = this.head;
            this.head = this.head.next;
            this.head.prev = null;
            this.count--;
            return deleteNode;
        } else {
            for (let i = 0; i < index - 1; i++) {
                curNode = curNode.next;
            }
            let deleteNode = curNode.next;
            curNode.next = curNode.next.next;
            curNode.next.next.prev = curNode;
            return deleteNode;
        }
    }
  
  	deleteLast() {
        return this.deleteAt(this.count - 1);
    }

🪴 Circular Linked List ( 순환 연결 리스트 )

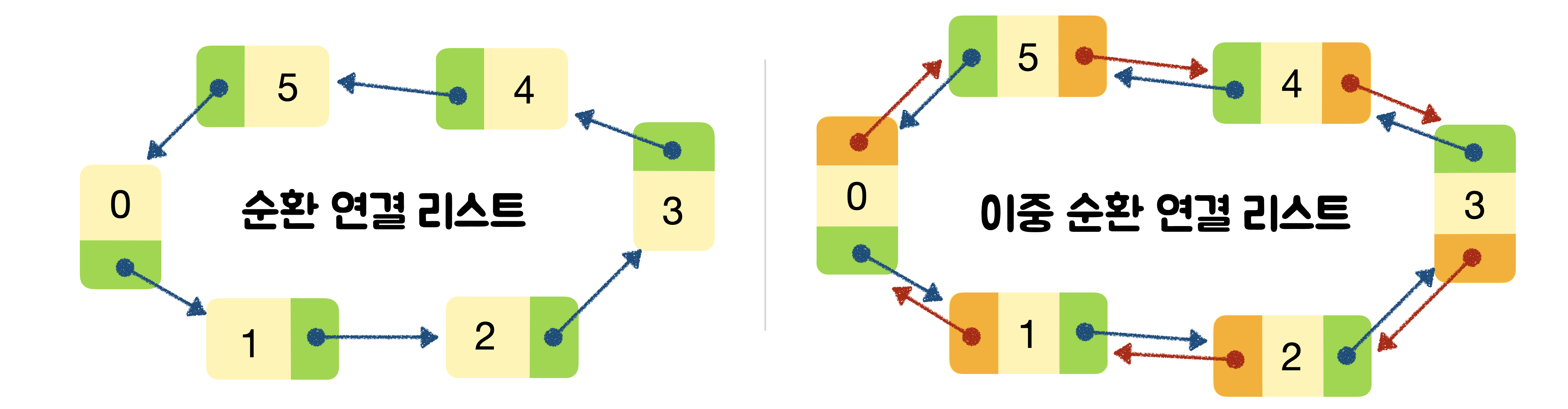
• 첫번째 노드와 마지막 노드가 서로 연결되어 원을 이루는 연결 리스트의 일종입니다. 연결 리스트의 끝은 null이 없습니다. 따라서 모든 노드가 시작점이 될 수 있고, 어느 지점에서든 시작하여 전체 목록을 탐색할 수 있고 처음 방문한 노드를 다시 방문할 때 중지하면 됩니다.

• 두 개의 포인터를 유지할 필요가 없습니다. 마지막으로 삽입된 노드에 대한 포인터를 유지할 수 있으며, 앞부분은 항상 마지막 노드 다음으로 알 수 있습니다.

• 리스트를 반복적으로 탐색하는 애플리케이션에 유용합니다. 여러 응용 프로그램이 PC에서 실행 중인 경우 운영 체제는 실행 중인 응용 프로그램을 목록에 넣은 다음 순환하여 각 응용 프로그램에 실행할 시간을 제공한 다음 잠시 기다리게 하는 것이 일반적입니다. command+tap (window에서는 alt + tap)으로 실행 중인 응용 프로그램을 전환할 때 사용됩니다.

• 다만, 다른 연결 리스트에 비해 더 복잡하고 코드를 주의 깊게 처리하지 않으면 무한 루프에 빠질 수 있습니다. 또 특정 응용 프로그램에서 효율적일 수 있지만 목록을 정렬하거나 검색해야 하는 경우와 같은 특정한 경우에는 다른 데이터 구조보다 성능이 느려질 수 있으므로 사용에 유의해야 합니다.

👀 Reference

• Linked List – Data Structure and Algorithm Tutorials
• Wiki - 연결리스트