[ ᴀʟɢᴏʀɪᴛʜᴍ ] Radix Sort ( 기수 정렬 )

NewHa·2023년 9월 7일
algorithm
1

ᴀʟɢᴏʀɪᴛʜᴍ

목록 보기
7/14
post-thumbnail

🌱 Radix Sort ( 기수 정렬 )

👉🏻 기수 정렬 (基數整列, Radix Sort) : 기수 별로 비교 없이 수행하는 선형 정렬 알고리즘입니다. 기수란 주어진 데이터를 구성하는 기본요소로 자릿값 개념을 활용하는 것입니다. 정수라면 숫자의 자릿값마다 숫자별로 정렬한다는 것입니다. 기수정렬은 정수, 문자열, 천공카드 등 다양한 자료에서 사용이 가능하지만 정렬하려는 배열이 크기가 유한하고 사전순으로 정렬이 가능한 요소만 있어야 한다는 한계를 가집니다.

기수정렬은 기수에 따라 원소를 버킷에 집어넣기 때문에 비교 연산이 불필요하다는 특성을 가집니다. 쉽게 말하자면, 다른 정렬과 달리 비교 작업을 수행하지 않는다는 것입니다. 요소를 직접 비교하는 대신 각 숫자의 자릿값을 기준으로 요소를 버킷에 삽입해 모든 숫자 요소에 대해 수행될 때까지 각 자릿수를 반복해서 정렬해 최종 정렬 순서를 달성합니다. (이 때 반복할 때마다 기수의 도메인 크기만큼의 누적합이 요구된다고 하는데.. 나중에 누적합을 공부한 후 풀어 설명하겠습니다.)

버킷은 말 그대로 양동이에 담는 것 처럼 요소를 정렬할 것들로 분할해서 담는다는 의미입니다. (더 자세한 내용은 다음 버킷정렬에서 설명하겠습니다.) 각 위치에서 안정적인 알고리즘을 사용해야 합니다.

☀️ characteristic of Radix Sort ( 특징 )

🙆🏻‍♀️ 장 점

  • 비교 작업을 수행하지 않고 선형 시간 복잡도를 가지므로, 대규모 데이터 세트에 대한 퀵 정렬 및 병합 정렬과 같은 비교 기반 정렬 알고리즘보다 빠릅니다.

  • 동일한 키 값을 가진 요소는 정렬된 출력에서 상대적 순서를 유지하는 안정적인 알고리즘입니다. 하나에 버킷에 둘 이상의 데이터가 들어가는 경우, 들어간 순서대로 꺼내기 위해 큐 자료구조를 사용합니다.

  • 많은 수의 정수나 문자열을 정렬하는 데 매우 효율적인 알고리즘입니다. ( 고정 크기 키를 사용하므로 )

  • 많은 접미사 배열 구성 알고리즘에서 사용되고, 요소의 숫자가 작으면 패스 횟수가 작아져서 더욱 효율적입니다.

🙅🏻‍♀️ 단 점

  • 부동 소수점 실수처럼 특수한 비교 연산이 필요한 기타 유형의 데이터를 정렬하는 데는 비효율적입니다.

  • 임시 카운트 배열을 사용해 각 숫자 값이 나타나는 횟수를 저장하므로 내부 알고리즘이 아니며, 이로 인해 많은 양의 메모리가 필요해집니다.

  • 소규모 데이터 셋이나 고유 키 수가 적은 데이터 셋에서는 효율적이지 않습니다. 또한 길이가 다른 데이터들을 대상으로는 사용하기 어렵습니다. 길이가 각각 다를 경우 빈 공간을 메꾸는 추가 작업이 발생해 성능이 저하됩니다. 즉, 기수 정렬은 사용할 수 있는 데이터에 한계를 가집니다. (하지만 정렬의 대상 및 기준에 따라 특정 알고리즘을 적용하면 길이가 다른 데이터도 정렬이 가능해집니다.)

  • 버킷의 갯수가 정해져 있지 않습니다. 데이터에 따라 데이터 전체 크기에 기수 데이블 만큼의 메모리를 요해 때때로 필요로 한 것보다 더 많은 메모리를 소비합니다.

  • 숫자나 문자를 기반으로 하므로 전체 데이터를 미리 알아야해서 유연성이 떨어집니다.

☀️ Operations of Radix Sort ( 작동 )

정수로 이루어진 배열을 정렬하는 예를 그려보았습니다.

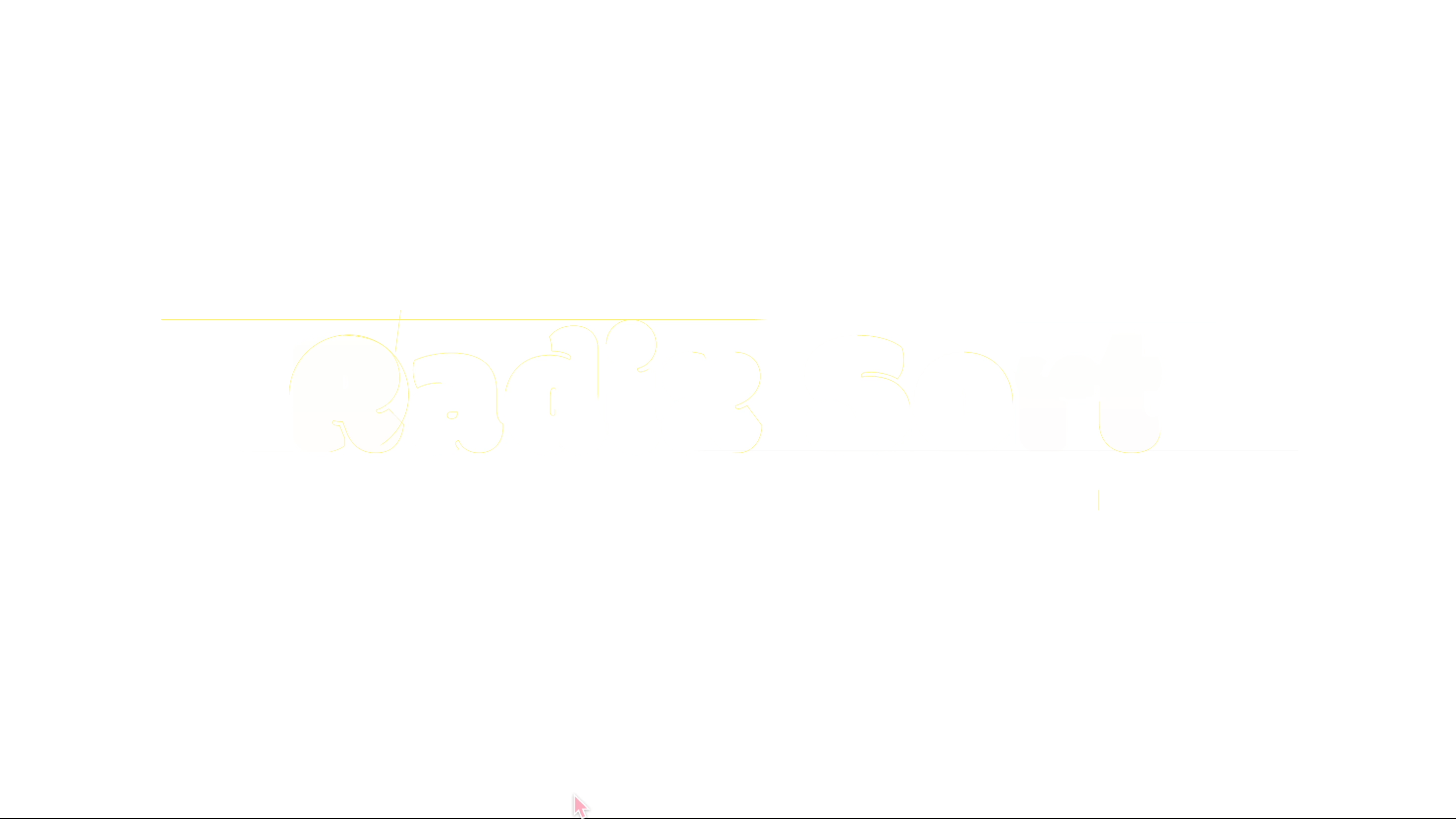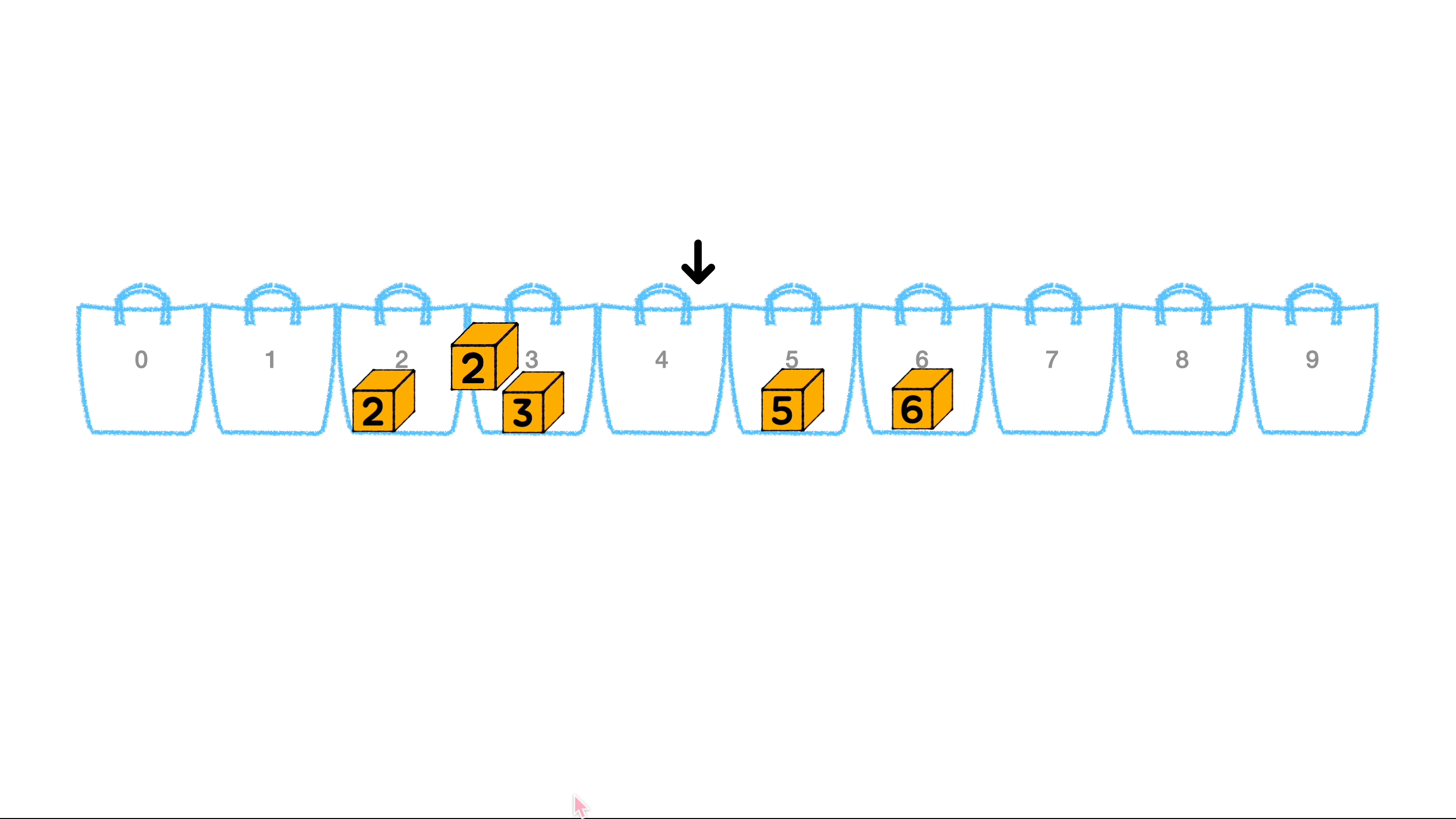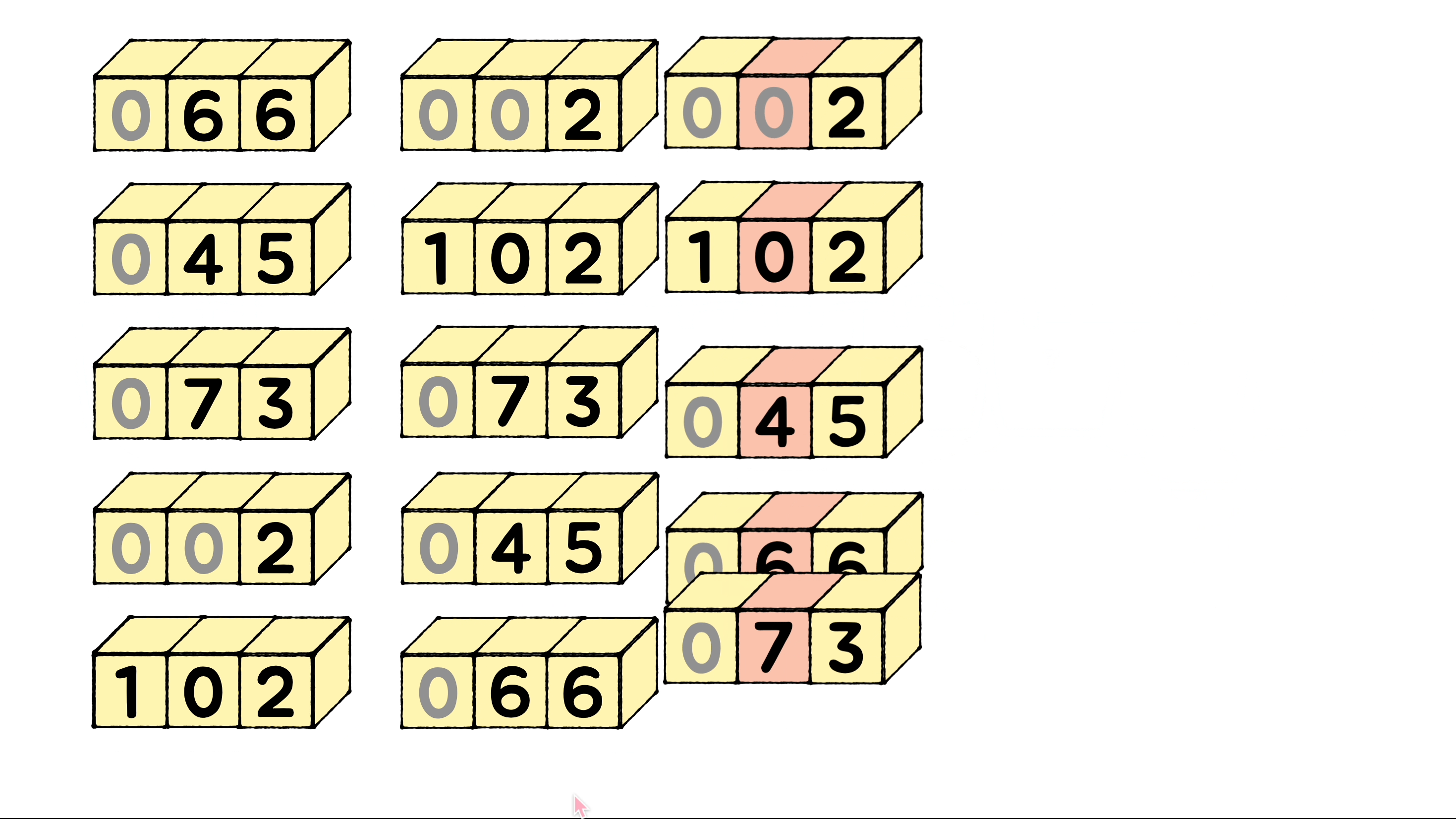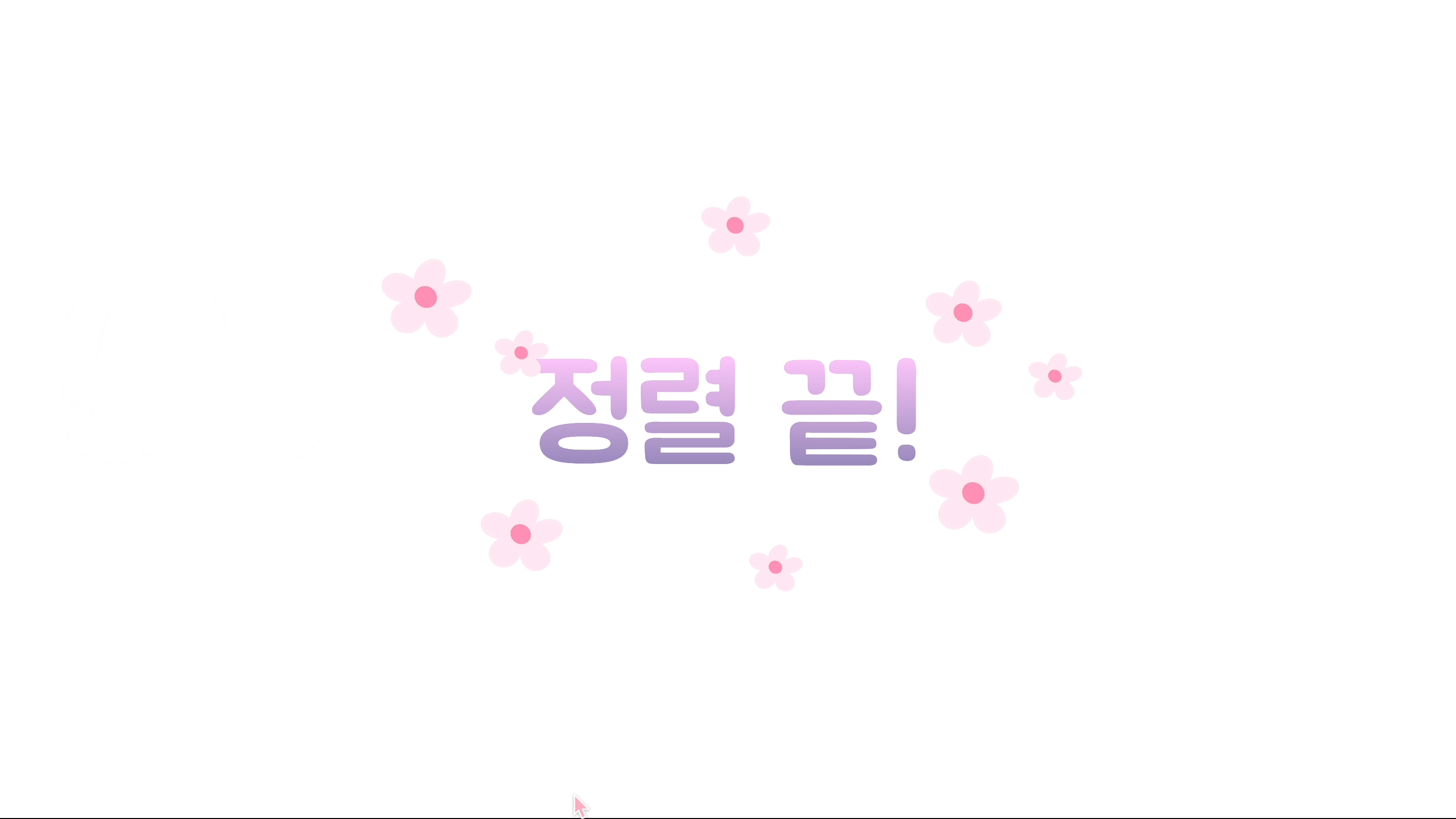
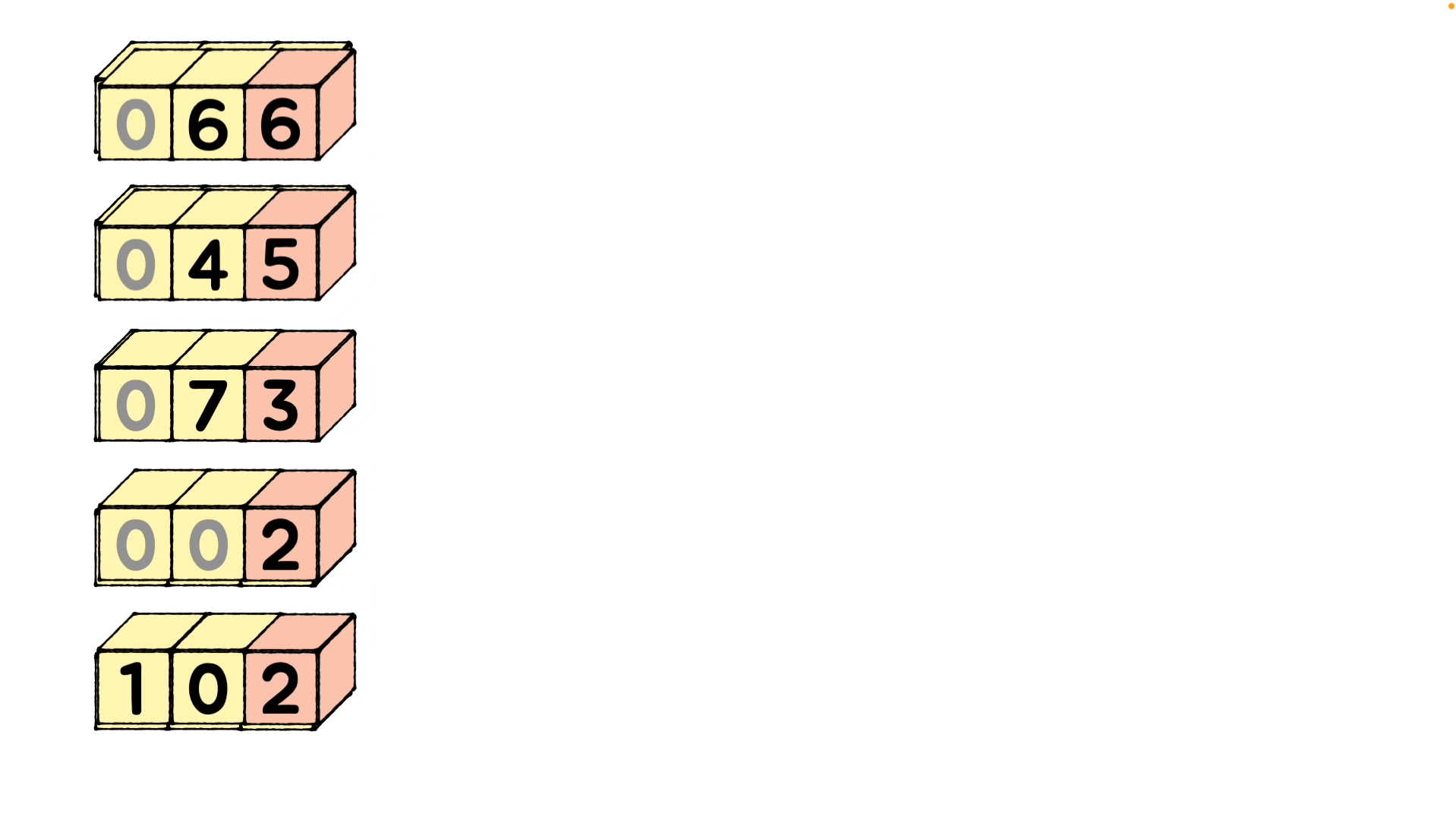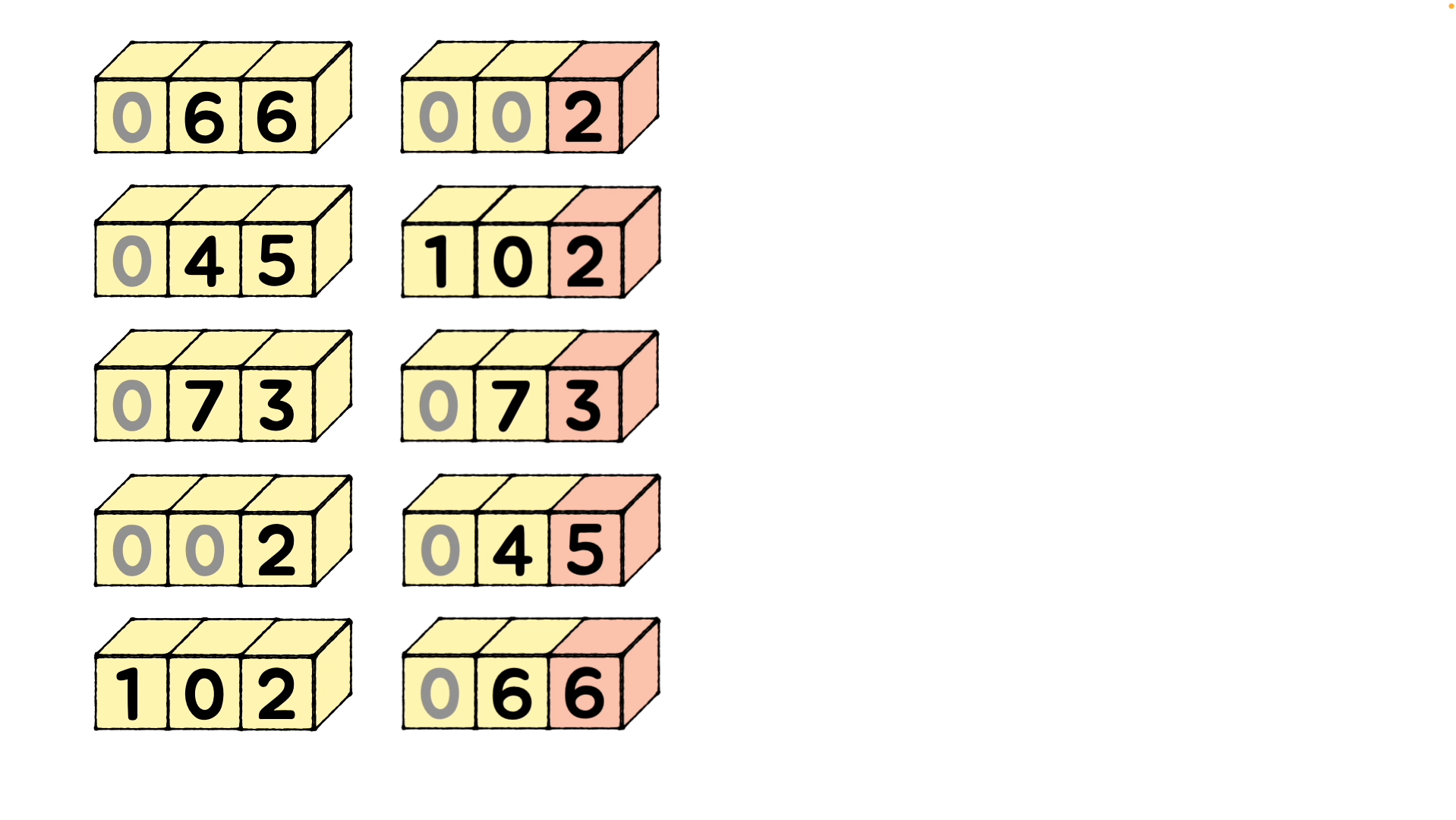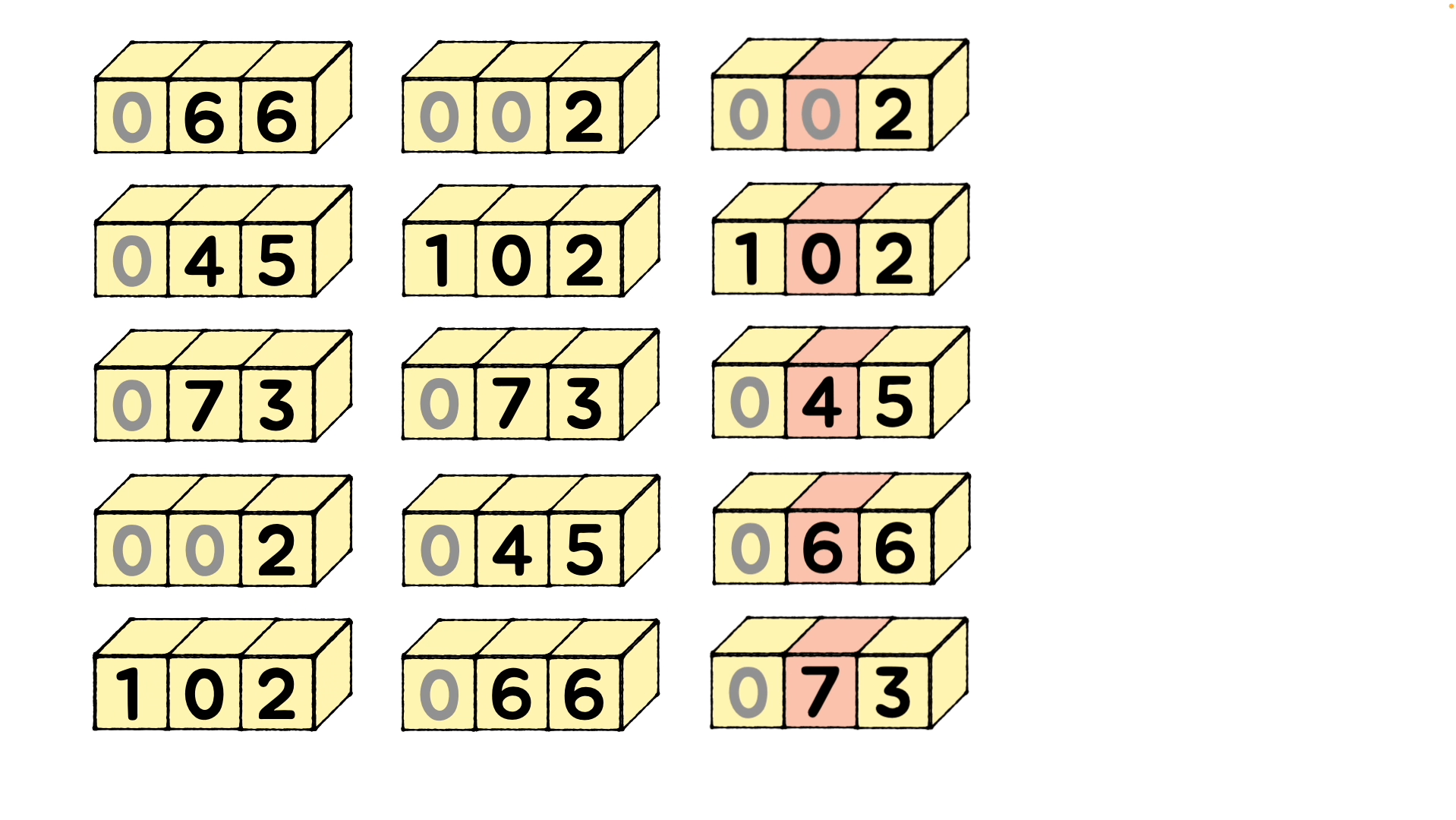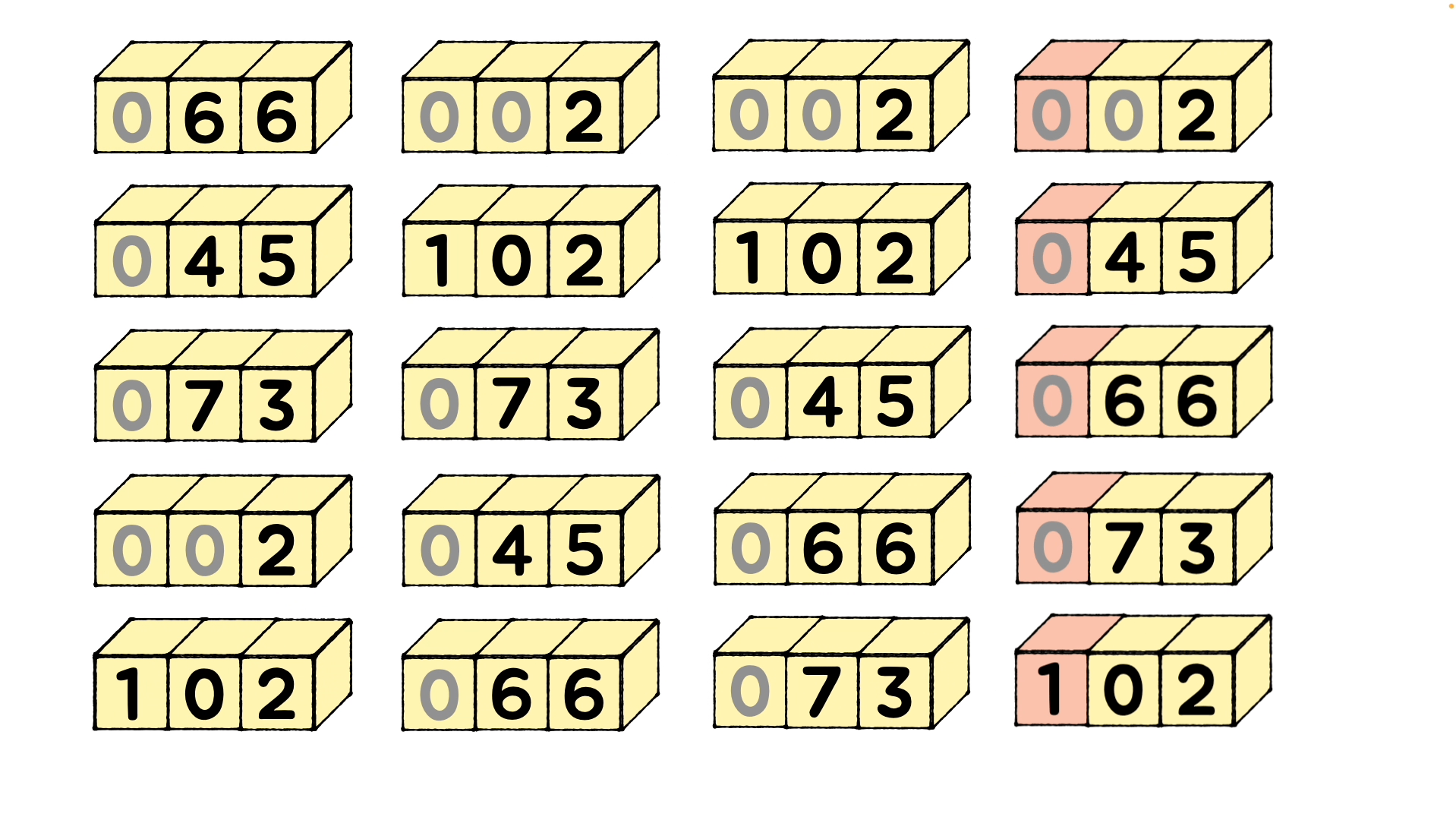
  • 배열의 모든 요소의 자릿수가 동일한지 확인하고, 동일하지 않은 경우 배열에서 가장 큰 요소(102)를 찾아 나머지 요소에 내부적으로 0을 사용해 자릿수를 동일하게 맞춰줍니다.

  • 진수에 따라 버킷의 갯수를 정해야 합니다. 10진수라면 숫자는 0 ~ 9 사이에 속하므로 10개의 버킷을 가져오고, 문자열이라면 a ~ z (26개) 범위 내이므로 0~ 25개의 버킷을 고려합니다. 각 버킷에 숫자를 배치하고 버킷을 연결해 빈 배열을 만듭니다.

  • 자릿수를 기준으로 요소를 정렬하기 시작합니다. 위 사진에 예시에 따르면 1의 자리 숫자를 기준으로 버킷에 넣어 정렬해줍니다. 그림에서는 이 부분입니다.

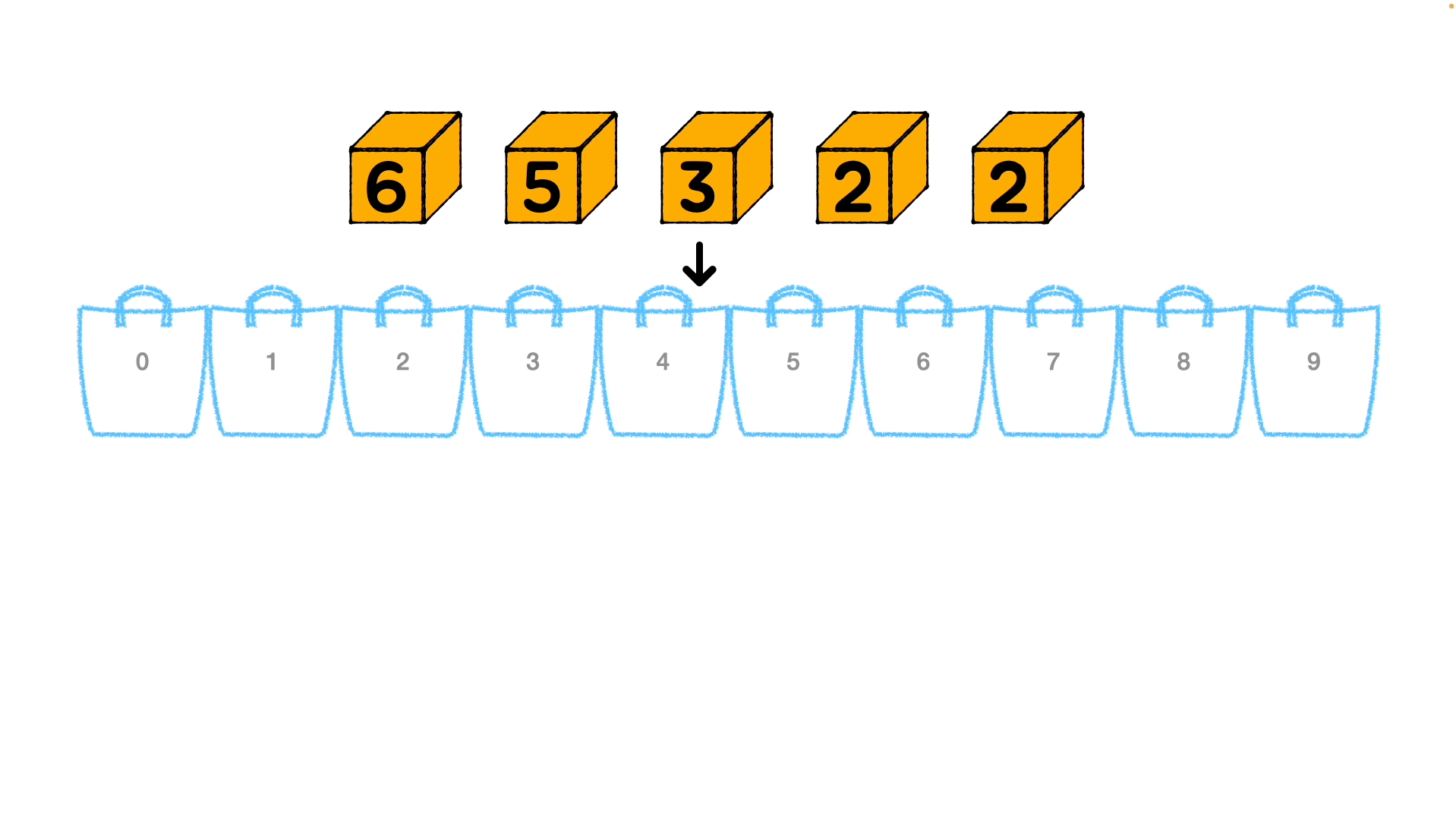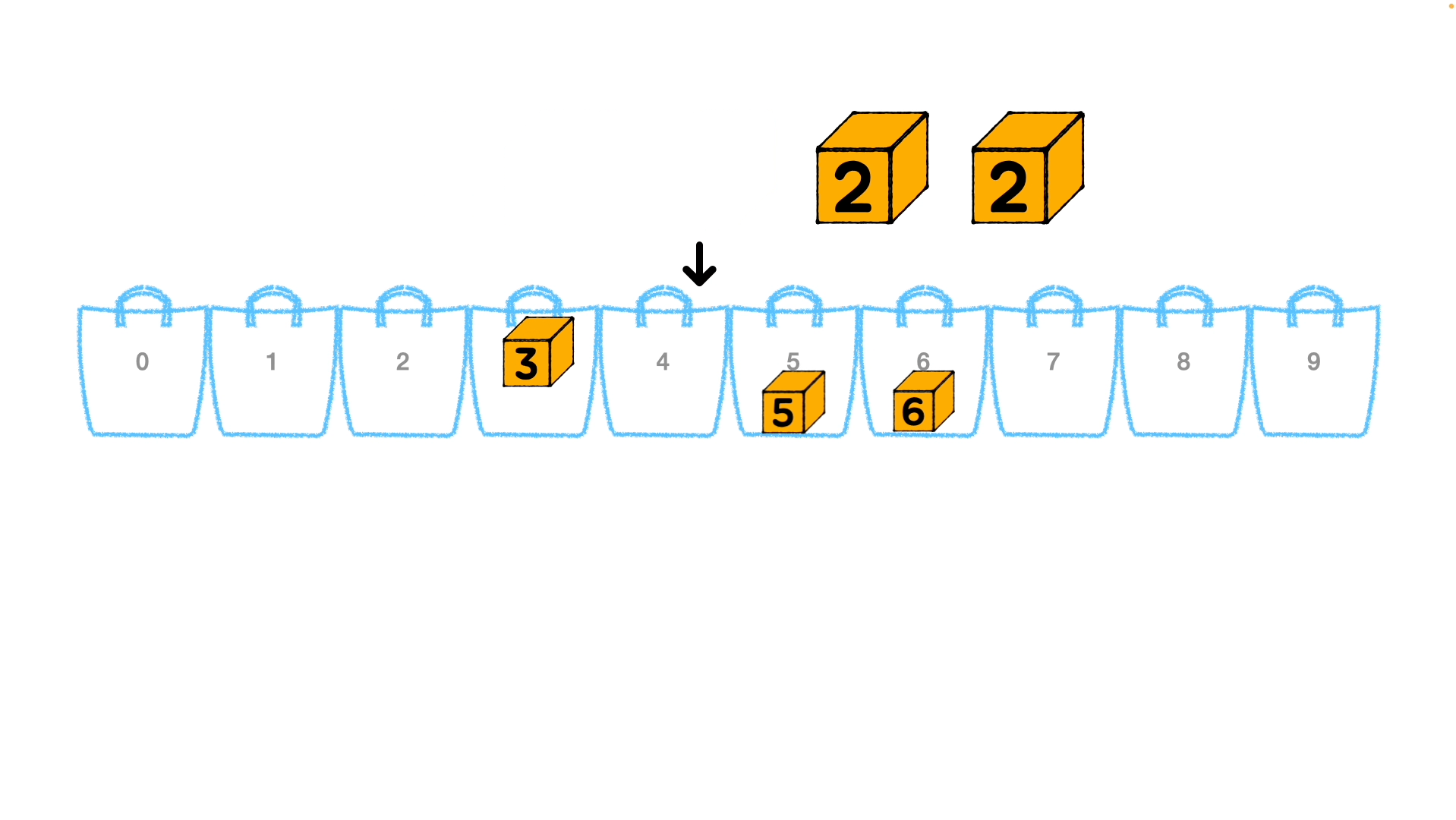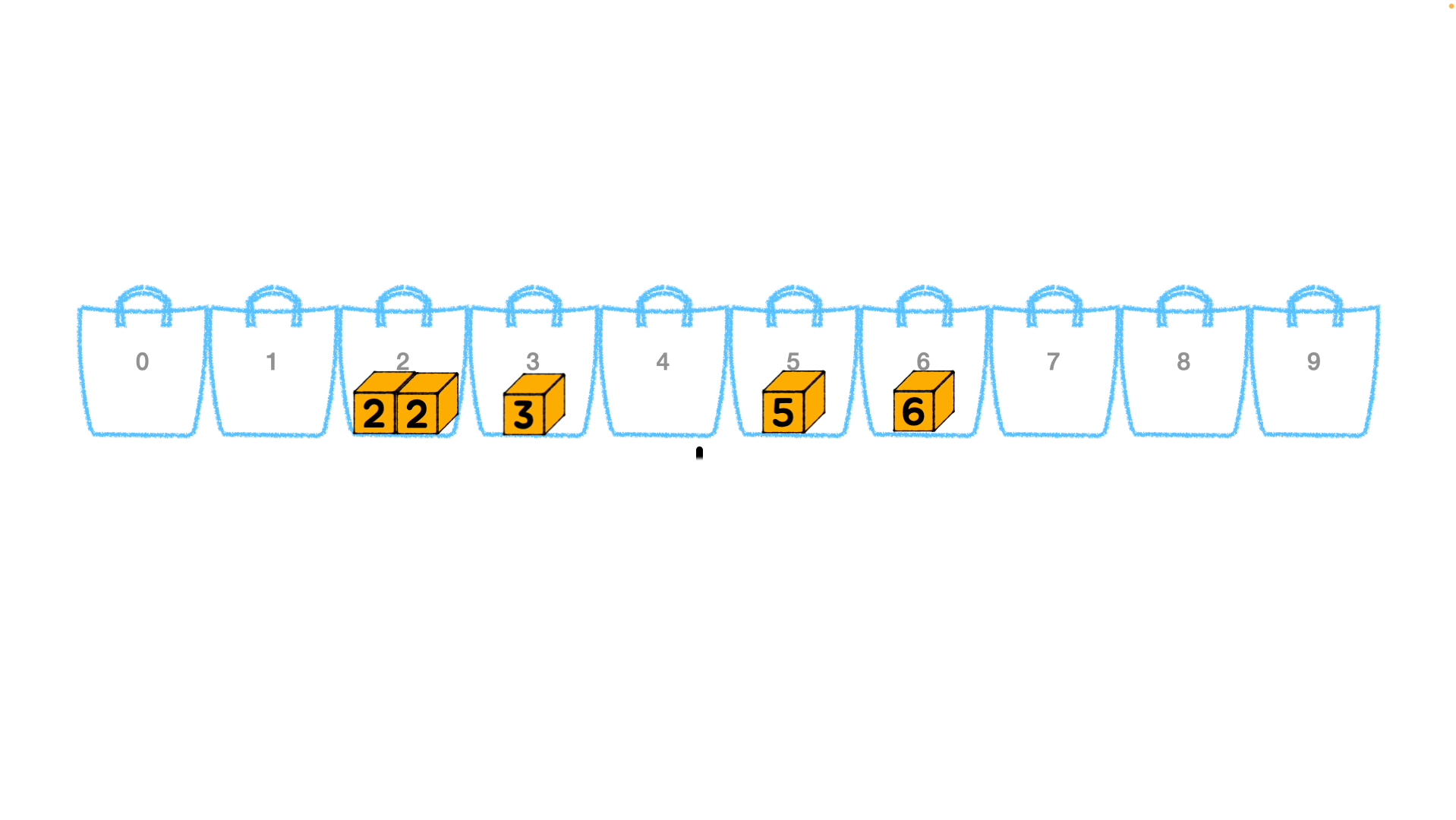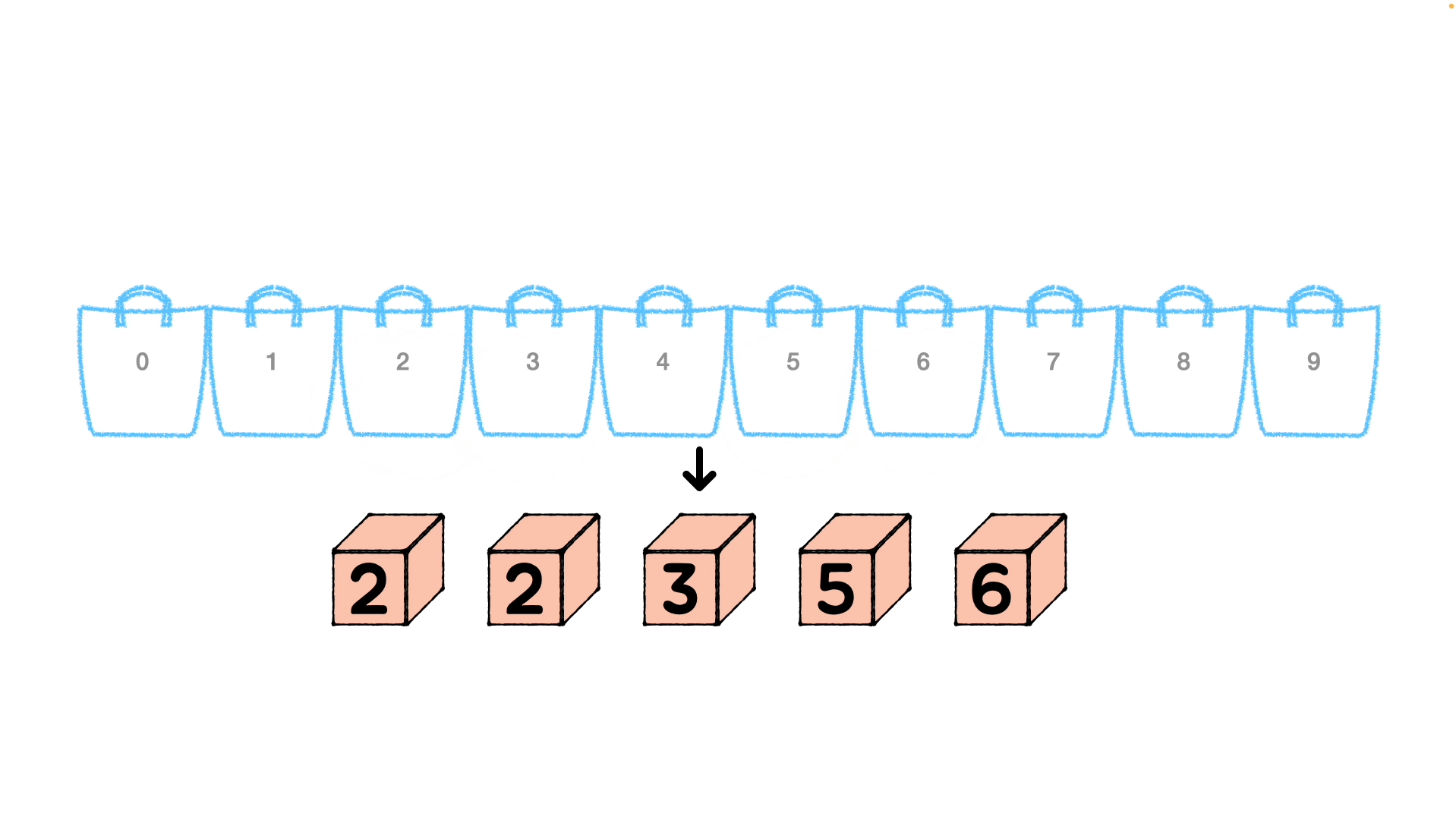
0 ~ 9 까지 버킷 번호에 각 숫자들이 자리를 찾아 배치되며 정렬되어 나옵니다. (버킷 내에서 정렬되는 것이 아닙니다.) 그렇게 1의 자리수 [6, 5, 3, 2, 2]를 오름차순으로 정렬하여 [2, 2, 3, 5, 6] 이 되고, 이를 기준으로 계수를 정렬하면 [2, 102, 73, 45, 66] 이 됩니다.

  • 10의 자리와 100의 자리에서도 동일한 정렬을 반복하여 정렬을 완료합니다.

🌿 How to radix sort of LSD, MSD

MSD ( Most Significant Digit )

  • 가장 큰 자릿수부터 정렬을 진행해 나가는 방식입니다. 쉽게 말하자면 정수를 기준으로 왼쪽 자릿수(가장 큰 자릿수)부터 정렬해 나갑니다. 완전히 정렬되기 전에도 중간에 정렬이 완료될 수 있습니다. 대신 중간에 데이터를 점검해야 해서 구현이 복잡합니다.
  • MSD는 길이가 정해지지 않은 문자열을 정리하는 데에 사용할 수 있습니다. 안정적이거나 불안정해질 수 있고, 임의의 문자열로 작동할 수 있습니다.
  • 최선의 경우 O(n) / 최악의 경우 O(k * n) 의 시간복잡도를 가집니다.

    👆🏻 정렬이 진행되고 있는 과정을 알기 쉽습니다.

LSD ( Least Significant Digit )

  • 가장 작은 자릿수부터 정렬을 진행해 나가는 방식입니다. 쉽게 말하자면 정수를 기준으로 오른쪽 자릿수(1의 자리)부터 정렬해 나갑니다. 완전히 정렬되기 전에는 결과를 알 수 없지만 대신에 구현이 간단합니다. 일반적인 기수 정렬의 구현은 LSD방식으로 구현하고 있습니다.
  • 올바르게 작동하려면 안정적이어야해, 길이가 정해지지 않은 문자열 등에서는 사용하기 어렵습니다.
  • 최선의 경우에도, 최악의 경우에도 O(k * n)의 시간복잡도를 가집니다.

    👆🏻 정렬이 진행되고 있는 과정을 알기 어렵습니다.

☀️ Implement of Radix Sort ( 구현 )

구현의 편의상 일반적으로 기수정렬은 LSD 방식을 기준으로 합니다. LSD와 MSD 방식 간 성능차이는 없습니다. 시간복잡도 또한 O(n) 으로 동일합니다.

👉🏻 Python 으로 구현한 코드

# arr를 exp(자릿수)를 기준으로 계수 정렬을 수행하는 함수
def countingSort(arr, exp1):
	n = len(arr);
	result = [0] * (n);
	count = [0] * (10);

	# arr의 각 요소를 자릿수로 나눠, 해당 자릿수에 해당하는 count배열 인덱스에 횟수를 누적한다.
	for i in range(0, n):
		index = arr[i] // exp1;
		count[int((index) % 10)] += 1;

	# count 배열을 각 숫자의 위치가 나타나도록 수정한다.
	for i in range(1,10):
		count[i] += count[i-1];

	# arr 요소를 자릿수에 따라 result에 재배열한다.
	i = n-1
	while i>=0:
		index = arr[i] // exp1;
		result[count[int((index) % 10)] - 1] = arr[i];
		count[int((index) % 10)] -= 1;
		i -= 1;

	# result 배열을 복사해 정렬된 숫자를 넣어준다.
	i = 0
	for i in range(0,len(arr)):
		arr[i] = result[i];

# 기수 정렬을 하는 함수
def radixSort(arr):
	# 배열에서 최댓값을 찾아, 그 값의 자릿수를 기준으로 한다.
	maxNum = max(arr);

    # 자릿수
	exp = 1;
    # 자릿수를 증가시키면서 모든 자릿수에 대해 계수정렬을 반복하여 수행한다.
	while maxNum // exp > 0:
		countingSort(arr, exp);
        # exp는 현재 자릿수 i를 기준으로 10^i값을 가진다.
		exp *= 10;

👉🏻 JavaScript 로 구현한 코드

// 계수 정렬
function countSort(arr, n, exp) {
  let result = new Array(n);
  let count = new Array(10).fill(0);
 
  // count에 횟수를 저장한다.
  for (i = 0; i < n; i++) {
  	let x = Math.floor(arr[i] / exp) % 10;
            count[x]++;
  };
 
  // 현재 자릿수에서의 실제 위치를 나타내도록 count를 수정한다.
  for (i = 1; i < 10; i++) {
    count[i] += count[i - 1];
 
    // result 배열에 넣어준다.
    for (i = n - 1; i >= 0; i--) {
      output[count[x] - 1] = arr[i];
      count[x]--;
    };
 
    // 결과 배열을 복사해 현재 자릿수에 따라 정렬된 숫자를 포함하게 한다.
    for (i = 0; i < n; i++) arr[i] = output[i];
};

// 지수정렬을 수행하는 함수
function radixsort(arr, n) {
  // 최댓값을 찾아 자릿수를 파악한다.
  let max = Math.max(...arr)
 
  // 각 자릿수에 대한 계수정렬을 수행한다. exp는 현재 자릿수 번호로 10^i를 나타낸다.
  for (let exp = 1; Math.floor(max / exp) > 0; exp *= 10) countSort(arr, n, exp);
};

👉🏻 MSD 방식으로 구현한 JavaScript 코드

// n에서 인덱스에 있는 숫자를 가져오는 함수
function digit(n, i) {
  return parseInt(n / Math.pow(10, i - 1) % 10;
};

// 재귀적으로 MSD Radix Sort : 현재 자릿수(exp)를 기준으로 정렬하는 함수
// lo는 정렬이 시작되어야 하는 시작 인덱스이고, hi는 정렬이 끝나야 하는 끝 인덱스를 말한다.
function MSD_Sort(arr, lo, hi, exp) {
  // base case
  if (hi <= lo) return arr;
  
  let count = Array(10 + 2).fill(0);
  // 문자열을 교환하기 위한 임시 Map 생성
  let temp = mew Map();
  
  // 각 정수에서 가장 중요한 문자의 발생 횟수를 저장
  for (let i = lo; i <= hi; i++) {
    let c = digit(arr[i], exp);
    count[c]++;
  };
  
  // count에 각 숫자의 위치가 나타나도록 수정
  for(let i = 0; i < 10 + 1; j++) count[r + 1] += count[r];
  
  // temp Map 을 구성
  for( let i = lo; i <= hi; i++) {
    let c = digit(arr[i], exp);
    if(temp.has(count[c]) temp.set(count[c]++, arr[i]);
    else temp.set(count[c]++, arr[i]);
  };
  
  // temp를 복사해 arr이 부분적으로 정렬된 정수를 포함하게 한다.
  for(let i = lo; i <= hi; i++) {
    if(temp.has(i - lo) arr[i] = temp.get(i - lo);
    
    // 각 부분적으로 정렬된 arr에 대해 다음 자릿수로 정렬하기 위해 재귀적으로 호출
    for(let j = 0; j < 10; j++) {
      arr = MSD_Sort(arr, lo + count[j], lo + count[r + 1] - 1, exp - 1);
    }
    return arr;
  };
  
  // 가장 큰 숫자의 자릿수를 계산해 MSD_Sort함수를 호출해 정렬한다.
  function radixSort(arr, n) {
    let max = Math.max(...arr);
    let exp = parseInt(Math.fllor(Math.log10(Math.abs(max)))) + 1;
    
    return MSD_Sort(arr, 0, n - 1, exp);
  }

☀️ Time and Space Complexity Analysis ( 시·공간 복잡도 )

시간복잡도

  • 정렬을 위한 비교연산을 하지 않는 특징을 가져, 정렬 알고리즘의 이론상 성능의 한계인 O(NlogN)을 넘는 유일한 알고리즘입니다. 정확하게는 O(k * n)의 시간복잡도를 가집니다. (k는 가장 긴 자릿수, n은 요소의 수를 뜻합니다.) 따라서, O(n) 의 시간복잡도를 가집니다.

  • 실제 구현에서 기수정렬은 특히 키에 숫자가 많은 경우, 대규모 데이터 세트의 경우 퀵 또는 병합 정렬보다 빠른 경우가 많습니다. 그러나 시간복잡도는 자릿수에 따라 선형적으로 증가하므로 작은 데이터 셋에는 효율적이지 않습니다.

공간복잡도

  • 일반적인 LSD 방식의 구현에서는 O(n + k)의 공간복잡도를 가집니다(n은 배열의 요소의 수이고, k는 최하위 숫자 값의 범위입니다). 각 숫자 값(0 ~ 9)에 대한 버킷을 생성하고 각 숫자가 정렬된 후 요소를 원 배열에 다시 복사해야하기 때문에 발생합니다. 따라서 'k'가 상수인 경우 O(n) 의 공간복잡도를 가집니다.

  • MSD 방식의 구현은 재귀를 사용하므로 최대 유효 숫자의 가능한 각 값에 대한 버킷을 저장하기 위해 추가로 공간이 더 필요합니다. 최악의 경우 공간복잡도는 O(n^2) 가 됩니다.

🌿 In-Place Radix Sort

추가 공간 사용량을 줄이기 위해 요소를 교체하여 올바른 위치로 이동하는 등의 기술을 사용해 입력 배열을 제자리에서 수정하도록 정렬 내부를 변형할 수 있습니다. 내부 기수 정렬 알고리즘은 버킷이나 저장소에 추가 메모리를 사용하지 않으므로 O(1)의 공간복잡도를 가집니다.
다만, 입력 값의 범위나 LSD, MSD 방식 등 조건에 따라 공간복잡도는 달라질 수 있습니다.

🪴 Finish

  • 작동 방식에 대해서는 그림으로 그리면서 쉽게 이해했는데, 이를 코드로 구현하는 부분이 어려웠다. 구글링을 통해 코드를 얻었고, 이에 대해 주석을 쓰며 이해해봤지만 혼자 구현하라고 하면 어려울 것 같다. 또 MSD 방식 구현에 대해서는 이해가 많이 부족하다. 더 많은 공부가 필요하다고 느꼈다.
  • JS코드로 LSD방식의 코드를 구현해 중간에 인용한 동영상처럼 시각적으로 구현해봐야겠다.

👀 Reference

profile
NewHa
백 번을 보면 한 가지는 안다 👀

0개의 댓글