[ ᴀʟɢᴏʀɪᴛʜᴍ ] Tree Data Structure ( 트리 )

NewHa·2023년 9월 21일

ᴀʟɢᴏʀɪᴛʜᴍ

목록 보기

12/14

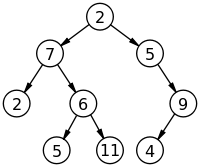
🌱 Tree ( 트리 )

👉🏻 트리 (tree, 構造, 나무구조) : 탐색 및 검색하기 쉬운 방식으로 노드(node)으로 불리는 데이터 요소 간 계층적 관계를 표현하고 구성하는 데이터 구조입니다. 노드들 사이에 부모-자식 관계가 있어서 계층적 구조를 나타내는 데 적합하며, 이러한 모습이 나무가 가지를 치고 나가는 것 같은 구조와 비슷해 트리 구조라고 부릅니다. 데이터를 보다 효과적으로 사용할 수 있도록 구성하고 저장하는 특수항 방법입니다.

그래프의 한 종류로, 사이클이나 회로가 없는 특수한 연결 비순환 그래프이면서 트리를 구성할 때 데이터가 순차적으로 저장되지 않는 비선형 데이터 구조입니다. 또한 노드간에 상-하(부모-자식)로 방향을 가지는 방향성 그래프입니다. 루트노드를 제외하고 모든 노드는 특정 상위 노드를 가지고, 여러 하위 노드를 가지거나 가지지 않을 수 있습니다.각 노드에는 하위 항목에 대한 값과 참조값을 포함합니다.
트리는 시작 지점인 루트가 하나의 노드여야 합니다. 그 아래로 부모-자식관계에 따라 간선은 화살표로 표현하는데, 자식인 노드만 가리킬 수 있습니다. 노드가 자신보다 낮지 않은 부모나 형제 노드를 가리키면 그 구조는 트리라고 할 수 없고 그래프에 해당합니다.
배열이나 연결 리스트 등 다양한 방법으로 표현할 수 있으나, 일반적으로 노드를 원으로 노드들간의 연결은 선으로 하여 그래픽으로 표현합니다. 이전의 자료구조들이 데이터를 저장하고 꺼내어 쓰는데 집중되는 자료구조였다면 트리는 표현을 위해 그러한 기능을 제공합니다.
노드 내에는 꼭 숫자가 들어있을 필요는 없고, 어떠한 데이터든지 저장할 수 있습니다.
🌿 vs 다른 데이터 구조와의 차이점
- 그래프와 트리의 차이점 (👉🏻 graph 글을 참고해주세요.)
- 힙과 트리의 차이점
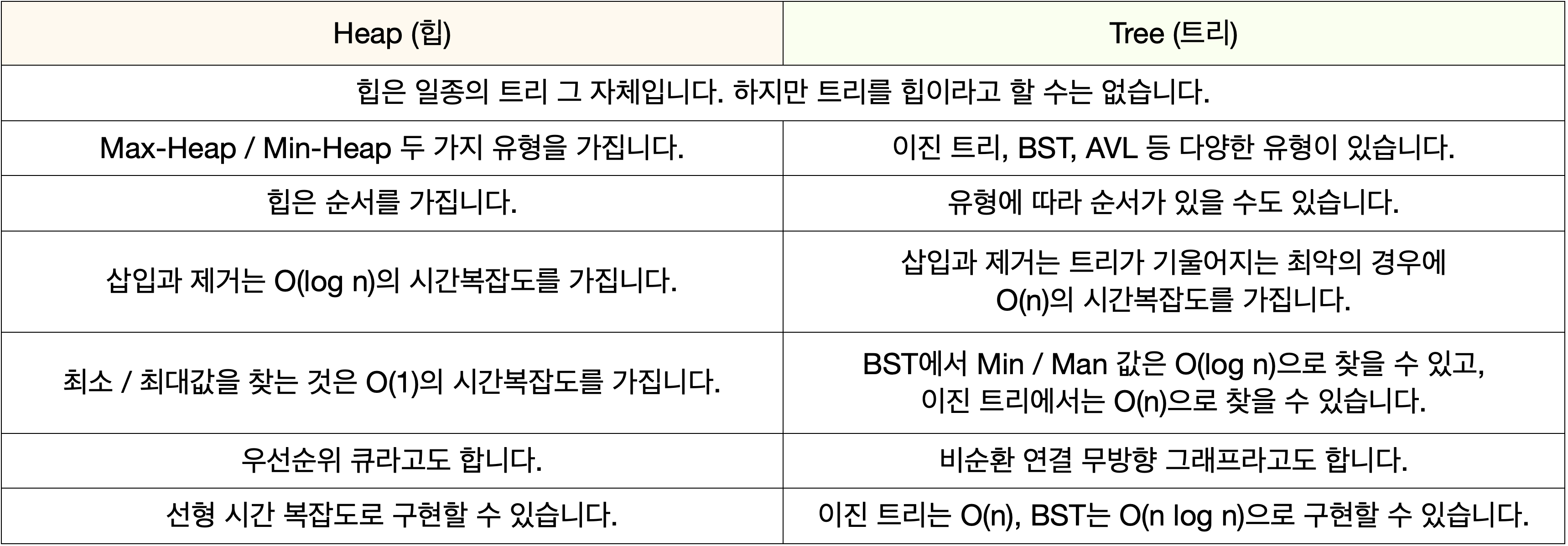
- 연결리스트와의 차이점

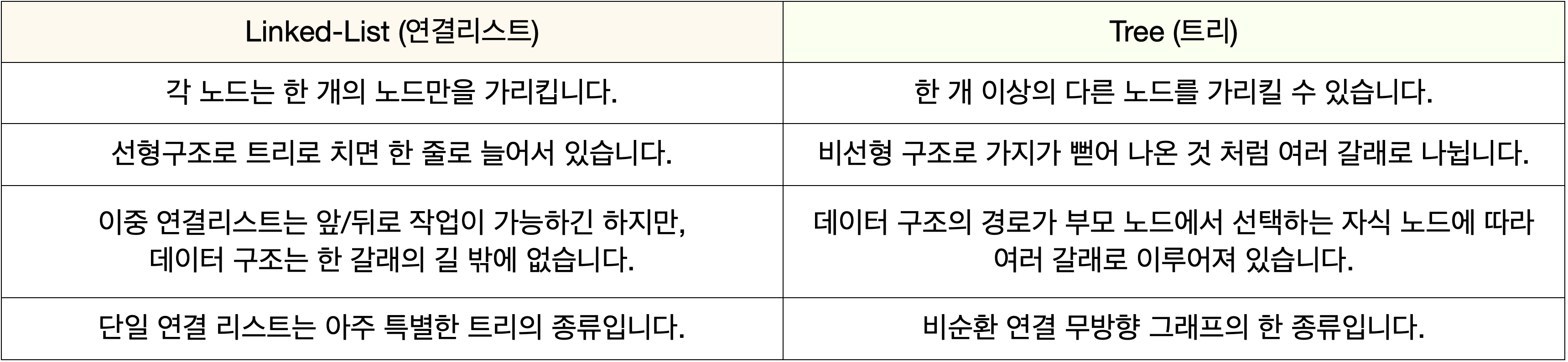
☀️ Characteristic of Tree ( 특징 )

🪴 속 성

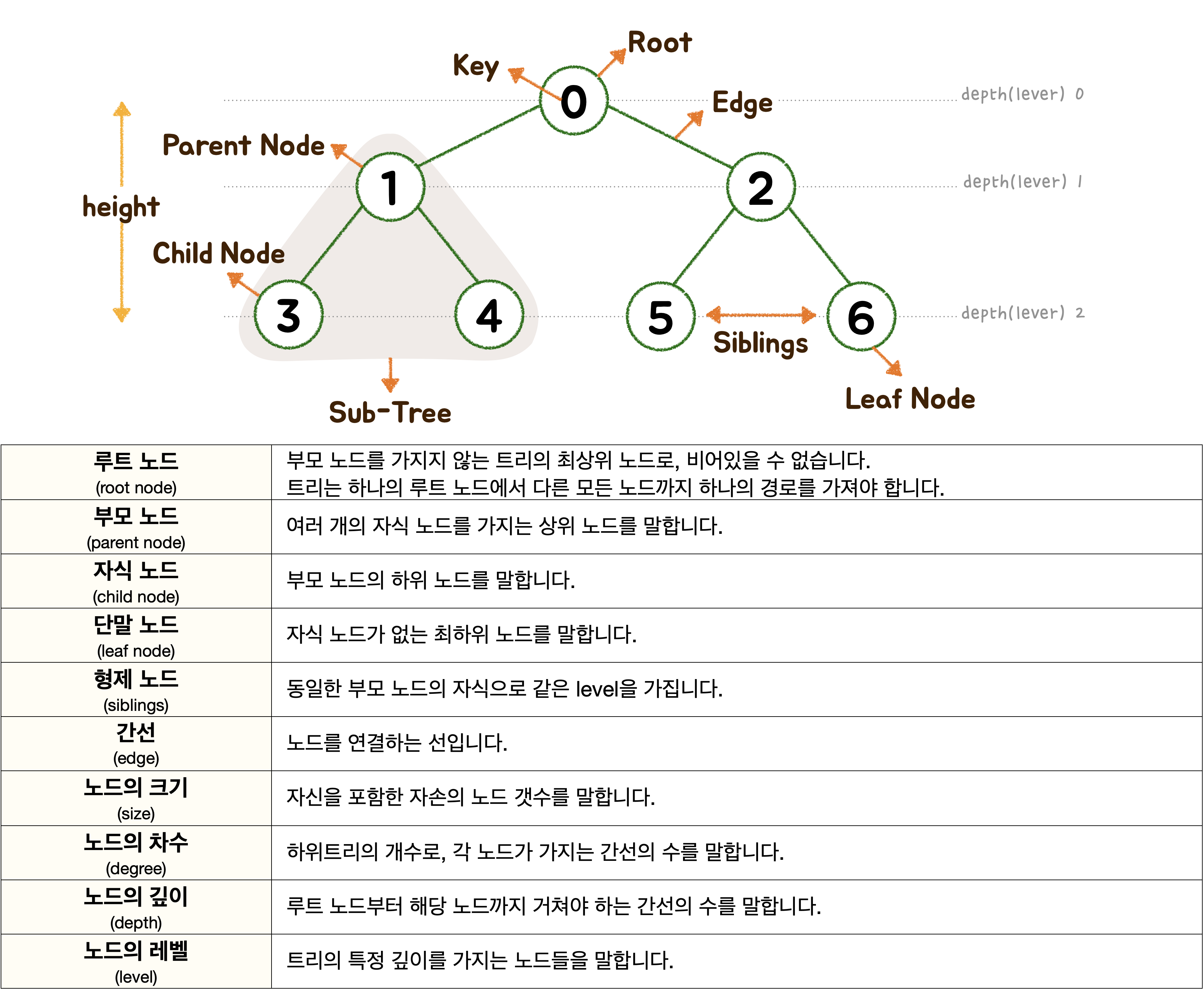
🙆🏻‍♀️ 장 점

데이터가 삽입될 때 자동으로 정렬되므로 최소, 최대, 기타의 값을 검색하는 데 효율적입니다. 매우 큰 데이터 셋에서도 매우 빠르게 작동하여 평균적으로 O(log n)시간안에 검색합니다.
데이터의 계층적 표현을 제공하여, 많은 양의 정보를 쉽게 구성하고 탐색가능케 합니다. 파일시스템, 조직구조, 분류 같은 다양한 유형의 관계를 자연스러운 계층적 조직으로 나타내는 데 유용합니다. 부모-자식 관계를 자연스럽게 표현할 수 있으므로 쉽게 이해하고 시각화할 수 있습니다.
추가되거나 제거되는 노드 수에 따라 동적으로 데이터가 증감합니다. 실시간 시스템 같이 데이터가 자주 변하는 애플리케이션이나, 시간이 지남에 따라 데이터 크기가 변경될 수 있는 애플리케이션에 유용합니다.
노드 간 엄격한 계층구조와 관계를 적용하므로 나머지 구조에 영향을 주지 않고 노드를 추가하거나 제거, 수정하기가 쉬워 유지관리가 용이합니다.
효율적인 삽입, 삭제 시간을 가져 데이터를 자주 추가하거나 제거할 일 많은 애플리케이션에 적합합니다.

🙅🏻‍♀️ 단 점

데이터의 크기가 매우 큰 경우, 상당한 메모리 공간을 요하므로 리소스에 제한이 있는 애플리케이션에서 문제가 될 수 있습니다.
트리의 구조가 불균형하면 검색 시간이 고르지 않을 수 있습니다. 이는 속도가 중요한 애플리케이션에서 문제가 될 수 있습니다.
데이터의 구조가 복잡하다면 올바르게 이해하고 트리 구조로 구현하는 것이 어려울 수 있습니다. 구현하더라도 조작이 복잡할 수 있습니다.
크기나 구조적으로 유연하지만 다른 데이터 구조만큼 유연성을 가지진 않습니다. 데이터 크기가 자주 변경되는 애플리케이션에서는 문제가 될 수 있습니다.
정렬과 그룹화 같은 다른 작업에는 비효율적일 수 있습니다.

🪴 활 용

운영체제에서 파일시스템은 트리형식을 가집니다. 폴더들은 모두 서열을 가지는 노드이고 파일은 leaf에 해당합니다.
HTML/XML 문서를 구문 분석하고 처리하는 데 사용됩니다. 그 자체로 트리 구조를 가지고 여러 요소들을 노드로, 그 요소 안에 자식에 해당하는 다른 요소가 중첩되어 있습니다. HTML문서를 브라우저에 요청하고 응답을 받아 브라우저가 내용을 읽어서 만드는 문서 객체 모델, 즉 DOM도 트리구조를 가집니다.
DNS에서 트리 구조를 사용하여 데이터를 검색하는 효율적인 방법을 제공하고, log 시간을 소요해 선형 구조보다 빠르게 결과를 보여줍니다.
인공지능에서 의사 결정 트리로 항상 사용됩니다. 인공지능에게 일련의 기준에 따라 결정을 내리게 하는 데 사용됩니다.
프로그래밍 언어의 구문은 종종 구문 분석 트리라는 트리구조를 사용해 정의됩니다. 컴파일러가 트리 구조로 코드 구조를 이해하고 기계어 코드 생성에 사용합니다.
데이터 베이스는 트리 구조를 사용해 데이터를 인덱싱합니다.
여러 게임에서 사용됩니다. 예컨대, 틱택토 게임을 만든다고 할 때 게임의 논리 구조를 트리로 나눠서 모든 경우의 수를 다루어 가장 최선의 다음 수를 두도록 할 수 있습니다.
🌿 예시
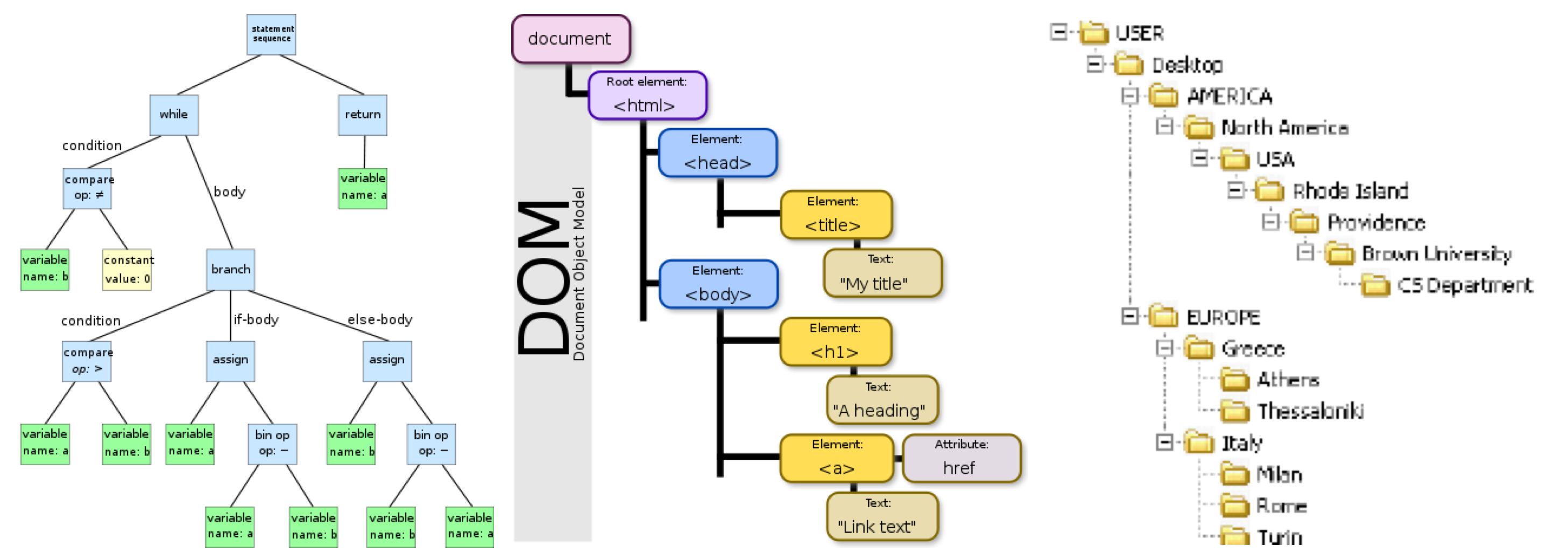
- 👆🏻 구문 분석 트리 (왼) / DOM Tree (중) / Directory Tree (오) (클릭시 출처로 이동)

☀️ Type of Tree ( 유형 )

다양한 트리의 유형이 존재합니다. 대표적으로 많이 쓰이고 언급되는 트리는 이진 트리와 이진 검색 트리입니다.

🪴 Generic Tree(일반 트리, N-ary Tree)

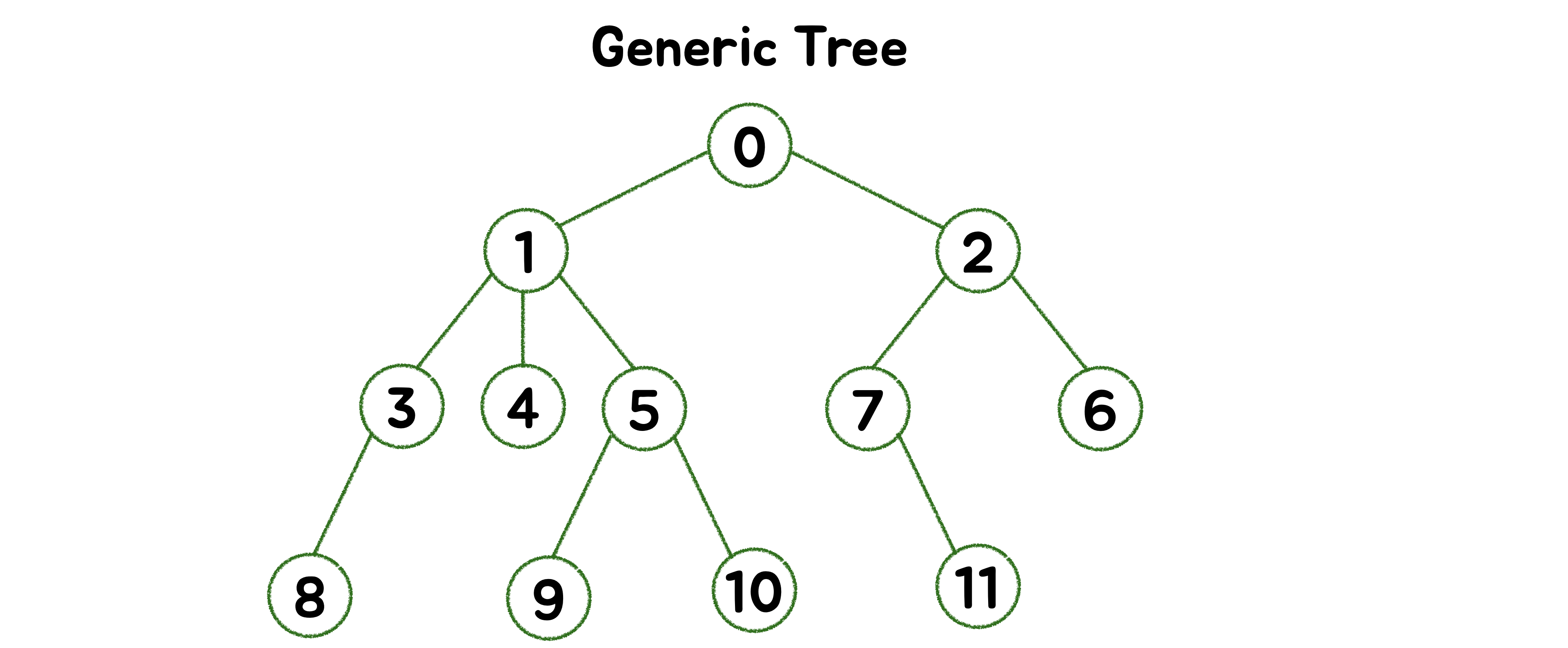
🪴 Binary Tree (이진 트리)

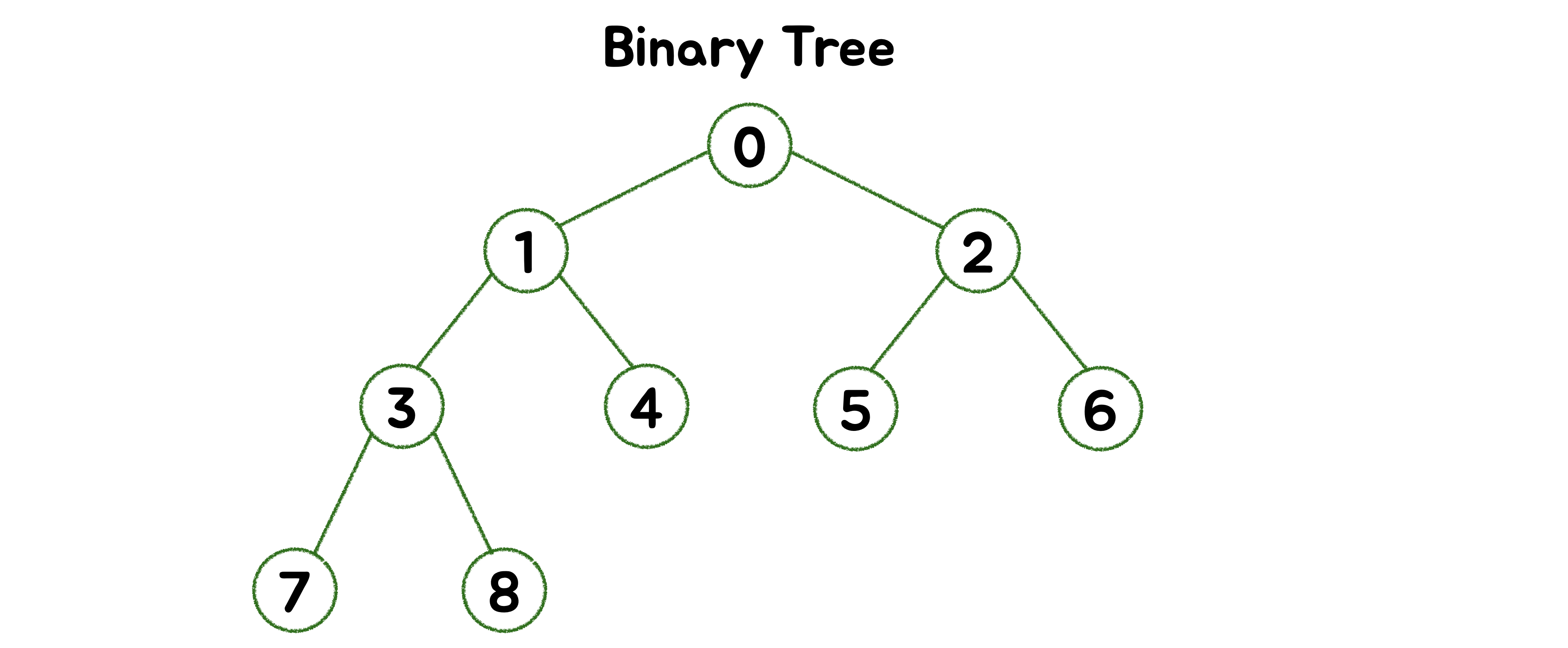
각 노드가 최대 두 개의 자식을 가져야 한다는 특별한 조건을 가지는 트리로, 루트 노드를 기준으로 두 개의 서브 트리로 나누어지고, 나누어진 서브트리도 모두 이진 트리여야 합니다. 즉, 조건 자체가 재귀적으로 이진트리를 구성하며 재귀적이므로 순회가 쉽다는 장점을 가집니다.

이진 트리는 포화 이진 트리, 완전 이진 트리, 균형 이진 트리 등 다양한 유형으로 또 나누어지나 이는 이진 트리 게시물에서 소개하겠습니다.

🪴 Binary Search Tree (이진 검색 트리, BST)

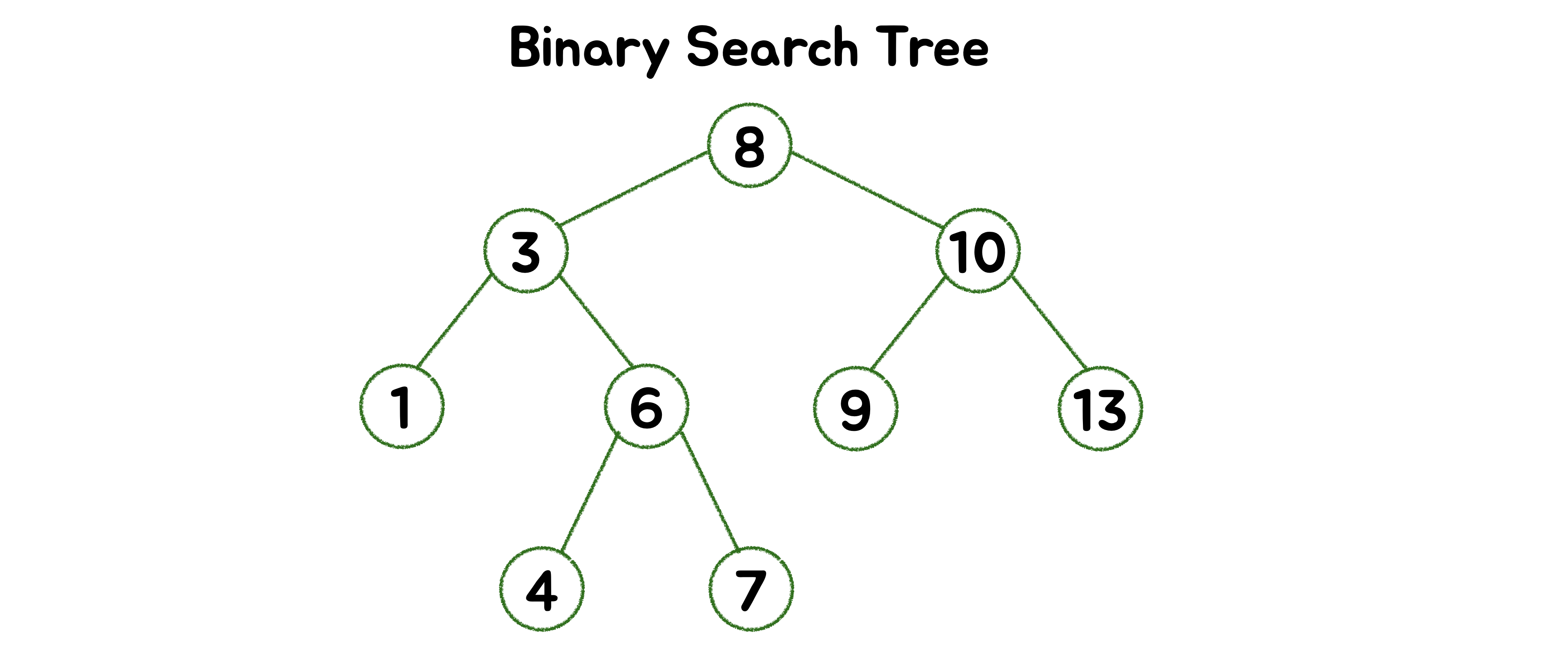
데이터를 특정한 방식으로 저장하는 이진 트리로 데이터가 순서에 따라 저장됩니다. 이진 트리와 같이 노드 당 최대 두 개의 자식을 가지며, 데이터를 비교해서 순서를 매기는 방법에 따라 비교 정렬 합니다. 부모 노드 왼쪽에 있는 모든 노드는 언제나 부모 노드보다 작고, 부모 노드보다 오른쪽에 있는 모든 노드는 언제나 부모 노드보다 큽니다. 검색에 특화되어 있습니다.

자세한 사항은 이진 트리 게시물에서 소개합니다.

🪴 Ternary Tree (삼항 트리)

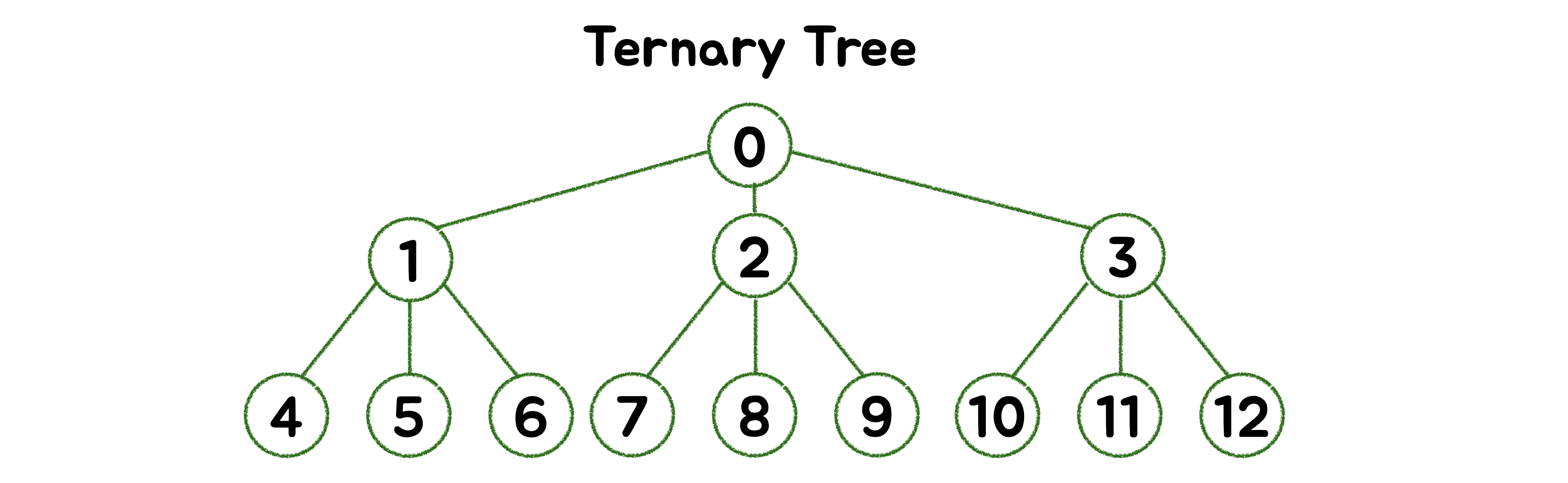
각 노드가 일반적으로 왼쪽, 중간, 오른쪽으로 구분되는 최대 3개의 하위 노드를 갖는 트리 구조 입니다. 하위 노드가 이진 검색 트리로 정렬되는 삼항 검색 트리가 더 많이 쓰입니다.

🪴 AVL Tree (Adelson-Velskii 및 Landis)

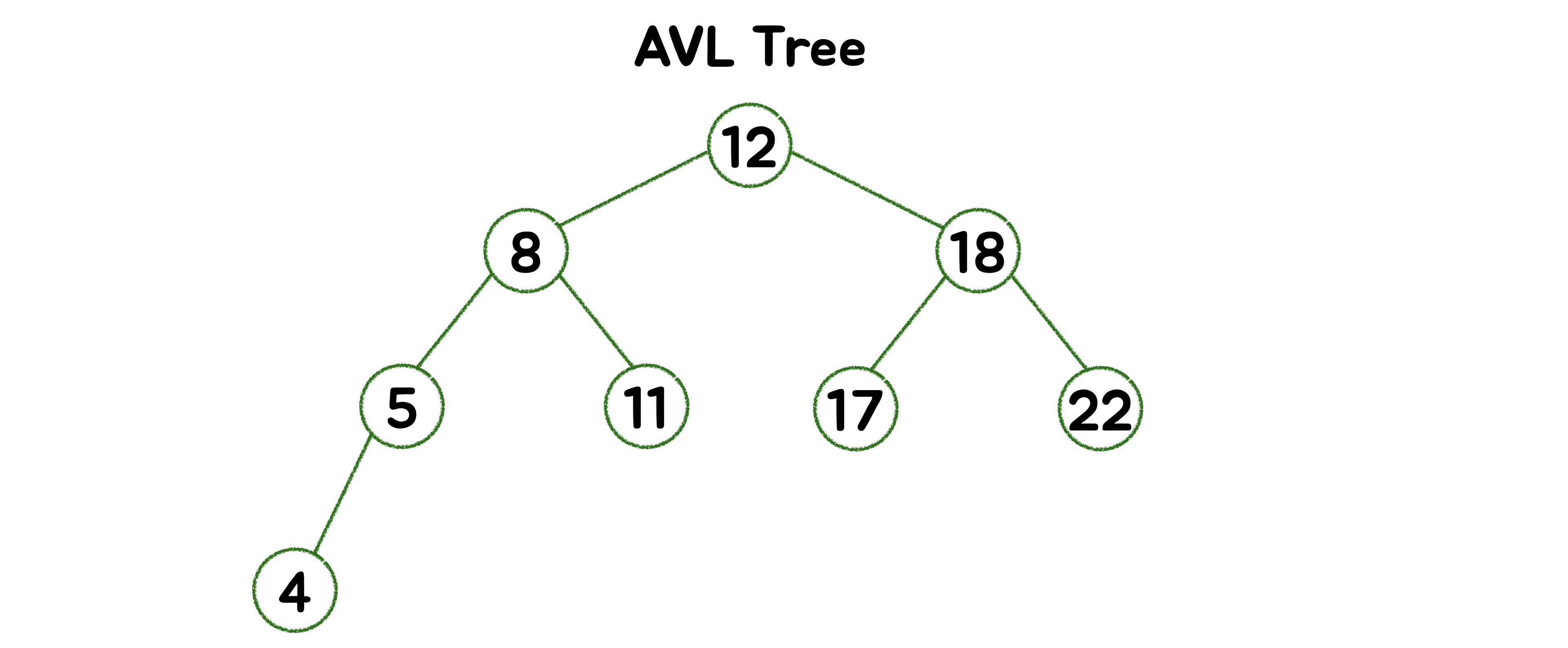
균형트리 중에 하나로, 모든 노드의 왼쪽 및 오른쪽 하위 트리 높이 차이가 1보다 클 수 없는 자체 균형형 이진 검색 트리(BST)입니다. 이러한 높이 차이를 노드의 균형 요소라고 합니다.
더 엄격한 균형으로 검색 속도가 빠르지만, 이로 인해 복잡한 삽입 및 제거 작업을 수행합니다.

🪴 Red-Black Tree

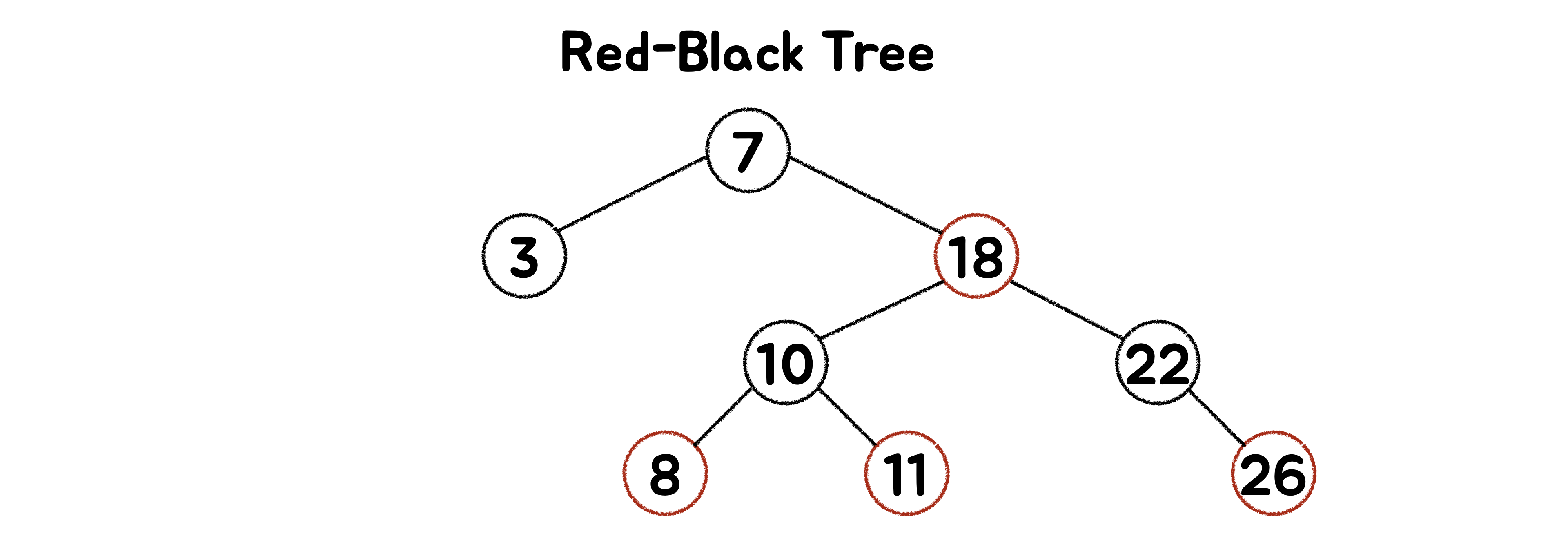
균형트리 중 하나로, 각 노드에 추가 비트가 있고, 해당 비트가 빨간색 또는 검은색 색상으로 해석되는 일종의 자체 균형 이진 검색 트리(BST)입니다. 이러한 색상은 삽입 및 삭제 중에 트리의 균형이 유지되도록 하는 데 사용됩니다. 트리의 균형이 완벽하지는 않지만 검색시간을 줄이고 O(log n) 시간 정도를 유지하는 데 충분합니다. 즉, VAL보다 검색 속도는 느리지만 더 빠른 삽입 및 제거 작업을 수행합니다.

이 외에도 B-Tree, B+ Tree, 세그먼트 트리 등 다양한 유형이 존재합니다.

☀️ Implements of Tree ( 구현 )

🎄 트리 만들기

일반 트리는 모든 노드에 많은 자식 노드가 있을 수 있고, 각 노드의 자식 노드 수를 미리 알 수 없습니다. 일일히 자식 노드를 추가하는 방식은 메모리 낭비가 많이 발생합니다. 배열이나 연결 리스트를 사용해 구현할 수도 있지만 각 문제를 가집니다.

연결리스트 : 어떤 자식의 주소에도 무작위로 접근할 수 없고, 비용이 많이 듭니다.
배열 : 임의의 자식 주소에 무작위로 접근할 수는 있지만 고정된 수의 자식 주소만 저장할 수 있습니다.

👉🏻 이를 해결하기 위해 자식 노드에 동적 배열을 할당합니다. 메모리를 절약하고, 이후에 쉽게 이진 트리로 변환할 수 있습니다.

class Node {
  constructor(data) {
    this.data = data;
    this.child = [];
    // 노드의 갯수를 알고 있다면 다음과 같이 쓸 수 있습니다.
    // this.child = Array(n);
  }
}
// 각 노드에서 왼쪽과 오른쪽에 자식을 연결합니다.
// 💈 그리고 첫번째 하위 노드를 제외한 모든 상위 링크를 제거하면 메모리를 절약할 수 있습니다.
class ChildNode {
  constructor(data) {
    this.data = data;
    this.left = this.rigth = null;
  }
}

🌿 트리 순회

트리 데이터 구조는 선형 데이터 구조와 달리, 다양한 방식으로 순회할 수 있습니다.

너비 우선 검색 (BFS)

깊이 우선 검색 (DFS) 👉🏻 선위 순회, 중위 순회, 후위 순회

경계 순회

대각선 횡단 순회

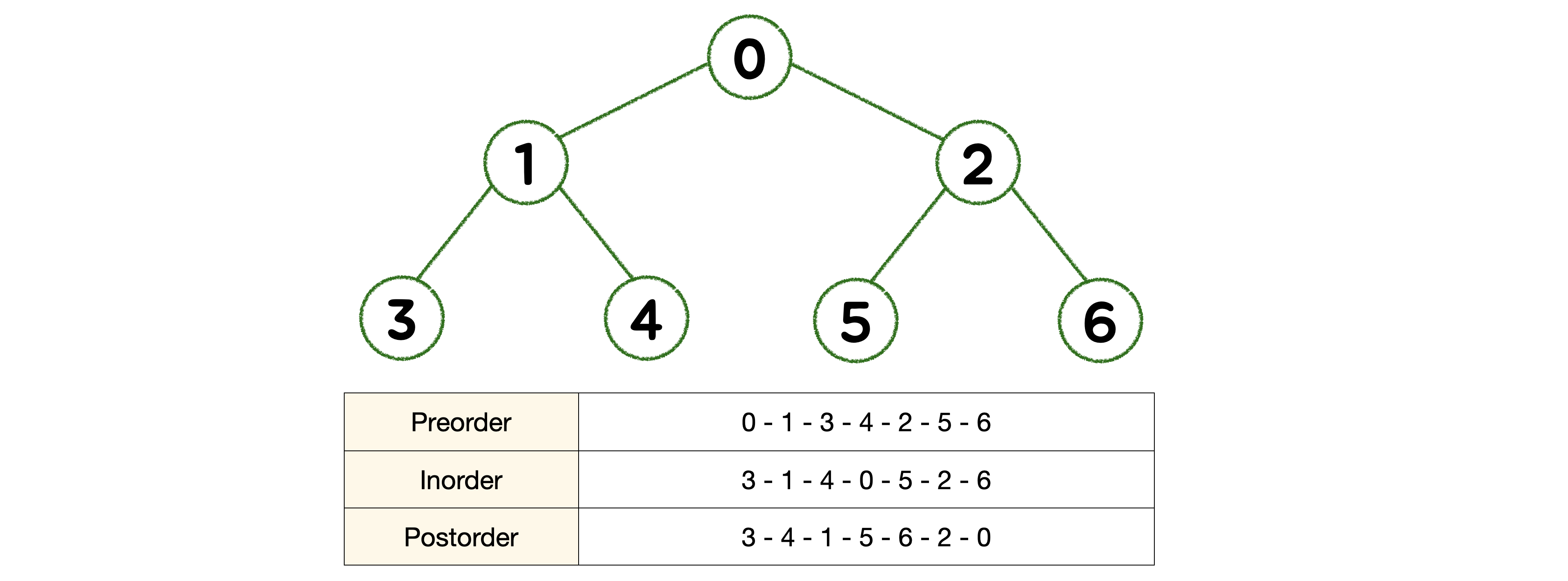
🎄 DFS - Preorder ( 전위 순회 )

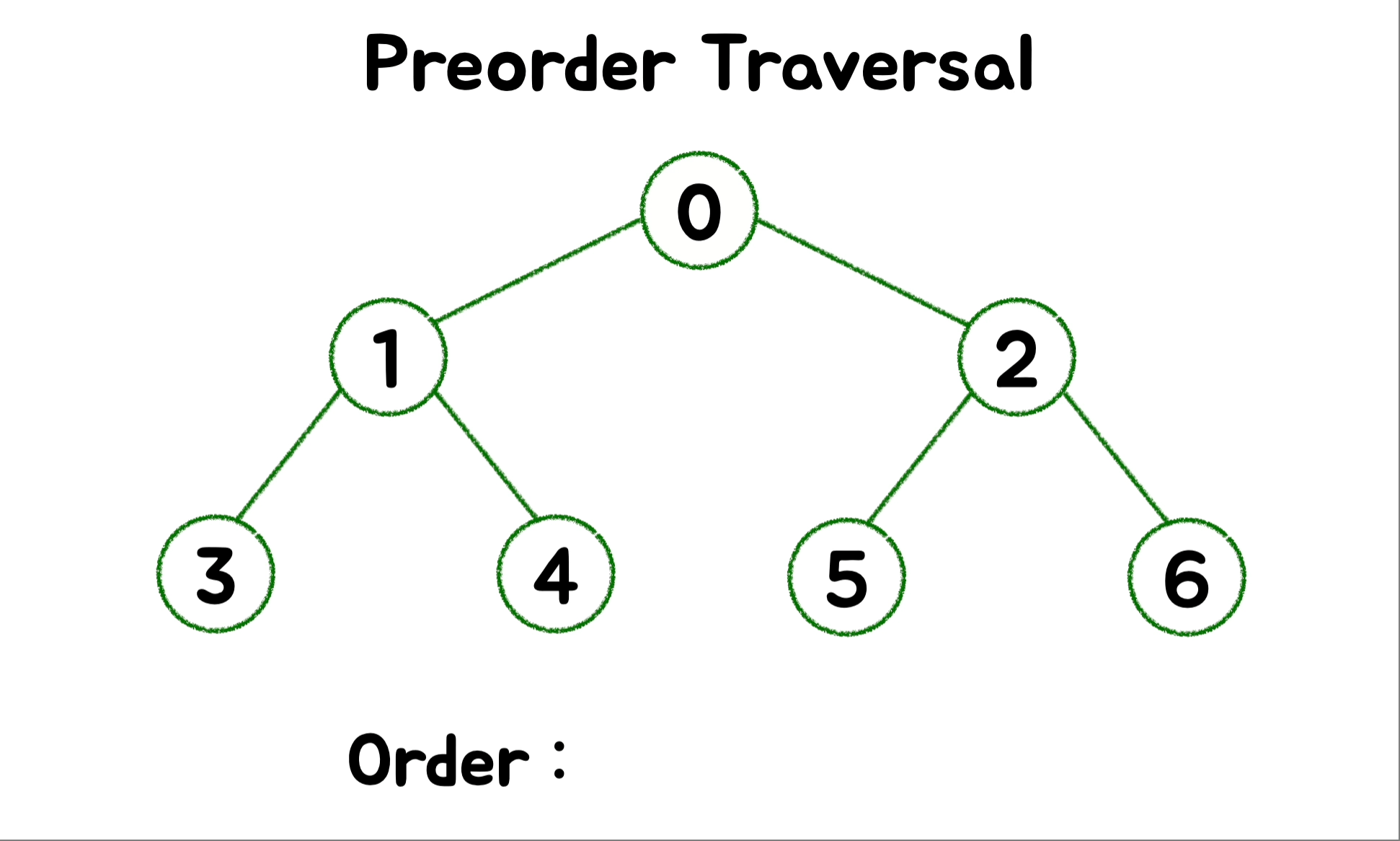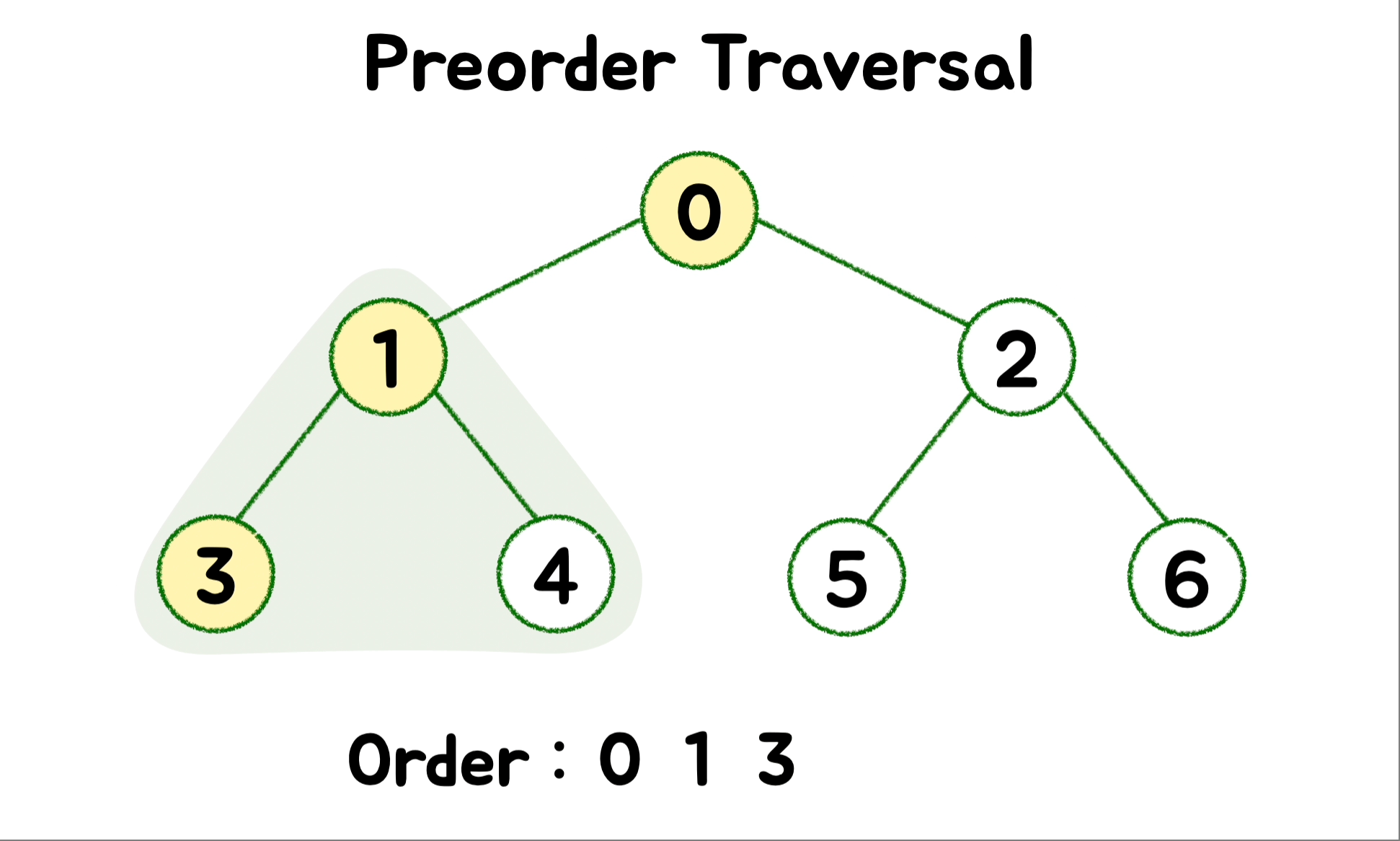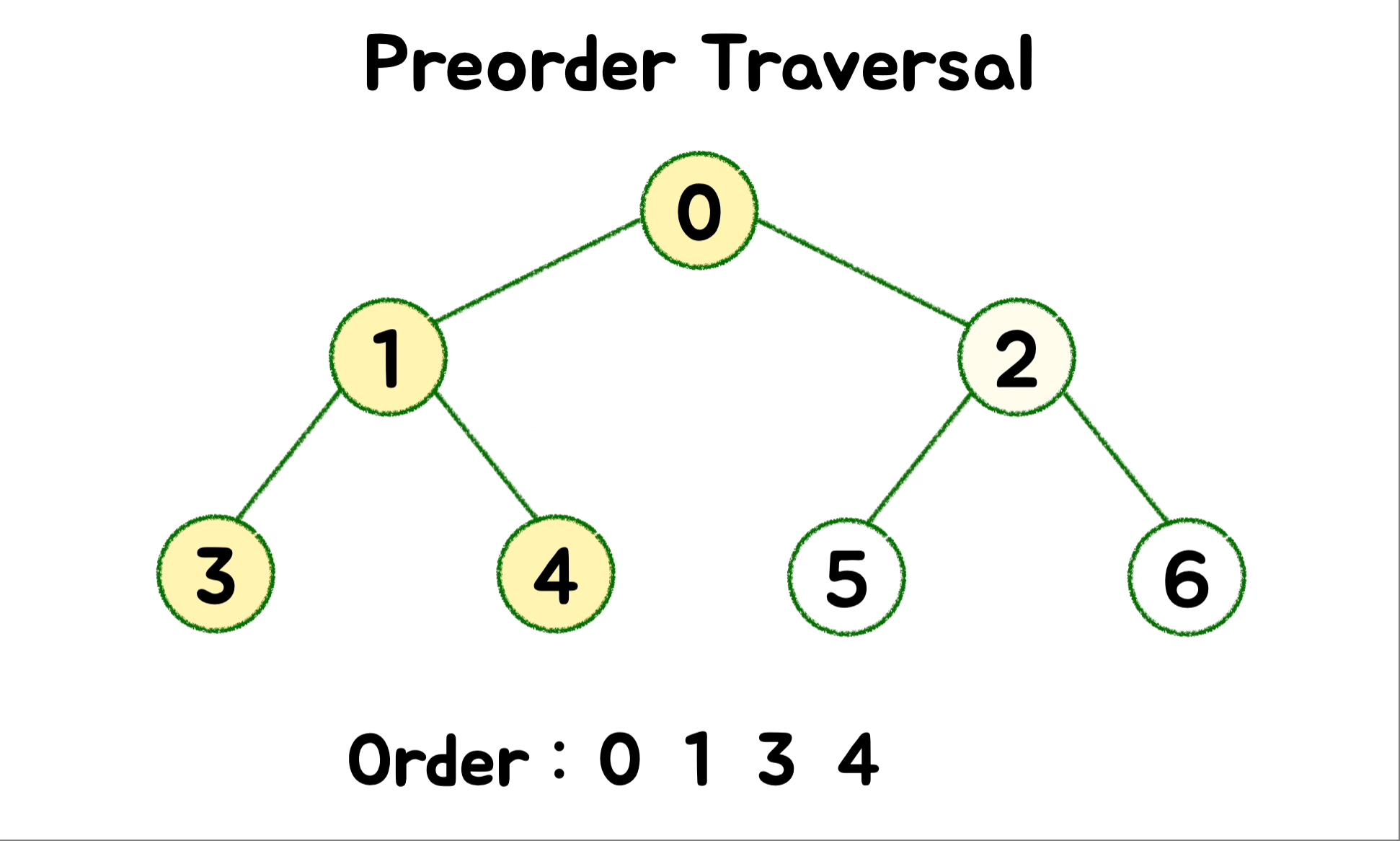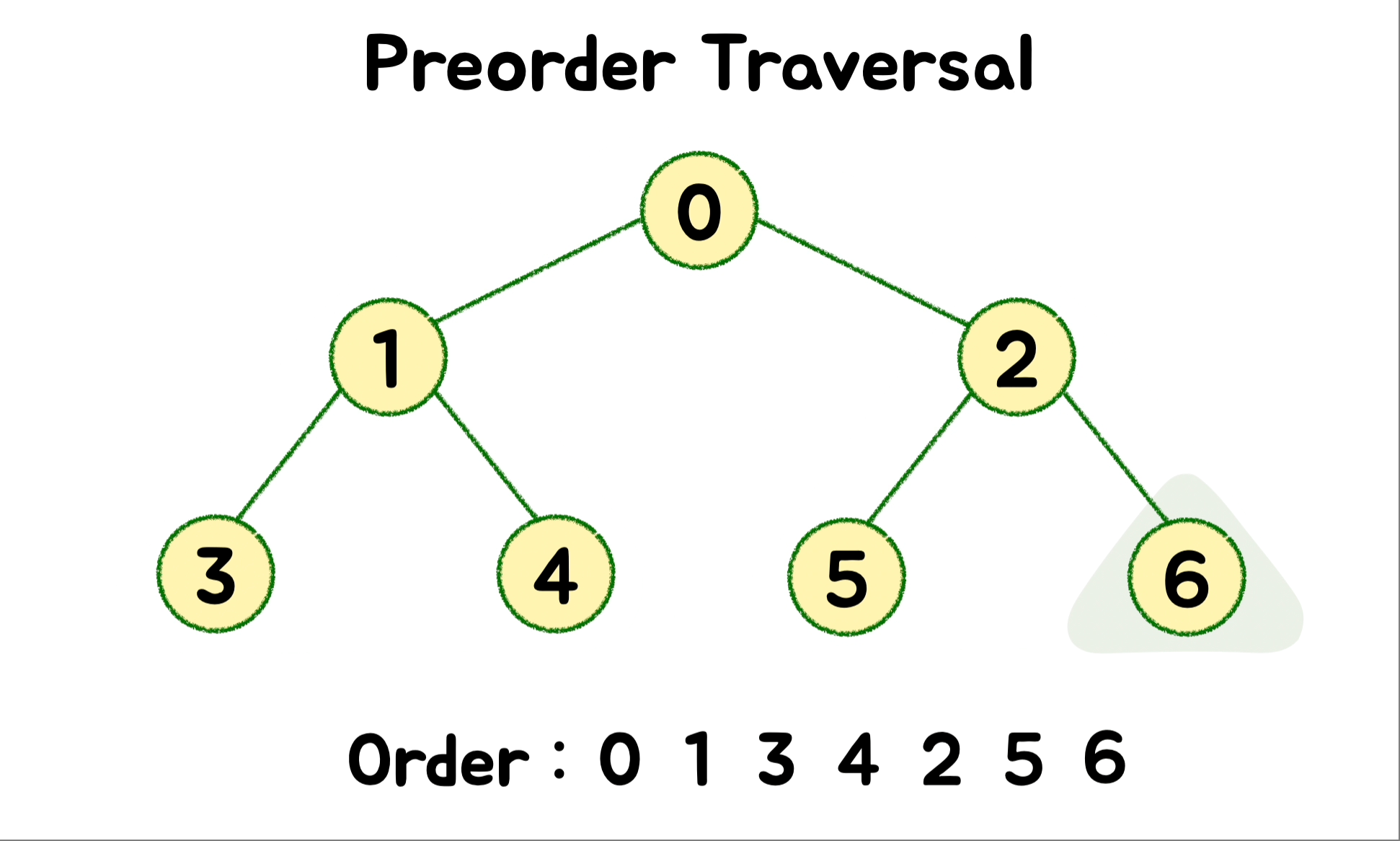
트리의 복사본을 만드는 데 사용합니다. 루트를 먼저 방문하고 왼쪽 하위 트리를 호출해 탐색합니다. 그 다음으로 오른쪽 하위 트리를 호출해 탐색합니다.

let root = null; 

function preorder(node) {
  if(node === null) return;
  
  let total = node.child.length;
  for(let i = 0; i < total - 1; i++) {
    console.log(node.data + '-'); 
    preorder(node.child[i]); // left node
    preorder(node.child[total - 1]); // right node
  }
}

🎄 DFS - Inorder ( 중위 순회 )

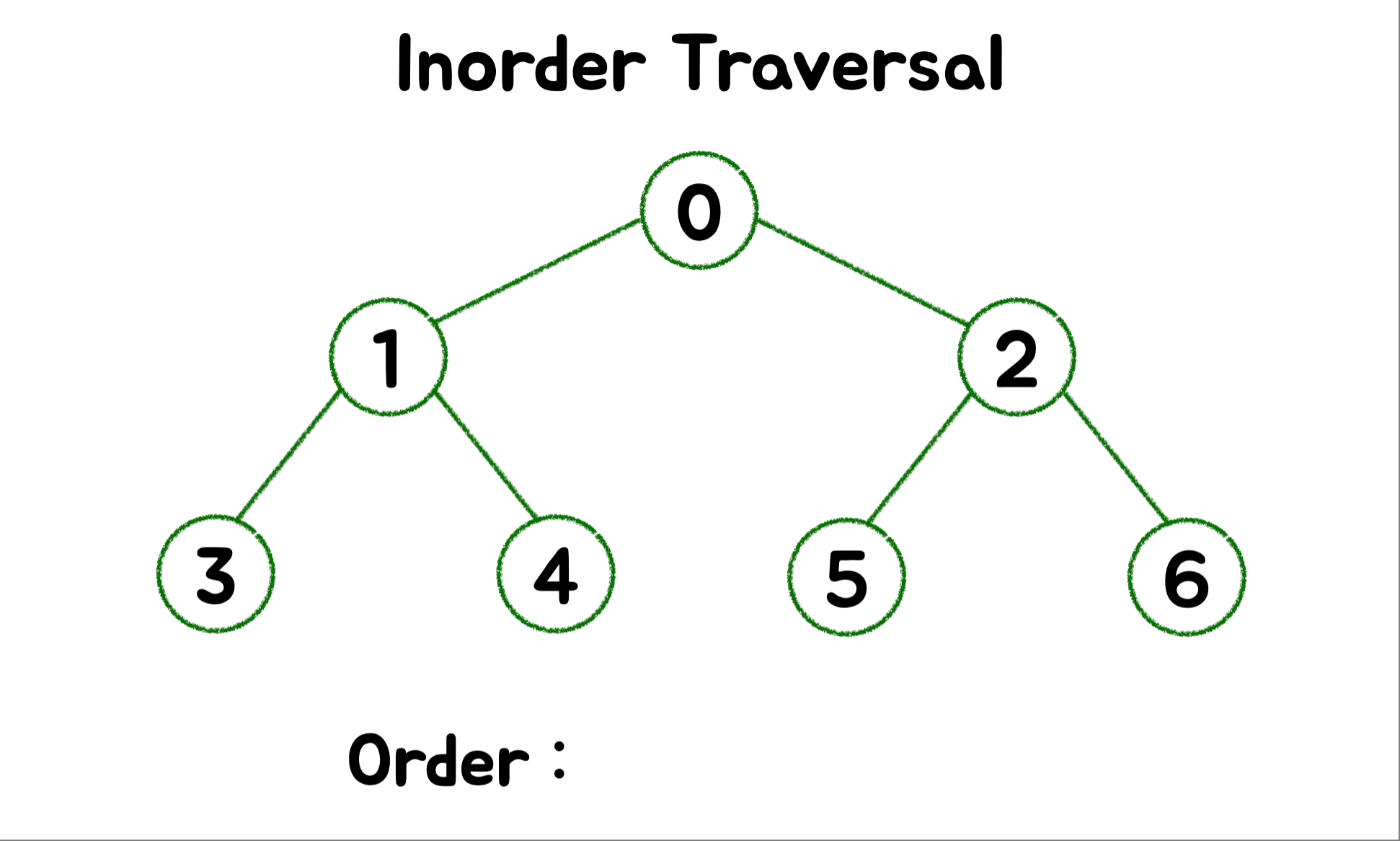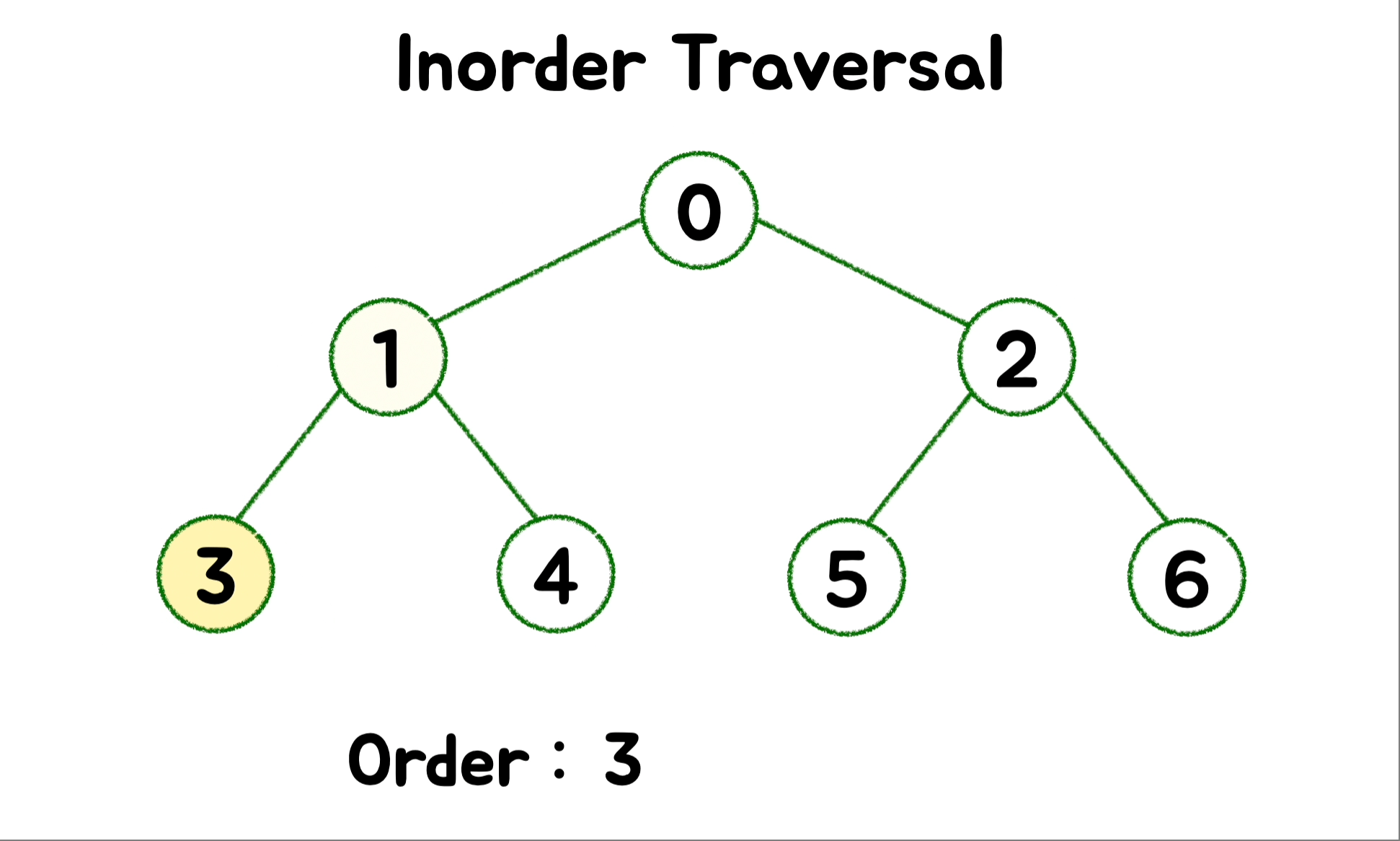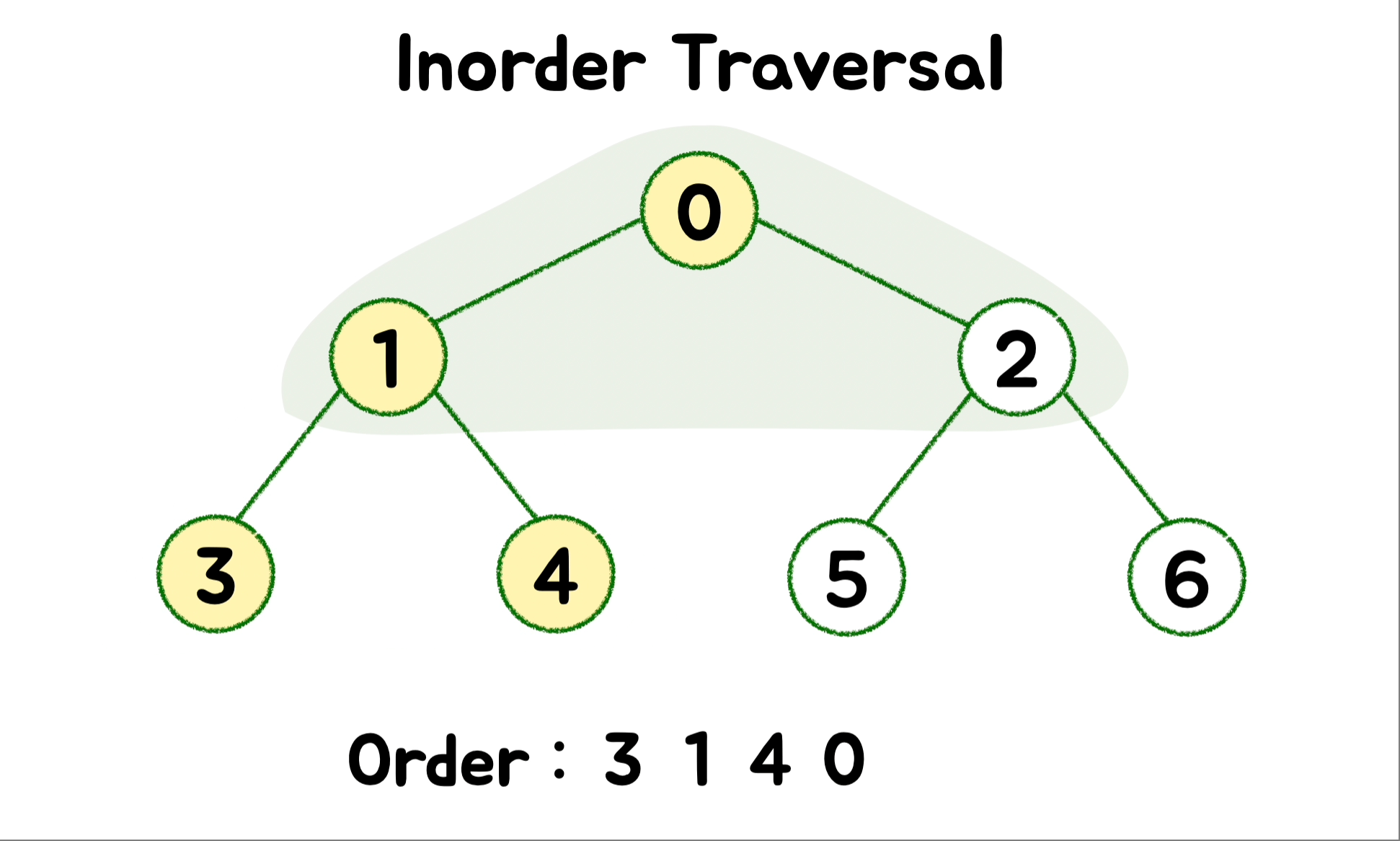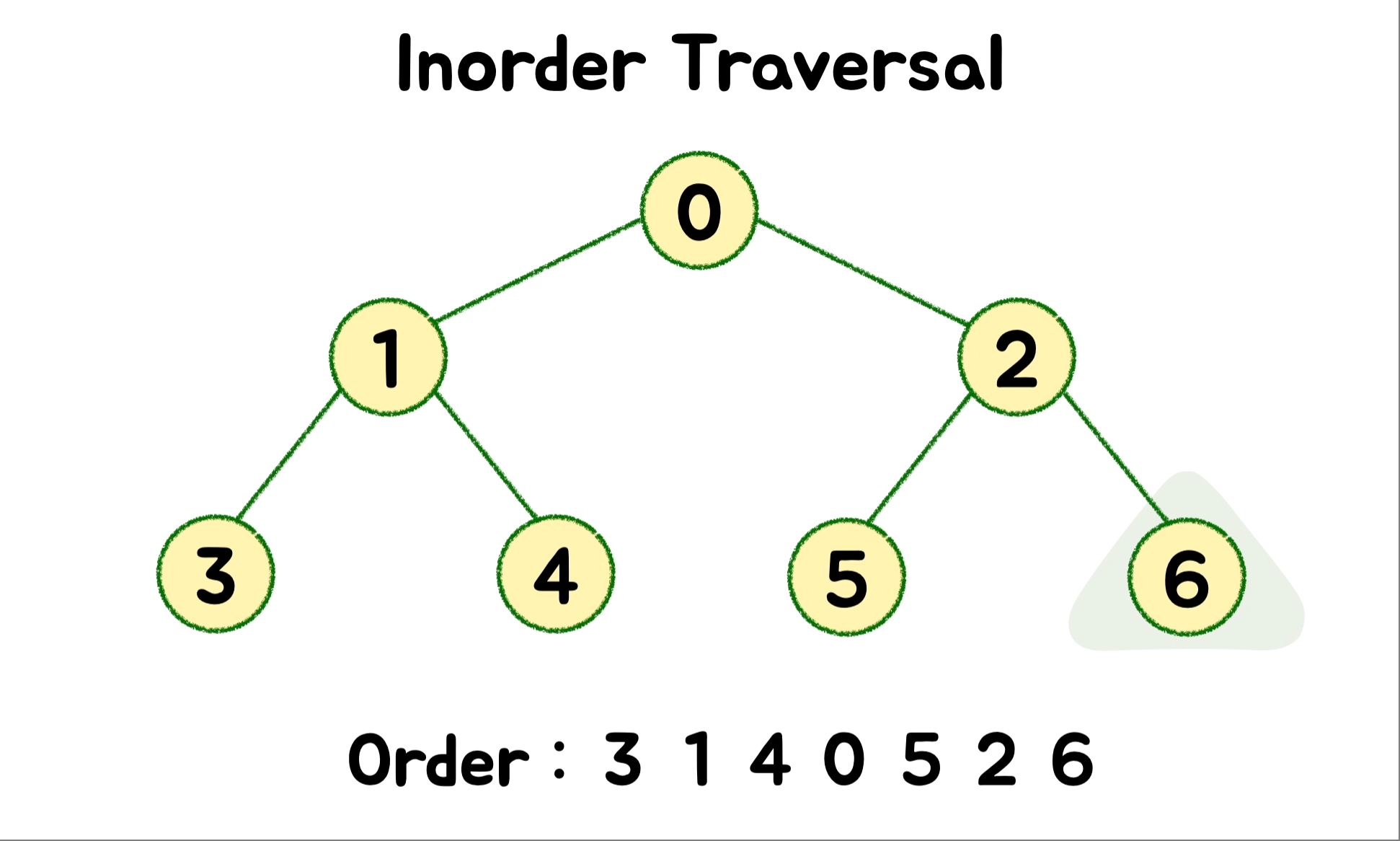
왼쪽 하위 트리를 호출해 탐색하고, 루트를 방문한 다음으로 오른쪽 하위 트리를 호출해 탐색하는 순서로 순회합니다.

let root = null;

function inorder(node) {
  if(node === null) return;
  
  let total = node.child.length;
  for(let i = 0; i < total - 1; i++) {
    inorder(node.child[i]); //left node
    console.log(node.data + '-');
    inorder(node.child[total - 1]); // right node
  }
}

// 💈 재귀 없이 stack을 사용해 중위 순회할 수 있습니다.
function inorder() {
  if(root === null) return;
  const stack = [];
  let cur = root;
  while(cur !== null || stack.length > 0) {
    while(cur !== null) {
      stack.push(cur);
      cur = cur.left;
    }
    cur = stack.pop();
    console.log(cur.data);
    cur = cur.right;
  }
}

🎄 DFS - Postorder ( 후위 순회 )

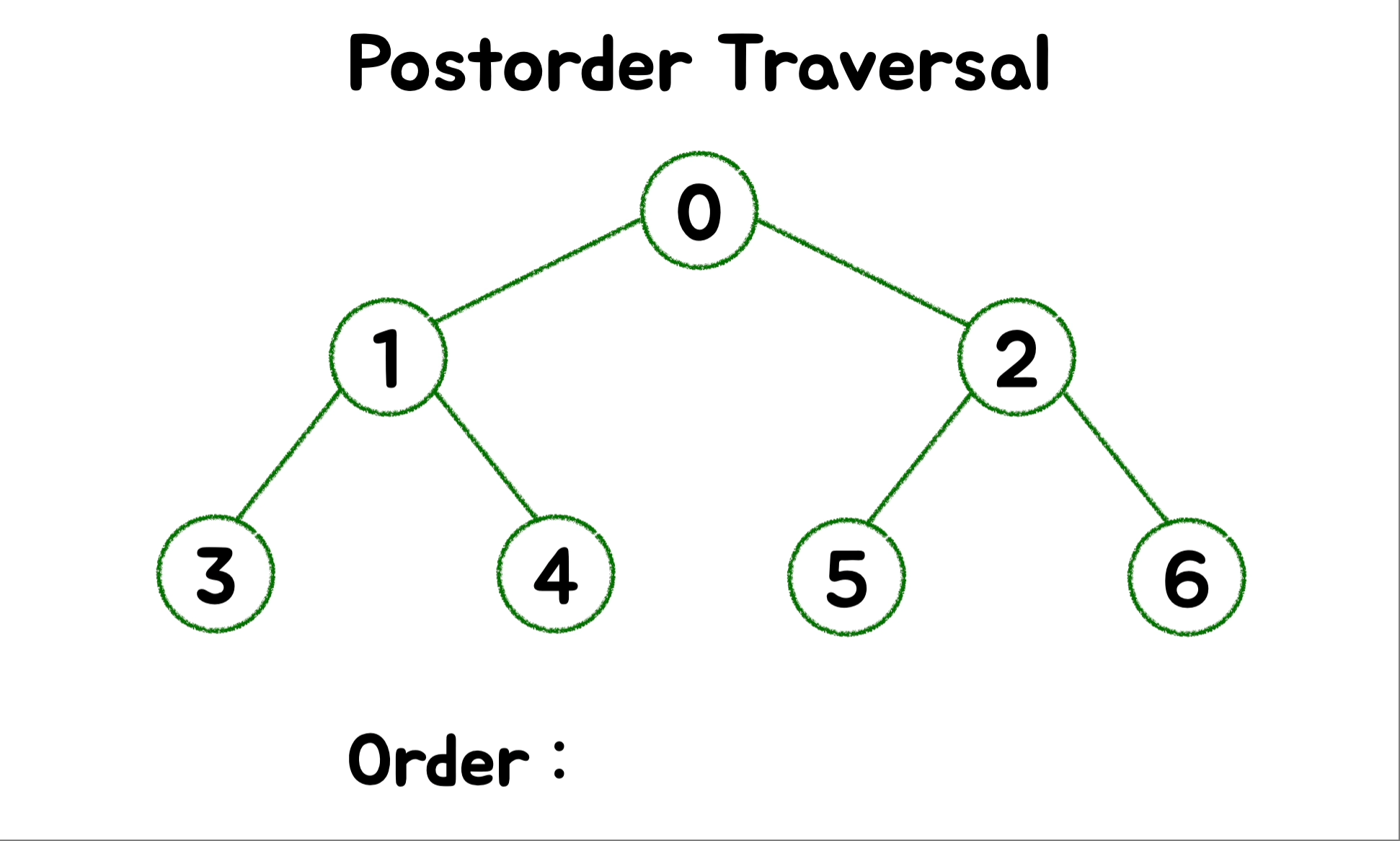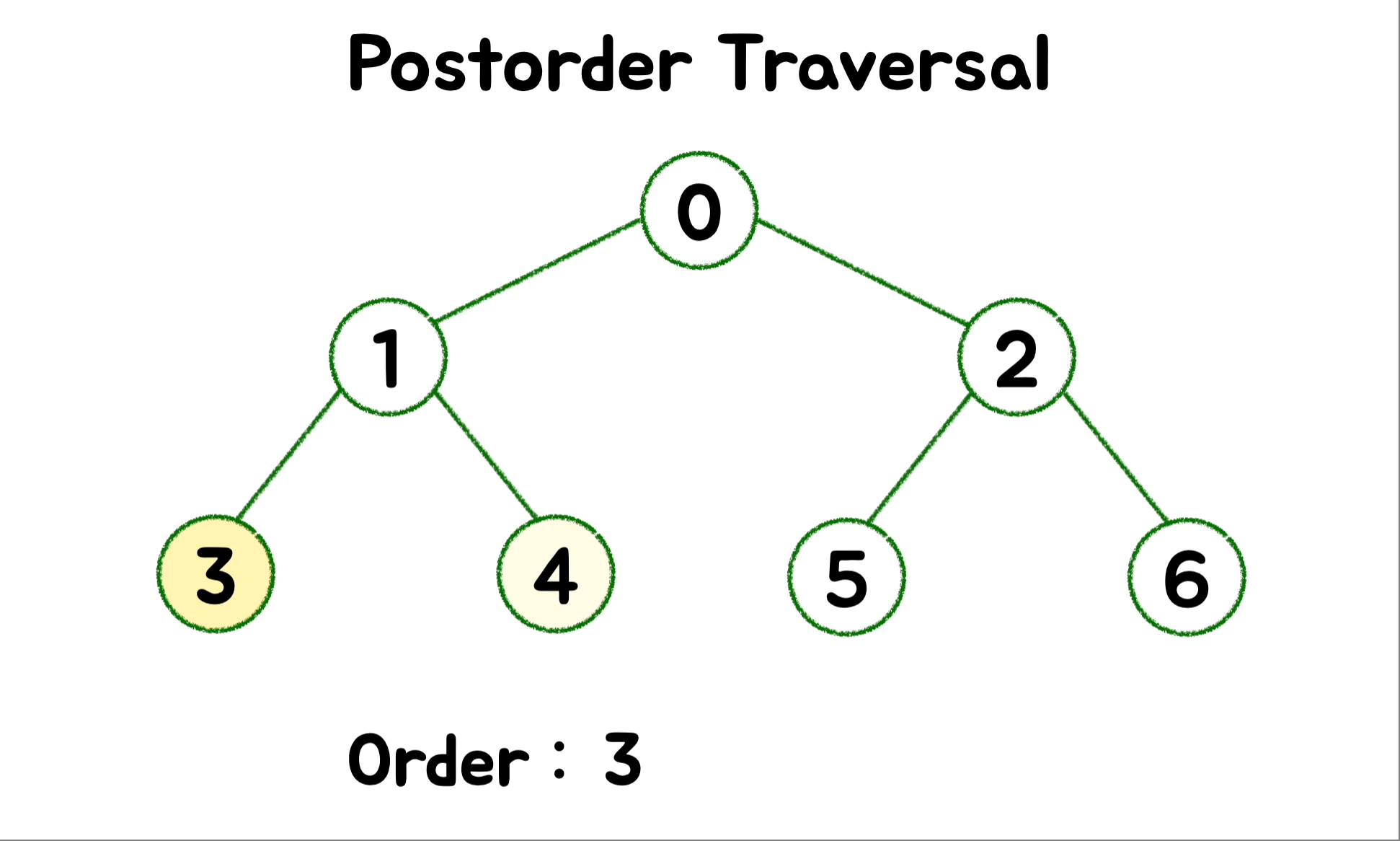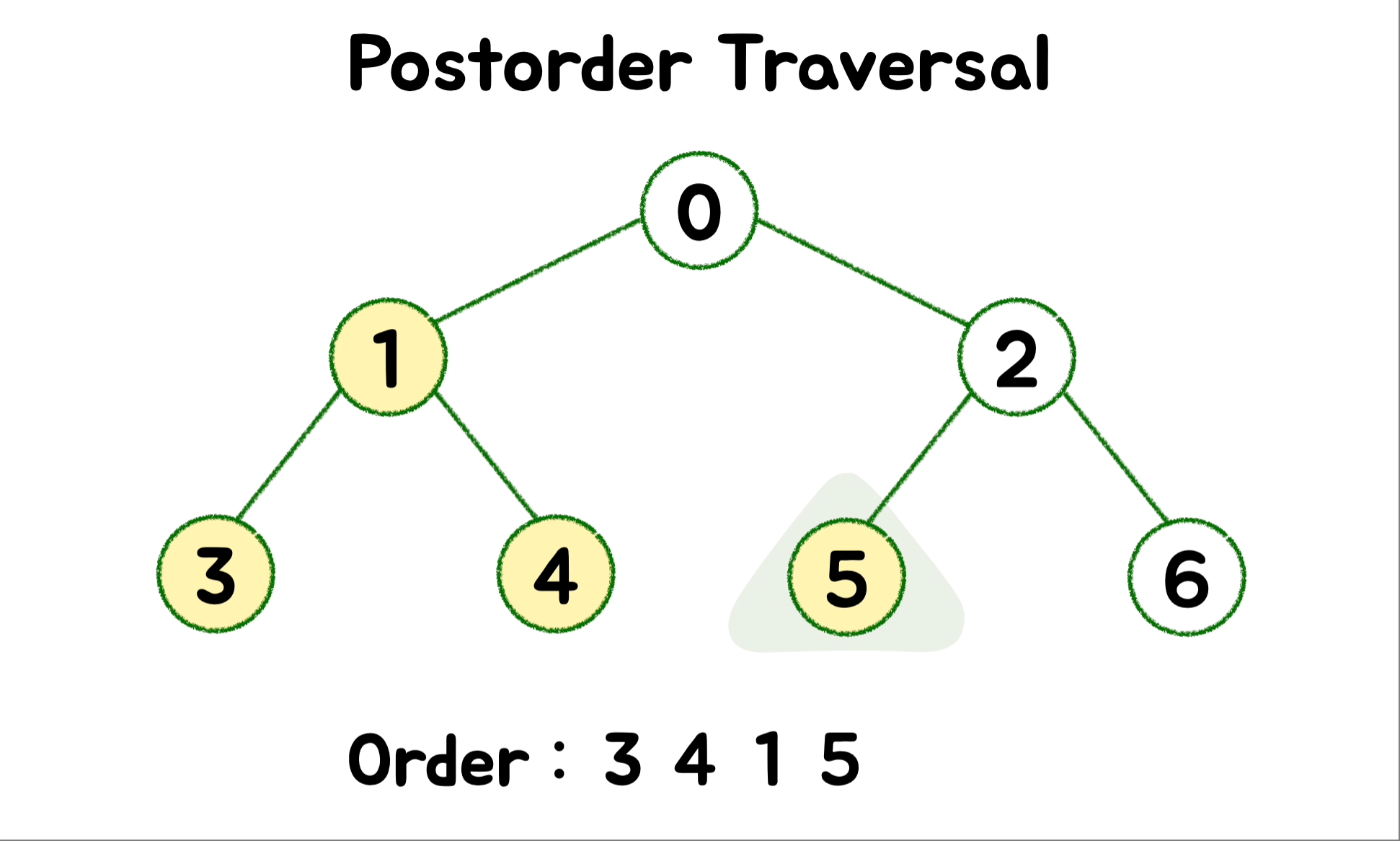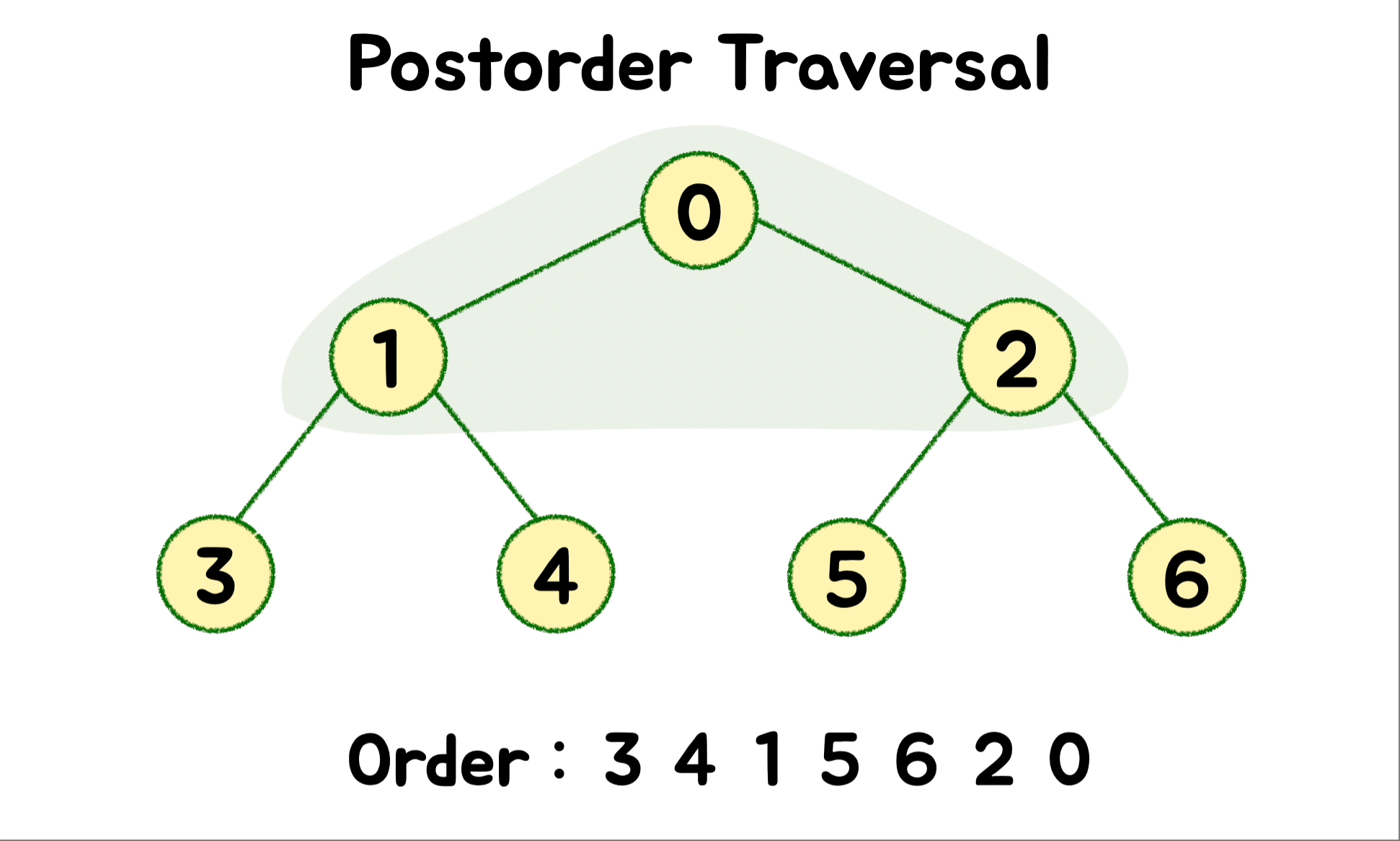
트리를 삭제하는 데 사용됩니다. 왼쪽 하위 트리를 호출해 탐색하고 이어서 오른쪽 하위 트리를 호출해 탐색합니다. 그러고 난 다음에 루트를 마지막으로 방문합니다.

let root = null;

function postorder(node) {
  if(node === null) return;
  
  let total = node.child.length;
  for(let i = 0; i < total - 1; i++) {
    postorder(node.child[i]); // left node
    postorder(node.child[total - 1]); // right node
    console.log(node.data + '-');
  }
}

🎄 BFS 트리 순회

let node = 6;
const adj = new Array(node + 1).fill(null).map(() => []);
function addEdge (node1, node2, arr) {
  arr[node1].push(node2);
  arr[node2].push(node1);
}

function printChild(root, arr) {
  const queue = [];
  queue.push(root);
  const visited = new Array(arr.length).fill(0);
  while(queue.length > 0) {
    let node = queue.shift();
    visited[node] = 1;
    for(let cur of arr[node]){
      if(visited[cur] === 0) queue.push(cur);
    console.log(`${node} 👉🏻 ${cur},`);
    }
  }
}

👀 Reference

NewHa

백 번을 보면 한 가지는 안다 👀

이전 포스트

[ ᴀʟɢᴏʀɪᴛʜᴍ ] Tree Data Structure ( 트리 )