🧩 네트워크

🎯 문제 설명

네트워크란 컴퓨터 상호 간에 정보를 교환할 수 있도록 연결된 형태를 의미합니다. 예를 들어, 컴퓨터 A와 컴퓨터 B가 직접적으로 연결되어있고, 컴퓨터 B와 컴퓨터 C가 직접적으로 연결되어 있을 때 컴퓨터 A와 컴퓨터 C도 간접적으로 연결되어 정보를 교환할 수 있습니다. 따라서 컴퓨터 A, B, C는 모두 같은 네트워크 상에 있다고 할 수 있습니다.

컴퓨터의 개수 n, 연결에 대한 정보가 담긴 2차원 배열 computers가 매개변수로 주어질 때, 네트워크의 개수를 return 하도록 solution 함수를 작성하시오.

🥅 제한 사항

• 컴퓨터의 개수 n은 1 이상 200 이하인 자연수입니다.
• 각 컴퓨터는 0부터 n-1인 정수로 표현합니다.
• i번 컴퓨터와 j번 컴퓨터가 연결되어 있으면 computers[i][j]를 1로 표현합니다.
• computer[i][i]는 항상 1입니다.

🙆🏻‍♀️ 문제 풀이

🕶️ DFS

문제를 읽자마자 DFS/BFS 문제인 만큼 DFS로 네트워크를 순회하며 부분 그래프 덩어리의 갯수를 세면 된다고 생각했다.

프로그래머스에서 주어지는 예시 대신 세 덩어리가 나오도록 테스트 케이스를 추가했다.

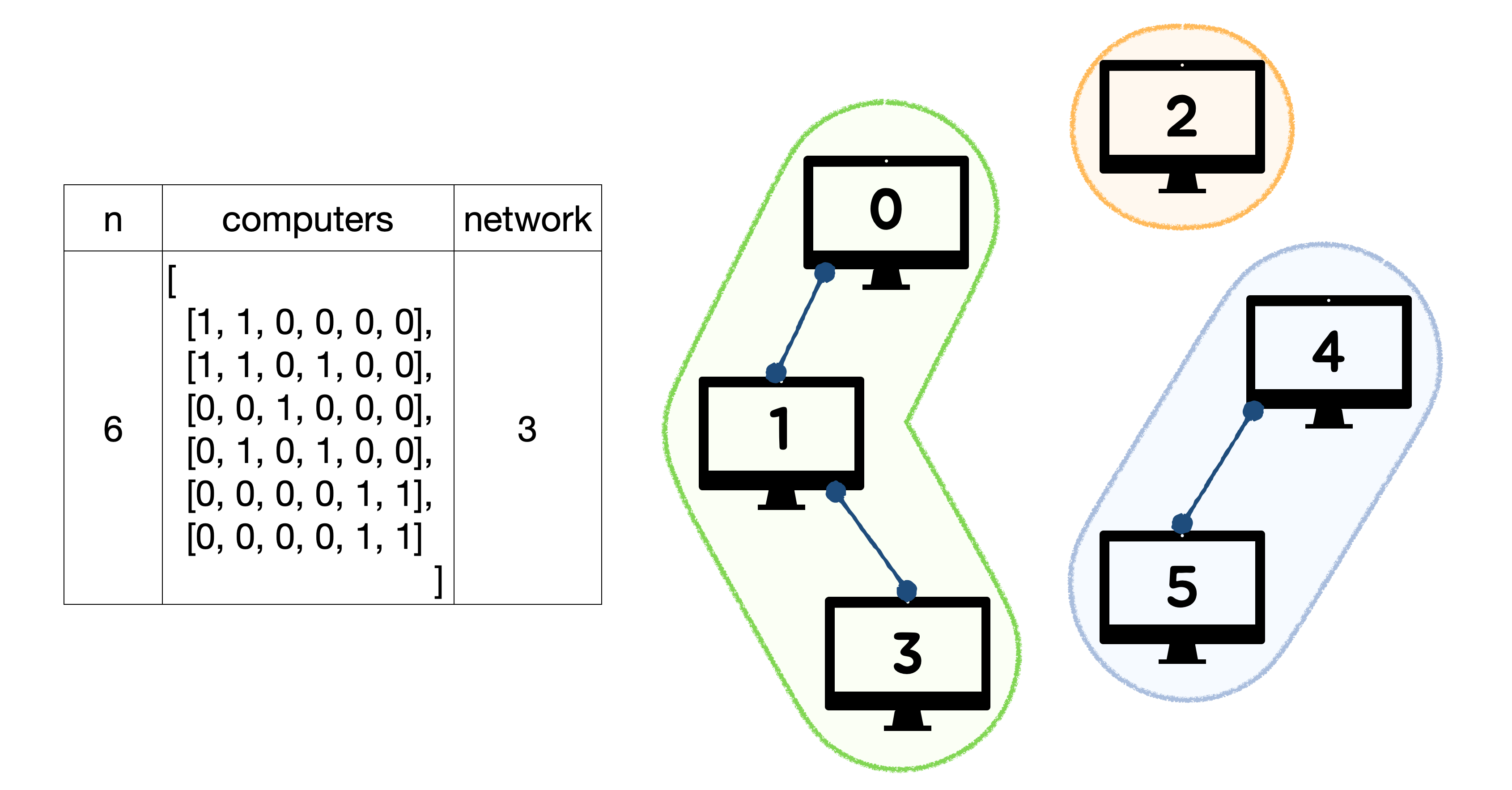
👉🏻 의사 코드

1. DFS로 컴퓨터를 순서대로 순회를 한다.
2. 순회 중간에 더이상 이어진 간선이 없어지면 하나의 덩어리이므로 network count를 1 올려준다.
3. 그 다음으로 순회하지 않은 컴퓨터를 이어서 순회한다.
4. 2~3 과정을 반복한다.
5. network count를 반환한다.

👉🏻 코드로 구현

1. DFS 순회 코드

// 우선 dfs로 간선이 이어진 부분을 탐색하는 코드를 작성.
// 0번 컴퓨터가 vertax로 들어왔을 경우를 가정하면서 작성했다.
function dfs(vertax) {
  // 방문을 표시할 배열을 하나 만든다.
  const visited = [];
  // 해당 vertax([0])를 방문표시 해준다.
  visited[vertax] = true;
  // 0번 컴퓨터의 간선들을 살피기 위해 순회 -> [1, 1, 0, 0, 0, 0]
  for(let edges = 0; edges < n; edges++){
    // 방문목록에 없고, 0번 컴퓨터와 연결된 간선이 있다(1)면
    if(!visited[edges] && computers[vertax][edges]){
		// 연결된 컴퓨터에서도 dfs를 호출해 계속해서 연결된 컴퓨터를 찾는다.
      	// 이 경우, 0번 컴퓨터의 0번 인덱스는 자기 자신으로 이미 방문표시가 되어 있으므로 넘어가고,
      	// 0번 컴퓨터의 1번 인덱스가 1이므로 dfs에 1번 컴퓨터를 넣어서 호출한다.
      	dfs(edges);
    }
  }
}

• 함수에 정점을 넣어주면 방문을 표시하고, 연결된 정점을 찾는 과정을 반복한다.

2. 방문한 컴퓨터를 제외하고 하나 하나 dfs에 넣어주도록 반복문을 돌린다.

function solution(n, computers) {
  // network count를 할 변수를 하나 만들어준다.
  let count = 0;
  // 컴퓨터 갯수만큼 루프를 돌면서
  for(let vertax = 0; vertax < n; vertax++) {
    // 방문하지 않은 정점이라면
    if(!visited[vertax]){
      // dfs를 호출한다.
      dfs(vertax)
      // 여기서 count를 세어 준다.
      count++;
    }
  }
  return count
}

• 여기에서도 visited 가 필요하므로 solution의 지역변수로 visited를 놓고, dfs를 함수 안으로 가져와야 한다.

3. 👀 최종 코드

function solution(n, computers) {
  const visited = [];
  let count = 0;
  
  function dfs(vertax) {
    visited[vertax] = [];
    
    for(let edges = 0; edges < n; edges++) {
      if(!visited[edges] && computers[vertax][edges]) {
        dfs(edges);
      }
    }
  };
  
  for(let vertax = 0; vertax < n; vertax++) {
    if(!visited[vertax]) {
      dfs(vertax);
      count++;
    }
  }
  return count
}

🕶️ BFS

DFS로 풀이가 가능하다면 BFS로도 풀 수 있다는 말이다!!

function solution(n, computer) {
  const visited = new Array(n).fill(0);
  let count = 0;
  
  function bfs(start) {
    const queue = [start];
    visited[start] = true;
    let curVertax;
    
    while(queue.length) {
      curVertax = queue.shift();
      
      for(let neighbor = 0; neighbor < n; neighber++) {
        if(!visited[neighbor] && computers[curVertax][neighbor]) {
          visited[neighbor] = true;
          queue.push(neighbor);
        }
      }
    }
  };
  
  for(let vertax = 0; vertax < n; vertax++) {
    if(!visited[vertax]) {
      bfs(vertax);
      count++;
    }
  }
  return count
}