💡 힙
최대값 혹은 최소값을 빠르게 찾기 위한 이진 트리입니다.
최소 힙의 경우에는 부모는 자식보다 작고, 최대 힙의 경우에는 부모가 자식보다 커야 합니다.
힙의 삽입과 삭제는 O(logN)만큼의 시간 복잡도를 갖습니다.
💡 이진 탐색 트리
왼쪽 자식은 부모보다 작고, 오른쪽 자식은 부모보다 큰 이진 트리가 이진 탐색 트리입니다.
이진 탐색 트리는 검색, 삽입, 삭제가 모두 트리의 높이인 O(logN~N)만큼의 시간복잡도를 갖습니다. 그래서, 트리가 편향되지 않기 위해 자가 균형 트리를 사용합니다.
💡 자가 균형 트리
이진 탐색 트리는 시간복잡도가 트리의 높이에 따라 결정되므로 편향될 경우 검색, 삽입, 삭제 과정에서 효율이 떨어집니다. 그래서 편향되지 않게 삽입과 삭제를 개선한 이진 탐색 트리를 자가 균형 트리라고 합니다. 자가 균형 트리에는 ANL 트리와 Red Black 트리가 있습니다.
💡 해시
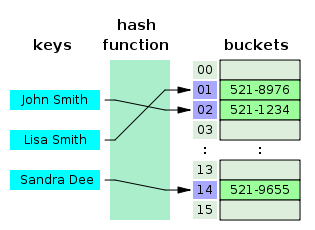
해시는 해시에 매핑하여 데이터를 저장하는 자료구조 입니다. 키는 해시함수를 통해서 해시로 변경된 다음에 value와 매핑되어서 버킷에 저장되게 됩니다. 시간복잡도는 삽입, 삭제, 조회가 모두 O(1)의 시간 복잡도를 갖습니다.
💡 해시 충돌 회피 방법
충돌 회피 기법은 해시에서, 하나의 버킷에 여러개의 데이터가 들어갈 때 그 충돌을 회피하는 방법으로, Open Addressing과 Chaining이 있습니다. Open Addressing은 다른 해시값에 저장하는 방법이고, Chaining은 해시 테이블이 원소 하나를 담는게 아니라 Linked List를 담는 방법입니다.
💡 Array(List)의 가장 큰 특징과 그로 인해 발생하는 장점과 단점에 대해 설명해주세요.
Array의 가장 큰 특징은 순차적으로 데이터를 저장한다는 점.
데이터에 순서가 있기 때문에 0부터 시작하는 index가 존재하며, index를 사용해 특정 요소를 찾고 조작이 가능하다는 것이 Array의 장점.
순차적으로 존재하는 데이터의 중간에 요소가 삽입되거나 삭제되는 경우 그 뒤의 모든 요소들을 한 칸씩 뒤로 밀거나 당겨줘야 하는 단점이 있음.
이러한 이유로 Array는 정보가 자주 삭제되거나 추가되는 데이터를 담기에 적절하지 않다.
💡 Array를 적용시키면 좋을 데이터의 예를 구체적으로 들어주세요. 구체적 예시와 함께 Array를 적용하면 좋은 이유, 그리고 Array를 사용하지 않으면 어떻게 되는지 함께 설명해주세요.
주식 차트에 대한 데이터는 요소가 중간에 새롭게 추가되거나 삭제되는 정보가 아니며, 날짜별로 주식 가격이 차례대로 저장되어야 하는 데이터.
즉, 순서가 굉장히 중요한 데이터이므로 Array 같이 순서를 보장해주는 자료구조를 사용하는 것이 좋음.
Array를 사용하지 않고 순서가 없는 자료구조를 사용하는 경우에는 날짜별 주식 가격을 확인하기 어려우며 매번 전체 자료를 읽어 들이고 비교해야 하는 번거로움이 발생.
💡 Stack과 Queue, Tree와 Heap의 구조에 대해 설명해주세요.
Stack과 Queue는 선형 자료구조의 일종, Array와 LinkedList로 구현할 수 있음.
Stack은 후입선출(LIFO)방식 즉, 나중에 들어간 원소가 먼저 나오는 구조,
Queue는 선입선출(FIFO)방식 즉, 먼저 들어간 원소가 먼저 나오는 구조.
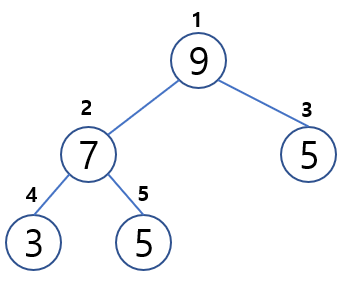
Tree는 스택과 큐와 같은 선형 구조가 아닌 비선형 자료구조이며, 계층적 관계 표현에 적합.
Heap은 최댓값 또는 최솟값을 찾아내는 연산을 쉽게 하기 위해 고안된 구조로, 각 노드의 키값이 자식의 키값보다 작지 않거나(최대힙) 그 자식의 키값보다 크지 않은(최소힙) 완전 이진 트리.
💡 선형자료구조란?
자료를 구성하는 데이터를 순차적으로 나열시킨 형태
💡 Stack과 Queue의 실사용 예를 들어 간단히 설명해주세요.
Stack - 자바의 Stack 메모리 영역
지역변수와 매개변수 데이터 값이 저장되는 공간이며 메소드 호출 시 메모리에 할당되고 종료되면 메모리가 해제되며, LIFO 구조를 가짐.
Queue - OS의 스케쥴러
자원의 할당과 회수를 하는 스케줄러 역할을 큐가 할 수 있음.
메모리에 적재된 다수의 프로세스 중 어떤 프로세스에게 자원을 할당할 것인가 그 순서를 결정할 때 가장 단순한 형태의 스케쥴링 정책이 선입 처리 즉, 큐라고 볼 수 있음.
💡 Priority Queue(우선순위 큐)에 대해 설명해주세요.
우선순위 큐는 들어간 순서에 상관없이 우선순위가 높은 데이터를 먼저 꺼내기 위해 고안된 자료구조.
우선순위 큐 구현 방식에는 배열, 연결 리스트, 힙이 있고, 그 중 힙 방식이 시간 복잡도를 O(logN)을 보장하기 때문에 일반적으로 완전 이진 트리 형태의 힙을 이용해 구현.
💡 Array와 ArrayList의 차이점에 대해 설명해주세요.
Array는 크기가 고정적이고, ArrayList는 크기가 가변적.
Array는 초기화 시 메모리에 할당되어 ArrayList 보다 속도가 빠르고,
ArrayList는 데이터 추가 및 삭제 시 메모리를 재할당하기 때문에 속도가 Array보다 느림.
💡 Array와 LinkedList의 장/단점에 대해 설명해주세요.
Array는 인덱스로 해당 원소에 접근할 수 있어 찾고자 하는 원소의 인덱스 값을 알고 있으면 O(1)에 해당 원소를 접근할 수 있음. 즉, RandomAccess가 가능해 속도가 빠름.
하지만 삽입 또는 삭제의 과정에서 각 원소들을 옮겨줘야 하는 비용이 생겨 이 경우 시간 복잡도는 O(N)이 된다는 단점.
이 문제점을 해결하기 위한 자료구조가 LinkedList. 각각의 원소들은 자기 자신 다음에 어떤 원소인지만을 기억하고 있기 때문에 이 부분만 다른 값으로 바꿔주면 삽입과 삭제를 O(1)로 해결.
하지만 원하는 위치에 한 번에 접근할 수 없다는 단점. 연결되어 있는 링크를 따라가야만 접근이 가능하여 접근속도가 느림.
Array는 검색이 빠르지만 삽입, 삭제가 느림.
LinkedList는 삽입, 삭제가 빠르지만, 검색이 느림.
💡 해시 테이블(Hash Table)과 시간 복잡도에 대해 설명해주세요.
해시 테이블은 (key, value)로 데이터를 저장하는 자료구조 중 하나로 빠르게 데이터를 검색할 수 있는 자료구조.
빠른 검색 속도를 제공할 수 있는 이유는 내부적으로 배열(버킷)을 사용하여 데이터를 저장하기 때문.
각 Key값은 해시함수에 의한 고유한 index를 가지게 되어 바로 접근할 수 있으므로 평균 O(1)의 시간 복잡도로 데이터를 조회. 하지만 index값이 충돌할 경우 Chanining에 연결된 리스트들까지 검색해야 하므로 O(N)까지 증가할 수 있음.
💡 Hash Map과 Hash Table의 차이점에 대해 설명해주세요.
사용 방법도 거의 동일하지만, 차이점이 있음
동기화 지원 여부와 null 값 허용 여부의 차이가 있음.
- 해시 테이블(Hash Table)
- 동기화를 지원하여, Thread-safe 함.
- HashMap에 비해 느리다. (다른 스레드가 block되고 unblock 되는 대기 시간을 기다리기 때문)
- key값이나 value값에 null이 들어갈 수없다.
- 해시 맵(Hash Map)
- 동기화를 지원하지 않아, Thread-safe 하지 않음.
- Hashtable과는 다르게 synchronized 키워드가 없음
- key 값이나 value 값에 null이 들어갈 수 있음.
💡 BST(Binary Search Tree)와 Binary Tree에 대해 설명해주세요.
이진트리는 자식 노드가 최대 두 개인 노드들로 구성된 트리.
이진 탐색 트리는 이진 탐색과 연결 리스트를 결합한 자료구조.
이진 탐색의 효율적인 탐색 능력을 유지하면서, 빈번한 자료 입력과 삭제가 가능하다는 장점.
이진 탐색 트리는 왼쪽 트리의 모든 값은 반드시 부모 노드보다 작아야 하고, 오른쪽 트리의 값은 부모 노드보다 커야 하는 특징이 있음.
이진 탐색 트리의 탐색 연산은 트리의 높이에 영향을 받아 높이가 h일 때 시간 복잡도는 O(h)이며, 트리의 균형이 한쪽으로 치우쳐진 경우 worst case가 되고 O(n)의 시간 복잡도를 가짐.
이런 worst case를 막기 위해 나온 기법이 RBT(Red-Black Tree)
💡 RBT(Red-Black Tree)에 대해 설명해주세요.
BST를 기반으로 하는 트리 형식 자료구조, RBT는 BST의 삽입, 삭제 연산 과정에서 발생할 수 있는 문제점을 해결하기 위해 만들어짐.
스스로 균형을 잡는 트리.
BST를 기반으로 하기 때문에 당연히 BST의 특징을 모두 가짐.
노드의 child가 없을 경우 child를 가리키는 포인터는 NIL 값을 저장. 이러한 NIL들을 leaf node로 간주.
모든 노드를 발간색 또는 검은색으로 색칠하며, 연결된 노드들은 색이 중복되지 않음.
모든 노드는 red 혹은 black
루트 노드는 black
Nil s노드는 black
red의 자녀들은 black -> red가 연속적으로 존재할 수 없음.
