Table
저장되는 데이터는 키(key)와 값(value)이 하나의 쌍을 이루는 자료구조를 테이블이라고 한다. 테이블에서 키(key)가 존재하지 않는 '값'은 저장할 수 없다. 그리고 모든 키는 중복되지 않는다. 테이블은 사전구조 혹은 맵(map)이라 불리기도 한다.
탐색연산에 O(1)의 시간복잡도를 가진다.
ex) 아파트의 우편함 - 호수(key), 우편물(value)
ex) 사전(dictionary) - 단어(key), 단어에 대한 설명 혹은 내용(value)
typedef struct_empInfo {
int empNum; //직원의 고유번호 : key
int age; // 직원의 나이 : value
} EmpInfo;
EmpInfo empInfoArr[1000]; // 직원들의 정보를 저장하기 위해 선언된 배열위의 배열을 테이블이라고 하기에는 조금 부족한 감이 있다. 왜냐하면 테이블은 키를 결정하였다면, 이를 기반으로 데이터를 단번에 찾을 수 있어야 하기 때문이다. 즉, 테이블에서 키(key)는 데이터를 찾는 도구이다.
EmpInfo ei;
empInfoArr[ei.empNum] = ei; // 저장
ei = empInfoArr[eNum]; // 탐색테이블의 키(key)값인 empNum을 인덱스 값으로 하여 그 위치에 데이터를 저장할 수 있어야 한다.
여기서 문제는 직원이 999999999999이라면 매우 큰 배열이 필요하게 되는데 어떤 문제가 생길까?
- 직원 고유번호의 범위가 배열의 인덱스 값으로 사용하기에 적당하지 않다.
- 직원 고유번호의 범위를 수용할 수 있는 매우 큰 배열이 필요하다.
이 문제들을 해결해주는 것은 해시 함수이다.
Hash Table
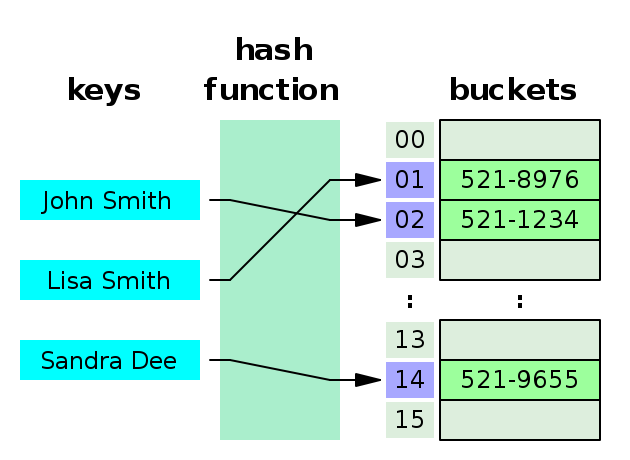
Hash Table은 연관배열 구조를 이용하여 키(key)에 값(value)을 저장하는 자료구조이다. 키(key)는 해시함수를 통해 해시로 변경이 되며 해시는 값과 매칭되어 저장소에 저장이 된다.
연관배열 구조(associative array) : 키 1개와 값 1개가 1:1로 연관되어 있는 자료구조이다. 따라서 키(key)를 이용하여 값을 도출할 수 있다.
구조
- 키(key) : 고유한 값. 해시 함수의 input이 된다. 다양한 길이의 값이 될 수 있다. 이 상태로 최종 저장소에 저장이 되면 다양한 길이 만큼의 저장소를 구성해 두어야 하기 때문에 해시 함수로 값을 바꾸어 저장이 되어야 공간의 효율성을 추구할 수 있다.
- 값(value) : 저장소(bucket, slot)에 최종적으로 저장되는 값으로 키와 매칭되어 저장, 삭제, 검색, 접근이 가능해야 한다.
- 해시 함수(Hash Function) : 키(key)를 해시(hash)로 바꿔주는 역할을 한다. 다양한 길이를 가지고 있는 키(key)를 일정한 길이를 가지는 해시(hash)로 변경하여 저장소를 효율적으로 운영할 수 있도록 도와준다. 다만, 서로 다른 키(key)가 같은 해시(hash)가 되는 경우를 해시 충돌(Hash Collision)이라고 하는데, 해시 충돌을 일으키는 확률을 최대한 줄이는 함수를 만드는 것이 중요하다.
- 해시(Hash) : 해시 함수(Hash Function)의 결과물이며, 저장소(bucket, slot)에서 값(value)과 매칭되어 저장된다.
해시함수 예시
typedef struct_empInfo {
int empNum; //직원의 고유번호 : key
int age; // 직원의 나이 : value
} EmpInfo;
int getHashValue(int empNum) {
return empNum % 100;
}
위의 코드와는 다르게 직원의 고유번호를 입사년도 네자리와 입사 순서 네자리로 구성한다고 예를 들어보자. 언젠가는 천명을 넘어설 수 있겠지만 현재에는 백명 이상을 채용할지도 모르는 상황이다. 따라서 배열 길이의 최소화를 위해 노력한다는 가정으로 getHashValue함수를 통해 해시를 얻는다.
hash function을 통해서 넓은 범위의 키를 좁은 범위의 키로 변경하였다. 하지만 20210103과 20120003의 고유번호를 가진 직원이 있다면 03이라는 값은 해시를 가지게 되는 문제가 생기게 된다. 이러한 상황을 충돌(Collision)이라고 한다.
삽입(Insertion)
- 시간복잡도 : O(1)
최악의 경우 O(n)이 될 수 있음..
삭제(Deletion)
- 시간복잡도 : O(1)
최악의 경우 O(n)이 될 수 있음..
탐색(Search)
- 시간복잡도 : O(1)
최악의 경우 O(n)이 될 수 있음..
해시 충돌(Hash Collision)
충돌만 아니라면 해시 테이블은 삽입,삭제,탐색 과정에서 모두 평균적으로 O(1)의 시간복잡도를 가지고 있는 효율적인 자료구조이다.

John Smith와 Sandra Dee의 hash가 같다. 이러한 상황을 Hash Collision이라고 한다. 비둘기 집의 원리로 이러한 상황은 필연적으로 나타난다.
- 비둘기 집의 원리 : n+1개의 비둘기가 n개의 비둘기 집에 들어간다면 적어도 1개 이상의 비둘기 집에 2마리 이상의 비둘기가 있을 것이다.
해시 충돌 해결 방법
닫힌 어드레싱 방법
Chaining
닫힌 어드레싱 방법(closed addressing method)이다. 닫힌 어드레싱 방법은 무슨일이 있어도(충돌이 발생해도) 자신의 자리에 저장한다는 뜻이다.
이것이 가능하게 하려면 값을 저장할 자리를 여러개 마련하는 수밖에 없다. 여러 개의 자리를 마련하는 방법으로는 배열을 이용하는 방법과 연결 리스트를 이용하는 방법이 있다.
하지만 배열은 충돌이 발생하지 않을 경우 메모리 낭비가 심하고 충돌의 최대 횟수를 결정해야 하는 부담이 있으므로 연결 리스트를 이용하여 슬롯을 연결하는 방법이 닫힌 어드레싱 방법을 대표한다.
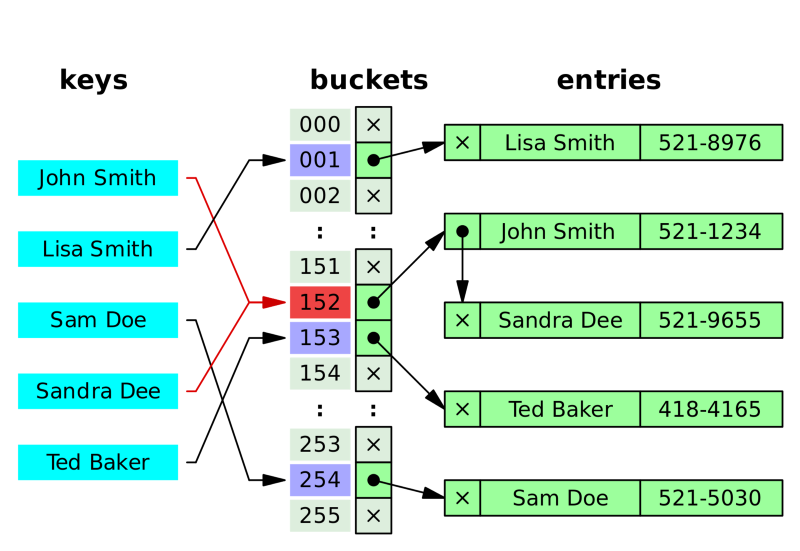
Sandra Dee의 값이 153에 들어가려고 하는데 이미 값이 있다. 그래서 기존의 John Smith값 뒤에 연결시켰다.
즉, 체이닝은 자료 저장시, 저장소(bucket)에서 충돌이 일어나면 해당 값을 기존 값과 연결시키는 기법이다.
상대적으로 적은 메모리를 사용한다는 장점이 있지만 한 해시에 자료들이 계속 연결된다면(쏠림현상이 생긴다면) 검색 효율이 낮아진다는 단점이 있다.
in Java
HashMap vs HashTable
동기화 지원 여부의 차이가 있다.
// 해시테이블의 put
public synchronized V put(K key, V value) {
// Make sure the value is not null
if (value == null) {
throw new NullPointerException();
}
// Makes sure the key is not already in the hashtable.
Entry<?,?> tab[] = table;
int hash = key.hashCode();
int index = (hash & 0x7FFFFFFF) % tab.length;
@SuppressWarnings("unchecked")
Entry<K,V> entry = (Entry<K,V>)tab[index];
for(; entry != null ; entry = entry.next) {
if ((entry.hash == hash) && entry.key.equals(key)) {
V old = entry.value;
entry.value = value;
return old;
}
}
addEntry(hash, key, value, index);
return null;
}
// 해시맵의 put
public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}병렬 처리를 하면서 자원의 동기화를 고려해야 하는 상황이라면 해시테이블(HashTable)을 사용해야 하며, 병렬 처리를 하지 않거나 자원의 동기화를 고려하지 않는 상황이라면 해시맵(HashMap)을 사용하면 된다.
열린 어드레싱 방법(open addressing method)
충돌이 발생하면 다른 자리에 대신 저장한다. 열린 어드레싱 방법은 해시를 찾는 규칙에 따라 3가지로 구분된다.
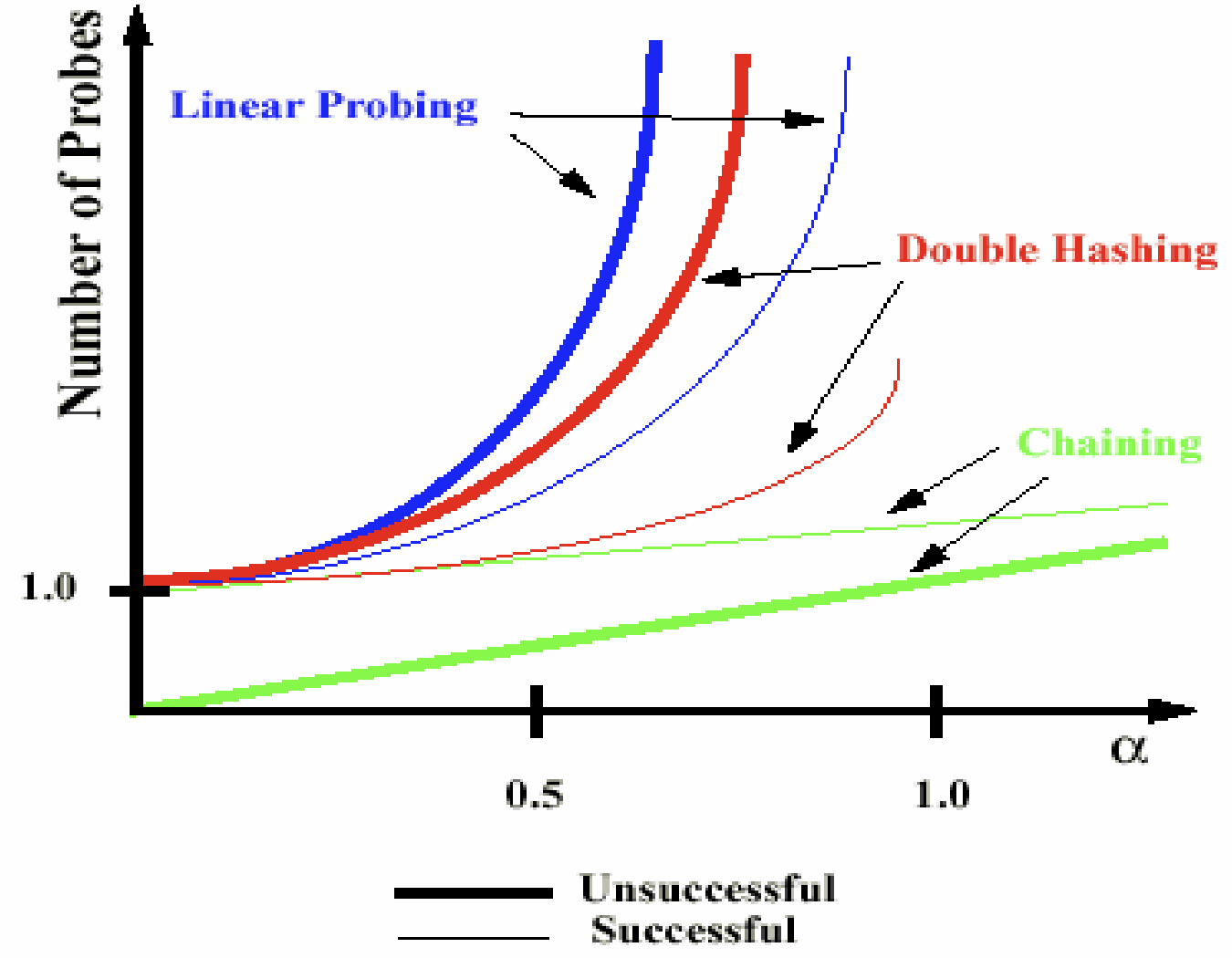
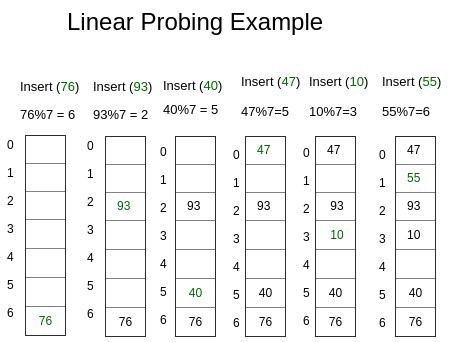
1. 선형 조사법(Linear Probing)

충돌이 발생했을 때 그 옆자리가 비었는지 살펴보고, 비었을 경우 그 자리에 대신 저장하는 방법이다. 옆자리가 비어있지 않을 경우, 한칸 더 이동을 해서 자리를 살피게 된다. 즉 f(k)+1 -> f(k)+2 -> f(k)+3 ...으로 전개된다. 하지만 선형 조사법은 충돌의 횟수가 증가함에 따라서 클러스터 현상이 발생한다는 단점이 있다.
2. 이차 조사법(Quadratic Probing)
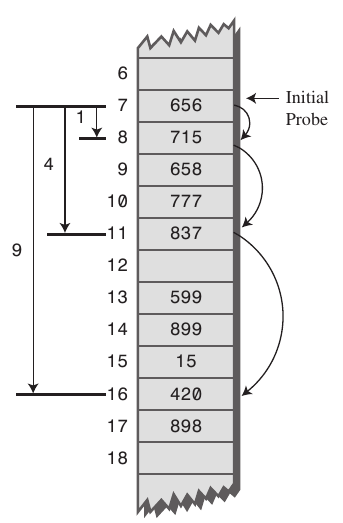
선형 조사법의 단점을 극복하기 위해서 고안된 방법이다. 충돌이 발생하면 좀 멀리서 빈 공간을 찾는 방법이다. f(k)+1^2 -> f(k)+2^2 -> f(k)+3^2...순으로 전개된다.
3. 이중 해사(Couble Hashing)
이차 조사법도 해시 값이 같다면 충돌 발생시에 빈 슬롯을 찾기 위해서 접근하는 위치가 늘 동일하다는 문제점이 있다. 선형 조사법 보다는 낫지만 접근이 진행되는 슬롯을 중심으로 클러스터 현상이 발생할 확률은 여전히 높다.
이차 조사법은 좀 멀리서 빈 공간을 찾기는 하지만 그 빈 공간을 선택하는 방법은 한칸, 네칸, 아홉칸..과 같이 규칙적이다. 이렇게 빈 공간을 찾는 방법을 불규칙적으로 구성하는 것이 이중해시 방법이다. 두개의 해시 함수를 쓰기 때문에 붙여진 이름이다.
- 1차 해시 함수 : 키를 근거로 저장위치를 결정하기 위한 것.
- 2차 해시 함수 : 충돌 발생시 몇칸 뒤를 살필지 결정하기 위한 것.
비교