큰 수의 법칙과 중심극한정리 이해,파이썬 실습

큰 수의 법칙, 중심극한정리 파이썬 실습!

큰 수의 법칙(Law of Large Numbers)

모집단에서 표본을 추출하여 평균을 구할때 그 표본의 크기가 클수록 표본평균이 모평균과 같아지는 것을 말한다.

중심극한정리(Central Limit Theorem)

표본의 크기가 충분히 크면 모집단의 표본과 무관하게 표본평균의 확률분포는 정규분포를 따른다는 것을 말한다.

여기서 큰 수의 법칙과 중심극한정리가 애매모호하게 비슷한듯 다른듯 느껴진다. 내가 헷갈렸던 것을 기반으로 설명을 해보자면 큰 수의 법칙은 정의 그대로 한 개의 표본의 크기자체를 계속해서 늘려갈때 그 하나의 표본의 평균이 모평균과 같아지는 것이다.

수학적으로 나타내자면 표본의 크기가 n, 표본의 평균을 X_var, 모평균을 E(x) 모평균의 분산을 var(x) 라 할때 다음과 같은식이 n이 커질때 N(0,1)인 가우시안 분포, 정규분포를 따른다 라고 할 수 있다. 아래 내용은 실습에 필요하기때문에 간단히 언급했다.

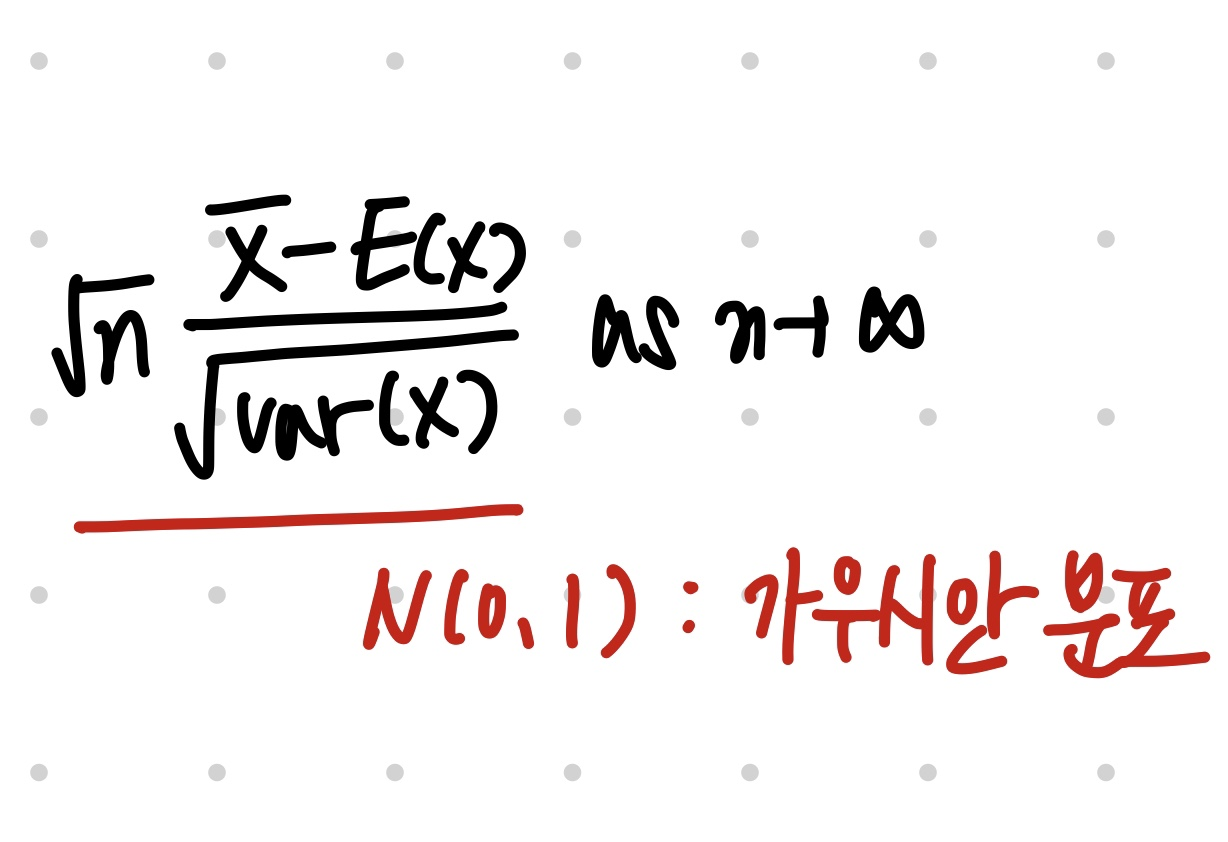
다만 이해하기 쉽게 생각해보자면 크기가 n개인 표본의 평균을 X1이라 하면 또 다른 크기가 n개인 표본의 평균을 X2,X3 , ... XN개를 모아봤더니 그 분포가 정규분포를 따른다고 생각하면 이해가 쉽다. 실제로 간단한 실험을 진행할때 위와 같은 내용으로 실습하여 확인해볼 것이다.

LLN in python

큰 수의 법칙을 파이썬을 통해 간단히 확인해보자.
표본의 크기를 n으로 두고 for문을 통해 n을 점차 증가시켰을때 표본의 평균을 그래프를 통해 확인해볼 것이다. 모집단은 심플한 uniform distribution을 이용했다.

파이썬 코드는 다음과 같다.

n = np.arange(10,1000000,1000)
s_mean = np.zeros(len(n))
for i in range(len(n)):
   x = np.random.uniform(size = n[i])
   s_mean[i] = x.mean()
s_mean
import matplotlib.pyplot as plt
plt.plot(s_mean,'-')
plt.ylim((0.49,0.51))

코드를 간단히 설명하자면 먼저 표본의 크기인 n을 10부터 1000000까지 1000간격으로 생성해준다. 그리고 sample mean을 저장할 공간 s_mean을 생성해준다. 그럼 for문을 사용하기 위한 준비는 끝이다. 이후 for 문에서 모집단인 uniform 분포에서 표본평균을 뽑아준다. 그러면 끝이다 그래프를 그리기위해 matplotlib를 이용하여 그래프를 그려주면 다음과 같은 결과가 나온다.

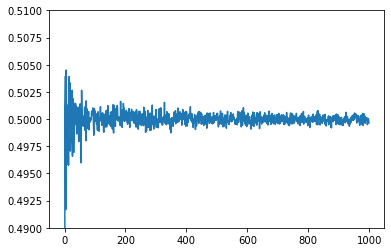
그래프를 확인해보면 n이 점차 증가하면서 uniform분포의 평균인 0.5로 수렴하는 형태를 보이는 것을 알 수 있다. 이처럼 간단한 실습이 끝났다.

CLT in python

큰 수의 법칙을 확인해봤으니 중심극한정리를 파이썬을 활용해 간단하게 확인해보자. 중심극한정리 또한 uniform분포를 이용할 것이다. 물론 정의에 따라 어떤 다른 분포를 이용하여 실습해보더라도 실습이 가능하다!

uniform분포는 분포 특성상 n이 비교적 크지않아도 금새 정규분포를 따른다. 따라서 n=2인경우와 n=20인경우를 확인해보겠다.

n_e = 100000   
n = 20    
z = np.zeros(n_e)
for i in range(n_e):
   k = np.random.uniform(size = n)
   z[i] = np.sqrt(n)*(k.mean()-0.5)/np.sqrt(1/12)
plt.hist(z, bins = 100)

여기서 n과 n_e가 헷갈릴 수 있는데 n은 표본의 크기 n_e는 표본평균의 개수라고 생각하면 된다. 위의 중심극한정리 설명과 비교해서 코드를 살펴보기 바란다. n__e는 단순히 분포의 모습을 보이기위해서 큰 수를 잡은 것이지 중심극한정리와는 상관성이 없다고 생각하면 이해가 편하다. 그리고 위에 간단히 언급한 식을 작성해주면 된다. 나머지 코드는 큰 수의 법칙과 유사하다. (혹시 이해가 가지않는 부분이 있다면 댓글 달아주시면 답변드리겠습니다.!)

n=2,n=20인경우 코드의 결과는 다음과 같다.

n=2

n=20

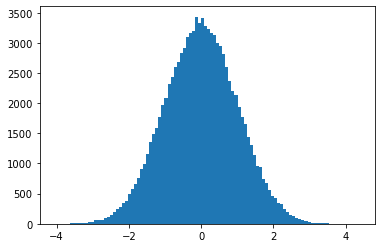
n=20 인 분포가 정규분포와 매우 흡사하게 나타나는 것을 알 수 있다.

내용에 의문이 가는 부분이 있거나 오류가 있다면 댓글로 알려주시면 감사하겠습니다!