This is my own translation for Adrien Lucas Ecoffet's An Intuitive Explanation of Policy Gradient. I focused on conveying the meaning. Please beware, I often used completely different words.
Adrien Lucas Ecoffet의 An Intuitive Explanation of Policy Gradient 한국어 의역 입니다. 의역이니깐, 다른 단어를 쓰고 문장에 뉘앙스나 문장 자체를 바꿨습니다. 왜냐하면 정보 전달이 중요한 것 이지, 번역이 중요한게 아니니깐요.
참고로 (s | a)와 (a | s)가 뒤바뀐 공식들은 그냥 (s | a)로 통일 하시면 됩니다. 모두 (s | a)인게 맞습니다.
총 3파트에 거쳐서 Policy Gradient 할 것 입니다. 다음은 A2C이고 시간이 주어진다면 off-policy policy gradient에 대해 다뤄보겠습니다. (역자: 2022/01/22 시점에서도 파트 2,3은 나오지 않음.)
여기서 나온 코드는 여기 깃헙에서 확인 하실수 있습니다.
Introduction
기존 설명의 문제점
최근에 꽤나 성공적인 강화학습 알고리즘은 Policy-Gradient이라는 알고지즘 패밀리에 속합니다. A3c, TRPO, PPO...등이 있겠네요. 정확히는 actor-critic 알고리즘 패밀리에 속합니다. 찐 강화학습 팬이라면 policy gradient는 당연히 알아야 겠죠. 근데 알려고 해도 제대로 된 설명이 별로 없습니다. 다들 뭔가 부족하게 설명합니다.
다른 설명들은 아래와 같은 수학공식을 들이밀고 제대로 된 설명을 못합니다.
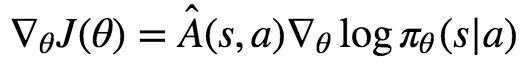
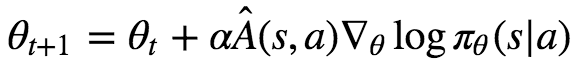
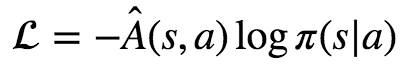
공식을 이해하려면 직관적인 설명 부터 해야되는데 말이죠. 심지어 제가(Adrien Lucas Ecoffet) 좋아하는 강화학습 튜토리올도 사정은 비슷합니다. Jaromiru은 'A3C 만들어보아요'에서 설명은 이러합니다.
Expection안에 있는 ∇θlogπ(a|s)은 어떤 방향이 policy를 높혀주는지 알려줍니다. 쉽게 말하면 현재 컨택스에서 어떻게 하면 해당 action의 확률을 높혀주는지를 알려줍니다.
Arthur Juliani은 'Tensorflow를 쓰는 강화학습'에서 아래와 같이 설명했습니다.
직관적으로 이 loss 함수는 reward를 증가 시키는 action 파라미터는 높히고 반대는 줄이는 것 입니다.
두 설명 모두 부족하죠. 특히 로그가 왜 들어가 있는지 설명 하지 못합니다. 이런 '직관적인' 설명으로는 절대로 혼자서 loss 함수를 알 수 없습니다. 누가 한번 'loss 함수 써봐' 라고 하면 못쓰겠죠.
놀랍게도 이 공식에 직관적인 설명이 있습니다. 바로 강화학습의 교과서인 Reinforcement Learning: An Introduction, Sutton & Barto에 Chapter 13, section 3에 설명 되어 있습니다. (역자: 실제로는 저기서도 제대로된 설명 없음)
제가 이제 설명을 제대로 해드릴텐데요. 설명을 다 듣고 나면 왜 log가 나오는지 부터 해서 자기만의 policy gradient도 만드실수 있으실 겁니다. 물론 다 이해를 하신다면요.
설명을 이해 하시려면 반드시 일반적인 강화학습 개념을 아셔야 됩니다. DQNs까지는 아니더라고 Q-Learning는 아셔야 됩니다.
만약 Q-Learning과 DQNs 대해 잘 모르시면, 아래 튜토리얼을 추천해 드립니다.
- 역자 강력추천: 쉬운 풀이 Sung Kim 유튜브 쉬운 풀이로 개념을 이해하게 되면 수학 공식 유도나 뒷부분 내용의 이해가 빨라진다. 꼭 먼저 보길 바란다.
- 제가(Adrien Lucas Ecoffet) 쓴 '딥강화학습으로 Atari 도장깨기'
- Jaromiru의 'DQN을 만들어 봅시다'
- Arthur Juliani의 'Tensorflow를 쓰는 강화학습'
Policy Gradient의 장점
왜 쓰는지는 알고 가야 겠죠?
- Q-Learning에서 policy는 고정되어 있다. 이러면 stochastic(랜덤) policy를 학습을 못합니다. 몇몇 환경에서는 좋을 수 있으나, 이러면 저희가 직접 exploration 전략을 짜야 합니다. 그래서 보통 ϵ-greedy exploration 쓰는데 굉장히 비효율적일 때가 있죠.
- Q-Learning에서 쉽게 연속적인 actions 다룰수 없습니다. 반대로 policy gradient에서는 쉽죠.
- 이름에서 알 수 있수 있듯, policy gradient는 policy의 기울기를 업데이트 하면서 policy를 향상 시킵니다. 반대로, Q-Learning은 action에 대한 value의 예측치를 업데이트 합니다. 간접적으로만 policy를 업데이트를 합니다. 당연히 policy를 직접 업데이트 하는게 더 맞겠죠? 보통 맞습니다.
일반적으로 policy gradient 쓰는게 DQNs 처럼 value-based 방법 쓰는 것 보다 좋습니다. 특히 Atari 게임 문제 처럼 최신 문제에서는요.
Policy Gradient 설명
Simple Policy Gradient Ascent
설명을 할 때 최소한의 수학으로 설명 하겠습니다.
π는 policy 입니다. 예를 들어 πθ(a|s)는 state s가 주어졌을 때 action a를 취할 확률을 뜻합니다. 여기서 θ는 policy에 parameters를 말합니다. 다른말로는 neural network에 weights이죠.
우리의 최종 목표는 θ를 업데이트 하여 πθ를 최적화 하는 것 입니다. 여기서 θ가 지속적으로 변화 표기는 이렇게 하겠습니다. θt의 다음은 θt+1 입니다.
보통 action이 연속적이지 않고 각각 끊어져(이산) 있으면, πθ는 softmax가 되어 있는 output unit일 것 입니다. 그래서 output은 각 action의 대한 확률 입니다. (역자: 해당 내용 별 필요 없음. 왜 넣었는지 모르겠음)
당연하게도 만약 a*이 최적의 action이라면 πθ(a∗|s)은 1에 가깝게 하는게 우리가 원하는 것 입니다.
이렇게 하기 위해서는 πθ(a∗|s)에 gradient ascent을 해야 겠죠. 한번 반복 할 때 마다 아래와 같이 θ를 업데이트 해줄것 입니다.

∇πθt(a∗|s)는 πθt(a∗|s)을 편미분(∇)하는 걸 뜻 합니다. 가장 기울기가 가파른 쪽으로 θt을 업데이트 해줘야겠죠. 이건 딥러닝이 하는 방식과 똑같습니다. 물론 ascent이니깐 높은 쪽으로 선택해야 겠죠.
최적 a∗ 쪽으로 계속 policy를 업데이트 한다고 보셔도 됩니다.
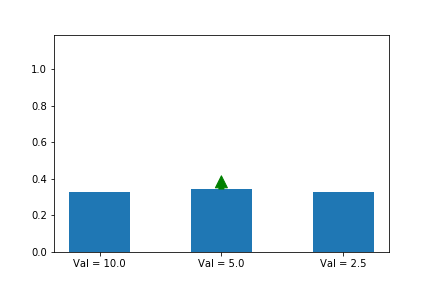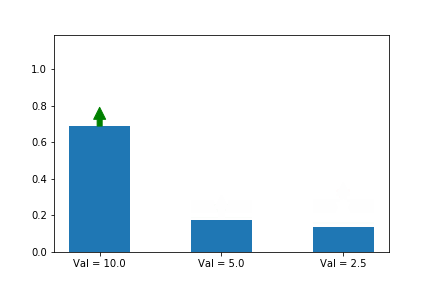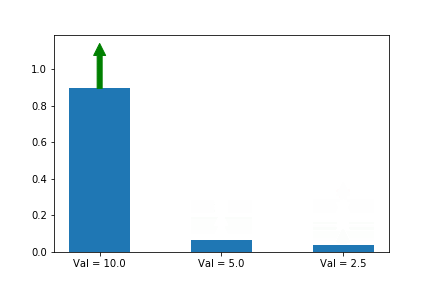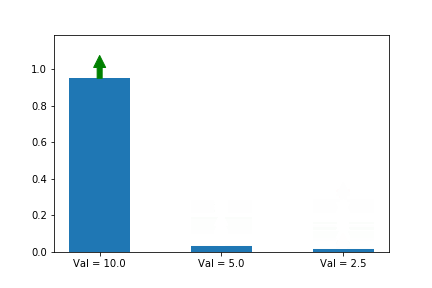
아래 예시를 보시죠. 보기 쉽게 state를 한개로만 정합시다. 그리고 첫번째 action이 최적의 action으로 가정 합시다. 그래서 a*에 대해서 gradient ascent 합니다.

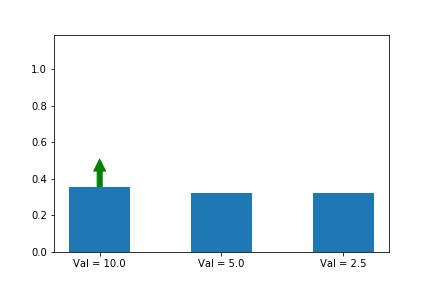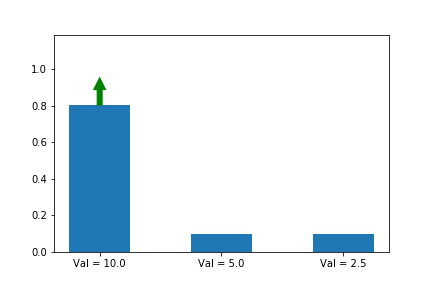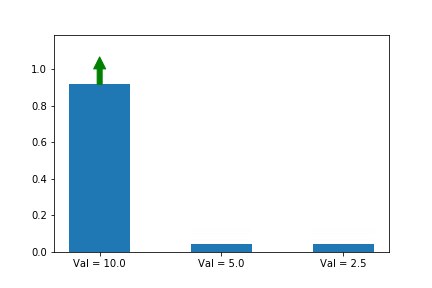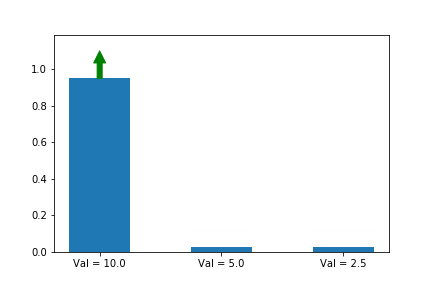
y이 축은 각 action의 확률 입니다. 화살표는 업데이트 할 때 마다 어떤 action 기울기를 선택 했는지 알려줍니다. 여기서는 첫번째 action만 선택 했네요. 공고룝게도 value가 10으로 3중 가장 크군요. 그리고 첫번째 action 확률은 다른 확률들과 상관 관계에 있군요.
Gradients 정하기
첫번째 예시 처럼 최적의 action을 바로 아는 경우는 드뭅니다. 왜냐하면 바로 그것이 결국 우리가 구하고자 하는 거 자나요!
만약 최적의 action을 모른다면 다른 action을 선택하여 업데이트 하게 되어 policy가 수렴하지 않을 수도 있겠네요.
해결책이 하나 있습니다. 바로 우리의 예측치에 비례하여 업데이트 하는 것 입니다. 여기서 저희가 예측 하는 것은 Q(s,a) 입니다. 그리고 예측치는 각각 Val= 10.0, Val = 5.0, Val = 2.5 으로 써져 있네요. 계속 업데이트 하다보면, 결국 a*가 1로 확실하게 수렴하는 것 입니다.
특별하게 Q(s,a)를 Q̂ (s,a)로 부르겠습니다. 왜냐하면 예측 하는 것 이니깐요. 결국 Q-Learning가 똑같습니다. 다른 점이 몇가지 있는데 뒤에서 다루도록 하죠. 그리고 이해를 돕기 위해 지금 시점에서는 Q 함수가 주어졌다고 가정 합시다.
이제 위 공식과 조금 다르게 나오겠네요.
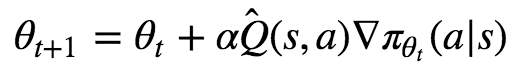
조금 바보 같지만 한번 해봅시다. 우리는 각 action에 대한 정보를 압니다. Val = 10.0, Val = 5.0, Val = 2.5 처럼 말이죠. 그런데 어떤 action이 제일 좋은지 모른다는 걸 가정 합니다. (당연히 10.0가 그 중 제일 크다는 건 알지만, 모른다고 합시다.)그러면 당연히 첫번째, 두번째, 세번째 중 random하게 선택을 하면서 아래와 같이 업데이트를 행할 것 입니다. 그래도 결국 첫번째 action이 a*으로 선정 됐군요.

On-Policy 보정
On-Policy란 무작위로 action을 선택 하는게 아니라 현재 어떤 Policy가 최적인지 예측한 걸 업데이트 하는 것을 말합니다. 바로 맨 위 첫번째로 한 방법과 같습니다. 근데 물론 첫번째를 예측 하지 못하면 전혀 다른 방향으로 수렴하겠네요.
On-Policy로 하는 두가지 이유가 있습니다.
- 트레이닝 할 때도 더 많은 reward를 모을 수 있습니다.
- 확률 높은 state 범위를 explore 하게 됩니다. 바로 현재 생각하고 있는 최적 actions 예측치를 사용해서 말이죠.
한번 해볼까요? 시작을 [0, 0, 1.5] 을 두고 하겠습니다.

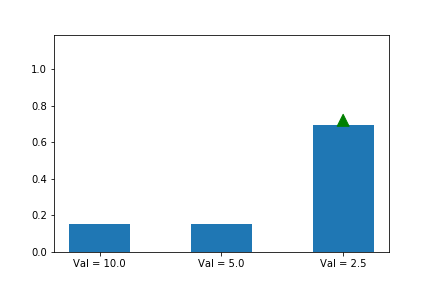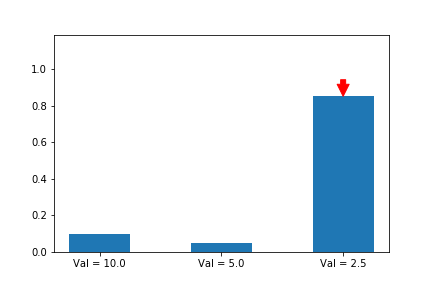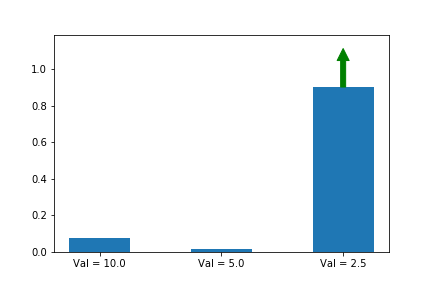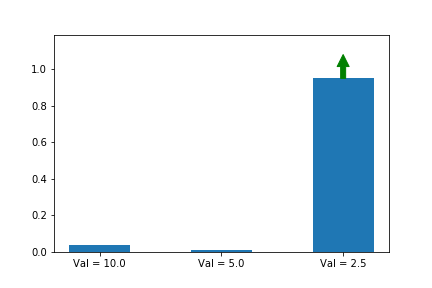
역시 이니셜라이즈 할 때 잘못하니 전혀 다른 방향으로 수렴했군요. 만약 [0, 1.0, 0] 으로 했으면 두번째 action으로 수렴했겠네요.
이걸 고치려면 어떻게 할까요? 한가지 방법은 이렇습니다. 한번의 선택이 많은 영향 보다는 적은 영향을 끼치게 하고 그 선택을 더 자주 하게 하면 어떨까요? 이렇게 개선을 하려면 어떻게 해야 할까요? 쉽습니다. 바로 action의 확률로 나눠 버리면 됩니다. 아래의 공식과 말이죠.
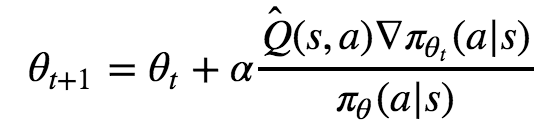
한번 해봅시다.

시작을 [0, 0, 1.5] 을 두고 하는 것은 동일 합니다.
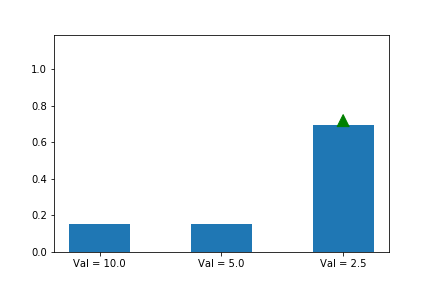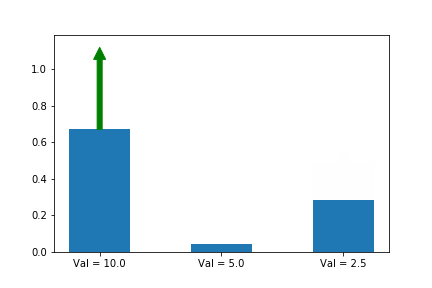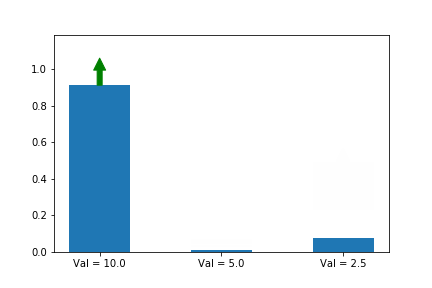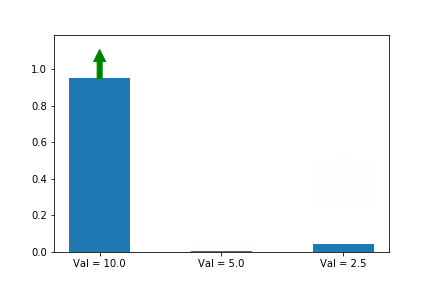
잘됐네요! 3번째 action이 시작할 때는 더 유리했는데, 결국 우리가 원하는 1번째 action으로 최적화가 이뤄납니다. 직관적인 설명은 이정도로 됐죠?
기본 REINFORCE
아니 잠시만요! 아직 설명이 다 끝난 거 같지 않은데요? 공식에서 왜 로그가 나오는지도 설명 안하셨자나요. 여기서는 A가 나오고 Q는 안나와요.
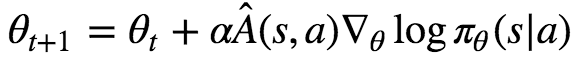
저는 다 설명했습니다. 장난이고요. 사실 두 공식의 핵심 개념은 모두 같습니다.

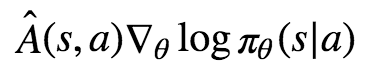
다음 섹션에서 Â와 Q̂를 차이를 말할것 입니다. 근데 사실 둘중 뭐를 써도 괜찮습니다. Â를 쓰는 이유는 조금더 최적화를 하기 위함 입니다.
그럼 이제 log에 대해서 말해 볼까요? calculus에서 배운걸 기억 하시면 아실 수 있습니다. 바로 체인룰과 log x의 미분이 1 / x 라는 사실을 기억 하시면요.
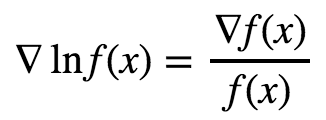
자 이제 log가 어디서 나왔는지 아시겠죠? 그럼 왜 강화 학습 교수들은 log가 들어간 공식을 더 선호 할까요? 두가지 이유가 있습니다.
- 더 어려워 보이면 있어 보이자나요. (역자: 진담반 농담반임 강화학습 교과서 보면 쉽게 설명 할 수 있는 것을 굳이 어렵게 설명하는 경향이 있음. Sung Kim 홍콩 과기대 교수님처럼 있는 그대로를 보여주는 분이 많이 필요함)
- log 형식으로 바꾸면 여러 딥러닝 라이버리에서 사용 할 수 있게 합니다. L=−Â(s,a)logπθ(s|a) 처럼 말이죠. Â(s,a)는 θ에 대한 상수이니 loss 함수 안으로 옴겨도 됩니다.
이 시점에서는 REINFORCE 기본 개념 설명은 다했습니다. REINFORCE가 어떤걸 stands 하는지 아시죠? REINFORCE는 “REward Increment = Nonnegative Factor × Offset Reinforcement × Characteristic Eligibility”… 입니다. (리얼임 이 링크 가보세요) REINFORCE이 모든 policy gradient 알고리즘에 기초 입니다.
...
tbc in part (2/2)
역자: 그 다음 내용은 중요하지 않아서 나중에 하겠습니다. 먼저 간단히 설명 하겠습니다. Q̂ 과 Â 차이를 간단히 설명하면 Â = Q̂ - V 입니다.

와 좀 더 주목을 받을만한 글이라고 생각합니다. 지금까지 본 글중에 가장 직관적이었어요. 좋은 예시와 같이 잘 설명해주셔서 감사합니다.