그래프 탐색 알고리즘 - DFS & BFS (feat. 구현코드)

구현 코드 (Codesandbox)
TypeScript iterative DFS (stack)
TypeScript recursive DFS (call stack)
TypeScript iterative BFS (queue)

Graph(그래프) 란?
그래프 탐색 알고리즘
DFS vs BFS 간단 비교
DFS (Depth-First-Search)
ㄴ DFS - Iteration (Stack)
ㄴ DFS - Recursion (Call Stack)
BFS (Breadth-First-Search)
ㄴ BFS - Iteration (Queue)

DFS와 BFS는 대표적인 그래프 탐색 알고리즘이다.

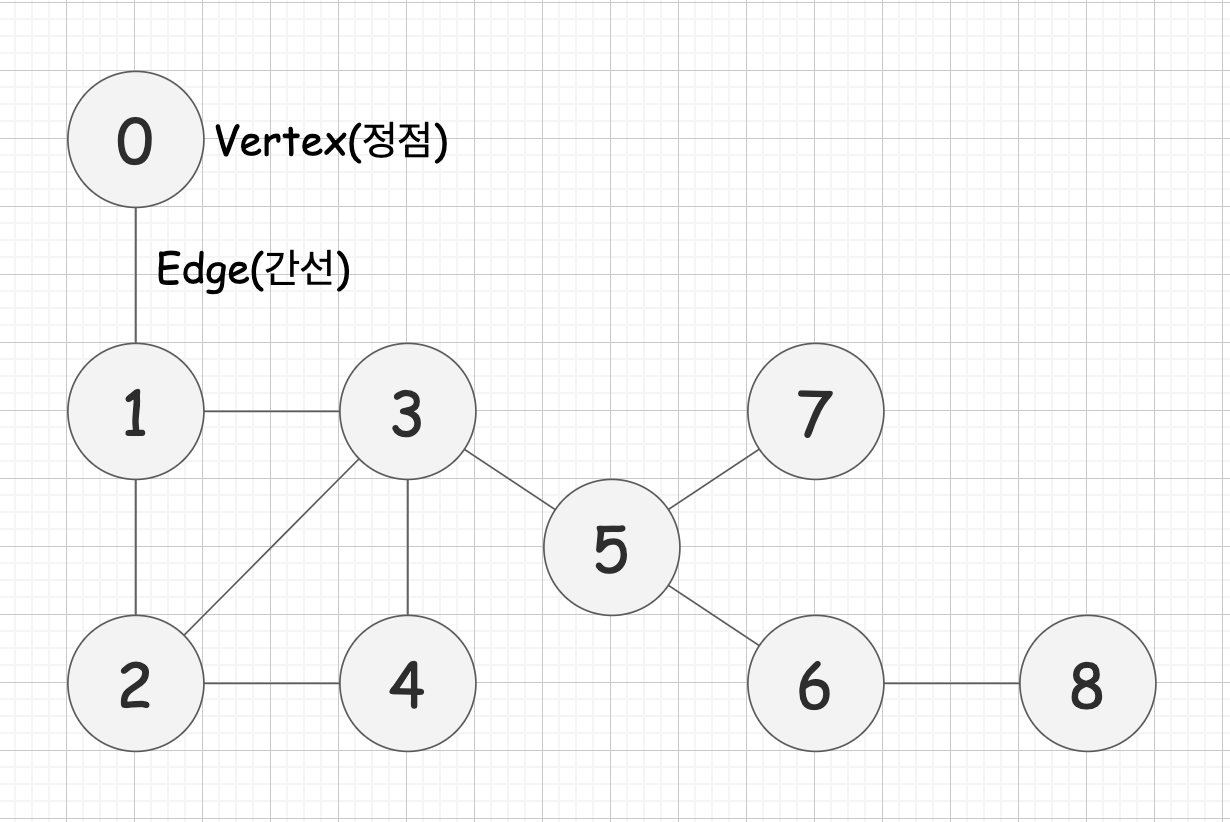
Graph(그래프) 란?

• 정점(Vertex)과 간선(Edge)으로 구성된 자료구조다.
• 각각의 지점을 정점이라고 하고,
• 정점과 정점을 연결을 간선이라고 한다.
• 간선은 일방향일 수 있고 비용이 다를 수 있다.

그래프 탐색 알고리즘

• 그래프 데이터 구조에서 특정한 정점(Vertex)을 찾거나 간선(Edge)으로 연결된 모든 정점들을 방문하는 알고리즘
• 대표적인 그래프 탐색 알고리즘 두 가지:
  • DFS(Depth-First-Search)
  • BFS(Breadth First Search)

그래프 탐색으로 풀 수 있는 문제

• 경로탐색 유형 (최단거리, 최단시간)
• 네트워크 유형 (연결)
• 조합 유형 (모든 조합 만들기)

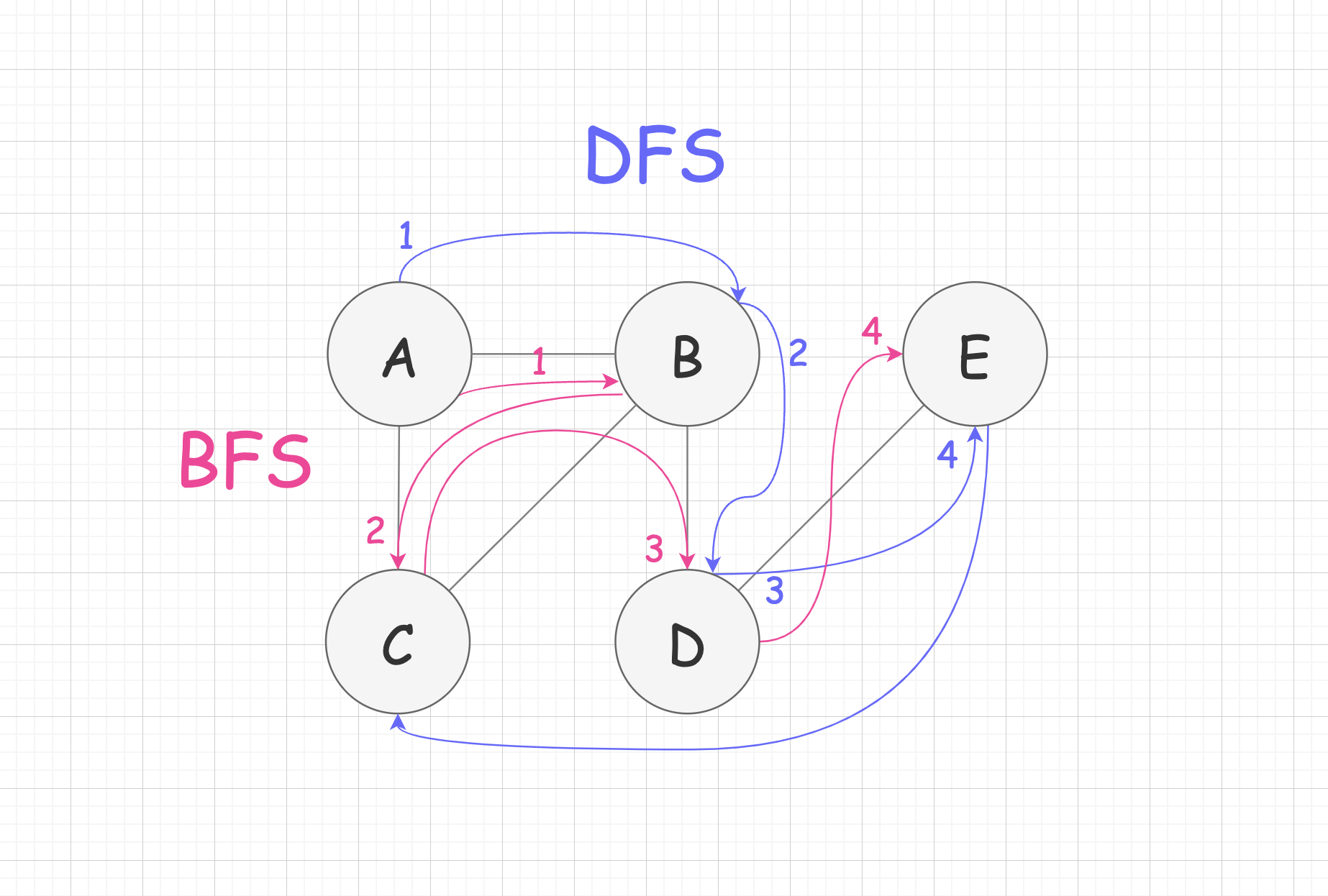
DFS vs BFS 간단 비교

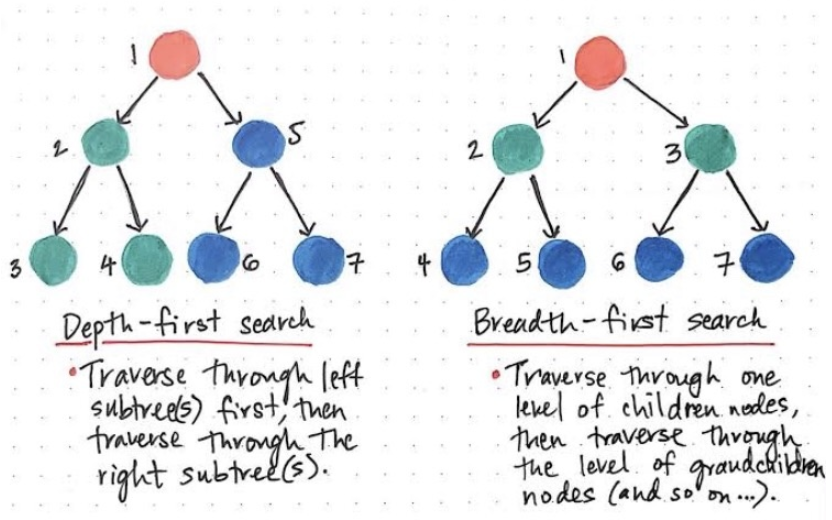
• 이미지출처 : https://iancoding.tistory.com/329
• DFS, BFS로 이진트리를 탐색하는 과정 비교
• 1 > 2 > 3 > 4 > 5 > 6 > 7 순서로 탐색한다.

DFS (Depth-First-Search)

• 루트 노드에서 시작해 다음 분기로 넘어가기 전 해당 분기를 완벽하게 탐색
  • 한 분기에서 더 이상 탐색할 곳이 없을 때 이전 경로로 돌아가서 다음 분기로 넘어간다.
• Iteration(Stack), Recursion(CallStack)을 사용
• 트리 탐색에서 inorder, preorder, postorder 가 DFS에 속한다.
  • 트리의 경우 마지막 자식 노드까지 탐색 후, 형제 노드를 탐색
  • https://www.geeksforgeeks.org/tree-traversals-inorder-preorder-and-postorder/

시간복잡도

인접 리스트

• V(정점 수) E(간선 수)
• DFS는 총 V번 호출된다.
• 모든 정점들을 한 번씩 방문, 모든 간선을 한번씩 모두 체크했다고 가정 시
• O(V + E)

DFS 탐색 진행 방식 간단 예시

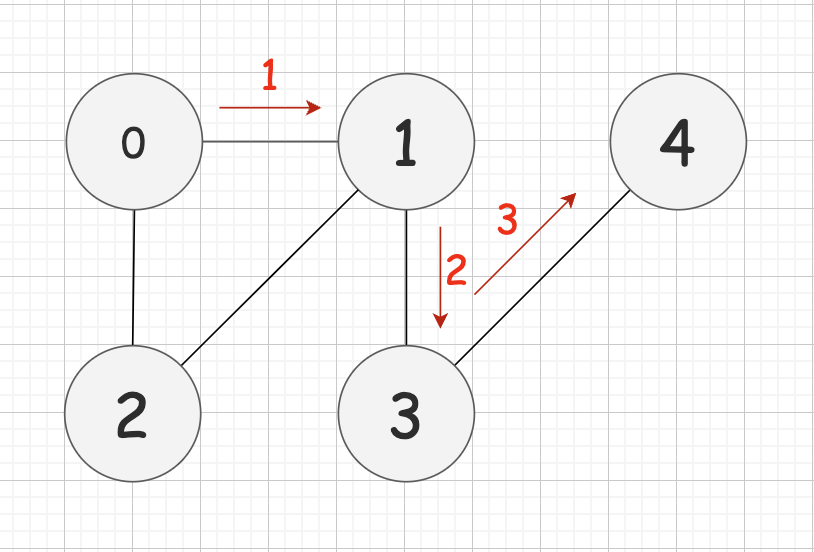
• 탐색을 시작한 분기를 끝까지 탐색한다. 0 > 1 > 3 > 4 > 2

DFS 장단점

장점

• 최선의 경우, 가장 빠른 알고리즘이다. 운 좋게 한 번에 올바른 경로를 선택한다면, 최소 실행 시간에 정답을 찾을 수 있다.
• 찾으려는 노드의 depth가 깊다면, BFS보다 빠르게 찾을 수도 있다.

단점

• 최악의 경우, 가능한 모든 경로를 탐색해야한다.
• 특정 분기만 지나치게 Depth가 깊다면, 효율이 굉장히 안좋을 수 있다.
  • 정답이 바로 앞에 있는데 뺑 돌아가는 경우가 있을 수 있다.
  • 스택오버플로우
• 재귀 함수를 이용할 경우
  • 재귀가 깊어지면 메모리 비용을 예측하기 어렵다.
• 찾은 경로가 최단 경로라는 보장이 없다.

DFS - Iteration (Stack)

그래프 구조 & 탐색 순서

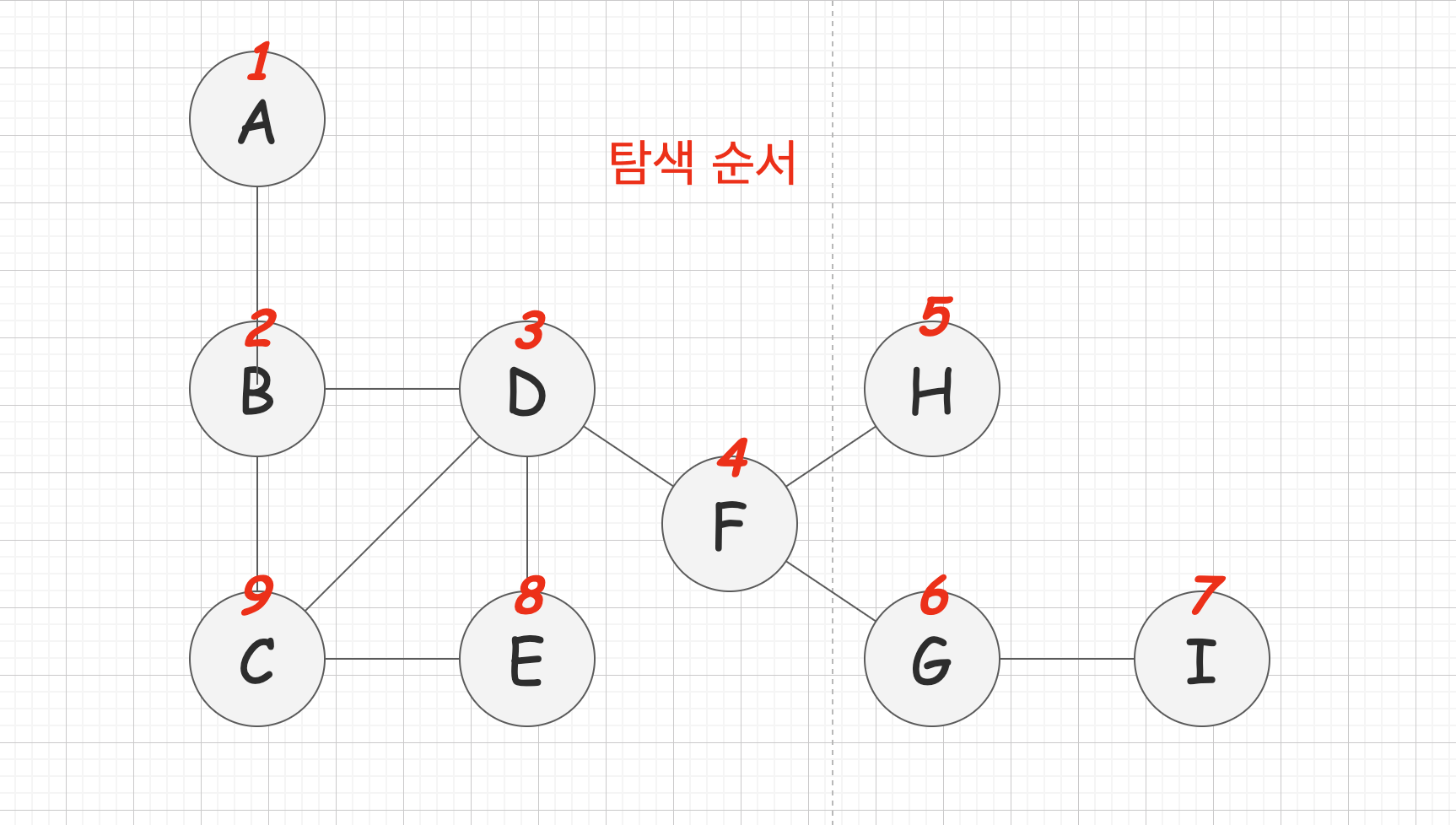
탐색 과정

1. 시작 Node를 Stack에 추가
2. Stack에서 Node를 꺼내기(방문)
3. 꺼낸 Node에서 연결된 Node들을 전부 Stack에 추가
   • 연결된 Node는 알파벳 순으로 Stack에 추가
   • 이미 방문한 노드는 Stack에 추가 X
4. 꺼낸(방문한) Node를 출력

• 위 과정을 반복

구현 코드

• 탐색 시작 노드를 선택할 수 있음

DFS - Recursion (CallStack)

그래프 구조 & 탐색 순서

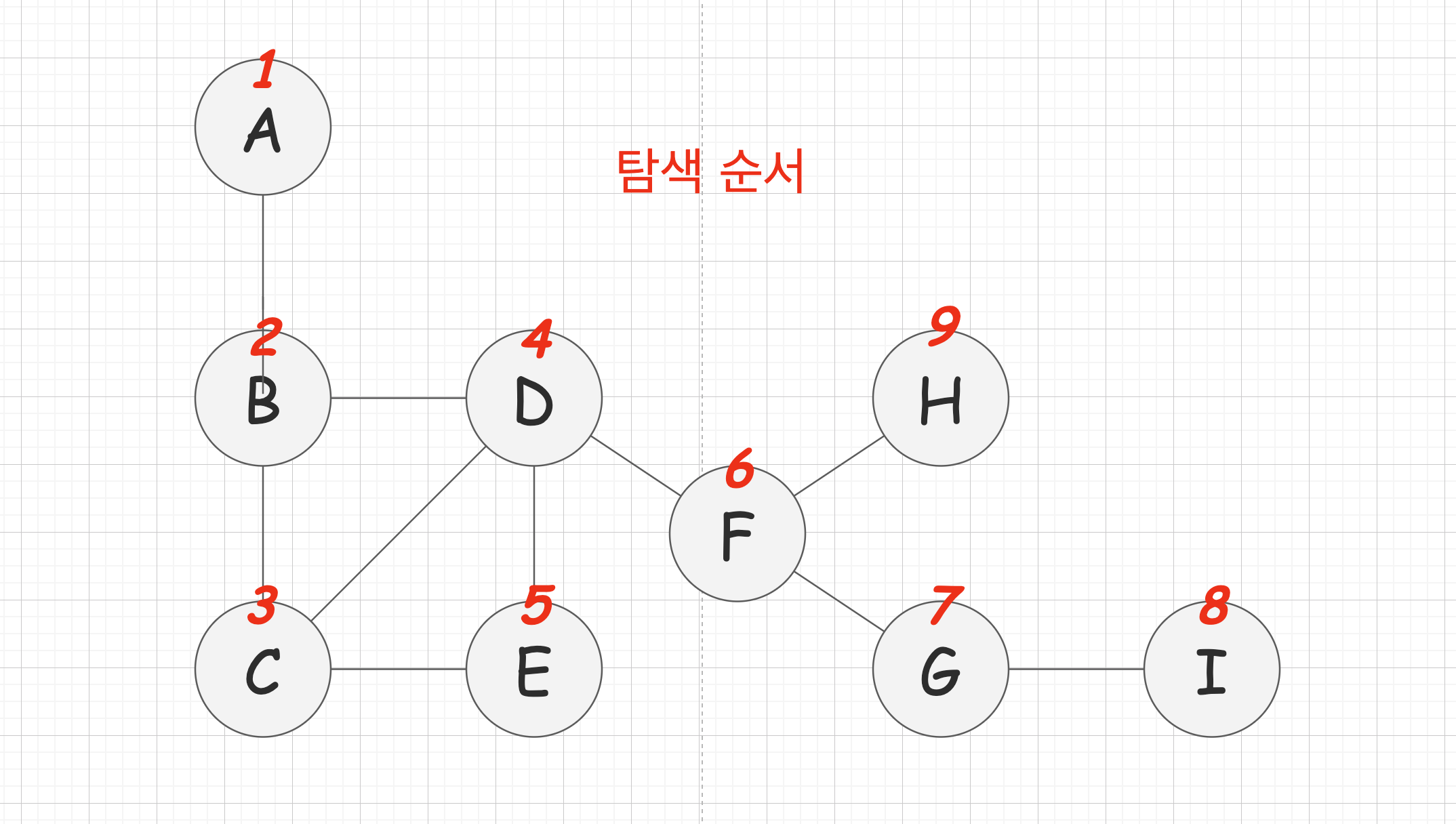
탐색 과정

1. 시작 Node를 인자로 dfs함수 호출 (callStack 생성)
   • 방문한 Node를 출력
2. 방문한 Node에서 연결된 Node들을 dfs함수 재귀 호출
   • 연결된 Node는 알파벳 순으로 dfs함수 재귀 호출 (callStack 생성)
   • 이미 방문한 Node는 함수 호출 X
   • 이 과정을 반복

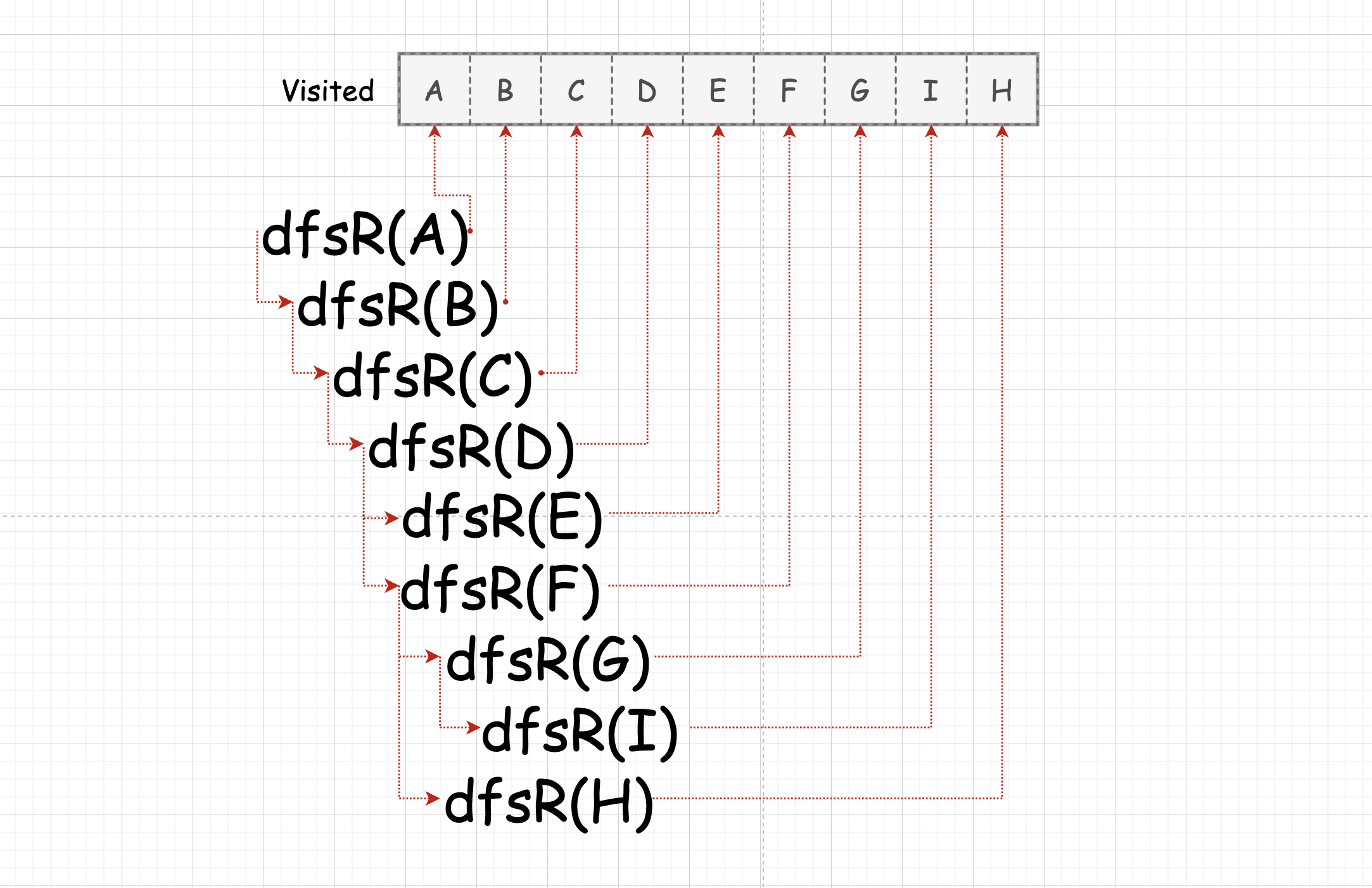
구현 코드

BFS (Breadth-First-Search)

• 루트 노드에서 시작해 인접한 노드를 먼저 탐색
• 시작지점에서 점차 범위를 넓혀가면서 탐색
• Queue를 사용

시간복잡도

인접 리스트

• V(정점 수) E(간선 수)
• 모든 정점들을 한 번씩 방문, 모든 간선을 한번씩 모두 체크했다고 가정 시
• O(V + E)

BFS 탐색 진행 방식 간단 예시

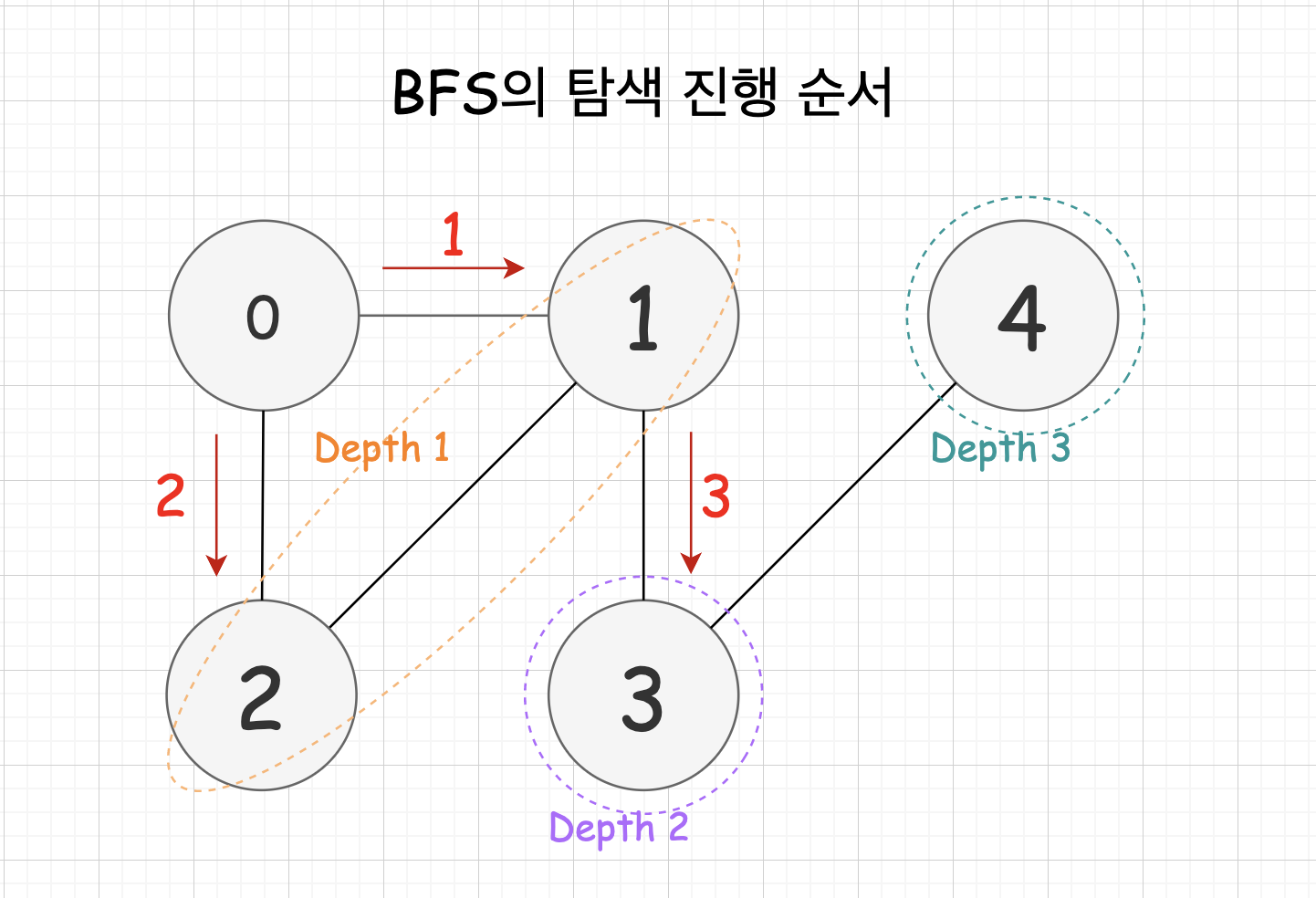
• 인접한 노드들을 전부 탐색하고 다음 depth로 넘어간다. 0 > 1 > 2 > 3 > 4

BFS 장단점

장점

• 최선의 경우, 가장 빠른 알고리즘이다. 운 좋게 한 번에 올바른 경로를 선택한다면, 최소 실행 시간에 정답을 찾을 수 있다.
• 찾으려는 노드의 depth가 깊다면, BFS보다 빠르게 찾을 수도 있다.

단점

• 경로가 매우 길 경우에는 탐색 가지가 급격히 증가함에 따라 보다 많은 기억 공간이 필요하다.
• 특정 분기만 지나치게 Depth가 깊다면, 효율이 굉장히 안좋을 수 있다.
  • 정답이 바로 앞에 있는데 뺑 돌아가는 경우가 있을 수 있다.
• 재귀 함수를 이용할 경우
  • 재귀가 깊어지면 메모리 비용을 예측하기 어렵다.
• 찾은 경로가 최단 경로라는 보장이 없다.

BFS - Iteration (Queue)

그래프 구조

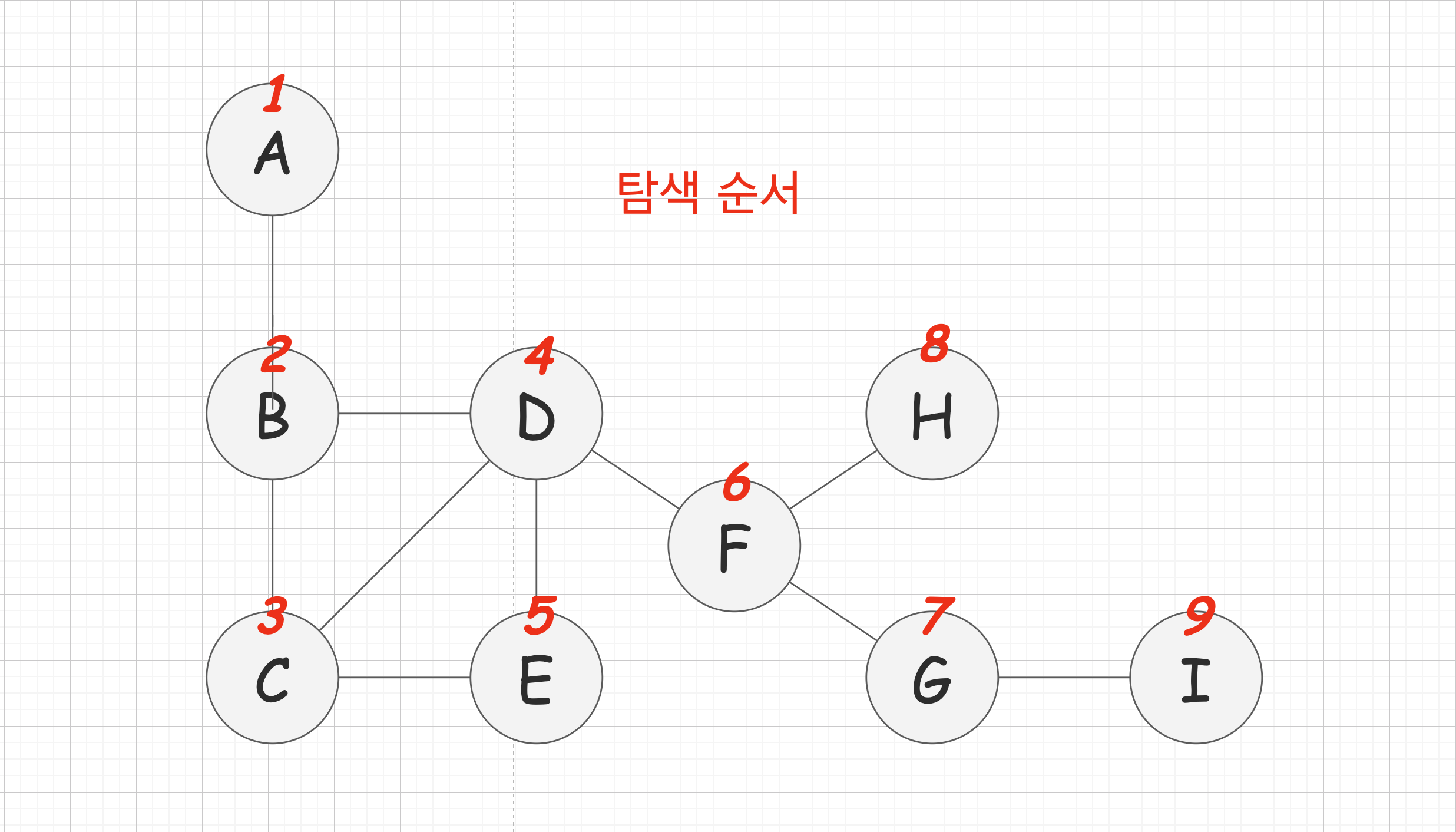
탐색 과정

• 시작 노드를 큐에 넣음
• 큐에서 하나를 꺼냄
• 꺼낸 노드에서 연결된 노드들을 전부 큐에 넣음
  • 이미 방문한 노드는 큐에 넣지 않음
• 꺼낸 노드를 출력
• 이 과정을 반복

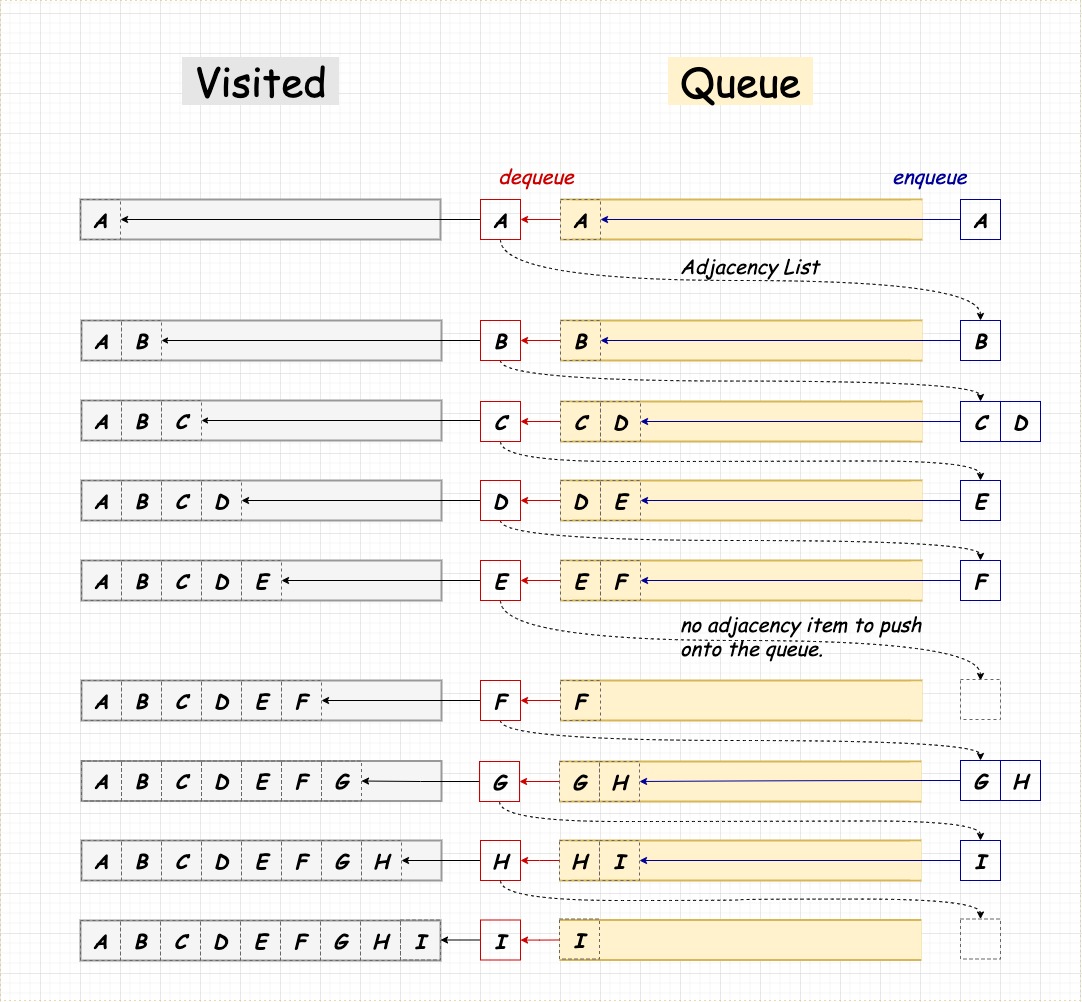
구현 코드

Reference

10분 테코톡 - 📚카프카의 탐색 알고리즘
Tree Traversals (Inorder, Preorder and Postorder)
Difference between BFS and DFS