
Binary Search (이진탐색)

- 시간복잡도
O(log N) - 정렬된 컬렉션에서 특정 값을 검색하는 프로세스
- 자바스크립트 배열로 구현할 수 있다.
- 상당히 빠르고 거대한 배열을 다룰 때 효과적이다.
- 길이가 10,000인 배열의 선형탐색 시간은 최악의 경우 10,000번
- 이진탐색은 최악의 경우 14번
- 컬렉션에서 인덱스 또는 요소를 검색해야 할 때 고려해야 한다.
- Binary Search는 검색 공간의 왼쪽, 오른쪽, 중간 인덱스를 유지하고 검색 대상을 비교하거나 컬렉션의 중간 값에 검색 조건을 적용
- 조건이 충족되지 않거나 값이 같지 않으면 검색 공간의 절반을 제거하고 성공할 때까지 나머지 절반에서 검색을 계속 진행
- 검색이 빈 반으로 끝나는 경우(더 이상 검색을 진행할 수 없는 경우)는 조건을 충족하는 값이 없음을 의미
이진탐색을 사용할 때 주의할 점
- Pre-processing - Sort if collection is unsorted.
- Binary Search - Using a loop or recursion to divide search space in half after each comparison.
- Post-processing - Determine viable candidates in the remaining space.
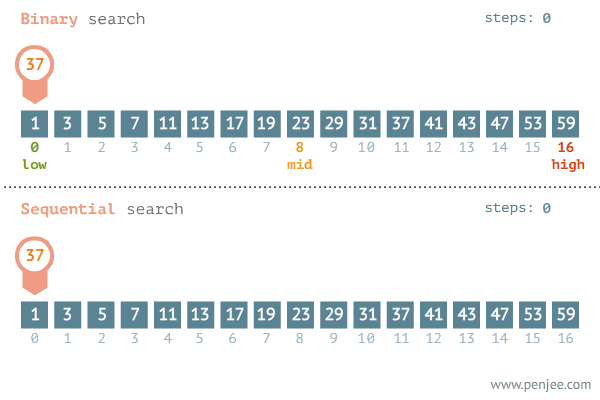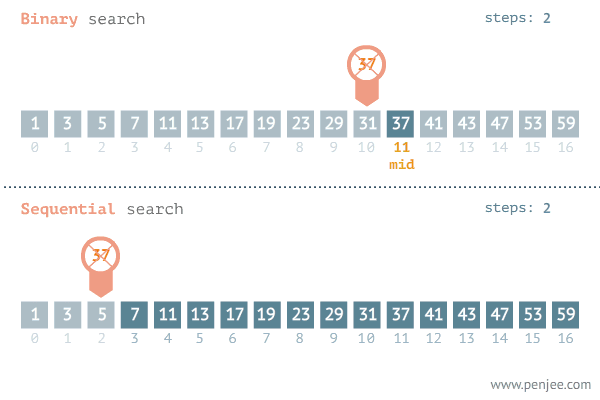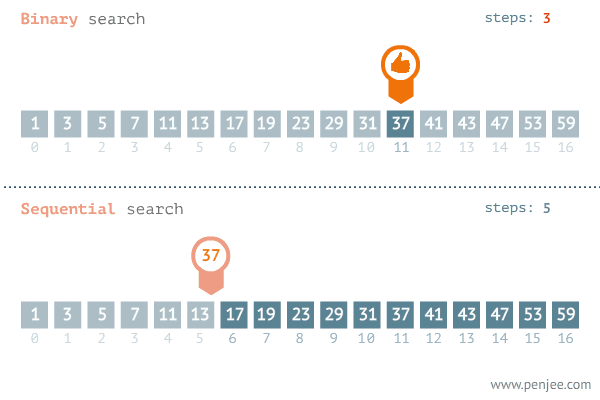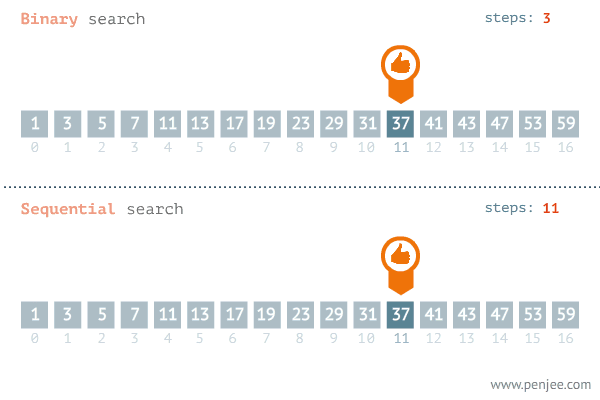
이진탐색 동작 예시
정렬된 배열에서 37 값을 찾는 과정 비교 선형탐색 vs 이진탐색
정렬된 배열에서 이진탐색으로 24를 탐색
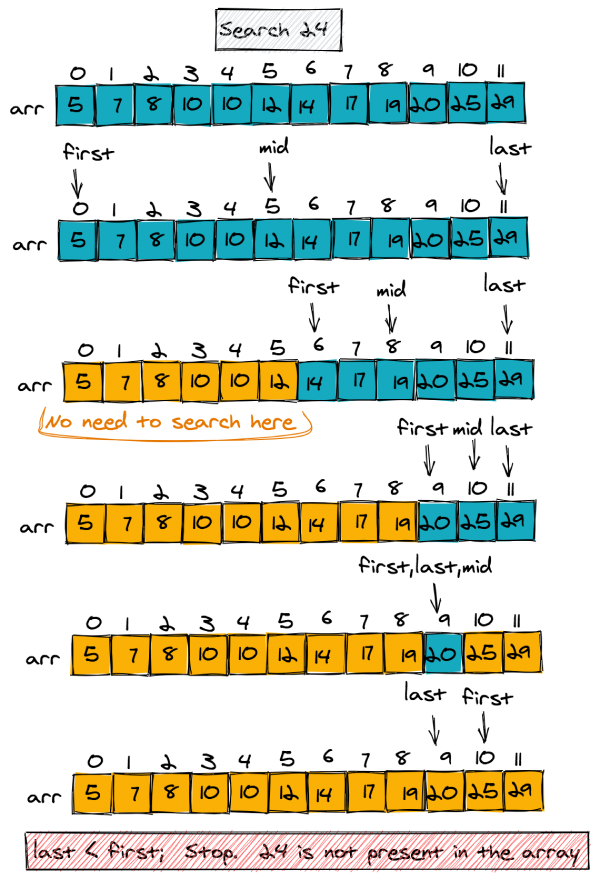
문제풀이
1. LeetCode - Binary Search
- 정렬된 정수 배열에서 일치하는 값을 찾는 가장 기본적인 이분탐색을 작성하는 문제다.
- 중간 값과
target을 비교하면서 이분탐색을 진행하면 된다.
/*
## Pseudo Code ##
1. 배열의 중간 값과 target을 비교 (이진탐색)
ㄴ start, mid, end index 값 변수 설정
2. while 반복문
ㄴ start 가 mid 같거나 보다 작을 때만 반복문 실행 (같거나는 nums의 길이가 1,2일 때)
ㄴ 1. mid value가 target과 같으면 => mid 리턴
ㄴ 2.
ㄴ mid value값이 target보다 크면 => end를 mid - 1로 변경 (앞쪽에서 찾자)
ㄴ mid value값이 target보다 작으면 => start를 mid + 1로 변경 (뒷쪽에서 찾자)
ㄴ 새로운 mid 구하기
*/
var search = function (nums, target) {
const getMid = (start, end) => Math.floor((start + end) / 2);
let start = 0;
let end = nums.length - 1;
let mid = getMid(start, end);
while (start <= end) {
const value = nums[mid];
if (value === target) {
return mid;
}
if (value > target) {
end = mid - 1;
} else {
start = mid + 1;
}
mid = getMid(start, end);
}
return -1;
};
2. LeetCode - Sqrt(x)
- 위의 1번 예시와 동일한 문제
- 검색 조건이
일치하는 값=>제곱근 여부로 변경
/*
## Pseudo Code ##
ㄴ 이진탐색으로 중간 값이 제곱근이 되는지 비교한다.
ㄴ 제곱근이거나 가장 가까운 낮은 정수를 리턴해야함
0. 예외 처리 : x가 0 또는 1일 경우 x를 리턴
1. 변수 설정
ㄴ low : 1 (최소값 - 2, 3 일 경우 1이 정답)
ㄴ high : x - 1 (최대값 - x가 x의 제곱근이 될 수 없음)
ㄴ candidate : low와 high의 중간 정수 값
2. while 반복문
ㄴ low 가 high와 같거나 작을 때만 반복문 실행
ㄴ 1. candidate * candidate가 x와 같으면 candidate 리턴
ㄴ 2.
ㄴ candidate * candidate가 x보다 크면 => high를 candidate - 1로 변경 (앞쪽에서 찾자)
ㄴ candidate * candidate가 x보다 작으면 => low를 candidate + 1로 변경 (뒷쪽에서 찾자)
ㄴ 새로운 candidate 구하기
3. 반복문이 다 돌고 종료됬으면 candidate 리턴
*/
var mySqrt = function (x) {
if (x === 0 || x === 1) return x;
let low = 1;
let high = x - 1;
let candidate = Math.floor((low + high) / 2);
while (low <= high) {
const square = candidate * candidate;
if (square === x) return candidate;
if (square > x) {
high = candidate - 1;
} else {
low = candidate + 1;
}
candidate = Math.floor((low + high) / 2);
}
return candidate;
};3. 프로그래머스 - 입국심사
https://school.programmers.co.kr/learn/courses/30/lessons/43238
- 문제 설명만 읽고는 이분탐색을 생각하지 못했지만 제한사항에 시간 범위가
1 ~ 1,000,000,000인 것을 확인하고 이진탐색을 생각했다. - 기본적인 로직은 간단한데, 검색 조건이 나에게 조금 까다로웠다.
- 주의했던 부분
- 처리가능한 사람 수와 실제 사람 수가 일치하더라도 시간이 차이가 날 수 있다.
/*
## Pseudo Code ##
- 이진탐색으로 구해보자.
- 모든 사람이 심사를 받는데 걸리는 예상최소시간 & 최대시간을 구하고 중간값부터 이진탐색으로 찾는다.
- 중간값(시간)이 소요됐을 때 처리가능한 사람 수를 구해서 그 실제 사람수보다
ㄴ 많으면 더 적은 시간으로 처리할 수 있는 것 : 중간값이 더 작아야함
ㄴ 적으면 더 많은 시간으로 처리할 수 있는 것 : 중간값이 더 커야함
- 이진탐색으로 전체를 돌고 나온 최소시간을 리턴
ㄴ 중간에 찾았다고 바로 리턴하면 안된다. 처리가능한 사람 수와 실제 사람 수가 일치하더라도 시간이 차이가 날 수 있음
1. 모든 사람이 심사를 받는데 걸리는 임의의 최소 시간, 최대 시간, 후보 시간 구하기
ㄴ fastest : 1 (제한 사항에 n 최소 1명, 심사관 최소 1, 걸리는 시간 최소 1)
ㄴ slowest : times 중 가장 높은 시간 * n (가장 오래걸리는 심사관한테 전부 받는 경우)
ㄴ candidate : fastest와 slowest 사이의 정수인 중간 값
2. while 반복문
ㄴ 조건 : fastest <= slowest
ㄴ candidate로 심사받을 수 있는 사람 수 judged 구하기
ㄴ judged와 n을 비교
ㄴ judged가 n보다 크면 => 더 적은 시간으로 처리가능하니까 slowest = candidate - 1
ㄴ judged가 n보다 작거나 같으면 => 더 많은 시간이 필요하니까 fastest = candidate + 1
3. candidate 리턴
*/
function solution(n, times) {
let fastest = Math.min(...times) * 1;
let slowest = Math.max(...times) * n;
let candidate = Math.floor((fastest + slowest) / 2);
while (fastest <= slowest) {
const judged = times.reduce((sum, time) => sum + Math.floor(candidate / time), 0);
if (judged < n) {
fastest = candidate + 1;
} else {
slowest = candidate - 1;
}
candidate = Math.floor((fastest + slowest) / 2);
}
return fastest;
}Reference
https://leetcode.com/explore/learn/card/binary-search/
https://leetcode.com/problems/binary-search/
https://leetcode.com/problems/sqrtx/
https://school.programmers.co.kr/learn/courses/30/lessons/43238
