💡 트리 (Tree)
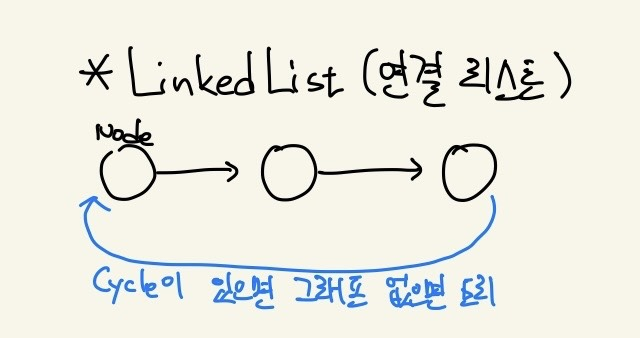
👉 노드와 링크로 구성된 자료구조 (그래프의 일종, Cycle 없음)
- 연결 리스트도 트리의 일종
👉 계층적 구조를 나타낼 때 사용하는 자료구조
- 폴더 구조 (디렉토리, 서브 디렉토리)
- ex. 조직도, 가계도 등
💡 트리의 구조
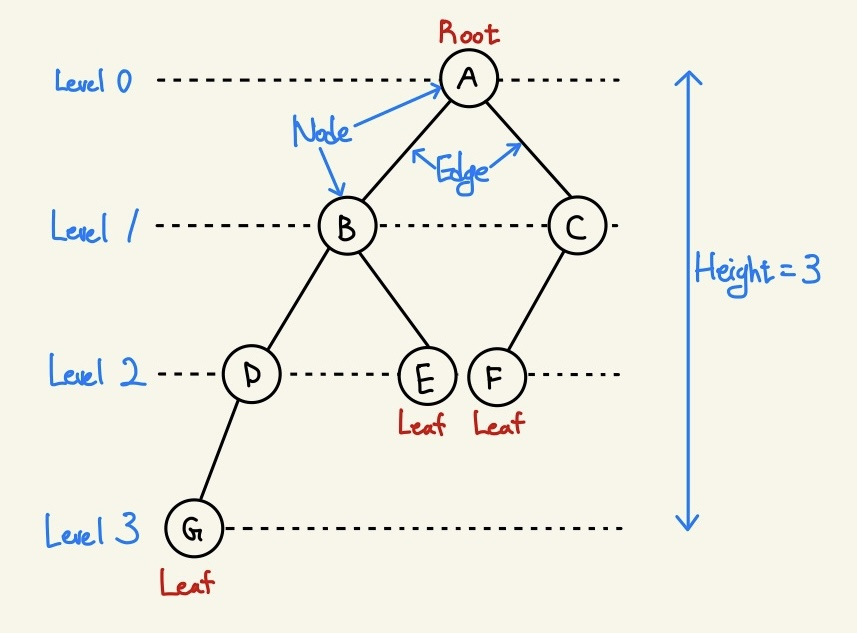
👉 노드 (Node) : 트리 구조의 자료 값을 담고 있는 단위
👉 에지 (Edge) : 노드 간의 연결선 (=link, branch)
👉 루트 노드 (Root) : 부모가 없는 노드, 최상단 노드
👉 잎새 노드 (Leaf) : 자식이 없는 노드 (=단말)
👉 내부 노드 (Internal) : 잎새 노드를 제외한 모든 노드
👉 부모 (Parent) : 연결된 두 노드 중 상위의 노드
👉 자식 (Child) : 연결된 두 노드 중 하위의 노드
👉 형제 (Sibling) : 같은 부모를 가지는 노드
👉 깊이 (Depth) : 루트에서 어떤 노드까지의 간선의 수
👉 레벨 (Level) : 트리의 특정 깊이를 가지는 노드 집합
👉 높이 (Height) : 트리에서 가장 큰 레벨 값
👉 크기 (Size) : 자신을 포함한 자식 노드의 개수
👉 차수 (Degree) : 각 노드가 지닌 가지의 수
👉 트리의 차수 : 트리의 최대 차수
💡 트리의 특징
👉 하나의 노드에서 다른 노드로 이동하는 경로는 유일하다.
👉 노드가 N개인 트리의 Edge의 수는 N-1개이다.
👉 Acyclic : Cycle이 존재하지 않는다.
👉 모든 노드는 서로 연결되어 있다.
👉 하나의 Edge를 끊으면 2개의 Sub-Tree 로 분리된다.
💡 이진 트리 (Binary Tree)
👉 각 노드는 최대 2개의 자식을 가질 수 있다.
👉 자식 노드는 좌우를 구분한다.
- 왼쪽 자식 : 부모 노드의 왼쪽 아래
- 오른쪽 자식 : 부모 노드의 오른쪽 아래
💡 이진 트리의 종류
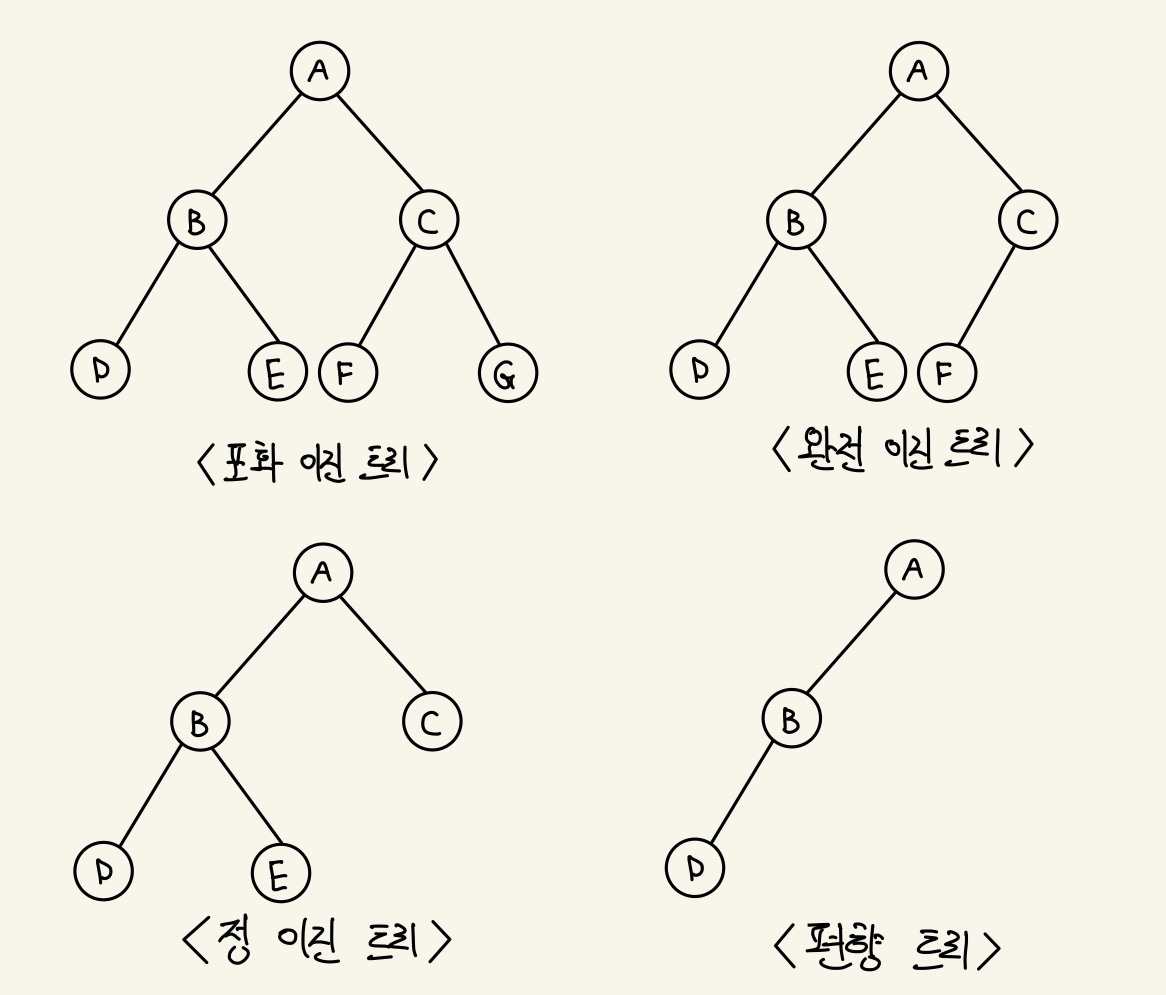
👉 포화 이진 트리 (Perfect Binary Tree)
- 모든 레벨에서 노드들이 꽉 채워져 있는 트리
👉 완전 이진 트리 (Complete Binary Tree)
- 마지막 레벨을 제외하고 노드들이 모두 채워져 있는 트리
👉 정 이진 트리 (Full Binary Tree)
- 모든 노드가 0개 또는 2개의 자식 노드를 갖는 트리
👉 편향 트리 (Skewed Binary Tree) (사향 트리)
- 한쪽으로 기울어진 트리
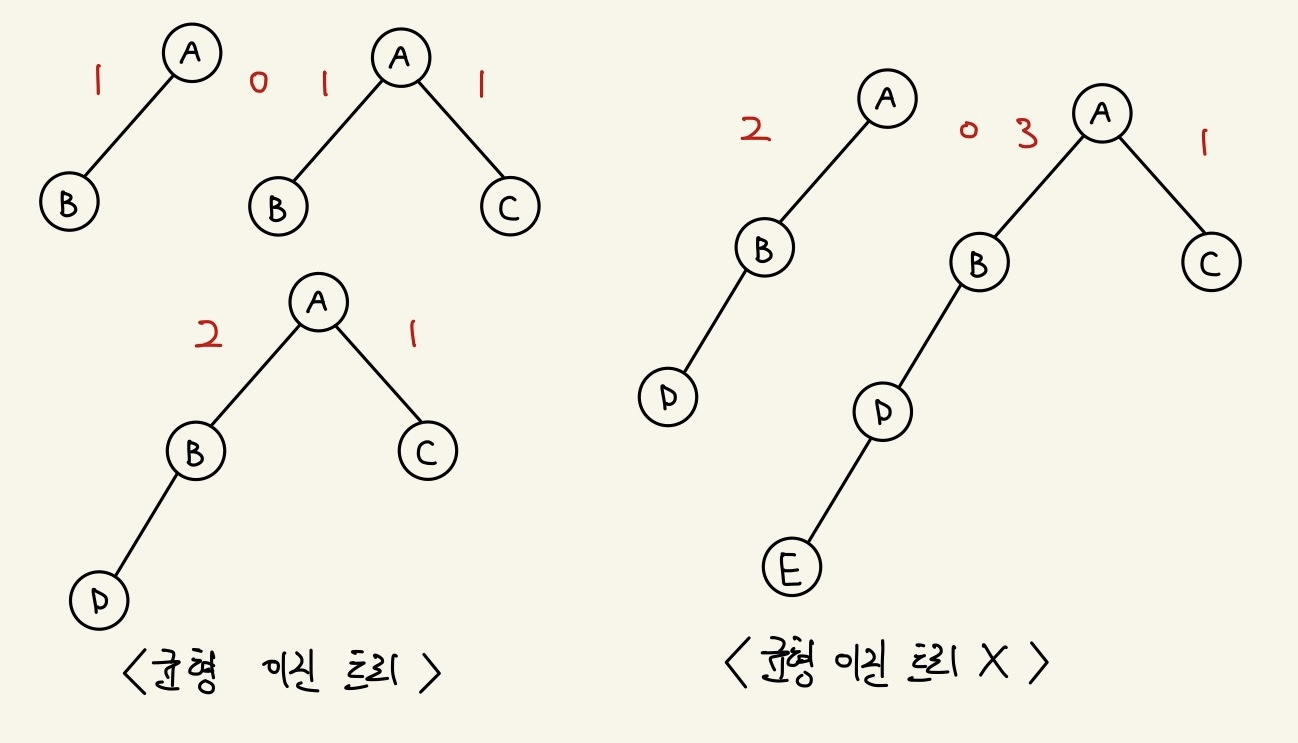
👉 균형 이진 트리 (Balanced Binary Tree)
- 모든 노드의 좌우 서브 트리 높이가 1 이상 차이가 나지 않는 트리
💡 이진 트리의 특징
👉 포화 이진 트리의 높이가 h 일때, 노드의 수는 2ʰ⁺¹ - 1개
👉 포화 or 완전 이진 트리의 노드가 N 개 일 때, 높이는 logN
👉 이진 트리의 노드가 N 개 일 때, 최대 가능 높이는 N - 1
💡 이진 트리의 순회 (Traversal)
👉 모든 노드를 빠뜨리거나 중복하지 않고 방문하는 연산
👉 순회 종류
- DFS (Depth First Search) : 전위 순회, 중위 순회, 후위 순회
- BFS (Breadth First Search) : 레벨 순회
💡 이진 트리의 순회 - 전위 순회
👉 Preorder Traversal
👉 방문 순서 : 현재 노드 → 왼쪽 노드 → 오른쪽 노드
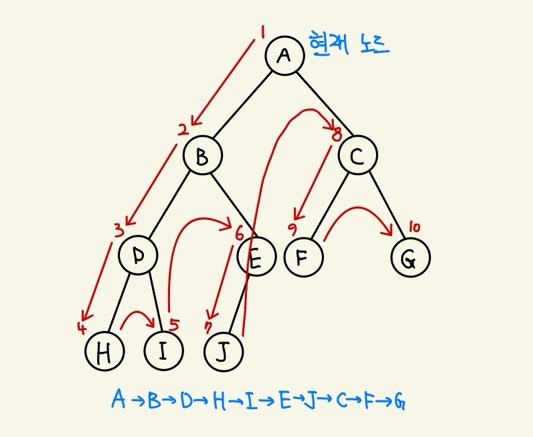
💡 이진 트리의 순회 - 중위 순회
👉 Inorder Traversal
👉 방문 순서 : 왼쪽 노드 → 현재 노드 → 오른쪽 노드
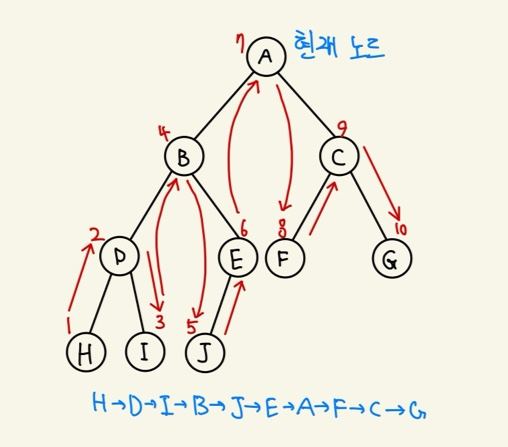
💡 이진 트리의 순회 - 후위 순회
👉 Postorder Traversal
👉 방문 순서 : 왼쪽 노드 → 오른쪽 노드 → 현재 노드
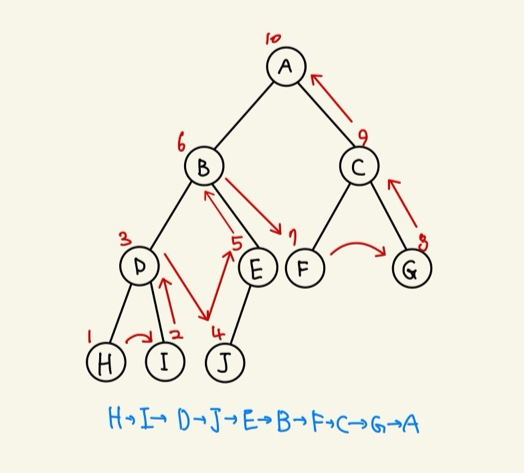
💡 이진 트리의 순회 - 레벨 순회
👉 Levelorder Traversal
👉 방문 순서 : 위쪽 레벨부터 왼쪽 노드 → 오른쪽 노드
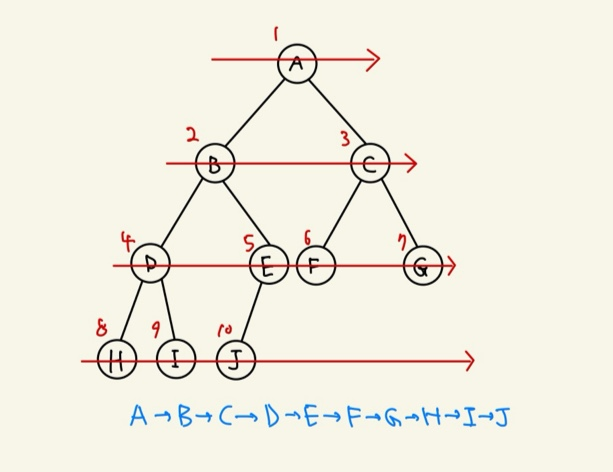
💡 이진 트리의 구현
👉 배열
- 레벨 순회 순으로 배열에 구성
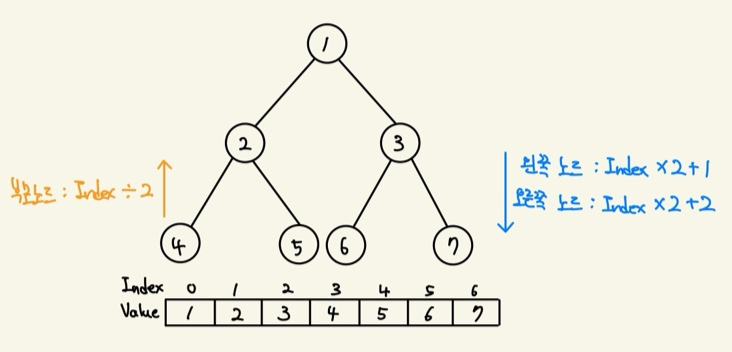
👉 연결 리스트
- 값과 간선을 관리하기 위한 노드로 연결리스트 구성
BE