백준 11052: 카드 구매하기(C++)

생각 흐름

이런 식으로 하나하나 따져 봐야 하면서, 지금의 선택이 이전의 선택에 영향을 받는 류의 문제는 점화식을 세워서 푼다.
N개를 갖기 위해 지불해야 하는 금액의 최댓값을 f(N)이라고 보면,

f(N)= P1          (if N=1)
	= Pk+f(N-k)   (if N!=1) (1<=k<=N)

이라고 볼 수 있다.
( f(1), f(2), f(3) 등을 차례대로 구해 보면 저 공식이 자연스럽게 떠오를 것이다.)

지금의 선택값이 이전의 선택값에 영향을 받으므로 recursion을 활용하면 될 것이다.
결국 모든 것이 base condition으로 수렴할 텐데, base condition은 P1(if N=1)이다.

그런데 recursion의 경우 모든 걸 하나하나 따져 볼 때 시간과 메모리가 많이 들어간다.
f(N)을 구하려면 최대값인지를 알기 위해 모든 경우의 수를 base condition으로 수렴할 때까지 따져 볼 텐데, 거기서 다른 경우의 수에서 구해 놓은 값을 또 계산하는 경우가 많이 발생한다.

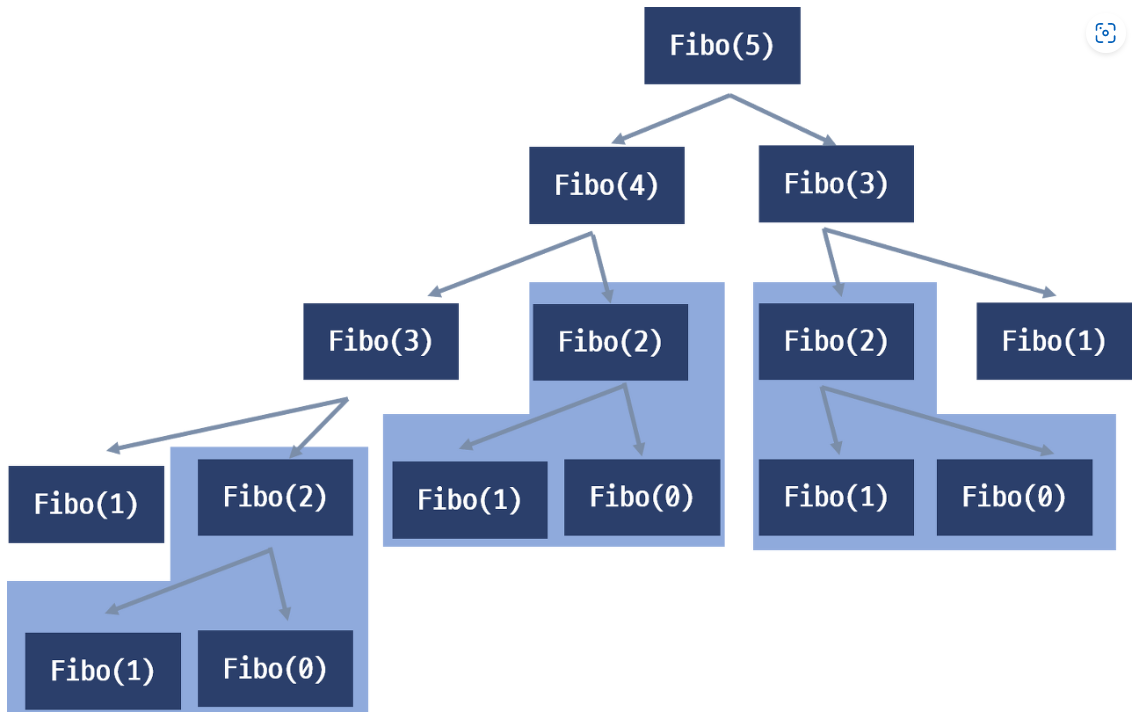
(위는 fibonacci 수열에 대한 예시이다. base condition인 모든 가지가 fibo(0)과 Fibo(1)까지 가기 위해 중간에 중복되는 값들을 계속 구하는 것을 볼 수 있다.)

따라서 어떤 f(k)값을 구한 다음 다른 배열에 저장을 해 놓는 과정이 필요하다.

코드

#include<iostream>
#include<vector>

using namespace std;

int record[1001] = {0,};
int maxn = 0;

int calc(int N, vector<int> p_i) {
    if (N == 0) { return 0; } //base condition: f(0)
    if (N == 1) { return p_i[1]; } //base condition: p_1

    for (int i = 1; i <= N; i++) {
        if (record[N - i] == 0) {
            record[N - i] = calc(N - i, p_i); //recursion
        }
        maxn = (maxn > p_i[i] + record[N - i]) ? maxn : p_i[i] + record[N - i];
    }
    return maxn;
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(NULL); cout.tie(NULL);

    int N; cin >> N;
    vector<int> p_i(N + 1);
    for (int i = 1; i <= N; i++) { //index==i 되도록, p_0이 0이도록
        cin >> p_i[i];
    }

    cout << calc(N, p_i);

    return 0;
}