[CS/알고리즘] 누적합과 차분배열

황제연·2025년 3월 24일

CS 누적합 알고리즘 차분배열

CS학습

목록 보기

23/193

🔍누적합 (Prefix Sum)

누적합은 주어진 배열의 각 원소까지의 합을 미리 계산하여 저장하는 기법입니다
이를 통해 특정 구간의 합을 빠르게 구할 수 있습니다

📌 예시

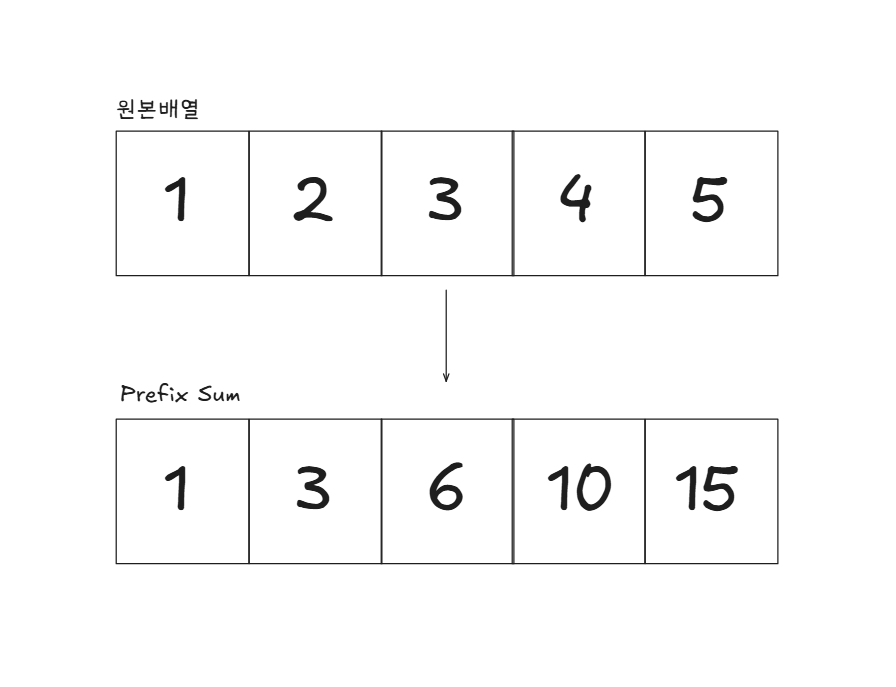
주어진 배열 arr 이 [1, 2, 3, 4, 5]라면, 각 원소까지의 누적합은 다음과 같이 계산됩니다

sum[0] = arr[0] = 1
sum[1] = sum[0] + arr[1] = 1 + 2 = 3
sum[2] = sum[1] + arr[2] = 3 + 3 = 6
sum[3] = sum[2] + arr[3] = 6 + 4 = 10
sum[4] = sum[3] + arr[4] = 10 + 5 = 15

따라서, 누적합 배열 sum은 [1, 3, 6, 10, 15]가 됩니다

📌 구간 합 계산

누적합 배열을 사용하면 배열 arr의 i번째 원소부터 j번째 원소까지의 합을
sum[j] - sum[i-1]로 O(1) 시간에 계산할 수 있습니다
단, i = 0인 경우에는 sum[j]가 해당 구간의 합이 됩니다

🔍차분 배열 (Difference Array)

차분 배열은 배열의 연속된 구간에 일정한 값을 더하거나 빼는 연산을 효율적으로 수행하기 위한 기법입니다
주어진 배열의 변화를 저장하는 차분배열을 생성하여, 여러 구간에 대한 업데이트를 빠르게 처리할 수 있습니다

📌 예시

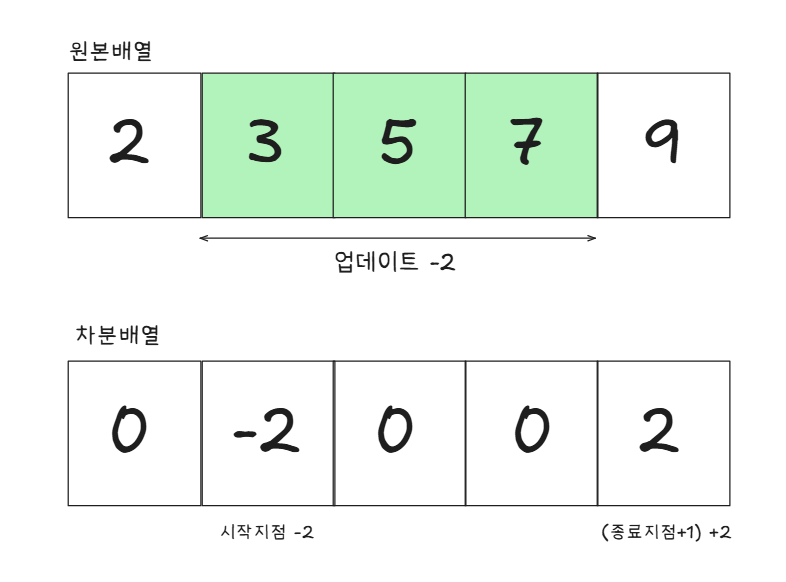
초기 배열 arr이 [2, 3, 5, 7, 11]일 때, 1~3 범위를 -2만큼 업데이트한다면
차분배열 diff는 다음과 같이 계산됩니다

diff[0] = 0
diff[1] = -2
diff[2] = 0
diff[3] = 0
diff[4] = 2

업데이트의 시작지점과 (종료지점 + 1)에만 업데이트 수치를 적용합니다
결과적으로 차분 배열 diff는 [0, -2, 0, 0, 2]가 됩니다

📌 구간 업데이트

배열 arr의 i번째 원소부터 j번째 원소까지 k를 더하고자 할 때, 다음과 같이 구현할 수 있습니다

diff[i] += k
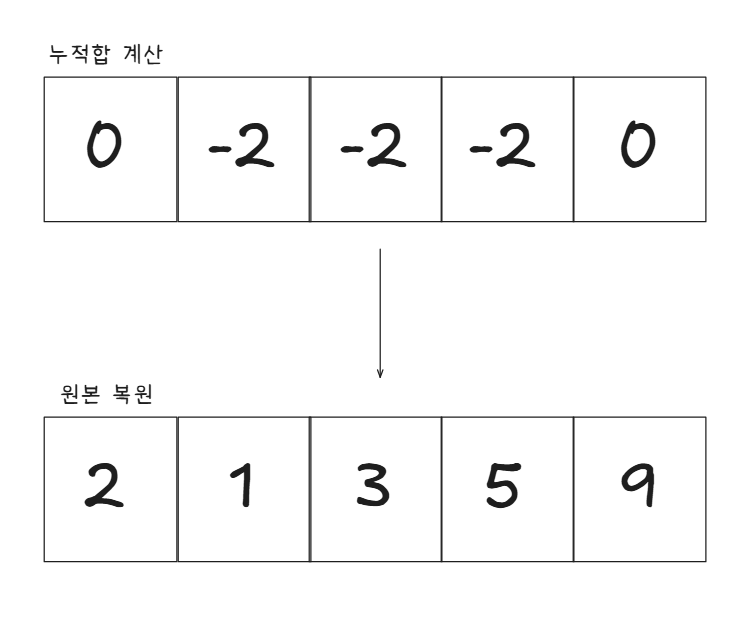
diff[j+1] -= k

이러한 업데이트를 수행한 후, 차분 배열 diff를 기반으로 원본 배열 arr를 복원하려면
다시 누적합을 계산하고 원본배열의 값과 합산하면 됩니다

🚀누적합과 차분배열이 적용된 문제

백준 19951번 - 태상이의 훈련소 생활 문제는 누적합 및 차분 배열을 적용해 해결할 수 있는 대표적인 문제입니다

이 문제는 구간 업데이트를 여러 번 반복해야 하는 경우로, 브루트포스 방식으로 접근하면 시간 초과가 발생할 수 있습니다

따라서 다음과 같은 방식으로 차분 배열과 누적합을 이용해 해결할 수 있습니다

        int[] sum = new int[n+2]; // 누적합 배열
        for (int i = 0; i < m; i++) {
            sum[a] += val; // a: 시작지점
            sum[b+1] -= val; // b: 종료지점
        } // 차분배열 기법

        for (int i = 1; i < n+1; i++) {
           sum[i] = sum[i-1] + sum[i]; // 누적합 계산
        }
        for (int i = 1; i < n + 1; i++) {
            arr[i] = arr[i] + sum[i]; // 업데이트 결과 복원
        }