🔍선택 정렬 알고리즘이란?

선택 정렬(Selection Sort)은 배열의 처음부터 끝까지 순회하면서
가장 작은 값(혹은 큰 값)을 찾아 맨 앞으로 가져오는 정렬 알고리즘입니다

📌선택 정렬의 동작 방식

실제 예시를 통해 선택 정렬의 동작방식을 살펴보겠습니다
예를 들어, [7, 5, 3, 1] 배열을 오름차순으로 정렬할 것입니다

오름차순 정렬을 위해서는 가장 작은 값을 찾아야합니다
따라서 배열의 처음부터 끝까지 순회하며 가장 작은 값을 찾을 것입니다

🎈 1회차 비교 과정:

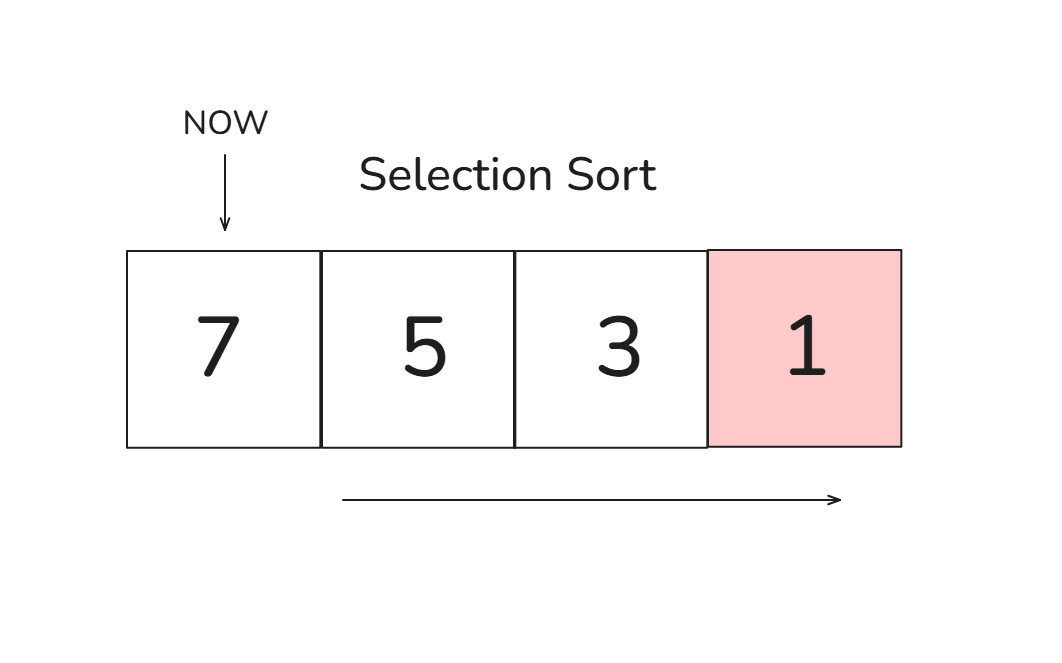
• 처음 위치(7)에서 [5, 3, 1] 중 가장 작은 값인 1을 찾고 7과 교환합니다 → [1, 5, 3, 7]

🎈 2회차 비교 과정:

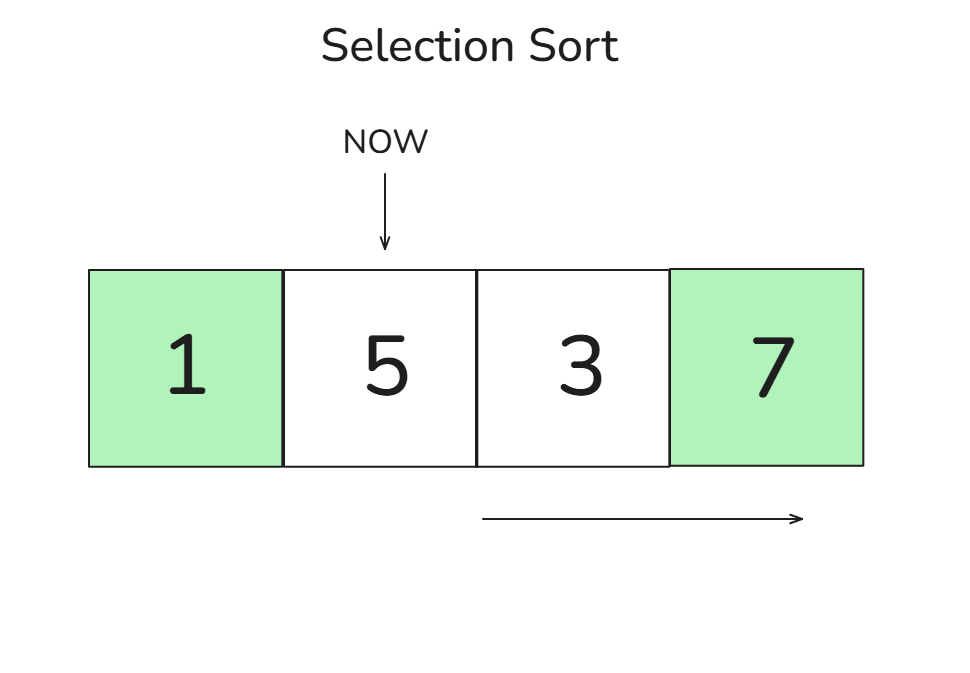
• 다음 위치(5)에서 [3, 7] 중 가장 작은 값인 3을 찾고 5와 교환합니다 → [1, 3, 5, 7]

🎈 3회차 비교 과정:

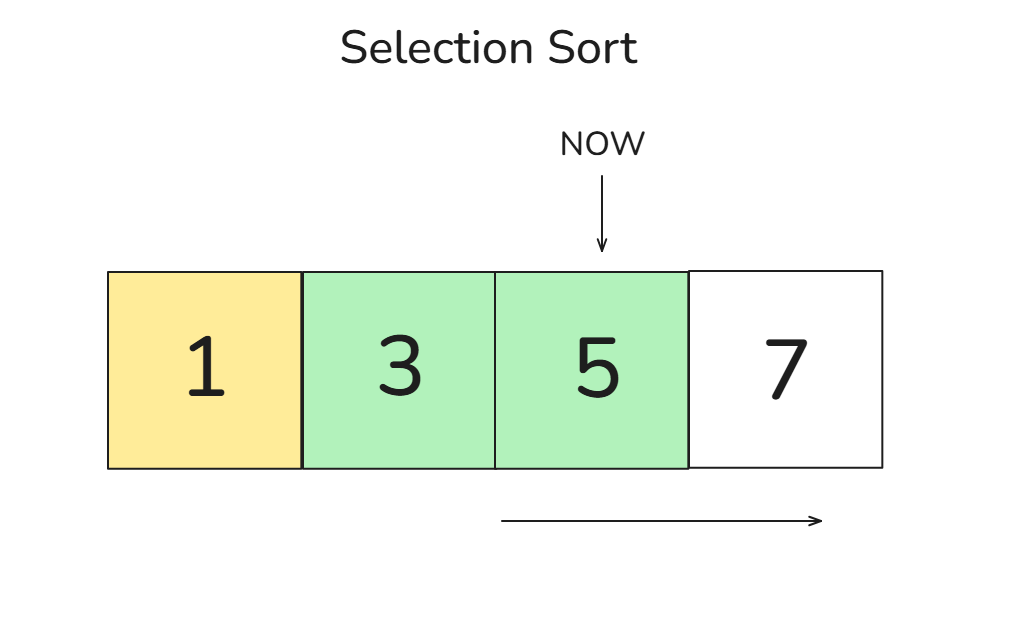
• 다음 위치(5)는 이미 가장 작은 값이라 그대로 둡니다 → [1, 3, 5, 7]

🎈 4회차 비교 과정:

• 마지막 위치는 비교할 필요가 없습니다

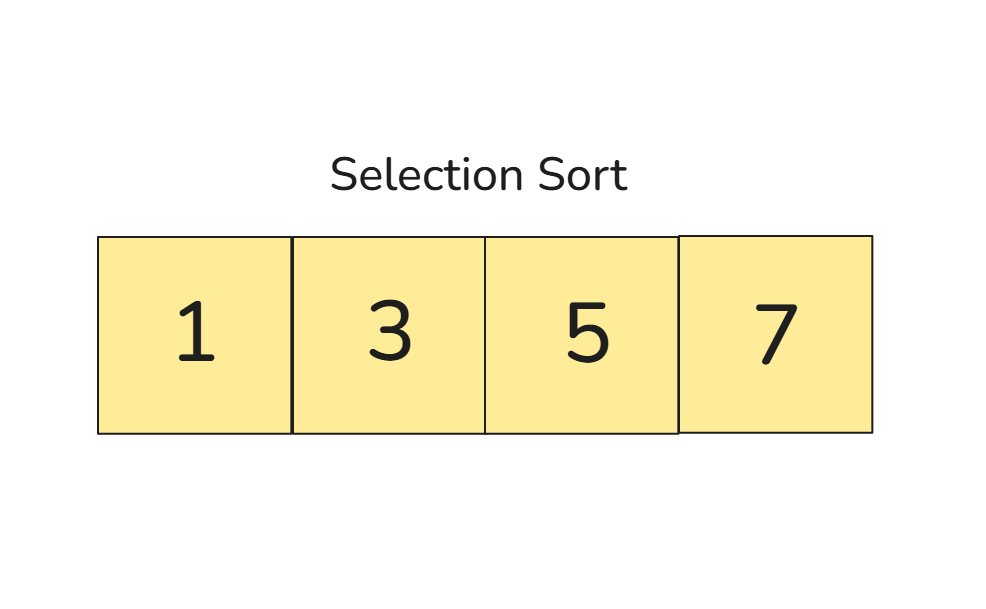
이제 모든 숫자가 오름차순으로 정렬되었습니다 ([1, 3, 5, 7])

🚀 실제 코드로 구현하기

위에서 설명한 동작 방식을 코드로 구현하면 다음과 같습니다

int[] arr = {7, 5, 3, 1};  
int n = arr.length;  
for (int i = 0; i < n-1; i++) {  
    int min = i;  
    for (int j = i+1; j < n; j++) {  
        if(arr[j] < arr[min]){  
            min = j;  
        }  
    }  
    int tmp = arr[min];  
    arr[min] = arr[i];  
    arr[i] = tmp;  
}

이 코드를 실행하면 배열은 [1, 3, 5, 7]의 형태로 오름차순 정렬됩니다

🛠️ 시간복잡도

선택 정렬은 모든 경우에 O(n²)의 시간 복잡도를 가집니다
따라서 배열의 크기가 커질수록 실행 시간이 증가합니다

• 최악의 경우 시간 복잡도: O(n²)
• 평균 시간 복잡도: O(n²)
• 최선의 경우 시간 복잡도: O(n²)

📌 장점

• 추가적인 공간을 사용하지 않고 기존 배열 내에서 정렬합니다. 따라서 메모리 효율적입니다 (In-place 정렬)

📌 단점

• 성능이 나쁩니다 (시간복잡도: O(n²))
• 안정 정렬(Stable Sort)이 아닙니다. 따라서 같은 값의 상대적인 순서가 보장되지 않습니다

✨선택정렬이 안정정렬이 아닌 이유

선택 정렬이 안정 정렬이 아닌 이유는
같은 값이 여러 개 있을 때, 원본 배열에서 먼저 있던 값이 뒤로 밀릴 수 있기 때문입니다

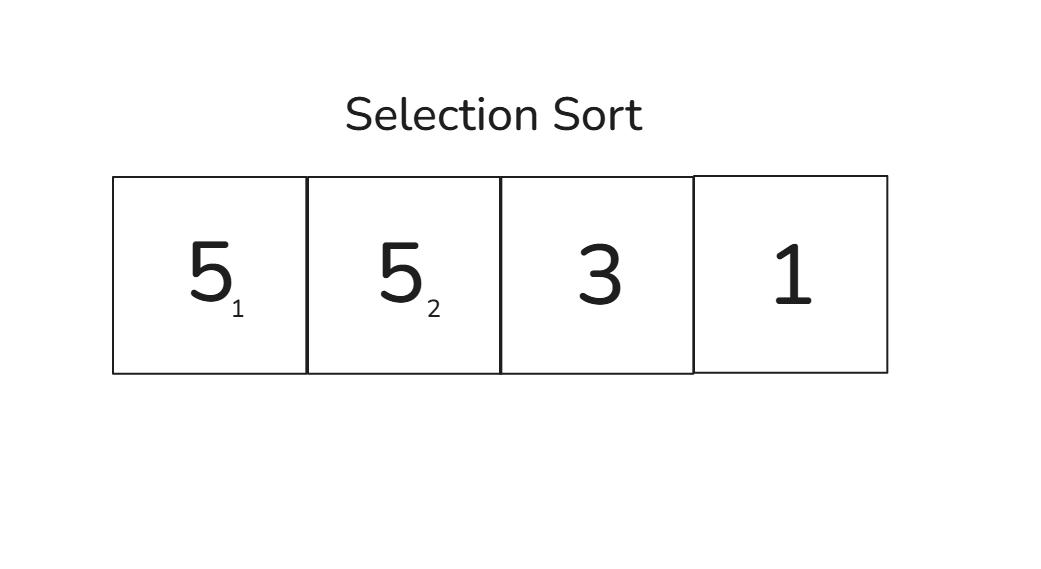
예를 들어 [5₁, 5₂, 3, 1] 배열을 오름차순으로 정렬할 것입니다
선택 정렬은 가장 작은 숫자를 찾아서 맨 앞으로 가져옵니다

• 첫 번째 선택으로 1과 5₁이 교환됩니다
  

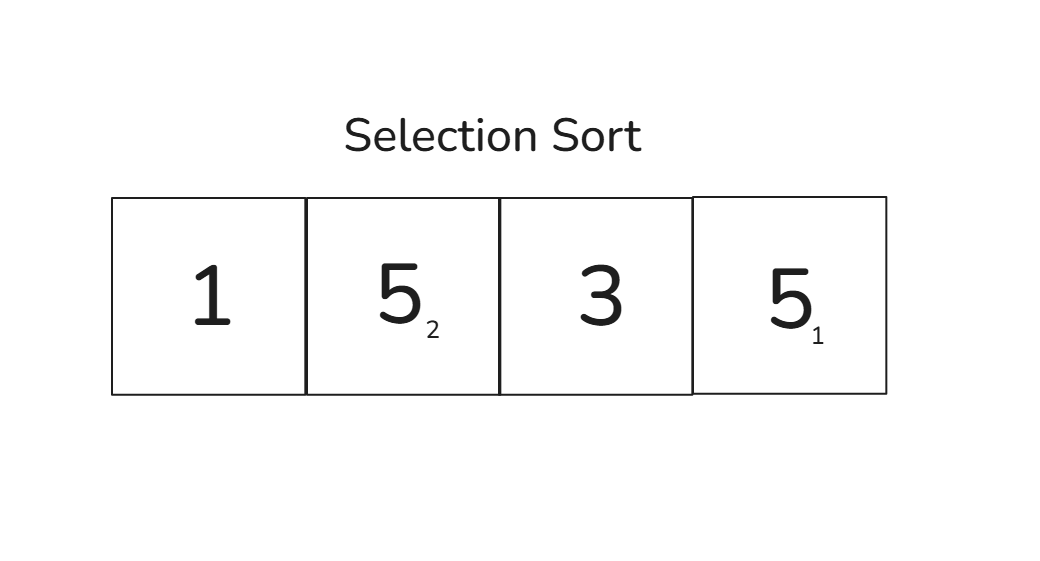
• 배열은 [1, 5₂, 3, 5₁]이 됩니다

여기서 문제는 처음에 있던 5₁이 뒤로 이동하면서, 나중에 있던 5₂보다 뒤로 가게 됩니다
즉, 같은 값의 원본 위치가 뒤바뀌었습니다
따라서 선택 정렬은 안정 정렬이 아닙니다

반면, 버블 정렬은 인접한 두 원소끼리만 비교해서 교환합니다
이 과정에서 같은 값끼리는 위치가 바뀌지 않기 때문에 안정 정렬입니다
예를 들어 위 배열을 버블 정렬로 하면,

• 처음 상태: [5₁, 5₂, 3, 1]
  

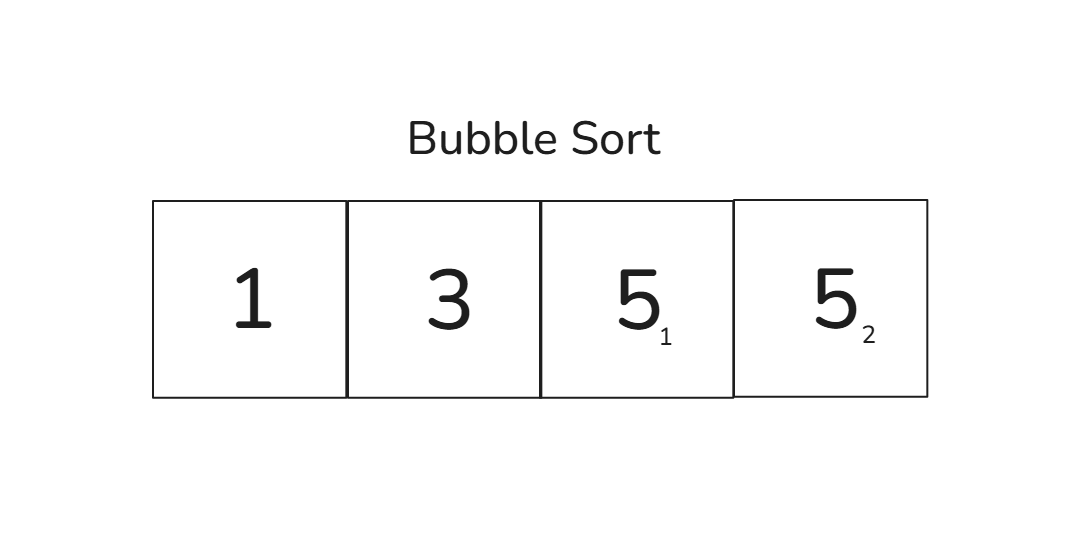
• 비교와 교환을 반복해도 5₁과 5₂의 순서는 유지됩니다
  따라서 같은 값의 상대적 위치가 보장됩니다

✍️ 결론

선택 정렬은 배열의 처음부터 끝까지 순회하면서
가장 작은 값(혹은 큰 값)을 찾아 맨 앞으로 가져오는 정렬 알고리즘입니다

별도의 추가 공간 없이 배열 내에서 정렬(In-place)이 가능하지만 안정정렬이 아니고
시간복잡도가 좋지 않다는 단점이 존재합니다