🔍 퀵정렬 알고리즘이란?

퀵정렬(Quick Sort)은 기준점(pivot)을 정해서 기준보다 작은 값과 큰 값을 분리하고,
다시 각각의 그룹에서 동일한 작업을 반복하는 방식으로 정렬하는 알고리즘입니다

📌 퀵정렬의 동작 방식

퀵정렬도 분할 정복(divide and conquer) 방식을 사용합니다

퀵정렬의 전체 흐름은 다음과 같습니다:

1. 맨 오른쪽 숫자를 피벗으로 선택합니다
2. 피벗을 기준으로 왼쪽에서부터 피벗보다 큰 수를 찾습니다
3. 오른쪽에서부터 피벗보다 작은 수를 찾습니다
4. 두 수를 찾았다면 위치를 서로 바꿔줍니다
5. 한쪽만 만족하거나 교차하면, 피벗과 현재 위치의 값을 교환합니다
6. 피벗의 위치를 기준으로 왼쪽과 오른쪽 그룹에 대해 같은 작업을 반복합니다

실제 예시를 통해 퀵정렬의 동작 방식을 살펴보겠습니다
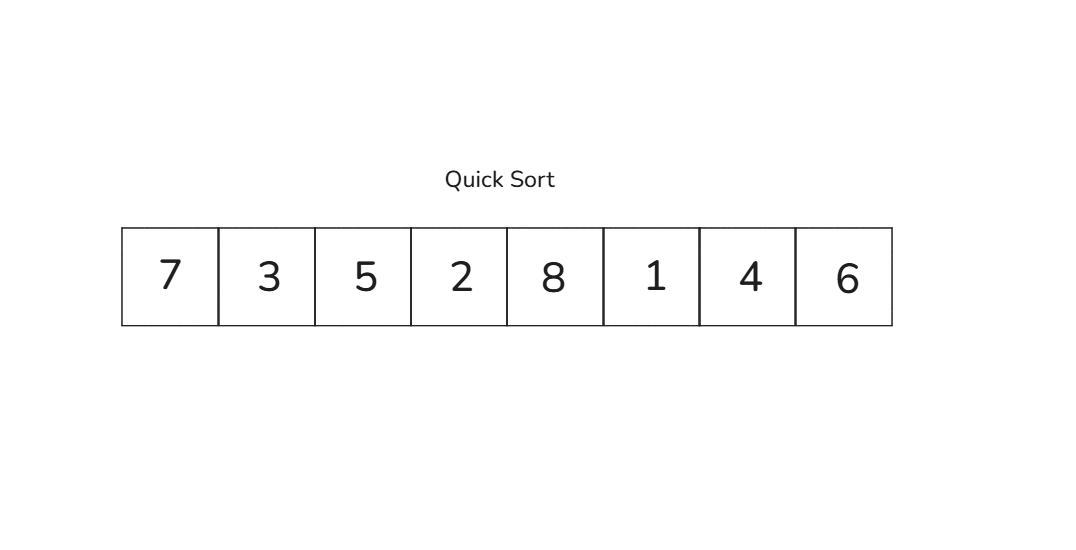
예를들어 [7, 3, 5, 2, 8, 1, 4, 6] 배열을 오름차순으로 정렬할 것입니다

🎈 회차별 비교 예시

🎈 1회차 비교 과정:

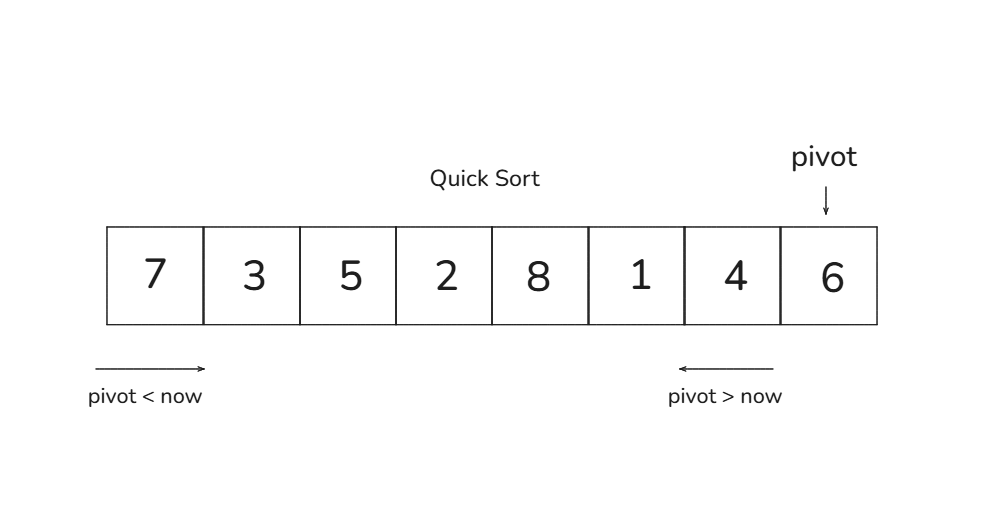
피벗으로 맨 뒤 숫자인 6을 선택합니다
1. 왼쪽에서부터 피벗보다 큰 수(7)를 찾습니다
2. 오른쪽에서부터 피벗보다 작은 수(4)를 찾습니다
3. 두 수를 교환합니다 → [4, 3, 5, 2, 8, 1, 7, 6]
4. 같은 과정을 반복하여 8과 1을 교환합니다 → [4, 3, 5, 2, 1, 8, 7, 6]
5. 왼쪽(8)과 오른쪽(1)이 교차했으므로 피벗(6)과 8을 교환합니다 → [4, 3, 5, 2, 1, 6, 7, 8]

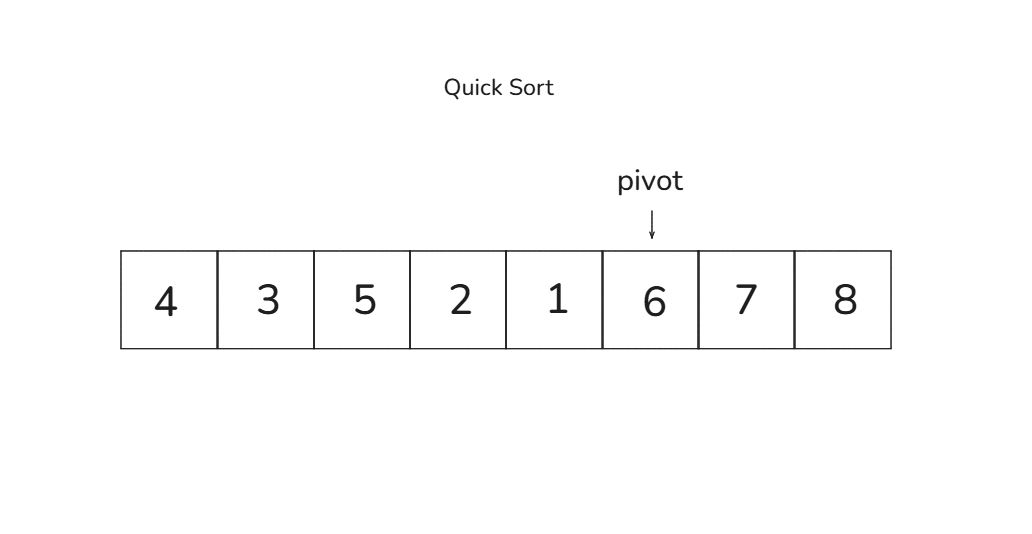
피벗 기준으로 왼쪽 그룹 [4, 3, 5, 2, 1]과 오른쪽 그룹 [7, 8]으로 나눴습니다

🎈 2회차 비교 과정 (왼쪽 그룹: [4, 3, 5, 2, 1]):

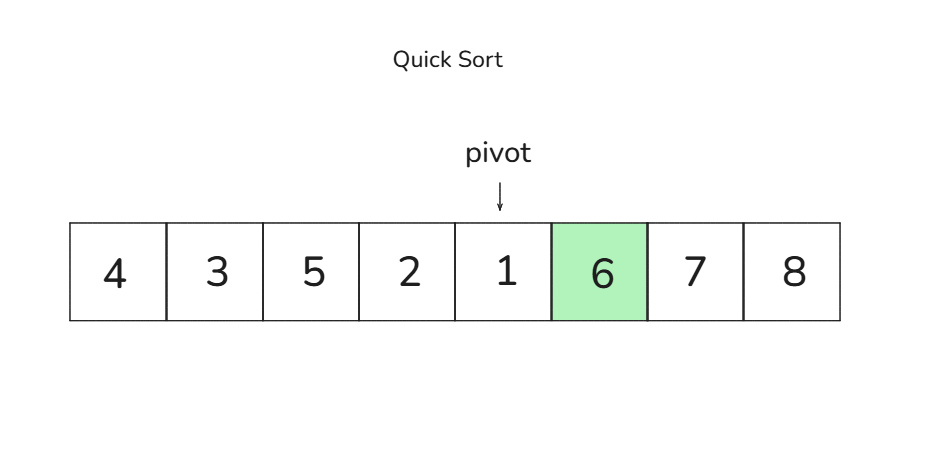
다음 피벗은 1입니다
1. 왼쪽부터 큰 값(4), 오른쪽부터 작은 값을 찾지만 작은 값이 없습니다
2. 피벗 1과 왼쪽 첫 수 4를 교환합니다 → [1, 3, 5, 2, 4]

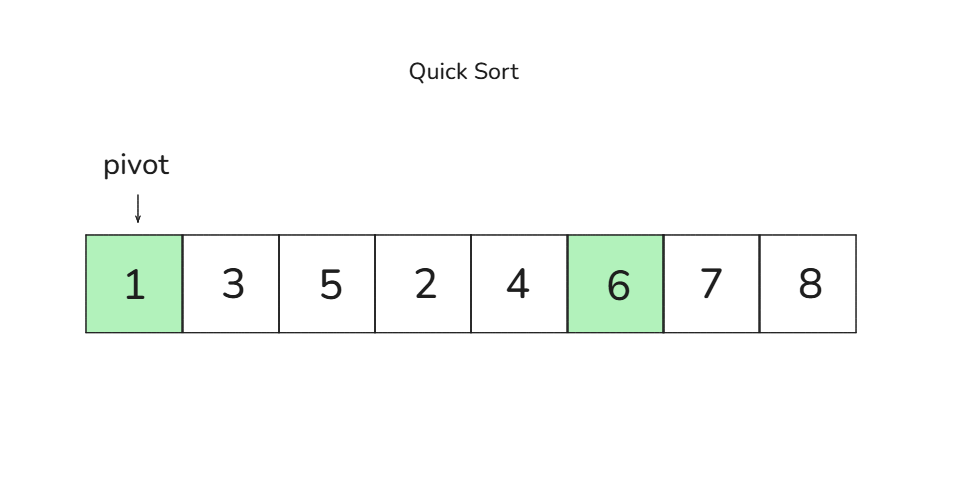
왼쪽에 해당하는 그룹이 없으므로 오른쪽 그룹만 확인하면 됩니다 [3, 5, 2, 4]

🎈 3회차 비교 과정 (오른쪽 그룹: [3, 5, 2, 4]):

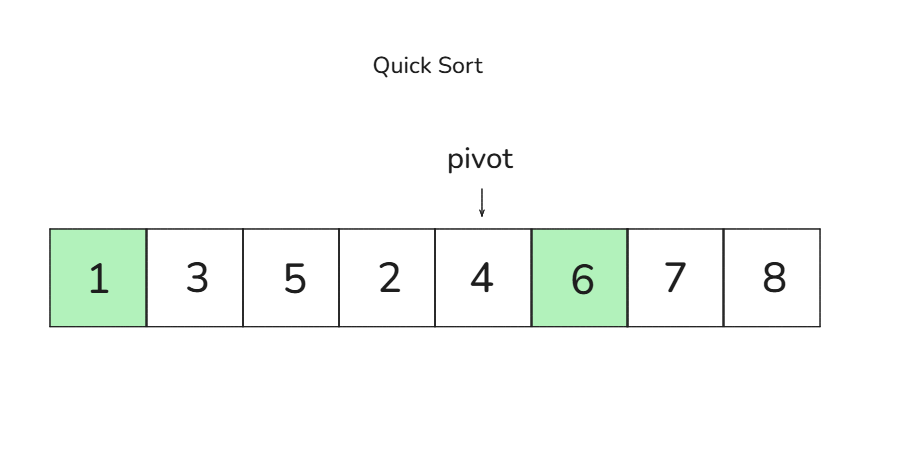
다음 피벗은 4입니다
1. 왼쪽부터 큰 값(5), 오른쪽부터 작은 값(2)을 찾아 교환합니다 → [3, 2, 5, 4]
2. 더 이상 교환할 값이 없으므로, 피벗 4와 큰 값 5를 교환합니다 → [3, 2, 4, 5]

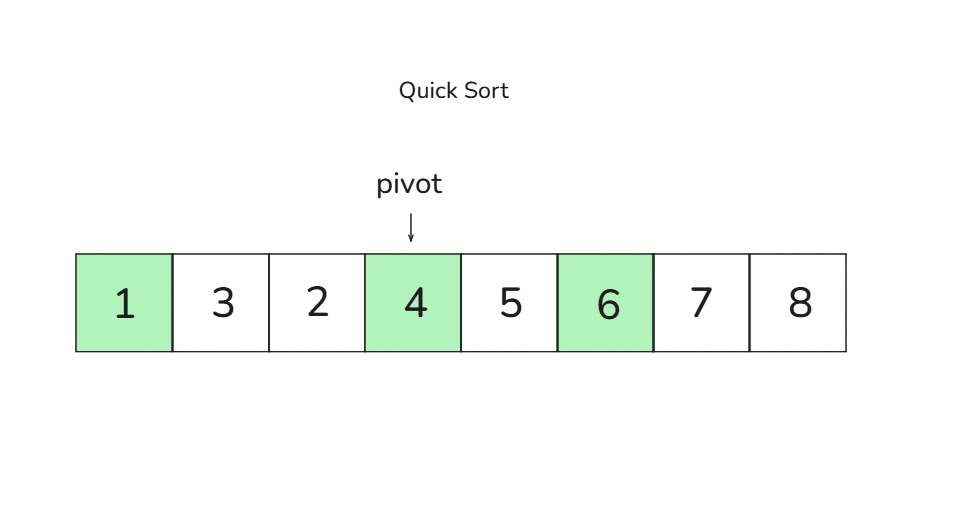
이제 [3, 2]와 [5]로 나뉘어집니다

🎈 4회차 비교 과정 (왼쪽 그룹: [3, 2]):

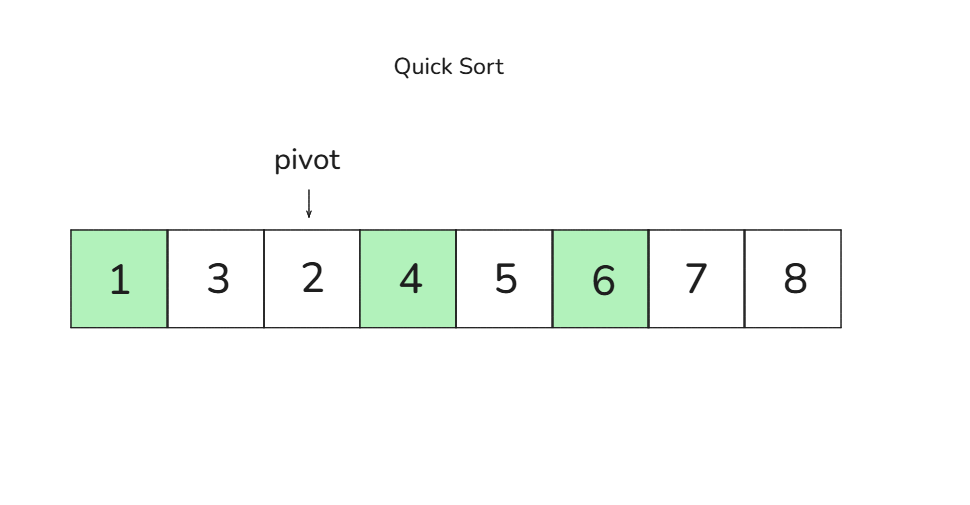
다음 피벗은 2입니다.

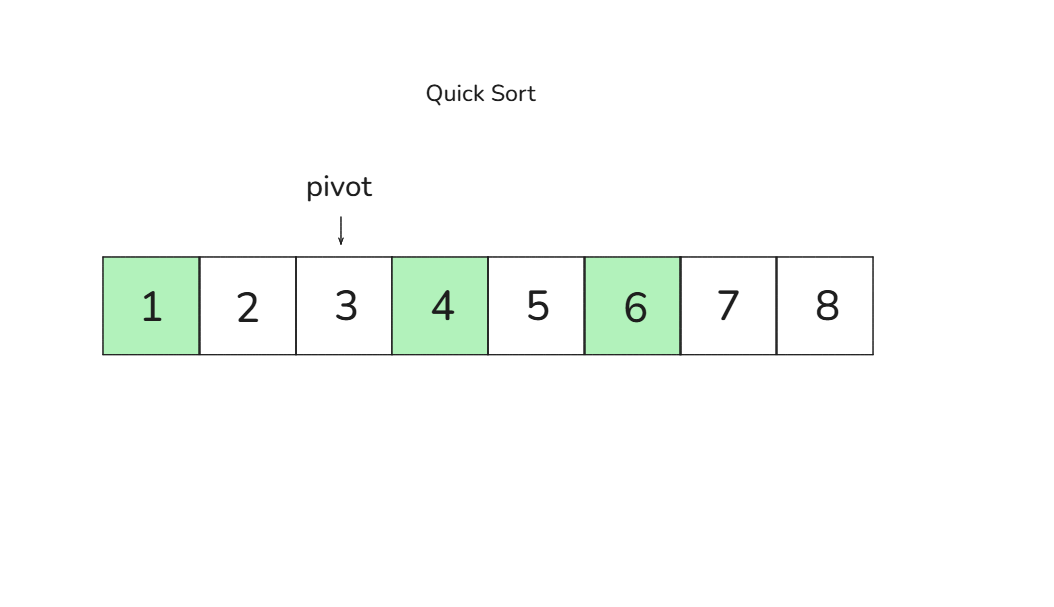
• 왼쪽에서 3이 피벗보다 크고 오른쪽은 값이 없으므로 피벗과 교환합니다 → [2, 3]

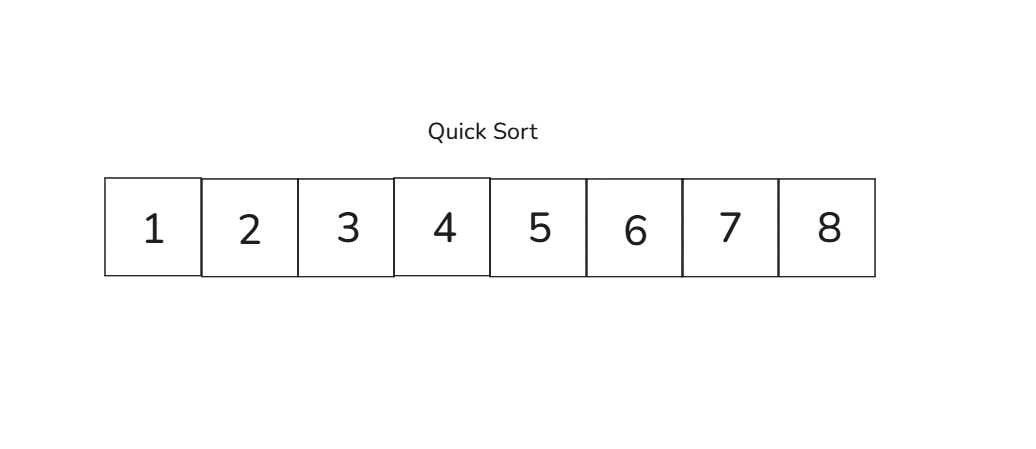
이렇게 각 그룹이 더 이상 나눠질 수 없을 때까지 반복하면, 정렬이 완성됩니다
이제 모든 숫자가 오름차순 정렬되었습니다 [1, 2, 3, 4, 5, 6, 7, 8]

🛠️ 퀵정렬의 시간복잡도

• 평균 시간복잡도: O(nlogn)
• 최악의 시간복잡도: O(n²) (피벗 선택이 편향될 경우)
• 최상의 시간복잡도: O(nlogn)

📌장점

• 평균적으로 O(n log n )이라는 빠른 실행시간을 가집니다
• in-place 정렬이 가능하기 때문에 추가적인 메모리 사용이 없습니다
• 대규모 데이터 셋에서 효율적으로 동작합니다

📌단점

• 피벗 선택이 편향되는 최악의 경우 성능이 저하됩니다
• 안정정렬이 아니라 원본 순서를 보장하지 않습니다

✍️결론

퀵정렬은 피벗을 이용하여 빠르고 효율적으로 정렬하는 방법입니다

평균적으로 빠른 실행시간을 가진다는 장점으로 많이 사용하지만,
피벗 선택이 편향되는 경우 성능이 저하된다는 단점이 존재합니다