다양한 정렬 알고리즘
지금까지 총 6가지 정렬 알고리즘을 학습했습니다.
Bubble 정렬, Selection 정렬, Insertion 정렬, Merge 정렬, Heap 정렬, Quick 정렬입니다
각각의 정렬 알고리즘은 사용 상황과 데이터 크기에 따라 장단점이 명확합니다
이번에는 지금까지 정리한 정렬 알고리즘들의 특징을 비교하겠습니다
🔍 기존 정렬 알고리즘 비교
✨느린 정렬 알고리즘 (평균 시간 복잡도 O(n²))
Bubble 정렬, Selection 정렬, Insertion 정렬은 평균적인 상황에서 정렬 시간이 오래 걸리는 알고리즘입니다
구현이 쉽지만 성능이 좋지 않기 때문에 큰 데이터에서는 효율성이 떨어집니다
✨ 빠른 정렬 알고리즘 (평균 시간 복잡도 O(nlogn))
Merge 정렬, Heap 정렬, Quick 정렬은 평균적으로 빠른 성능을 가집니다
앞선 느린 정렬 알고리즘들보다 큰 데이터에서는 해당 정렬 사용하는 것이 좋습니다
📌평균 시간 복잡도의 의미는?
그런데 평균 시간 복잡도가 동일한 O(nlogn)이라도 실제로 정렬시간은 다를 수 있습니다
당장 바로 이전 글에서 Heap 정렬 알고리즘과 Quick 정렬 알고리즘의 동작 시간을 비교했을 때,
평균 동작 시간이 다른 것을 확인했던 것처럼 말입니다
평균 시간복잡도가 같지만 실행시간의 차이가 생기는 이유는 실제 수행시간을 계산했을 때의 값이 다르기 때문입니다
여기서 중요한 요소가 바로 시간 복잡도의 상수항, 즉 C 값입니다
실제 수행 시간은 다음과 같이 나타낼 수 있습니다.
C × nlogn + α
여기서 α는 상대적으로 작은 값이므로 무시할 수 있지만,
C는 알고리즘의 특성에 따라 매우 큰 차이를 만들어냅니다
그리고 이 C 값에 큰 영향을 주는 핵심적인 요소가 참조 지역성(Locality of Reference)입니다
🚀 C와 α는 무엇을 의미할까?
C는 연산 1회당 걸리는 시간을 의미합니다
비교, 대입, 메모리 접근 등의 단위 연산 비용이 모두 C에 포함됩니다
α는 초기 설정 시간을 의미합니다. 입력 크기와 무관하며,
함수 초기화 캐시 로딩 등 알고리즘 동작 전에 한번만 실행되는 초기 세팅 시간입니다
α는 제어하기 힘든 영역이기 때문에 일반적으로 무시되기 때문에
일반적으로 C의 크기가 알고리즘의 성능을 좌우합니다
즉, C가 작을 수록 알고리즘 실행 시간이 빨랍니다
🚀 참조 지역성 (Locality of Reference)이란?
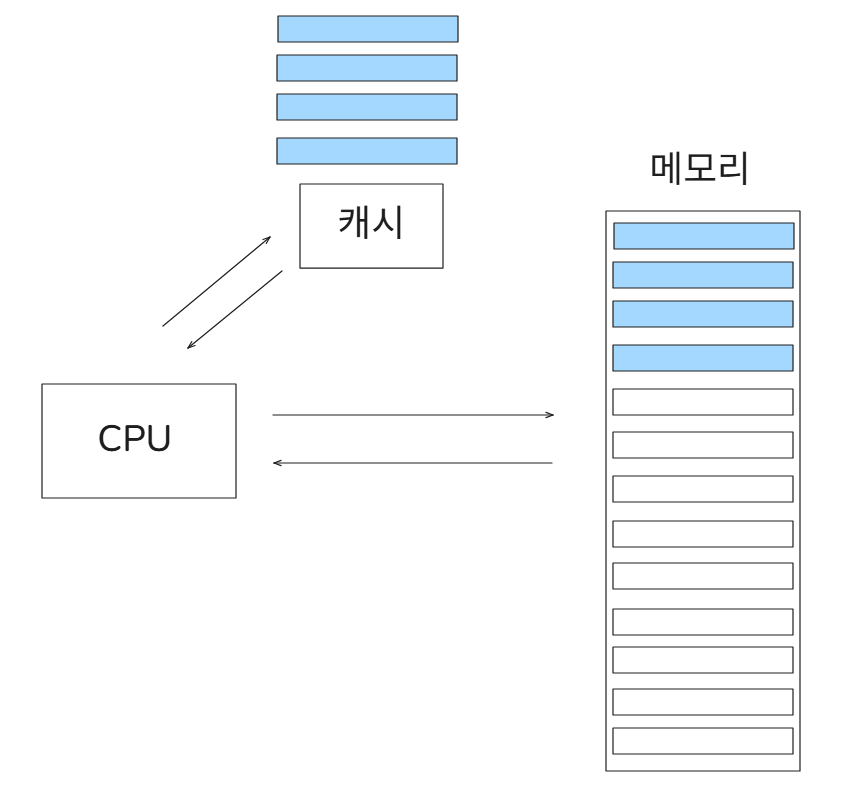
CPU는 데이터를 빠르게 가져오기 위해 예측하여 캐시 메모리에 데이터를 저장해 둡니다
캐시 메모리는 메인 메모리보다 훨씬 빠르게 접근할 수 있기 때문입니다
이때 CPU가 미래에 사용할 데이터를 예측하는 정확도를 높이는 방법이 참조 지역성입니다
즉, 최근 사용한 메모리나 인접한 위치의 데이터를 다시 사용할 가능성이 크다는 원리에 따라 데이터를 캐시에 미리 담아 두는 것입니다
참조 지역성을 잘 만족할수록 알고리즘의 실제 동작 속도가 빨라집니다
📌 빠른 정렬 알고리즘의 참조 지역성 비교
🛠️ Heap 정렬
Heap 정렬은 힙 자료구조를 기반으로 합니다
힙의 특성상 한 위치의 요소를 자신의 인덱스 두 배 또는 절반에 위치한 요소와 계속 비교합니다
이러한 참조 방식은 메모리의 접근 위치가 멀리 떨어져 있어서 캐시 메모리에 담기 어렵기 때문에 참조 지역성을 잘 만족하지 못합니다
따라서 C 값이 비교적 크며, 실제 성능이 다른 알고리즘보다 떨어질 수 있습니다
🛠️ Merge 정렬
Merge 정렬은 인접한 블록을 반복적으로 병합합니다
즉, 연속적인 메모리 접근이 많아 참조 지역성의 원리를 어느 정도 잘 만족하는 알고리즘입니다
그러나 추가적인 메모리가 필요하다는 단점이 있습니다
🛠️ Quick 정렬
Quick 정렬은 pivot 값을 기준으로 데이터 위치를 빠르게 변경합니다
일반적으로 pivot 주변에서 데이터 접근이 이루어지기 때문에 참조 지역성의 원리를 만족합니다
따라서 실제로도 C 값이 가장 작은 편이며, 평균적으로 가장 빠른 성능을 나타냅니다
그러나 pivot을 잘못 선정할 경우 최악의 경우 O(n²)이 될 수도 있는 단점이 존재합니다
🔑 새로운 정렬 알고리즘의 필요성
지금까지 살펴본 것처럼 기존의 알고리즘들에는 모두 장단점이 명확합니다
- Heap 정렬은 참조 지역성이 떨어지고 실제 성능이 다른 정렬 알고리즘에 비해 떨어집니다
- Merge 정렬은 참조 지역성은 좋으나 추가 메모리 부담이 큽니다
- Quick 정렬은 참조 지역성이 좋고 빠르지만, 최악의 상황에서 성능 저하 위험이 존재합니다
이러한 한계를 극복하고 조건을 만족하는 새로운 정렬 알고리즘이 필요하게 되었습니다
- 상수(C 값)가 크지 않아 실제 성능이 우수한 알고리즘
- 추가적인 메모리를 최소한으로 사용하는 알고리즘
- 최악의 경우에도 O(nlogn)을 보장하는 알고리즘
이러한 조건을 만족하는 알고리즘이 바로 팀 정렬(Tim Sort) 알고리즘입니다.
✍️ 결론
같은 시간복잡도를 갖더라도 동일한 성능을 보장하지 않습니다
참조 지역성, 메모리 사용량, 최악의 상황등 다양한 요소를 고려해야 합니다
그리고 이러한 요소를 고려한 알고리즘이 바로 팀 정렬(Tim Sort) 알고리즘입니다
