서론

금일 알고리즘 스터디에서 다룬 차수의 개념을 바탕으로
그래프 이론의 기초적인 내용을 정리했습니다.

그래프 이론 기초

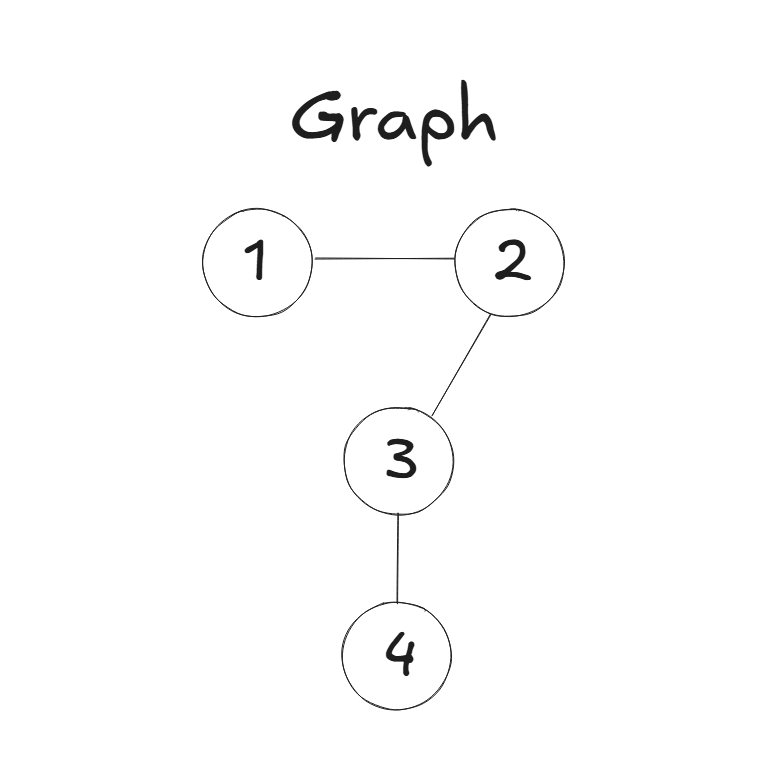
그래프는 정점과 간선의 집합으로 이루어진 구조입니다.

정점과 간선 (Vertex and Edge)

아래와같이 동그라미는 정점이고, 각 정점 간의 연결을 간선이라고 합니다

차수 (Degree)

각 정점에 연결되어 있는 간선의 개수를 차수라고 합니다

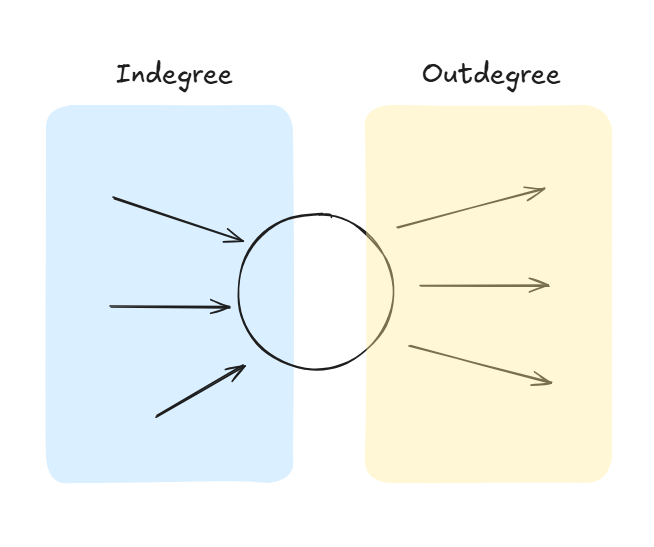
차수는 간선의 방향에 따라 indegree, outdegree로 나뉩니다

• Indegree: 정점으로 들어오는 간선의 개수
• Outdegree: 정점에서 나가는 간선의 개수

그래프 구분 방법

그래프는 다음 3가지 기준으로 구분합니다.

• 방향의 유무
• 가중치의 유무
• 정점의 종류

방향의 유무

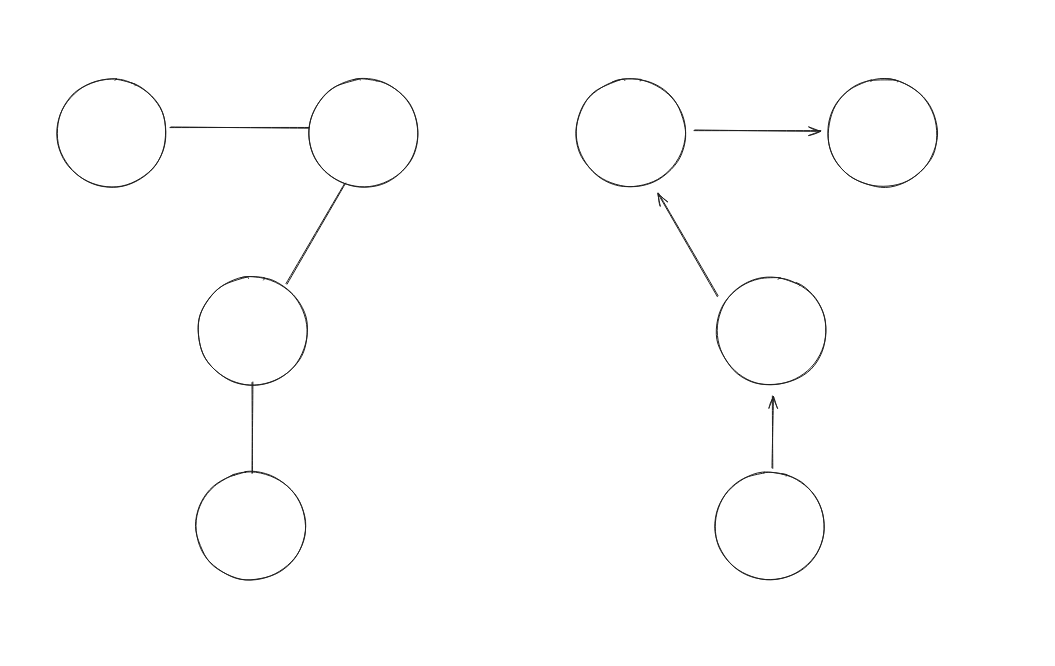
간선에 방향이 있는지 없는지 두가지로 구분할 수 있습니다
왼쪽은 무방향 그래프, 오른쪽은 방향 그래프입니다

• 방향 그래프(Directed Graph): 간선에 방향이 존재하는 그래프
• 무방향 그래프(Undirected Graph): 간선에 방향이 없는 그래프

무방향 그래프는 구현할 때 보통 양방향으로 간주합니다

가중치의 유무

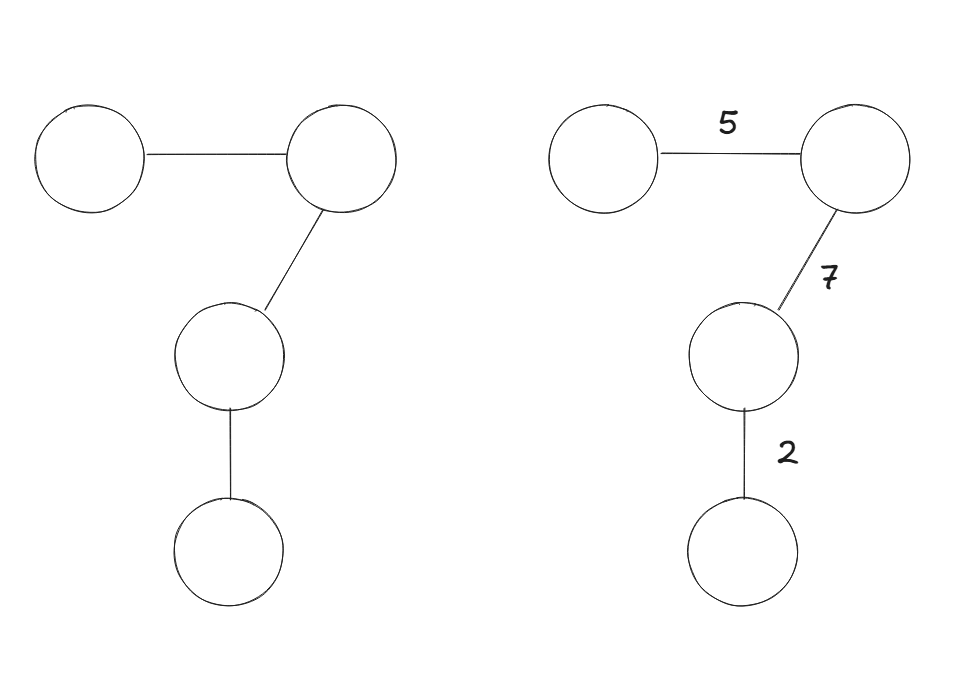
가중치의 유무에 따라 그래프를 구분할 수 있습니다
여기서 가중치는 간선의 이동비용입니다

왼쪽은 가중치가 없는 그래프, 오른쪽은 가중치가 있는 그래프입니다

정점의 종류

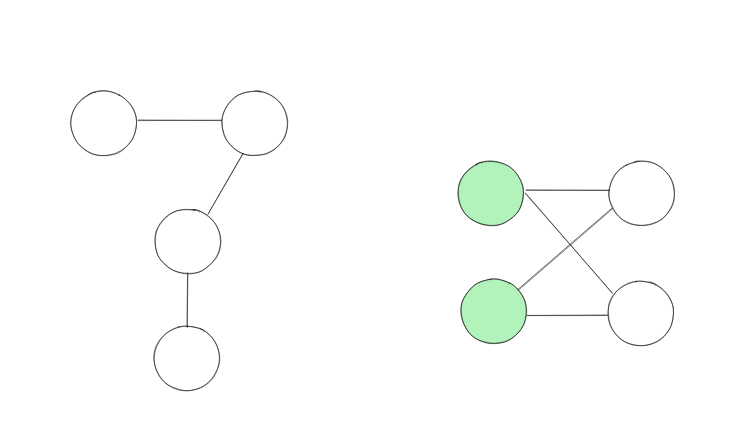
정점의 종류에 따라서도 구분할 수 있습니다

• 동종 그래프: 모든 정점이 같은 종류로 구성된 그래프
• 이종 그래프: 서로 다른 종류의 정점으로 구성된 그래프

이종 그래프는 른 종류의 정점 간에만 간선이 연결됩니다

정리

• 그래프는 정점과 간선으로 이루어진 구조입니다.
• 정점에 연결되어 있는 간선의 개수를 차수라고 합니다.
• 정점으로 들어오는 간선의 개수는 Indegree, 정점에서 나가는 간선의 개수는 Outdegree입니다
• 그래프를 구분하는 기준은 방향의 유무, 가중치의 유무, 정점의 종류입니다