카운팅 정렬

정의

항목들의 순서를 결정하기 위해 집합에 각 항목이 몇 개씩 있는지 세는 작업을 하여,
선형 시간에 정렬하는 효율적인 알고리즘

제한 사항

• 정수나 정수로 표현할 수 있는 자료에 대해서만 적용 가능 : 각 항목의 발생 회수를 기록하기 위해, 정수 항목으로 인덱스 되는 카운트들의 배열을 사용하기 때문
• 카운트들을 위한 충분한 공간을 할당하려면 집합 내의 가장 큰 정수를 알아야 한다.

시간 복잡도

• O(n + k): n은 리스트 길이, k는 정수의 최대값

[0, 4, 1, 3, 1, 2, 4, 1] 을 카운팅 정렬하는 과정

Data에서 항목들의 발생 회수를 세고, 정수 항목들로 직접 인덱스 되는 카운트 배열 counts에 저장한다.

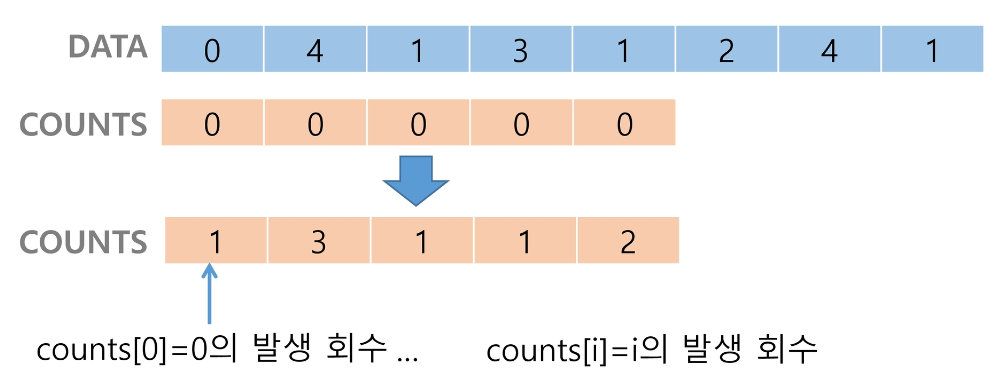
정렬된 집합에서 각 항목의 앞에 위치한 항목의 개수를 반영하기 위해 counts의 원소를 조정한다.

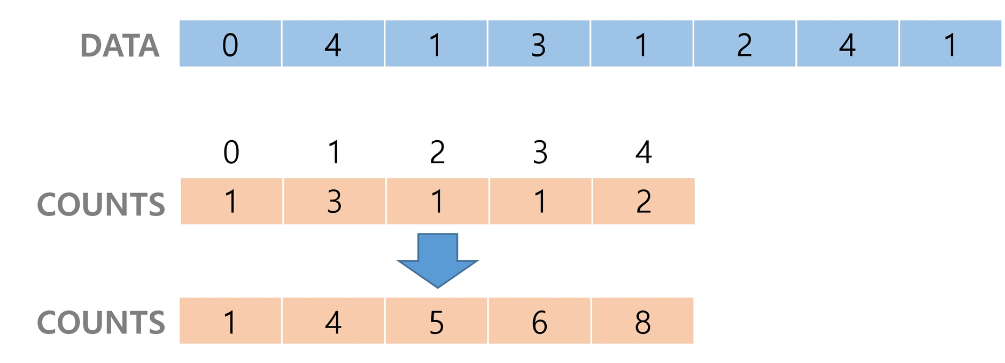
counts[1]을 감소시키고 temp에 1을 삽입한다.

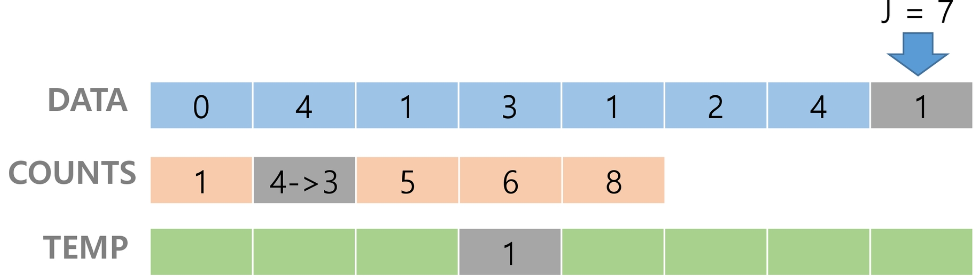
counts[4]를 감소시키고 temp에 4를 삽입한다.

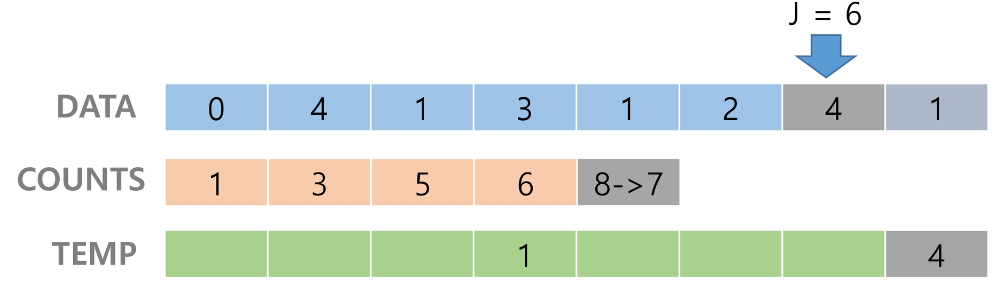
counts[2]를 감소시키고 temp에 2를 삽입한다.

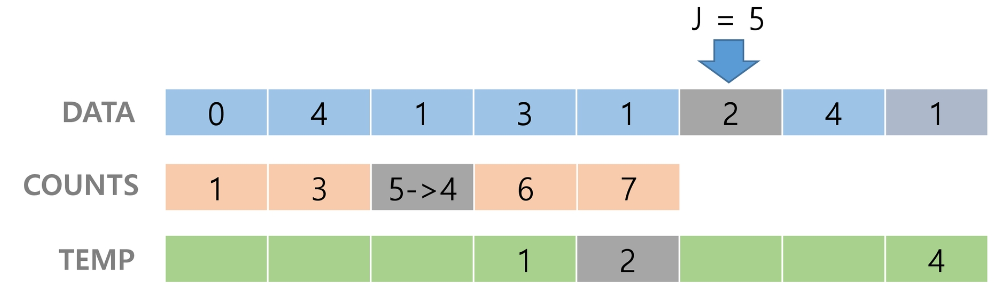
counts[1]을 감소시키고 temp에 1을 삽입한다.

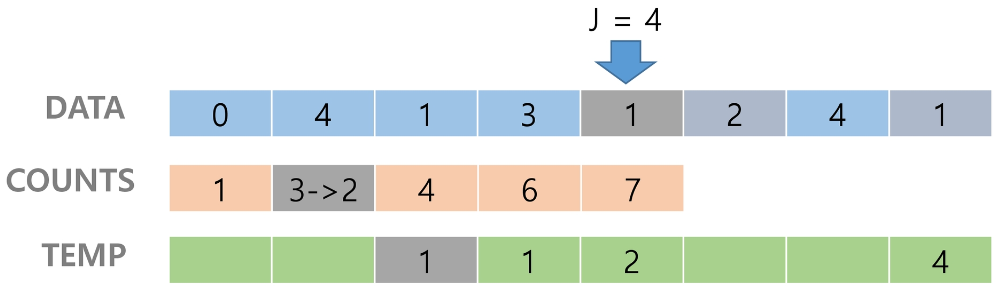
counts[3]을 감소시키고 temp에 3을 삽입한다.

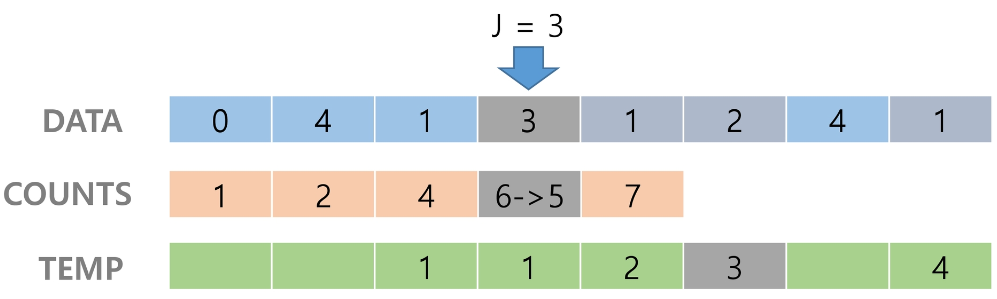
counts[1]을 감소시키고 temp에 1을 삽입한다.

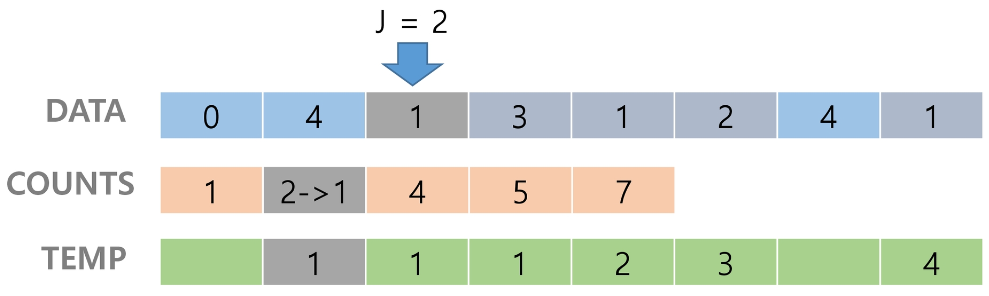
counts[4]를 감소시키고 temp에 4를 삽입한다.

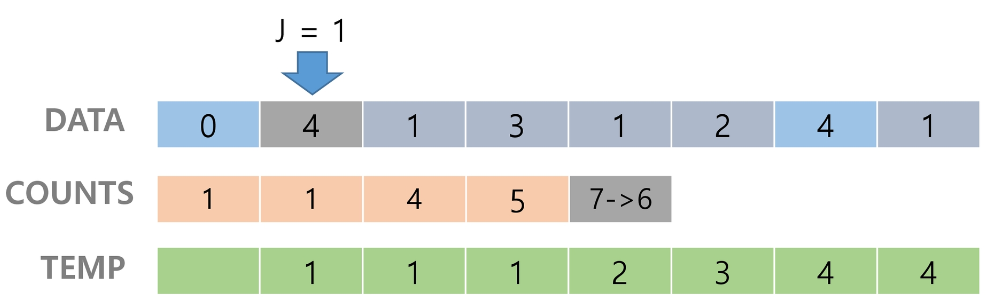
counts[0]을 감소시키고 temp에 0을 삽입한다.

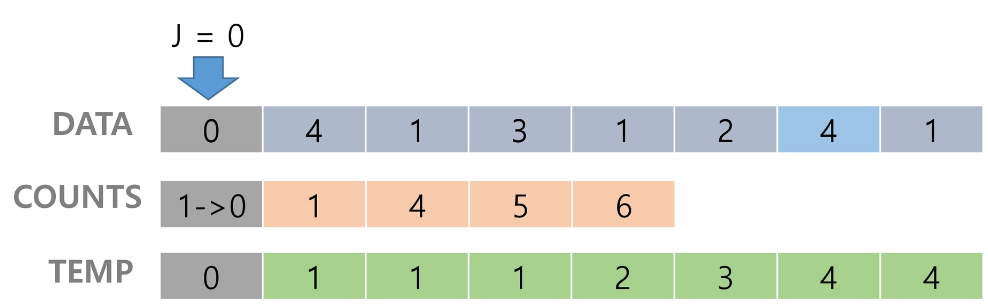
temp 업데이트 완료하고 정렬 작업을 종료한다.

코드로 표현

def Countiing_Sort(DATA, TEMP, k)
    # DATA[] -- 입력 배열
    # TEMP[] -- 정렬된 배열
    # COUNTS[] -- 카운트 배열
    
    COUNTS = [0] * (k + 1)
    
    for i in range(0, len(DATA)):
        COUNTS[DATA[i]] += 1
    
    for i in range(1, k + 1):
        COUNTS[i] += COUNTS[i - 1]
        
    for i in range(len(TEMP) - 1, -1, -1):
        COUNTS[DATA[i]] -= 1
        TEMP[COUNTS[DATA[i]]] = DATA[i]

버블정렬보다 복잡한거 같은데 카운팅 정렬을 왜 쓰나요?

• 바로 시간 복잡도 떄문입니다.
• 버블 정렬은 코딩을 손쉽게 할 수 있는 대신, 시간 복잡도가 O[n^2]로 꽤 높은 편 (비교와 교환)
• 카운팅 정렬은 코딩 난이도가 어려운 대신, 시간 복잡도가 O[n]으로 낮음 (비교환 방식)