MFCC란
오디오 신호에서 추출할 수 있는 feature이다. 소리의 고유한 특징을 나타내는 수치다.
MFCC 과정
Audio Signal
시간에 따른 파형을 나타내는 오디오 신호이다.
Framing
연속된 오디호 신호를 일반적으로 1frame당 20~40ms로 나눈다.
그 이유는 짧은 시간 내에서도 오디오 신호는 변하지만 해당 크기의 구간 내에서의 변화는 전체적인 관점으로 봤을 때 영향이 크지 않다.
또, frame을 나눌 때 약 50%(10~20ms)를 겹치게 설정하여 프레임의 불연속을 막는다.(windowing도 같은 용도로 사용된다.)
Windowing
각 프레임에 함수를 곱하여 프레임의 경계에서 갑작스러운 변화로 인한 왜곡을 방지한다.
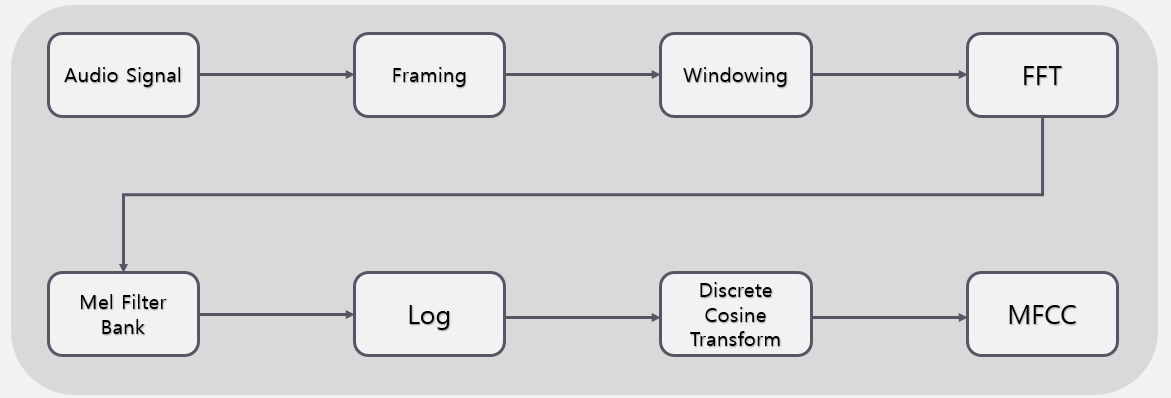
오디오 신호에서는 주로 Hamming Window 함수를 사용한다.
Hamming Window
신호의 경계에서 불연속을 막기 위해 사용된다.
-
수식
-
그래프
신호를 frame 단위로 나눌 때 경계 부분에서 갑작스러운 변화로 인한 경계의 불연속을 막고, 양 끝 경계 값에 0에 가까운 값을 곱하여 주파수 성분이 잘 분리될 수 있게 하여 신호의 주파수 분석 성능을 향상시킬 수 있다.
이 때 갑작스러운 변화는 고주파 성분으로 나타나게 되고 이를 리플(Ripple) 또는 사이드로브(Sidelobe) 효과라고 한다.
FFT(Fast Fourier Transform)
푸리에 변환을 빠르게 수행하는 알고리즘이다.
DFT(Discrete Fourier Transform)
시간에 따라 변화하는 이산적인 디지털 신호를 주파수 성분으로 분해하는 기법이다.
- : 시간 도메인에서의 신호
- : 주파수 도메인에서의 성분
- : 신호의 샘플 수
- : 각 주파수 성분의 인덱스
- : 복소수 단위로,
- : 주파수 성분의 회전각을 결정하는 인자(시간 도메인에서의 신호 샘플이 특정 주파수 성분에 얼마나 기여하는지 결정하는 인자)
- 오일러 공식에 의해 로 변환된다. 이 수식은 복소 평면에서 신호를 특정 주파수로 회전시키는 역할을 한다.
- 회전의 의미 : 각 에 대해 번째 샘플이 기여하는 정도를 나타내며, 시간 도메인에서 특정 주파수 성분이 신호에 어떻게 나타나는지를 나타낸다.
계산 복잡도
DFT의 계산 복잡도는 이지만, FFT를 사용하게 되면 로 줄어든다.
FFT는 분할 정복을 사용하여 신호를 재귀적으로 작은 부분으로 나눈 후, 각각에 대해 DFT를 수행한 뒤 결과를 결합하는 방식을 사용한다.
Cooley-Tukey 알고리즘
FFT 수행시 주로 사용되는 분할 정복 알고리즘으로, 신호를 짝수와 홀수 샘플로 나누어 각각에 대해 DFT를 수행하고 결과를 결합하는 방식이다.
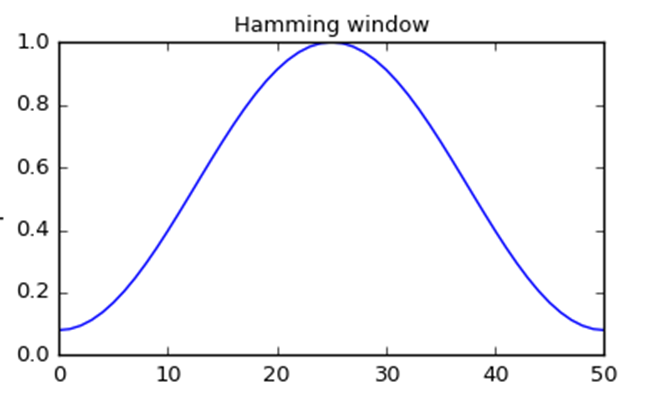
Mel Scale
주파수를 인간의 청각이 인식하는 방식으로 변환하는 scale 변환 함수이다.
인간의 청각은 저주파수에 대해서는 예민하게 반응하지만, 고주파수에서는 덜 민감하게 반응한다.
예를 들어, 100Hz와 200Hz는 잘 구분하지만, 1000Hz와 1100Hz는 잘 구분하지 못 한다.
-
수식
- : Hz 단위의 주파수
- : Mel 스케일을 통해 변환된 주파수
-
그래프
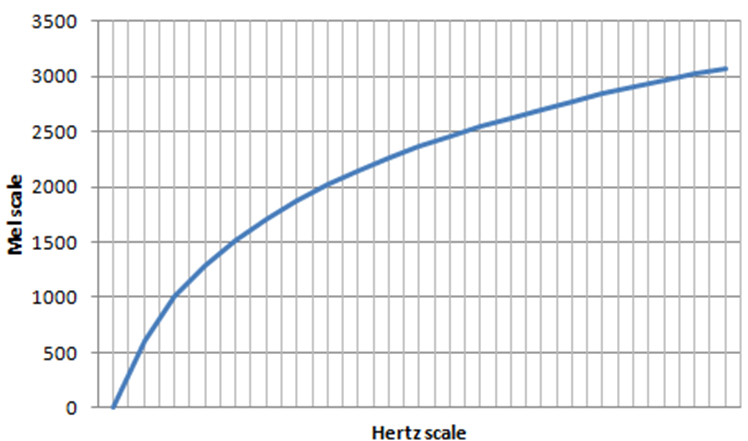
Mel Filter Bank
Mel Scale 변환 함수를 통해 주파수 대역을 분할한 후, 각 대역에서의 주파수 성분을 추출하는데 사용되는 삼각 필터이다.
FFT를 통해 얻은 (주파수 도메인으로 변환된) 음성 신호에 Mel Filter Bank를 적용한다. 각 필터는 특정 주파수 대역에 해당하는 성분을 증폭하거나 억제한다. 이 때 Mel Filter Bank를 정의해야 하는데, 개수에 따라 필터의 형태가 바뀐다.
-
수식
- : 번째 Mel Filter의 출력
- : FFT의 결과로, 주파수 성분의 크기
- : 번째 Mel Filter의 함수 값
-
그래프
Log 변환
Mel Filter Bank를 거치게 되면, 각 필터의 출력은 특정 주파수 대역의 에너지를 나타낸다. 이 에너지를 스펙트럼의 크기로 표현할 수 있다.
-
수식
-
Log 변환의 특징
- 인간의 청각 특성 반영
- 인간의 청각은 소리의 강도에 로그 스케일로 반응하기 때문에 로그 변환을 통해 그 특성을 반영할 수 있다.
- 스펙트럼 압축
- 고에너지 성분의 크기를 줄이고, 저에너지 성분의 크기를 키우면서 성분 간의 차이를 줄일 수 있다. 이를 통해 오디오 정보를더 잘 포착할 수 있다.
- 잡음 감소
- 저에너지 대역에 존재하는 잡음을 더 작게 표현하고, 고에너지 대역에 있는 신호를 자세히 포착할 수 있다.
- 인간의 청각 특성 반영
여기까지 수행한 결과를 Mel Spectrogram이라고 한다. 이후 밑에서 자세히 설명할 것이다.
DCT(Discrete Cosine Transform)
멜 스펙트로그램을 압축하고, 주파수 정보를 특징 벡터로 변환하는 단계이다.
주파수 도메인에서 시간 도메인으로 변환하여, 고차원 데이터를 저차원 특징 벡터로 압축한다. 이 과정을 통해 멜 스펙트로그램을 간단하게 표현할 수 있다.
-
수식
- : 번째 DCT 계수로, 시간 프레임 에 대한 번째 켑스트럼 계수
- : 시간 프레임 에서 멜 스펙트로그램의 번째 멜 필터의 로그 에너지
- : 멜 필터 뱅크의 개수
- : DCT 차수
-
DCT의 역할
- 고차원 주파수 정보를 저차원으로 압축
- 멜 스펙트로그램을 압축하여 가장 중요한 정보만 담은 저차원 벡터로 변환한다. 이로 인해 계산의 효율성이 증가한다.
- 상관관계 제거
- 멜 스펙트로그램은 인접한 주파수 대역 간의 높은 상관관계를 가질 수 있다. DCT를 거치게 되면 상관관계가 줄어든다. 이는 AI 학습 성능을 향상시킬 수 있다.
- 주파수 성분 압축
- 에너지를 낮은 차수의 계수에 집중시켜, 저주파수 성분이 강조되어 음성 신호의 중요한 특징을 더 명확하게 표현할 수 있다.
- 고차원 주파수 정보를 저차원으로 압축
MFCC(Mel Frequency Cepstral Coefficient)
DCT의 결과물인 계수들 중 일부를 선택하여 MFCC를 생성한다. 주로 13차원을 사용한다.
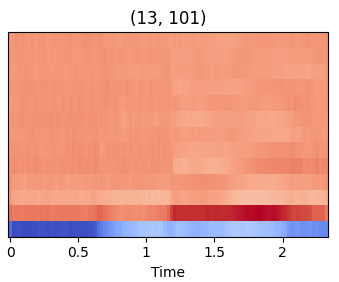
- MFCC 계수의 특징
- 0번째 계수(C0)
- 신호의 전체적인 에너지를 의미한다. 즉, 전체적인 신호의 강도를 나타낸다.
- 1번째 계수(C1)
- 저주파수 성분을 나타낸다.
- 목소리 톤, 성별, 나이 등과 같은 음색에 관한 정보를 담고 있다.
- 성대의 진동과 관련된 기본 주파수와 밀접하게 연결되어 있다.
- 2번째 ~ 12번째 계수(C2 ~ C12)
- 중간 및 고주파수 성분을 나타낸다.
- 음성 신호의 포먼트 구조를 나타내고, 발음의 구별에 중요한 역할을 한다.
- 포먼트는 성도에서 발생하는 공명 주파수로, 각각의 계수가 특정 주파수 대역에서 신호의 에너지를 표현한다.
- C2 ~ C4 : 저주파수 및 중간 주파수, 모음과 같은 음소를 구별하는데 중요한 정보를 제공한다.
- C5 ~ C12 : 음성의 미세한 주파수 변화를 반영하고, 구체적인 발음의 특징을 나타낸다.
- 델타, 델타-델타 계수
- 델타 : MFCC의 시간적 변화 / 델타-델타 : 델타의 시간적 변화
- 시간적 변화를 추척할 수 있다.
- 발음의 변화율을 계산하는데 사용된다.
- 0번째 계수(C0)
Mel Spectrogram
MFCC 과정에서 log 변환까지 진행된 것이 멜 스펙트로그램이다.
시간에 따른 진폭의 변화와 주파수에 따른 진폭의 변화를 동시에 볼 수 있다.
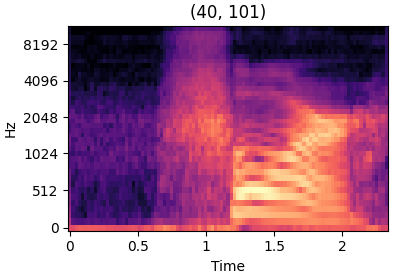
- Mel Spectrogram의 특징
- 시각적 분석
- 시간-주파수 정보를 시각화하는데 매우 유용하다.
- 시각적 분석
