트리 (Tree)

트리(Tree)는 계층적인 구조를 표현하는 자료구조로, 노드(node)들이 간선(edge)으로 연결된 형태를 가지며 하나의 루트(root) 노드를 가진다. 트리는 컴퓨터 과학에서 매우 중요한 자료구조로 다양한 응용 분야에서 활용된다.

트리의 구조

• 루트 노드 : 트리의 최상위에 위치하는 노드로, 모든 경로의 시작점
• 부모-자식 관계 : 각 노드는 부모-자식 관계를 가지며, 부모 노드에서 자식 노드로의 방향성을 가짐
• 계층 구조 : 노드들은 부모와 자식 관계를 통해 계층적으로 구성됨
• 리프 노드 : 자식이 없는 노드로, 트리의 가장 하위에 위치

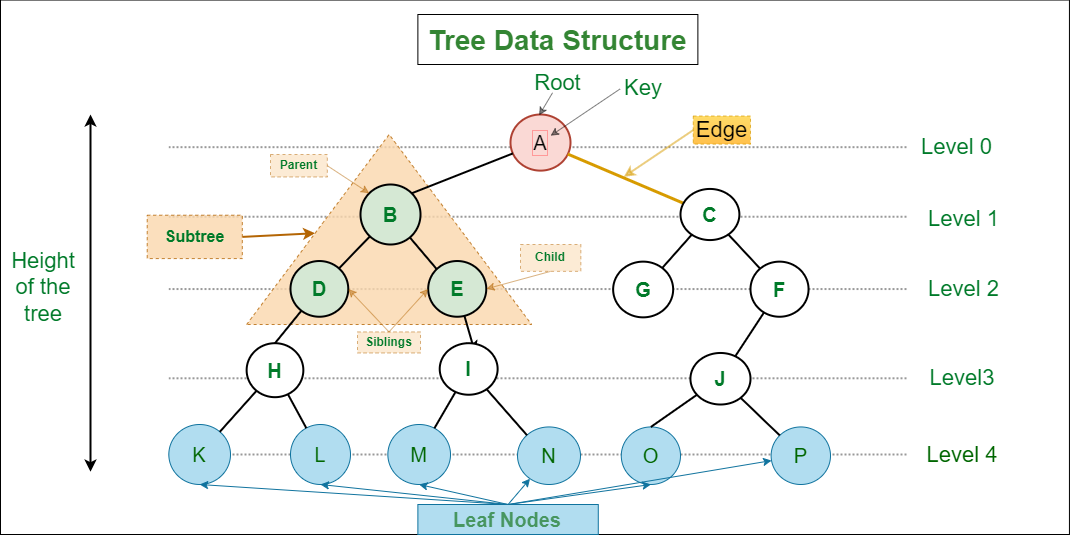
용어

• 노드(Node) : 트리를 구성하는 기본 요소로, 계층구조를 형성하며 서로 연결됨
• 간선(Edge) : 노드와 노드를 연결하는 선
• 루트(Root) : 트리의 최상위 노드
• 부모(Parent) : 어떤 노드의 바로 위에 있는 노드
• 자식(Children) : 어떤 노드의 바로 아래에 있는 노드
• 조상(Ancestor) : 특정 노드에서 루트까지의 경로 상에 있는 모든 노드들
• 자손(Descendant) : 특정 노드에서 해당 노드까지의 경로 상에 있는 모든 노드들
• 형제(Sibling) : 같은 부모를 가지는 노드들
• 높이(Height) : 트리의 최대 레벨 수
• 깊이(Depth) : 특정 노드에서 루트까지의 경로의 길이

특성

1. 계층 구조 : 트리는 부모-자식 관계를 가진 노드들로 이루어진 계층적인 구조로, 각 노드는 자신의 부모와 자식 노드를 가지고 이러한 구조는 데이터의 계층화를 효과적으로 표현할 수 있다.

2. 단일 경로 : 트리에서 두 노드를 연결하는 경로는 유일하다. 부모 노드에서 자식 노드로든 가는 경로는 오직 한 가지로, 그 연결선이 edge가 된다.

3. 비순환적 구조 : 트리의 어떤 경로를 따라가도 동일한 노드를 두 번 이상 방문하지 않는다.

4. 유일한 루트 노드 : 모든 트리는 단 하나의 루트 노드를 가진다. 루트 노드는 트리의 시작점이며, 모든 다른 노드는 루트 노드로부터의 어떠한 경로를 통해 접근 가능하다.

5. 서브 트리(Subtree) : 트리 내의 어떤 노드와 그 자손들로 이루어진 부분 트리로, 어떤 노드를 루트로 하는 서브 트리는 그 노드의 자식들과 그 자식들의 자손들로 이루어진다.

트리의 종류

이진 트리 (Binary Tree)

이진 트리는 노드들이 최대 두 개의 자식을 가지며, 루트 노드를 시작으로 각 노드들이 서로 연결된 구조의 트리를 말한다. 최대 두 개의 자식을 가지므로 자식이 없을 수도, 1개만 가질 수도 있다. 이진 트리 중 구조와 특징에 따라 완전 이진트리, 편향 이진트리, 포화 이진트리 등으로 분류될 수 있다. 다음은 흔히 사용되는 이진 트리의 일종이다.

이진 탐색트리 (Binary Search Tree)

이진 탐색 트리(Binary Search Tree)는 이진 트리의 일종으로, 다음 조건을 만족하는 트리이다.

1. 왼쪽 서브트리의 모든 노드들의 값은 해당 노드의 값보다 작다.
2. 오른쪽 서브트리의 모든 노드들의 값은 해당 노드의 값보다 크다.
3. 모든 노드의 왼쪽, 오른쪽 서브트리 모두 이진 탐색 트리를 만족한다.

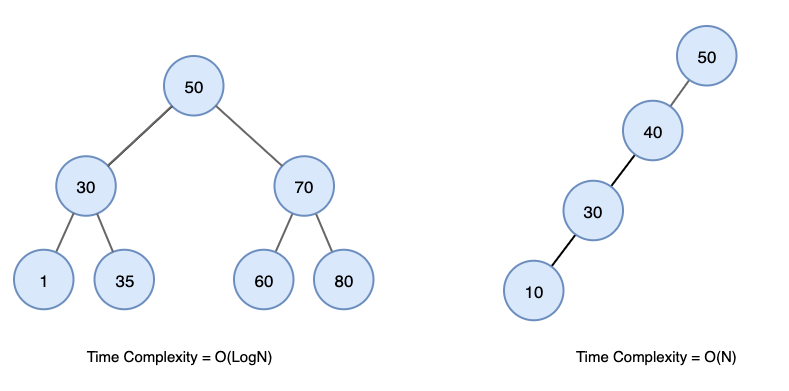
이런 특성을 활용해 재귀적으로 트리를 순회하여 탐색, 삽입, 삭제 등의 연산을 효율적으로 수행할 수 있고 데이터를 정렬된 상태로 유지할 수 있다. BST의 탐색 연산은 평균적으로 O(log n)의 시간복잡도를 가지므로 효율적으로 수행된다고 볼 수 있다. 최악의 경우(편향된 트리일 경우) O(n)의 시간복잡도를 가질 수 있다.

힙 (Heap)

힙(Heap)은 완전 이진트리(마지막 레벨을 제외한 모든 레벨이 가득 채워져 있으며 마지막 레벨 노드들이 왼쪽부터 순차적으로 채워진 트리)를 만족하며, 왼쪽 자식은 해당 노드보다 작은 값을, 오른쪽 자식은 해당 노드보다 큰 값을 가지는 조건을 만족한다. 최대 힙(MaxHeap) 은 부모 노드의 값이 자식 노드의 값보다 크거나 같으며, 최소 힙(MinHeap) 은 부모 노드의 값이 자식 노드의 값보다 작거나 같다.

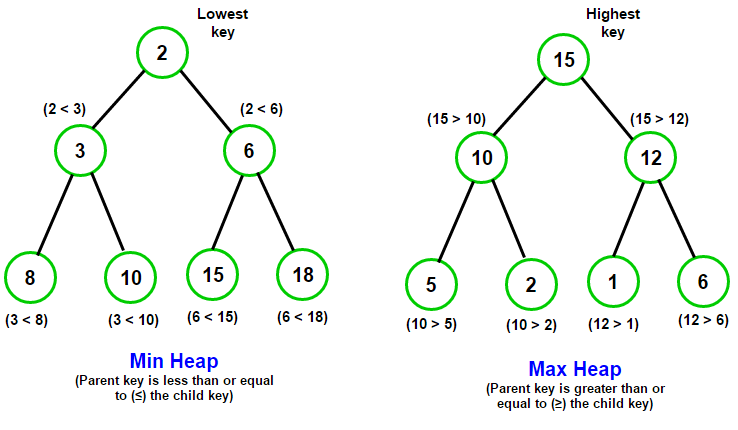
기존 배열에서 최대/최소값을 찾기 위해서는 O(n)이 소요되지만 힙에서는 O(logn)만큼 소요되는, 주어진 데이터에서 최대/최소값을 빠르게 찾기 위해 고안된 이진 트리이다.

Binary Search Tree vs Heap

힙과 BST 모두 이진 트리의 일종이기 때문에 헷갈릴 수 있지만 목적과 동작 방식에 있어 차이를 가진다.

• BST는 탐색 연산에 중점을 둔 자료구조로, 기준 노드를 기준으로 왼쪽 서브트리는 모두 작고 오른쪽 서브트리는 모두 큰 값을 가진 노드들이 존재하기에 이를 활용해 탐색을 수행한다. 하지만 힙은 최대/최소값에 빠르게 접근하기 위한 자료구조로, 루트 노드가 목표로 하는 최대/최소값이므로 이에 접근할 수 있다.
• 힙은 BST와 달리 왼쪽/오른쪽 서브트리가 기준 노드보다 모두 작거나/큰 성질을 만족하지 않는다. 단순히 부모-자식 간의 관계에서 최대힙/최소힙 성질만을 만족한다.

AVL 트리

AVL 트리는 자가 균형 이진 탐색 트리로, 스스로 균형을 유지하는 트리 구조이다. 위의 BST 자료처럼 이진 탐색 트리에서 데이터가 편향된 경우, 즉 한 쪽으로 치우쳐진 경우 탐색에 O(n)의 시간이 소요될 수 있다. 이렇게 편향된 이진 트리는 트리의 높이가 높아져 탐색에 오랜 시간이 소요되는데, AVL 트리에서는 이를 방지하기 위해 균형을 유지하고자 한다.

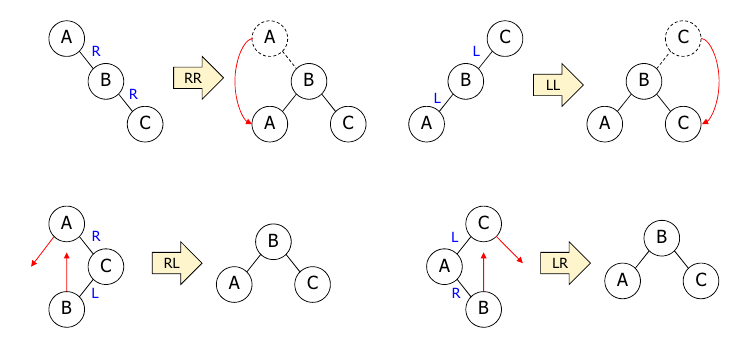
AVL 트리는 각 노드의 왼쪽 서브트리와 오른쪽 서브트리의 높이 차이를 최대한 작게 유지하여 균형을 유지한다. 이를 통해 탐색, 삽입, 삭제 연산에 대해 항상 O(log n)의 시간 복잡도를 유지할 수 있다. AVL 트리는 다음 요소들을 통해 균형을 유지한다.

• Balance Factor : 각 노드의 왼쪽 서브트리의 높이와 오른쪽 서브트리의 높이 차이를 의미한다. 각 노드의 Balance Factor는 -1, 0, 1이어야 한다.
• 회전(Rotation) : 균형을 유지하기 위해 회전 연산을 사용하는데 LL(Left-Left), RR(Right-Right), LR(Left-Right), RL(Right-Left) 회전이 있다. 이러한 회전을 통해 균형을 재조정한다.

레드-블랙 트리(Red-Black Tree)

레드-블랙 트리도 자가 균형 이진 탐색 트리로, 모든 노드는 'Red' or 'Black' 색상을 가지며 루트 노드는 Black이고 빨간색 노드는 연속으로 올 수 없다는 규칙을 만족한다.

1. 모든 노드는 빨강 or 검정이다
2. 루트 노드는 항상 검정이다
3. 모든 null 노드(leaf)는 검정이다
4. 빨강 노드는 연속으로 존재할 수 없다
5. 임의의 노드에서 자손 null 노드로 가는 경로들의 검정 노드 수는 같다 (=black height)

레드-블랙트리는 편향된 이진 탐색트리를 개선한 구조로 rotation과 re-coloring을 통해 균형을 유지하며 최악의 경우에도 O(logn)의 시간복잡도를 가진다. 따라서 실시간 처리처럼 실행시간이 중요한 경우 주로 사용된다.

AVL 트리 vs 레드-블랙 트리

둘 다 자가 균형 이진 탐색 트리이지만, 균형을 잡는 과정에서 레드-블랙 트리에 비해 AVL 트리에서 회전 연산이 더 많이 발생할 수 있다. 레드-블랙 트리는 노드의 색상을 조정하며 균형을 유지하므로 회전이 발생하지 않을 수도 있어 AVL 트리의 균형 조건이 더 엄격한 편이다.

더욱 엄격한 균형 조건의 AVL 트리는 검색 성능이 더 우수할 수 있고 레드-블랙 트리는 삽입/삭제 연산에 더 효율적인 특징을 갖는다.