[논문 리뷰] SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS

태환·2023년 11월 5일
Paper
1

Paper Review

목록 보기
1/15
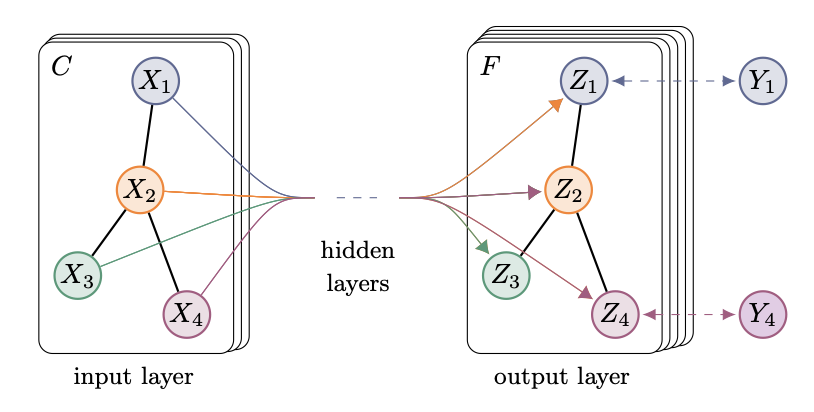
post-thumbnail

📌 SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS

📖 Abstract

해당 논문은 그래프 구조 데이터에 대한 준지도 학습의 확장 가능한 접근 방식을 제시한다.
이 방법은 그래프에 직접 작용하는 효율적인 변형 convolutional neural network을 기반으로 한다.
저자들은 localized first-order proximation of spectral graph convolutions을 통해 convolution architecture 선택의 근거를 제시한다.

📖 Introduction

L=L0+λLregL=L_0 +λL_{reg}

L0L_0는 supervised loss에 해당하며, LregL_{reg}는 graph Laplacian regularization trem으로 저자는 이 부분으로 인해 모델의 성능이 제한된다고 주장한다.

Lreg=∑i,jAij∥f(Xi)−f(Xj)∥2L_{reg} =∑_{i,j}A_{ij}∥f(X_i)−f(X_j)∥^2

즉, 정규화 부분의 ∥f(Xi)−f(Xj)∥∥f(X_i)-f(X_j)∥ 해당 수식으로 인해 연결된 노드는 같은 label을 갖어야한다는 가정이 생기며, 이는 그래프의 엣지가 유사성 이상의 정보를 담을 수 있도록 하는 것을 막아 모델의 성능을 제한한다는 것이 저자의 주장이다.

이를 해결하기 위해 저자는 convolution을 사용하여 정규화 부분을 없애는 것을 목적으로 한다.

Contribution

  1. 해당 논문은 그래프에 직접 작용하는 신경망 모델에 대한 단순하고 잘 동작하는 레이어별 전파 규칙을 제시하고, 이것이 first-order approximation of spectral graph convolutions에서 어떻게 유도될 수 있는지를 보여준다.
  2. 해당 논문은 다음의 그래프 기반 신경망 모델이 그래프 내의 노드를 빠르고 확장 가능하게 준지도 분류하는 데 어떻게 사용될 수 있는지를 보여준다.

📖 Background

1. Convolutional neural network

Convolutional neural network는 다음의 링크에 간략히 정리되어 있다.

2. 기존 그래프 구조에서는 convolution 연산을 적용할 수 없다.


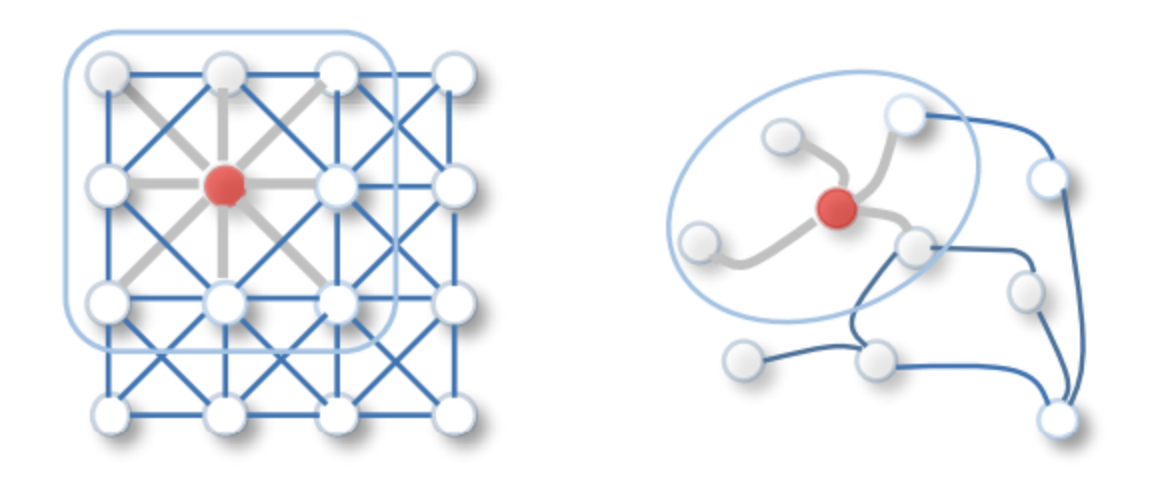
1) convolution 연산은 regular grid에서 사용된다.
그래프 구조는 regular gird 형태가 아니기 때문에 기존 convolution 연산이 불가능하다.
2) filter가 모든 데이터에 대하여 같은 크기가 아니다.
위의 그래프 그림은 빨간 점을 중심으로 1-hop만큼 떨어진 이웃들을 함께 filtering 한 경우이다. 만약 다른 노드를 중심으로 filtering을 진행할 경우 그에 대한 노드의 이웃 수는 달라지게 되며, filter의 크기 또한 달라져야 함을 요구할 것이다.

3. Convolution Theorem을 이용해 convolution 연산을 graph에 적용

Convolution Theorem : 한 도메인의 convolution은 다른 도메인의 point-wise multiplcation과 같다.

F(x∗g)=F(x)⊙F(g)x∗g=F−1(F(x)⊙F(g))F(x*g) = F(x)⊙F(g) \\x * g = F^{-1}(F(x) ⊙ F(g))\\
xx : signal (그래프에서는 node feature가 해당된다.)
gg : filter

즉 우리는 기존 도메인에서 다른 도메인으로 graph를 변환하면 convolution 연산 대신 point-wise multiplication 연산을 통해 동일한 결과를 만들 수 있다는 것이다.

위의 수식을 보면 F(⋅)는 도메인을 변환해주는 함수이기에 입력 신호와 filter를 다른 도메인으로 변환시켜준 뒤 point-wise mutiplication 연산을 진행한 후 다시 기존의 도메인으로 변환해주면 convolution 연산과 동일한 것을 알 수 있다.

4. Fourier Transform을 이용한 graph 도메인 변환

Fourier Transform : 신호를 주파수 도메인으로 변환하는 수학적 도구 중 하나이다.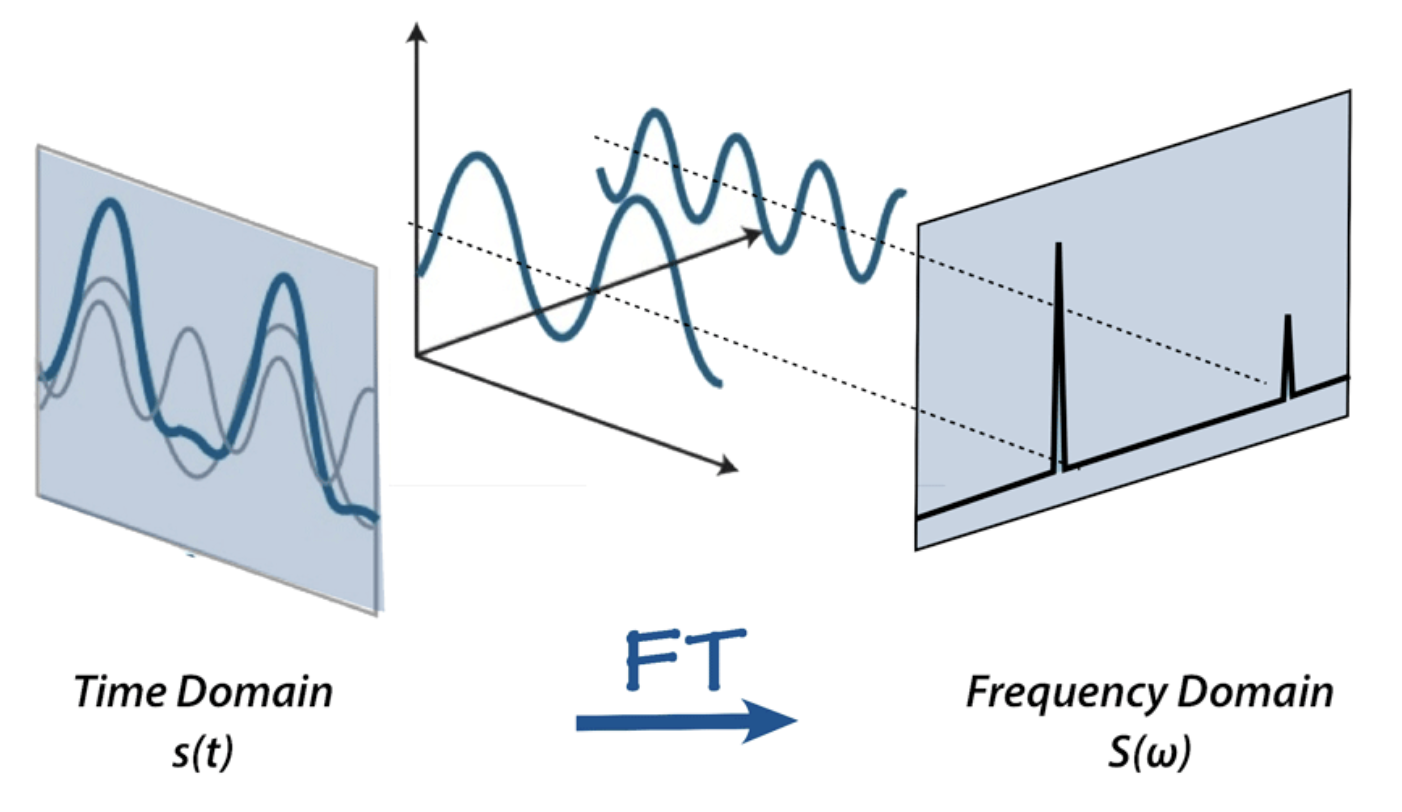


Fourier Transform을 graph에 적용하여 spatial 구조에서 spectral 구조로 변환하여 point-wise multiplication 연산을 진행한 후 다시 spatial 구조로 되돌려 convolution 연산과 동일한 결과를 만드는 것이 목적이다.

다음의 그림은 Fourier Transform을 그래프에 적용한 모습이다.
우리가 알고있는 기존의 그래프 구조를 Spatial 구조라고 부르며,
위에서 언급한 Fourier Transform을 적용하여 아래의 주파수 도메인 즉, Spectral 구조로 변환했다.

5. Laplacian Matrix

위에서 언급한 일련의 과정은 Laplacian Matrix 연산과 같다고 한다.
Laplacian Matrix가 무엇인지 알아본 뒤,위에서 거친 과정의 수식을 최종적으로 나타내고자 한다.

Laplacian Matrix : Degree Matrix - adjacency matrix로 정의된다.
Degree Matrix : 한 노드에 연결된 링크의 개수를 대각선에 표현한 행렬
Adjacency matrix : i노드와 j노드 사이에 link가 있는 경우 1, 없는 경우 0으로 채워진 행렬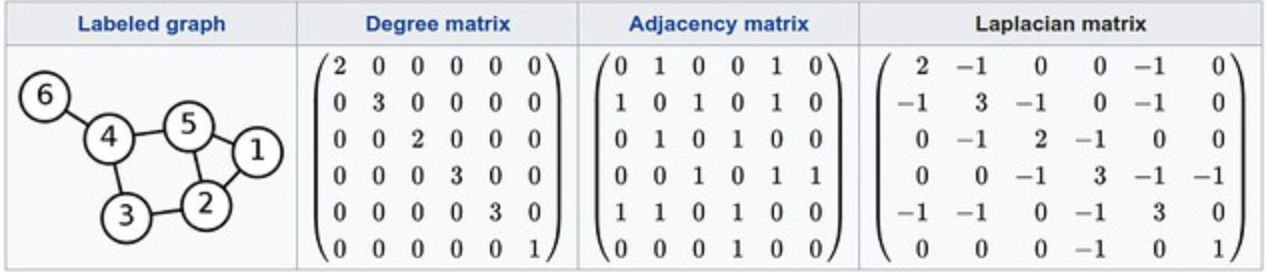


Laplacian Matrix은 Degree Matrix와 Adjacency Matrix의 차로 이루어졌지만,
사실 차가 내포하는 의미는 없고 단지 두 행렬이 합쳐져 다음의 특징을 지닌다.
1. 몇개의 노드와 연결이 되었는가 (Adjacency Matrix의 특징)
2. 어떤 노드와 연결이 되었는가 (Degree Matrix의 특징)

추가적으로 Normalized Laplacian matrix는 다음과 같다.

L=IN−D−21AD−21=U⋀UTL = I_N - D^{-2\over1}AD^{-2\over1} = U⋀U^T

Laplacian Matrix는 대각성분을 기준으로 좌우가 대칭이며, 대각성분이 모두 양수이기 때문에 eigen decomposition이 가능하다.
따라서 Laplacian Matrix를 eigen decomposition하면 다음과 같이 표현할 수 있다.

L=UgθUTL = Ug_θU^T\\
LL : normalized graph Laplacian
UU : the matrix of eigenvectors of L = Fourier basis vector
gθg_θ : function of the eigenvalues of L = filter

이를 Fouriere Transform을 이용한 과정과 같다고 두면 다음과 같다.

x ∗ g=F−1(F(x)⊙F(g))=UgθUTxx\,∗\,g=F^{−1}(F(x)⊙F(g)) = Ug_θU^Tx

논문에서는 다음의 식을 통해 저자의 주장을 전개해 나아간다.

수학적인 배경지식을 많이 요구하여 이해하는데 어려움이 있지만, 도움이 되는 다양한 자료를 찾아보면 감이 잡힐 것이다.

📖 Fast Approximate Convolutions on graphs

1. Spectral Graph Convolutions

gθ∗x=UgθUTxg_θ * x = Ug_θU^Tx

위의 식은 많은 계산량을 필요로 한다는 한계점이 있다.
1. eigen vector matrix U와의 곱셈 연산은 계산에 많은 시간이 걸린다.
2. large graph에 대한 L의 eigen decomposition 계산은 비용이 많이들 수 있다.

이를 해결하기 Chebyshev polnomials을 사용하면 K차 까지의 절단된 전개로 잘 근사할 수 있다고 제안한다.
(K의 범위는 직접 지정할 수 있으며, 해당 논문에서는 1로 지정한다.)

gθ′(⋀)≈∑k=0Kθk′Tk(⋀′),g_{θ'}(⋀)≈∑_{k=0}^{K}θ'_kT_k(⋀'),\\
⋀′=2λmax⋀−IN,λmax⋀' = {2\over λ_{max}}⋀-I_N, λ_{max} denotes the largest eigenvalue of L
θ′∈RKθ' ∈ R^K is now a vector of Chebyshev coefficients

Chebyshe polynomials은 재귀적으로 정의되며, T0(x)=1T_0(x) = 1, T1(x)=xT_1(x) = x 초기값과 함께 Tk(x)=2xTk−1(x)−Tk−2(x)T_k(x) = 2xT_{k-1}(x) - T_{k-2}(x)를 사용하여 계산된다.

즉, eigendecomposition 된 normalized graph Laplacian Matrix를 localized 하기 위해 Chebyshev 다항식으로 변환한 것이다.
이를 신호 xx와 필터 gθ′g_{θ'}의 convolution 정의로 되돌아가면 다음과 같이 나타낼 수 있다.

gθ′∗x≈∑k=0Kθk′Tk(L′)xg_{θ'}*x≈∑_{k=0}^{K}θ'_kT_k(L')x\\
L′=2λmaxL−IN,L' = {2\over λ_{max}}L-I_N,\\이는 (U⋀UT)k=U⋀kUT(U⋀U^T)^k = U⋀^kU^T인 사실임을 고려함으로써 확인할 수 있다.

해당 식은 k-localized된 식으로 eigen vector maxtrix U와의 곱셈 연산은 계산에 많은 시간이 걸린다는 문제를 해결했다.
즉, 이것은 Laplacian의 K차 다항식으로 표현되어 중심 노드로부터 최대 K 단계 떨어진 노드에만 의존하는 것을 의미한다.

2. Layer-Wise Linear Model

그래프 합성곱을 기반으로하는 신경망 모델은 위 식의 형태를 다중 합성곱 층으로 쌓음으로써 만들 수 있다.
추가적으로 저자는 몇가지의 작업을 통해 수식을 개선한다.
1. K를 1로 설정함으로써 레이어가 단일 step의 이웃 노드에만 영향을 미치고 더 멀리 떨어진 노드에 대한 정보는 고려하지 않도록 만든다.
2. GCN의 선형 형식에서 λmaxλ_{max}를 2로 근사화함으로써 위의 식을 단순화한다.
위의 두 과정을 고려하면 식은 다음과 같다.

gθ′∗x≈θ0′x+θ1′(L−IN)x=θ0′x−θ1′D−21AD−21xg_{θ'}*x≈θ'_0x + θ'_1(L-I_N)x = θ'_0x−θ'_1D^{−2\over1}AD^{-2\over1} x

이 필터 매개변수 θ0′θ'_0와 θ1′θ'_1는 전체 그래프에 대해 공유할 수 있으며, 과적합을 해결하고 각 레이어에서 수행되는 연산의 수를 최소화하기 위해 파리미터의 수를 제한하는 것이 유용할 수 있다.

gθ′∗x≈θ(IN+D−21AD−21)x,g_{θ'}*x≈ θ(I_N + D^{−2\over1}AD^{-2\over1})x,\\
parameter θ=θ0′=−θ1′θ = θ'_0 = -θ_1'

이를 반복적으로 적용하면 심층 신경망 심층 신경망 모델에서 수치적 불안정성과 기울기 폭주/소멸 문제가 야기될 수 있기 때문에 저자는 다음과 같은 정규화 트릭을 사용한다.

IN+D−21AD−21−>D′−21A′D′−21I_N + D^{−2\over1}AD^{-2\over1} -> D'^{−2\over1}A'D'^{-2\over1}\\
A′=A+INA' = A + I_N
Dij′=∑jAij′D'_{ij} = ∑_jA'_{ij}

이를 통해 그래프 신경망 모델에서 더 나은 수치 안정성을 달성할 수 있으며, 심층 신경망에서 발생할 수 있는 문제들을 완화할 수 있다고 한다.
최종적인 수식은 다음과 같다.

Z=D′−21A′D′−21XΘZ = D'^{−2\over1}A'D'^{-2\over1}XΘ\\
X∈RN×CX∈R^{N×C} : 입력 신호 (C는 모든 노드의 feature dimension)
Θ∈RN×FΘ∈R^{N×F} : filter 파라미터의 매트릭스
Z∈RN×FZ∈R^{N×F} : convolved signal matrix

📖 Semi-supervised node classification

최종적으로 해당 논문의 순방향 모델은 다음과 같은 형태이다.

Z=f(X,A)=softmax(A^ReLU(A^XW(0))W1)Z = f(X,A) = softmax(Â ReLU(ÂXW^{(0)})W^{1})\\
A^=D′−21A′D′−21Â = D'^{−2\over1}A'D'^{-2\over1}

저자는 Semi-supervised 다중 클래스 분류를 위한 loss 함수로 모든 레이블이 지정된 데이터에 대해 교차 엔트로피 오차를 평가함으로써 처음에 언급한 정규환된 부분을 제거했다.

𝓛 = −∑l∈YL∑f=1FYlf-∑_{l∈Y_L}∑^F_{f=1}Y_{lf}lnZlfZ_{lf}\\
YL:Y_L : label을 가지는 set of node

📖 Experiments

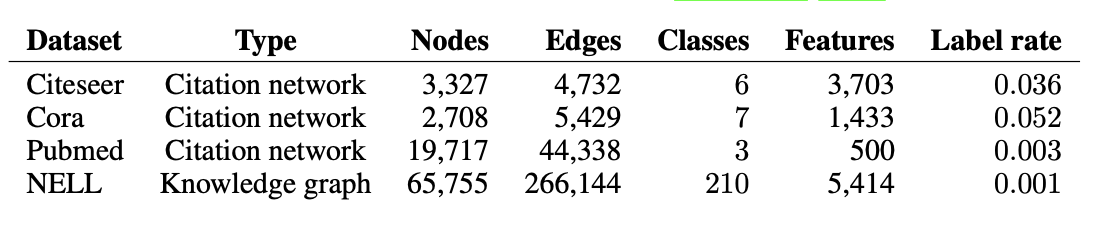
저자는 다음의 데이터셋을 대상으로 실험을 진행했다.

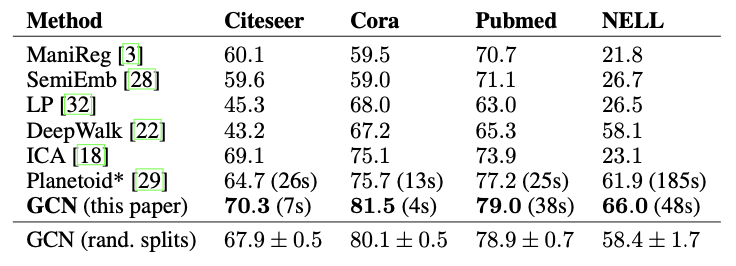
실험 결과는 다음과 같다.
해당 모델은 다른 Method들에 비해 모든 데이터에서 높은 성능을 보였다.

추가적으로 저자는 각 레이어 별 전파 모델의 다른 변형을 비교한다.

📖 Discussion

  1. 메모리 요구량 : 해당 논문에서는 full-batch 경사하강법을 사용하지만, 대규모의 데이터 집합의 경우 메모리 요구량이 높아질 수 있는 문제가 있기 때문에 mini-batch 확률적 경사하강법이 연구되어야한다.
  2. 방향성 있는 edge와 edge feature : 해당 논문에서는 edge의 특성을 반영하지 않으며, 방향성이 없는 그래프로 제한한다. 따라서 방향성이 있는 그래프와 edge의 특징을 반영하는 그래프에 대해서도 연구되어야한다.
  3. 한계적인 가정 : 해당 논문에서는 이웃 노드의 연결 가중치와 자신 스스로의 연결 가중치를 동일하게 적용한다. 추가적으로 파라미터를 도입해서 가중치를 다르게 부여하는 것이 연구되어야 한다.

📖 Conclusion

해당 논문은 그래프에서 Spectral convolution의 first-order approximation을 기반으로한 효율적인 계층별 전파 규칙을 사용하여 그래프 구조 데이터에 대한 준지도 학습 분류 방법을 소개했다.

Reference

  1. SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS
  2. [Paper Review] Semi-supervised Classification with Graph Convolutional Networks
  3. [Open DMQA Seminar] Graph Neural Networks: Introduction to Spectral Graph Convolution

코드

GCN 코드 구현

profile
태환
연세대학교 컴퓨터과학과 석사 과정
다음 포스트

[논문 리뷰] Neural Collaborative Filtering

0개의 댓글