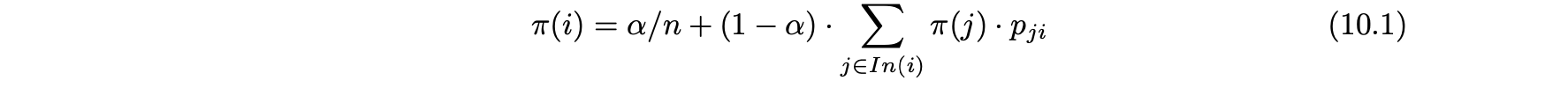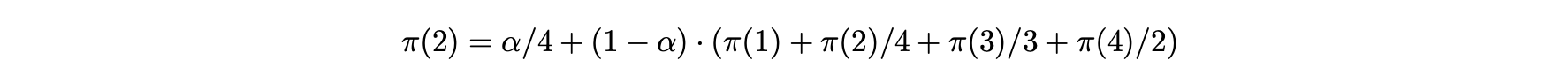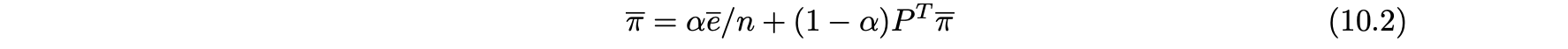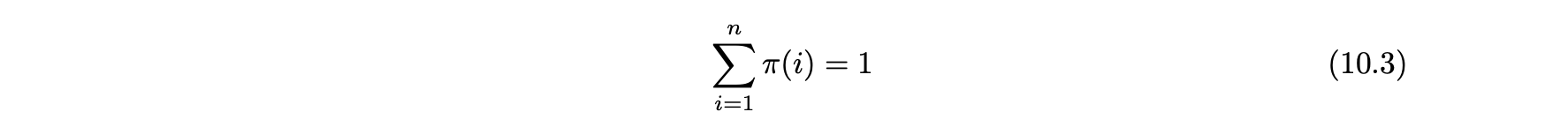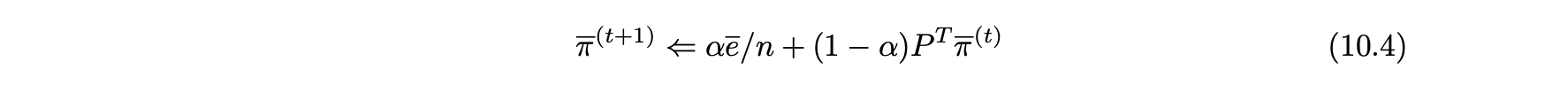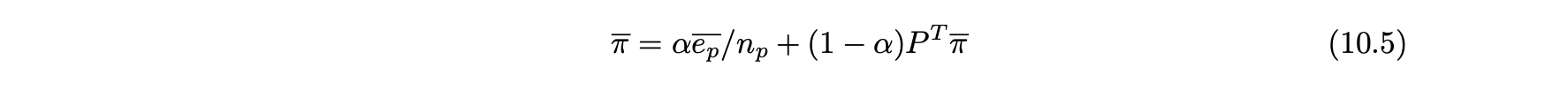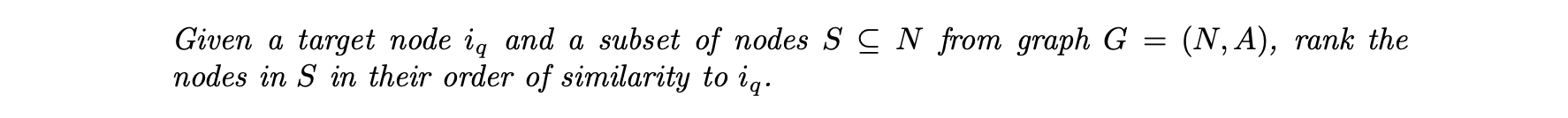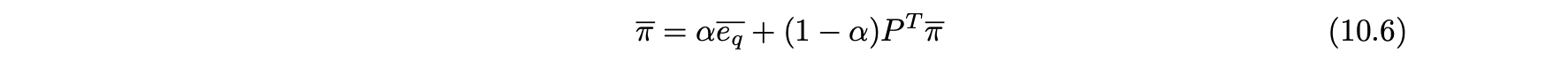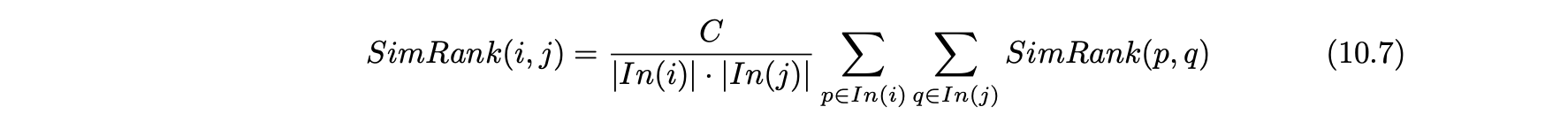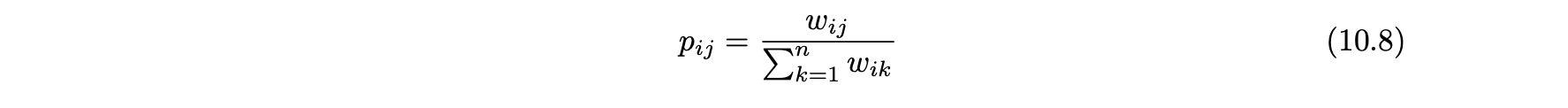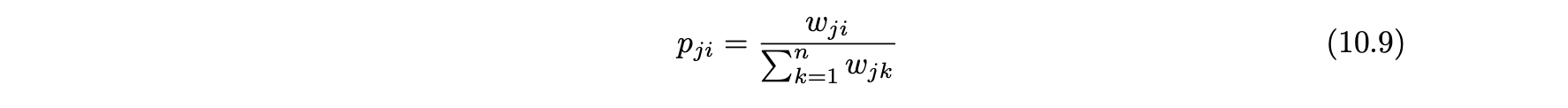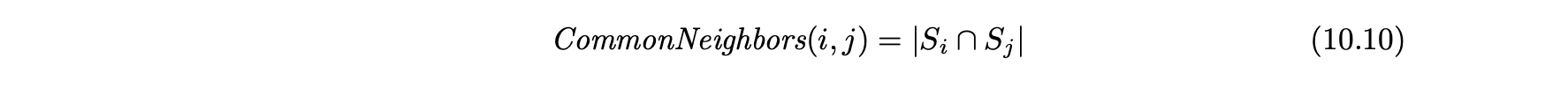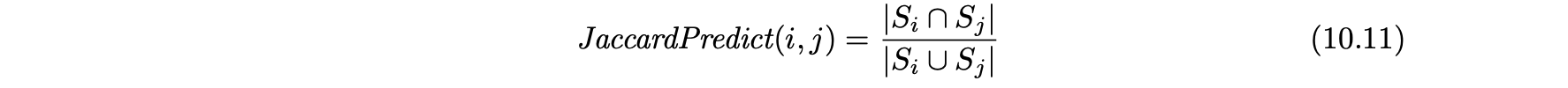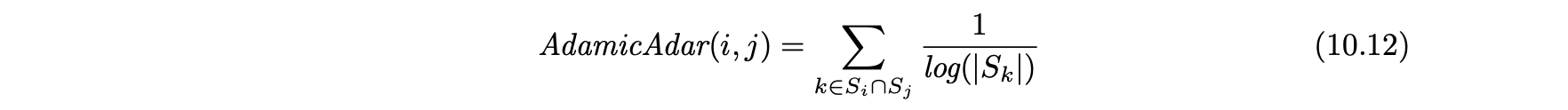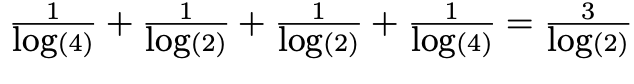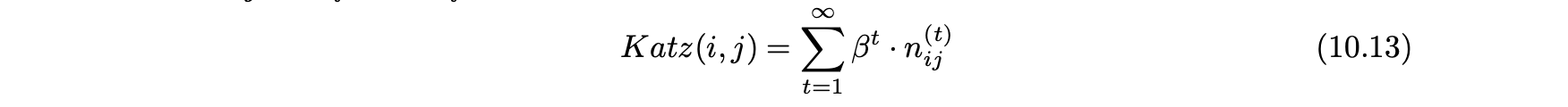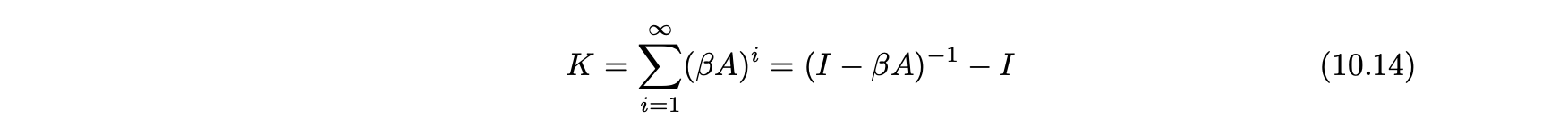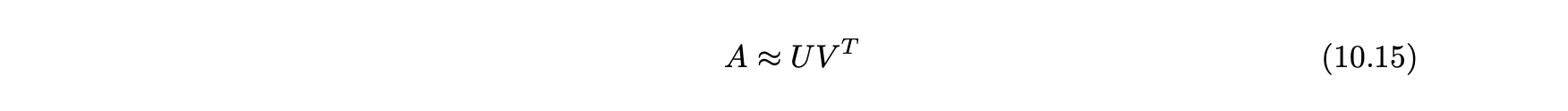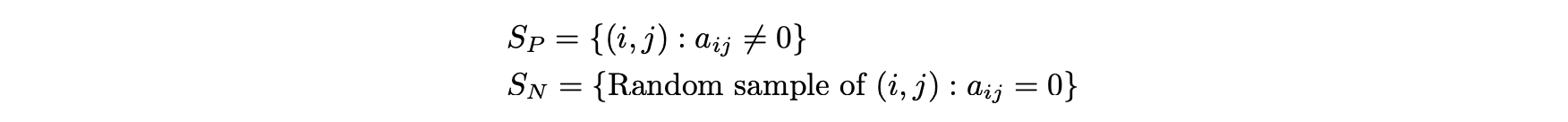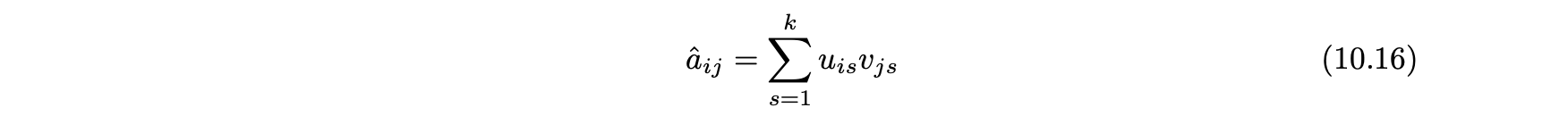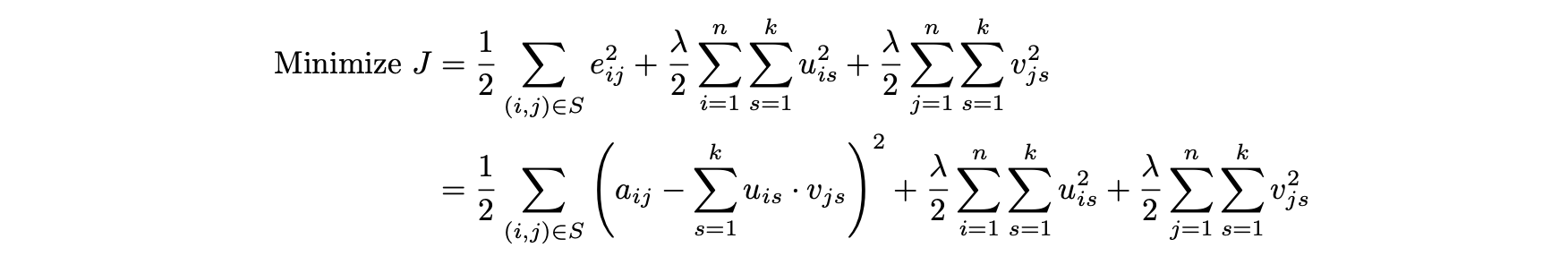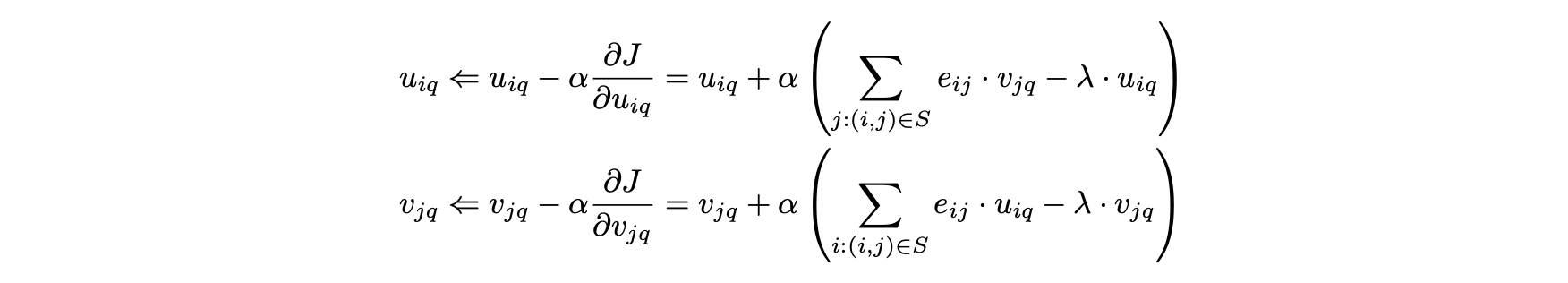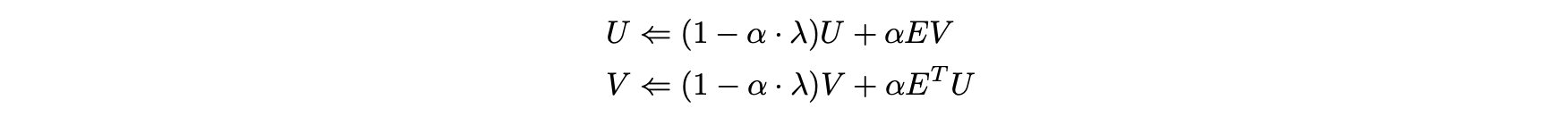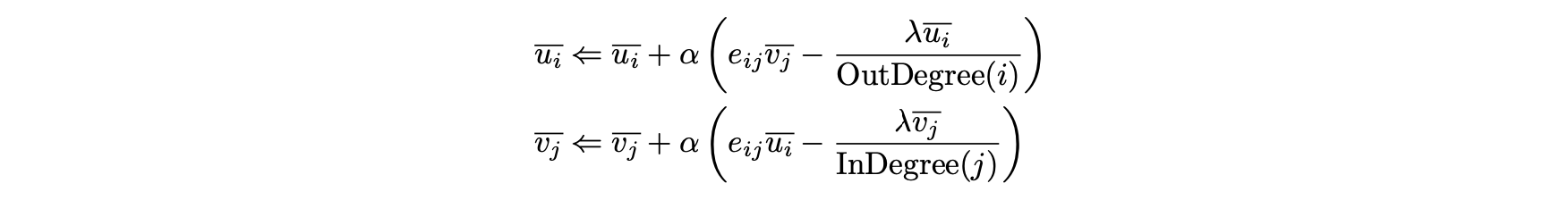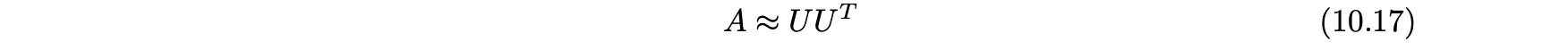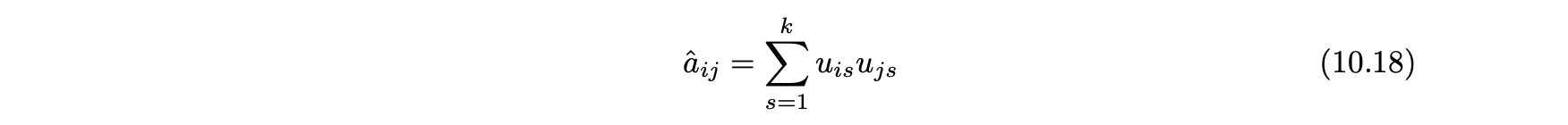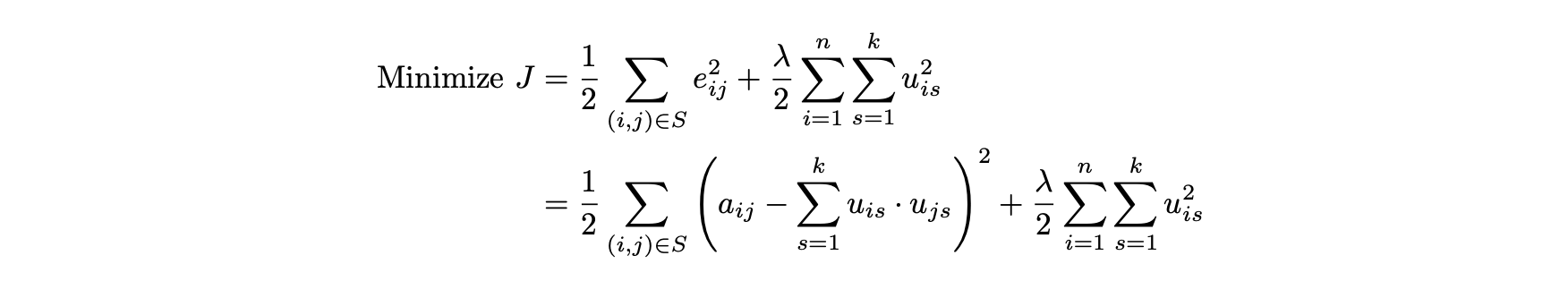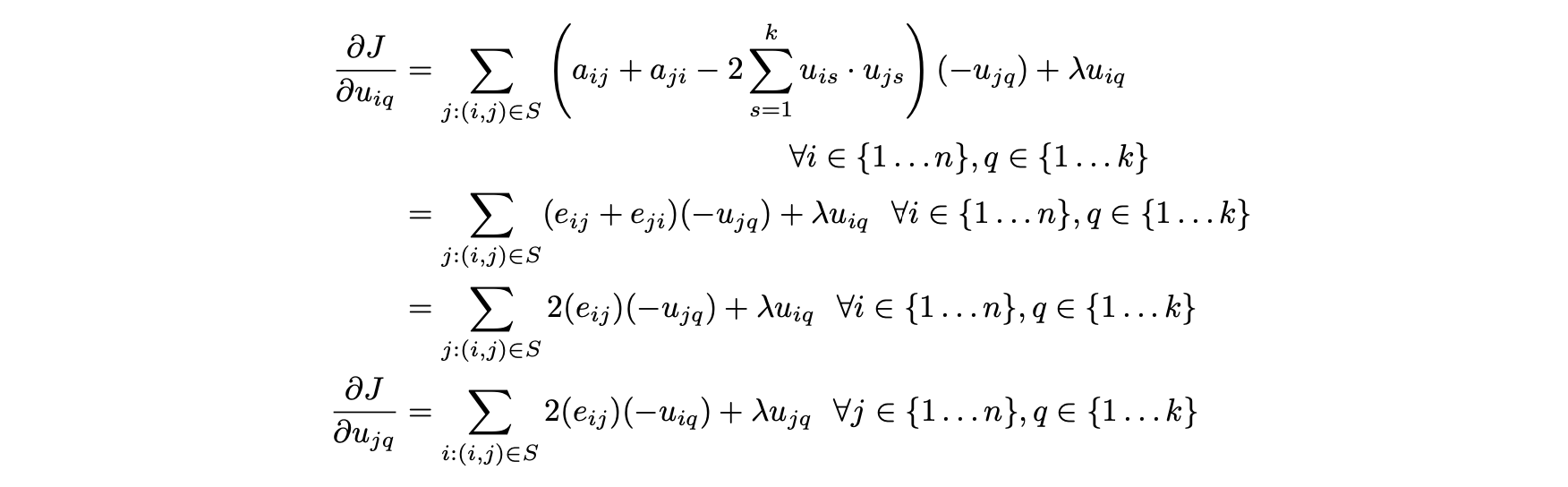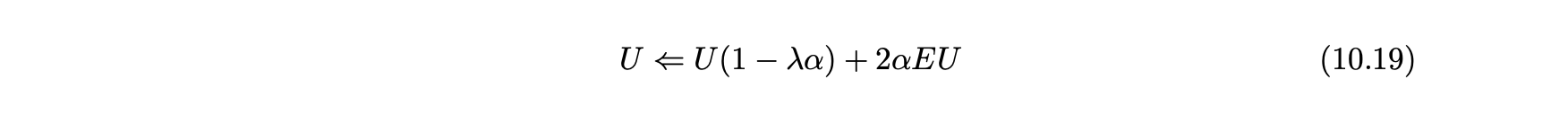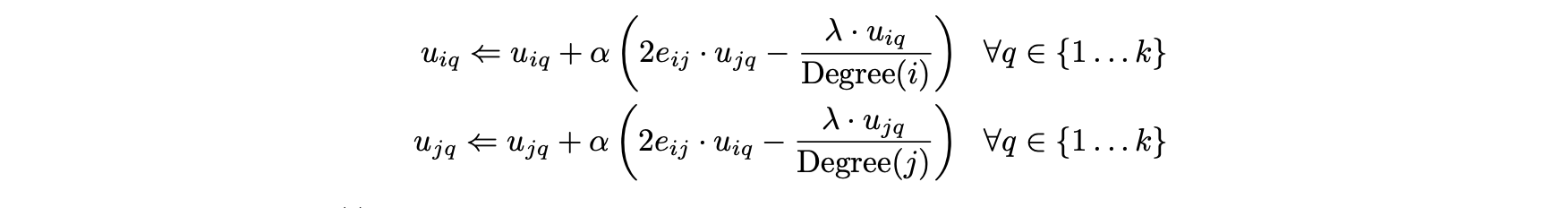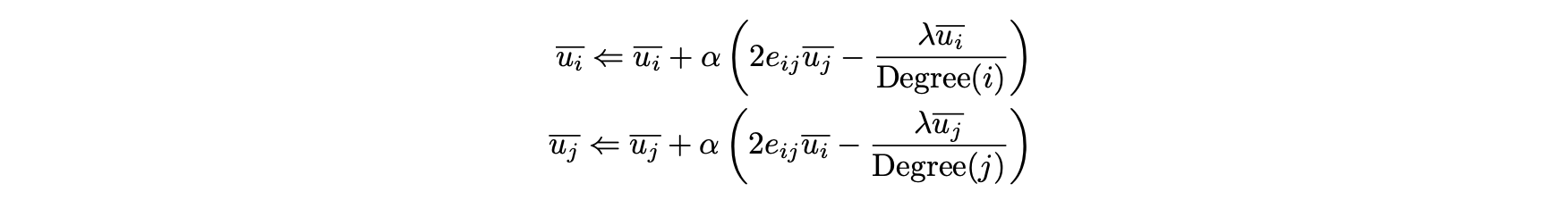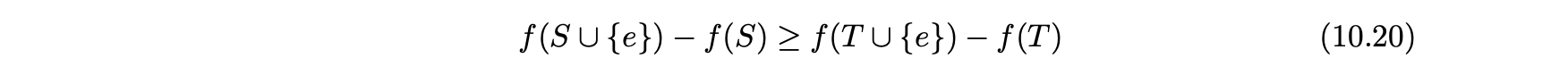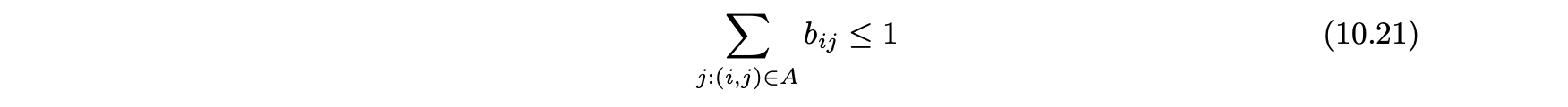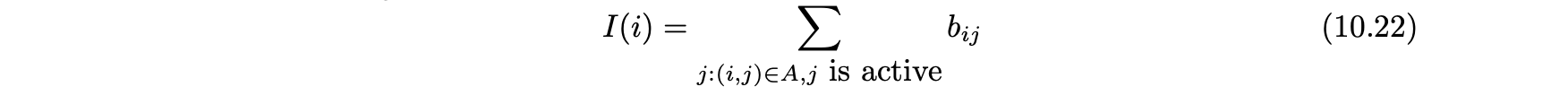📌 개요

• 네트워크는 소셜 및 정보 네트워크와 같은 많은 애플리케이션에서 모델링 도구로 어디서나 볼 수 있게 됐다.
• 각기 다른 유형의 구조 추천 사항은 서로 다른 시나리오에서 서로 다른 애플리케이션 세트를 가질 수 있다.

다양한 변형의 주요 예는 다음과 같다.

1. 권한 및 컨텍스트별 노드 추천 : 노드의 품질은 들어오는 링크로 판단되며 노드의 개인별 관련성은 해당 컨텍스트로 판단된다.
2. 예제별 노드 추천 : 많은 추천 애플리케이션에서 다른 예제 노드와 유사한 노드를 추천할 수 있다.
3. 영향 및 콘텐츠별 노드 추천 : 많은 웹 중심 애플리케이션에서 사용자는 다양한 유형의 제품에 대한 지식을 전파할 수 있으며 이 문제를 바이럴 마케팅이라고 한다.
4. 추천 링크 : 페이스북과 같은 많은 소셜 네트워크에서 네트워크의 연결성을 높이는 것이 소셜 네트워크의 관심 대상이며, 사용자는 종종 잠재적인 친구를 추천 받는다.

• 이러한 구조적 추천 방법은 웹 중심 네트워크로 모델링할 수 있는 모든 시스템의 쇼오를 추천하는 데 사용할 수 있다.
• 전통적인 제품 추천 문제조차도 이러한 방법으로 해결될 수 있다.
  • 사용자 제품 추천 문제는 사용자 항목 그래프로 모델링할 수 있다.

📌 순위 알고리듬

• 페이지 랭크 알고리듬은 웹 검색 맥락에서 처음 제안됐다.
• 웹 페이지의 평판과 품질을 결정하는 메커니즘이 필요했으며, 이는 웹의 인용 구조를 사용해 달성했다.
• 인-랭크 페이지의 수는 품질의 대략적인 지표로 사용될 수 있지만, 가리키는 페이지의 품질을 고려하지 않기 때문에 완전한 결과를 제공할 수 없어 더욱 전체적인 인용 기반 투표를 제공하기 위해 페이지 랭크라고 하는 알고리듬이 사용된다.
  • 페이지 랭크 알고리듬은 직접 추천 방법은 아니지만 추천 사항 분석 주제와 밀접한 관련이 있다.
  • 페이지 랭크의 많은 변형이 개인별 랭킹 메커니즘에 사용된다.

📖 페이지 랭크

• 페이지랭크 알고리듬은 웹 그래프에서 인용 구조를 사용해 노드의 중요성을 모델링한다.
• 노드는 웹 페이지에 해당하며 선은 하이퍼링크에 해당한다.
• 기본 개념은 평판이 좋은 문서가 다른 평판이 좋은 웹 페이지에 의해 인용되거나 연결될 가능성이 높다는 것이다.
• 웹 그래프에서 무작위 서퍼 모델을 사용해 페이지 랭킹 목표를 달성하기 위해 사용된다.
• 페이지 랭크 알고리듬은 임의 서퍼의 장기 방문 빈도 측면에서 웹 페이지의 평판을 모델링한다.
  • 이 장기 빈도는 정상 상태 확률이라고도 하며 모델을 랜덤 워크 모델이라고도 한다.
• 중요한 문제는 일부 웹 페이지에 발신 링크가 없을 수 있으며, 임의의 서퍼가 특정 노드에 갇힐 수 있다는 것이다.
  • 이러한 노드를 데드-엔드라고 한다.
  • 데드-엔드 노드의 예는 그림 10.1(a)에 설명돼 있다.
    

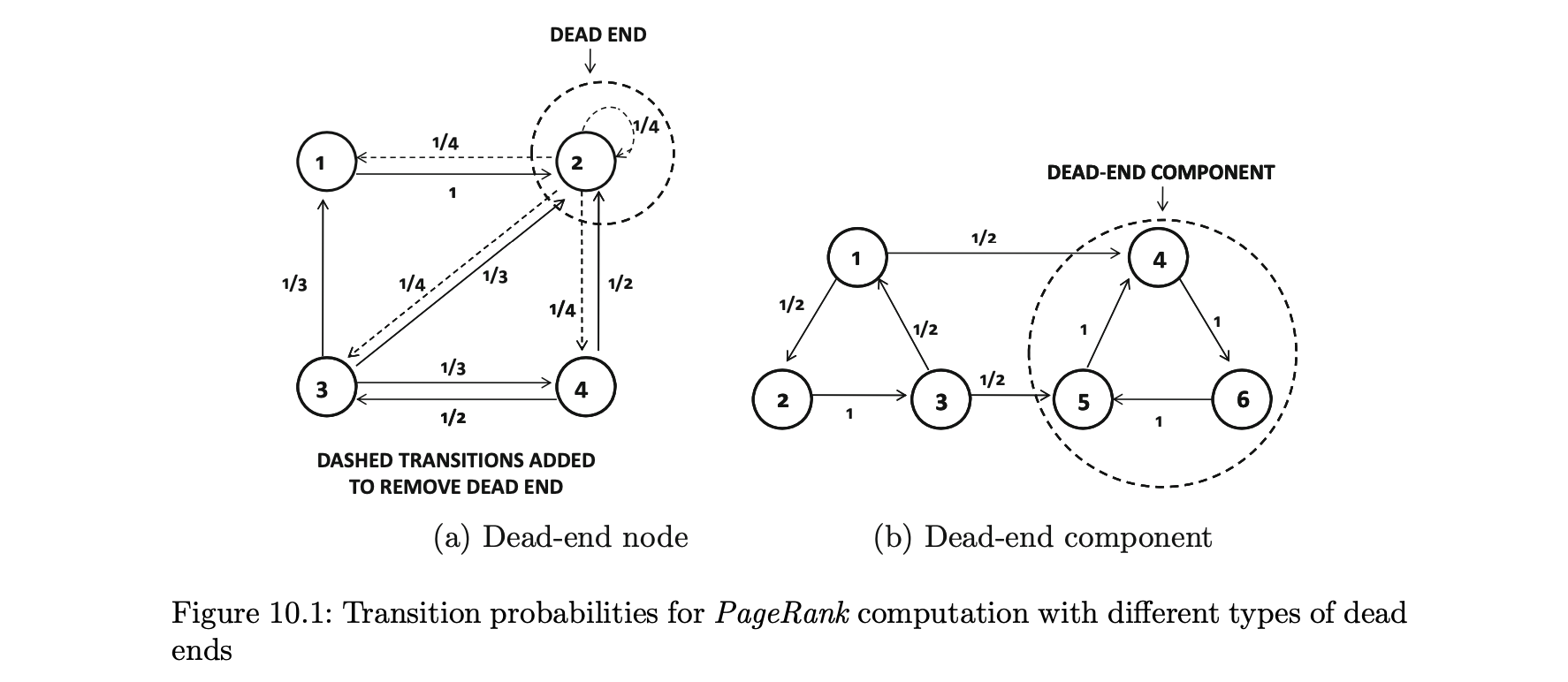
문제를 해결하기 위해 두 가지 수정 사항이 랜덤 서퍼 모델에 통합됐다.

1. 자체 루프를 포함해 데드-엔드 노드에서 모든 노드로 연결되는 링크를 추가하는 것이다.
   • 이러한 각 선은 1/n의 전이 확률을 갖는다.
   • 노드 그룹에서 데드-엔드를 정의할 수도 있기 때문에 이 문제는 완전히 해결되지 않는다.
   • 그림 10.1(b)는 데드-엔드의 구성 요소의 예시를 제공한다.
   • 웹은 강하게 연결돼 있지 않기 때문에 웹 그래프에서 데드-엔드 구성 요소가 일반적이다.
2. 임의의 서퍼 모델 내에서 순간 이동 또는 재시작 단계가 사용된다.
   • 각각의 전이에서 랜덤 서퍼는 확률이 α인 임의의 페이지로 점프하거나, 확률 (1-α)이 있는 페이지의 링크 중 하나를 따를 수 있다.
   • 사용되는 α의 일반적인 값은 0.1이다.
   • α 값이 크면 일반적으로 다른 페이지가 더 균등해질 수 있는 정상 상태 확률이 초래된다.
   • 정상 상태에서 노드 i로의 전이 확률은 순간 이동 및 전이 사건의 확률의 합으로 정의된다.
     
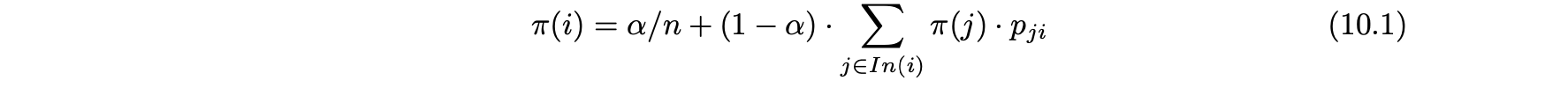
     • 그림 10.1(a)의 노드 2에 대한 방정식은 다음과 같이 쓸 수 있다.
       
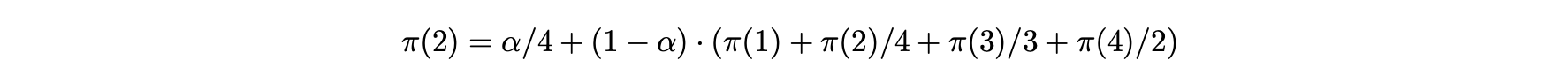
   • 각 노드마다 그런 방정식이 하나씩 있으므로 전체 방정식은 시스템을 행렬 형태로 작성하는 것이 편리하다.
   • 방정식 시스템은 다음과 같이 행렬 형식으로 다시 작성할 수 있다.
     
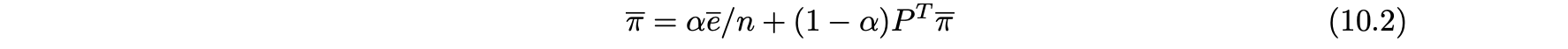
     • 오른쪽의 첫 번째 용어는 순간 이동에 해당하고 두 번째 용어는 인-링크 노드에서 직접 전이에 해당한다.
   • 벡터 π는 확률을 나타내므로 성분의 합은 1과 같아야 한다.
     
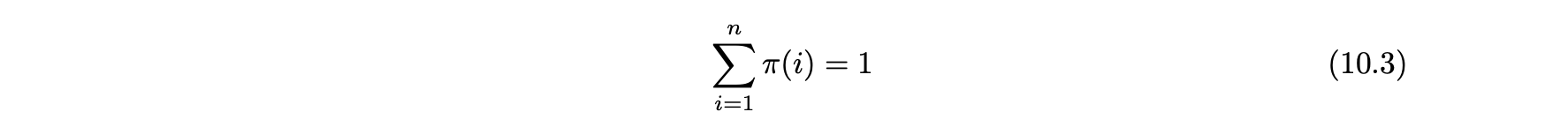
   • 알고리듬은 벡터 π를 초기화해 시작하고 다음과 같은 반복 단계를 통해 결과를 도출한다.
     

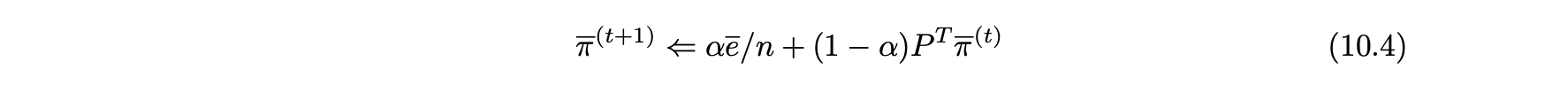
📖 개인화된 페이지 랭크

• 개인화된 페이지 랭크의 개념은 인기 있는 노드를 찾도록 설계됐으며 이는 네트워크의 특정 노드와 유사하다.
• 핵심은 순간 이동 메커니즘이 특정 노드를 향해 랜덤-워크를 바이어스시키는 방법을 제공한다는 것이다.
• 일반적으로 사용자는 다른 주제보다 특정 주제 조합에 더 관심이 있을 수 있으며, 이러한 관심사에 대한 지식은 사용자 등록으로 인해 개인화된 검색 엔진에 제공될 수 있다.

사용자가 특정 주제에 대한 관심을 표현할 수 있는 웹 추천 시스템 고려하기

• 첫 번째 단계는 기본 주제 목록을 수정하고 각 주제에서 고품질의 페이지 샘플을 결정하는 것이다.
• 페이지 랭크 방정식이 수정돼 순간 이동은 웹 문서의 전체 공간이 아니라 이 웹 문서의 샘플 세트에서만 수행된다.
• 페이지 랭크 방정식 10.2를 다음과 같이 수정할 수 있다.
  
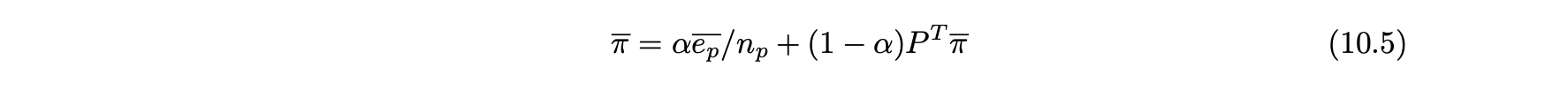
  • ep는 각 페이지마다 하나의 항목이 있는 n 차원 개인화 벡터가 되도록 하며, 해당 페이지가 샘플 세트에 포함되면 ep는 1의 값을 취하고 그렇지 않으면 0을 사용한다.
  • ep의 0이 아닌 항목 수를 np로 표시한다.

📖 이웃 기반 방법에 대한 응용

• 개인화된 페이지 랭크 방법의 순간 이동 메커니즘은 재시작이 실행되는 노드에 구조적으로 더 가까운 노드의 순위를 증가시킨다는 점이 주목할 만하다.
• 개인화된 페이지 랭크 알고리듬을 사용하면 반환된 이웃의 인용 순위 측면에서도 품질이 향상된다.
• 이웃 발견에 대한 기본적인 쿼리는 다음과 같다.
  
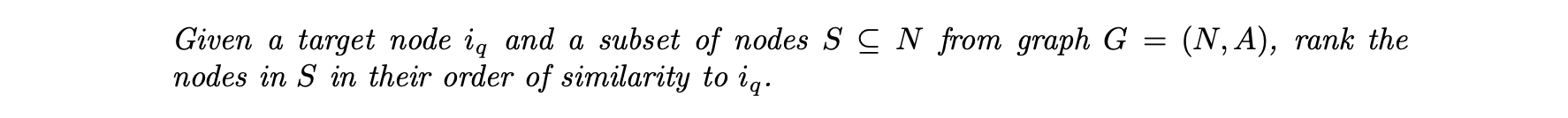
  • 노드가 사용자 및 아이템에 대응하고 에지가 선호에 대응하는 양방향 선호도 그래프 형태로 사용자 및 아이템이 배열되는 추천 시스템에서 매우 유용하다.
• 이 문제는 주제에 민감한 페이지 랭크의 제한적인 사례로 볼 수 있으며,
  여기서 단일 노드 iq로 순간이동이 수행된다.
  따라서 개인화된 페이지 랭크 방정식 10.5는 노드 iq에 대응하는 순간 이동 벡터 즉 노드 iq에 대응하는 단일 1을 제외한 모든 0의 벡터를 사용해 직접 조정할 수 있다.
  
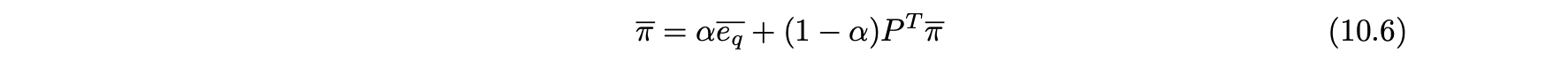
  • 이 유사도의 정의는 쿼리 노드 i에서 시작하는 노드 j에 할당된 유사도 값이 쿼리 노드 j에서 시작하는 노드 i에 할당된 유사도 값과 다르기 때문에 비대칭이다.
  • 이러한 비대칭 유사도 측정은 검색 엔진 및 추천 시스템과 같은 쿼리 중심 애플리케이션에 적합하다.
  • 전형적인 협업 필터링 애플리케이션에서, 타깃 사용자 또는 아이템의 이웃을 결정하려고 시도하기 때문에 이러한 이웃이 발견된 후 이들 노드의 콘텐츠 특성을 기반으로 추천 사항을 작성하는 데 사용할 수 있다.

1. 소셜 네트워크 추천

• 기본 네트워크는 사용자가 명시적으로 지정된 관심사를 갖는 소셜 네트워크의 경우를 고려하고, 링크는 우정 관계를 나타낸다.
• 그러한 경우 추천의 목적을 위해 사용자의 이웃 프로필을 이용하는 것이 바람직할 수 있다.
• 사용자의 이웃은 소셜 네트워크에서 해당 사용자 노드에서 제시작되는 개인화된 페이지 랭크 알고리듬을 사용해 찾을 수 있다.
• 주변의 소셜 프로필은 지정된 키워드, 좋아요 또는 명시적으로 지정된 평점으로 검색할 수 있다.
• 대상 노드 주변의 소셜 프로필과 일을 집계할 수 있으며 이러한 프로파일에서 가장 좋아하는 항목을 대상에 추천할 수 있다.
• 따라서 이 접근법은 구조적 데이터가 이웃을 결정하지만 사용자가 지정한 관심 사항이 최종 추천을 하는 데 사용되는 하이브리드 추천 시스템의 유형으로 볼 수 있다.
  • 이 접근 법은 소셜 네트워크에서 동질성 개념을 활용한다.
  • 기본 아이디어는 소셜 네트워크의 연결된 사용자가 종종 유사한 속성을 가지고 있다는 것이다.
  • 따라서 사용자 주변의 속성, 프로필 및 평점을 활용해 추천할 수 있다.
• 이 문제는 집단 분류의 문제와 관련이 있다.
  • 집단적 분류에서 머신러닝 모델을 사용해 동일한 목표를 달성할 수 있다.
  • 사전 지정된 노드는 집단 분류 알고리듬의 학습 데이터다.

2. 이종 소셜 미디어의 개인화

• 이기종 소셜 미디어에서 동일한 네트워크에는 사용자, 미디어 컨텐츠 및 텍스트 설명이 포함될 수 있다.
• 텍스트, 사용자 및 이미지가 있는 이기종 소셜 네트워크의 개념 설명이 그림 10.2에 나와 있다.
  
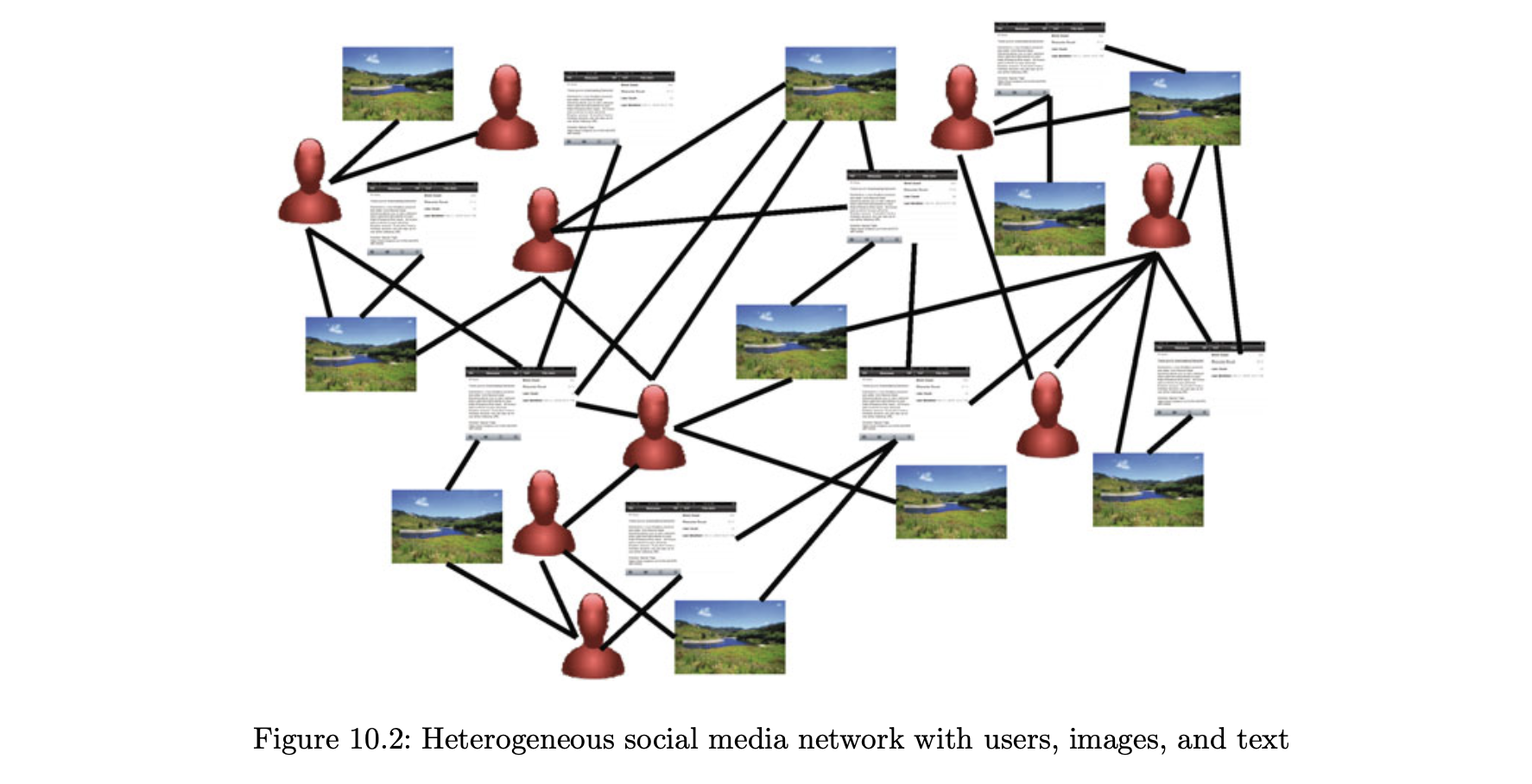
  • 주요 아이디어는 고품질 사용자와 콘텐츠가 네트워크 구조 내에서 자연스럽게 연결돼 있다는 것이다.
  • 이 개념은 페이지 랭크 알고리듬에서 사용하는 원리와 유사하다.
  • 기본 링크 구조의 상호보강적인 특성을 사용함으로써 관련 사용자 및 콘텐츠를 동시에 발견할 수 있으며, 동시에 결과는 사용자나 쿼리에 맞게 조정될 수 있으므로 개인화된 랭킹 방법을 사용해야 한다.
• 이기종 네트워크에서 접근 방식을 사용할 때의 주요 과제는 네트워크의 특정 양식이 상당히 많은 수의 노드가 있는 경우 전체 순위 과정을 압도적으로 지배할 수 있다는 것이다.
• 따라서 각 양식이 다른 양식으로부터 힌트를 얻는 방식으로 랭킹 과정을 수행하는 것이 중요하지만 각 객체 평점에 대한 랭킹 과정은 별도로 유지된다.
• 따라서 반복적 접근법이 사용되는데, 여기서 각 양식 내에서 별도의 순위 과정이 수행되고, 다른 양식으로부터의 순위가 각 양식에서 다음 반복에서 유사도 행렬을 수정하는데 사용된다.
• 따라서 접근 방식은 각 양식 내에서 노드-노드 유사도 행렬을 구성하는 것으로 시작해 수렴할 때까지 다음 2단계 반복 과정을 사용한다.

1. 각 양식 내의 유사도 행렬에서 페이지랭크를 별도로 사용해 각 노드에 대한 순위를 작성한다.
2. 순위를 사용해 유사도 행렬을 재조정한다.
한 쌍의 노드가 동일한 노드에 연결되거나 다른 양식에서 높은 순위의 상호 연결성이 높은 노드에 연결되면 노드 간의 유사도가 증가한다.

3. 전통적인 협업 필터링

• 개인화된 페이지 랭크 접근 방식 또한 기존 협업 필터링 어플리케이션에서 사용자-아이템 그래프 또는 사용자-사용자 그래프에서 이웃을 발견하는 데 사용될 수 있다.
• 주어진 사용자로부터 랜덤-워크를 수행함으로써 이웃에 있는 다른 사용자를 발견할 수 있으며, 이는 개인화된 페이지 랭크 접근 방식을 직접 적용한 것이다.
• 사용자의 이웃이 발견된 후 이웃의 특정 랭킹을 사용해 예측할 수 있다.
• 사용자-아이템 그래프와 사용자-사용자 그래프 또는 아이템-아이템 그래프 모두로 작업할 수 있다.
• 아이템-아이템 그래프는 아이템들 간의 상관관계를 정의하기 때문에 상관 그래프라고도 한다.
• 이 경우 가중되고 방향이 있는 네트워크 G = (N , A)가 생성되는데, 여기서 N의 각 노드는 아이템에 대응하고, A의 각 에지는 아이템 간의 관계에 대응한다.
  • 아이템 i와 j가 최소한 한 명의 사용자에 의해 평가됐다면 방향 에지 (i , j)와
    (j , i)는 모두 네트워크에 존재한다.
  • 방향 네트워크는 에지 (i , j)의 가중치가 에지 (j ,i)의 가중치와 반드시 동일하지 않기 때문에 비대칭이다.
• 에지 (i , j)의 가중치는 다음과 같이 설정된다.

1. 에지 (i , j)의 가중치를 |Ui ◠Uj|로 설정한다.
2. 에지의 가중치가 정규화돼 노드의 나가는 에지 가중치의 합이 1이 된다.
3. 에지의 가중치가 랜덤 워크 확률에 해당하는 그래프를 만든다.

• 평점 행렬에 대한 상관관계 그래프의 예는 그리 10.4에 나와 있다.
  
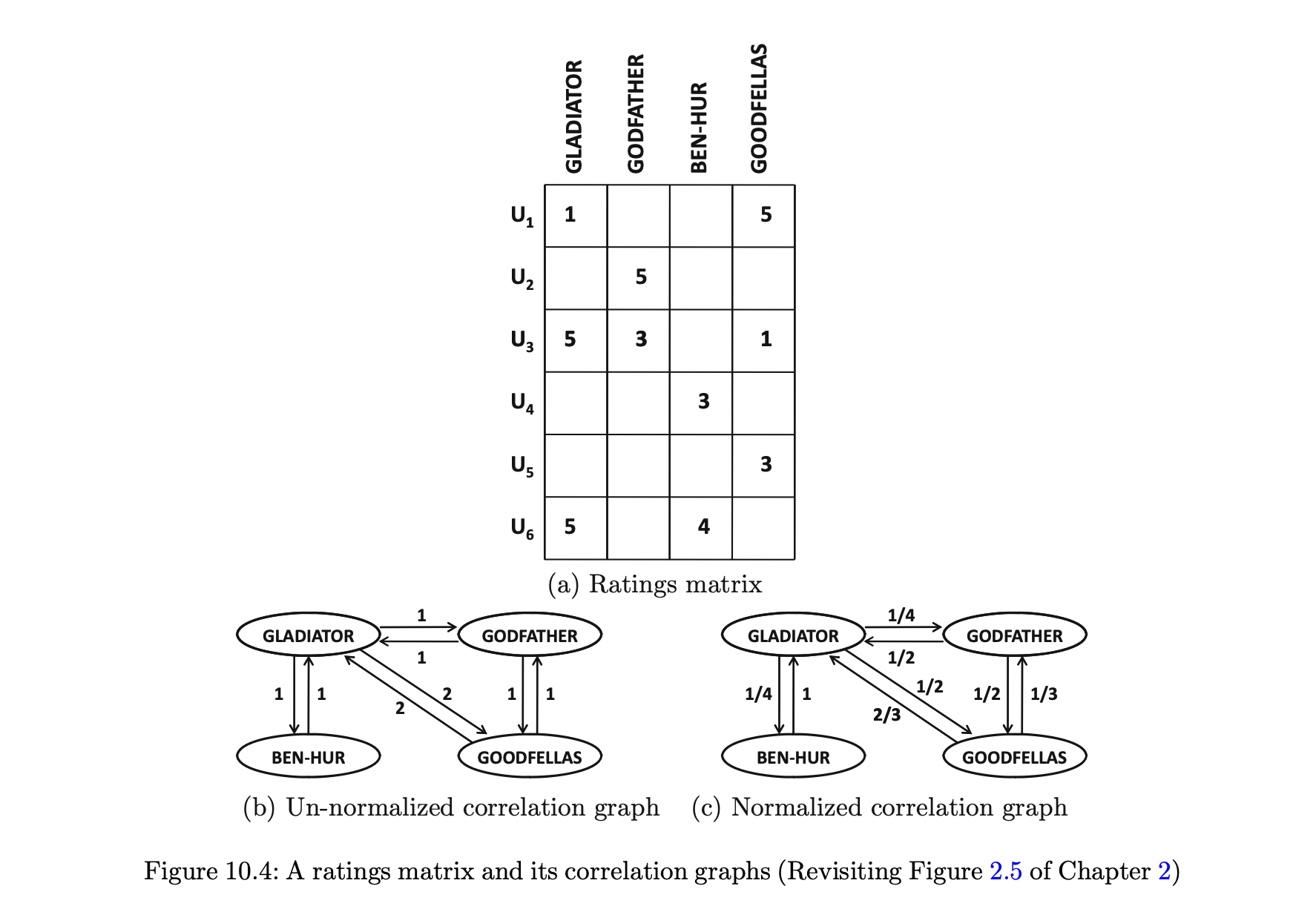
• 추천을 수행하기 위해서 다양한 개인화된 페이지 랭크 방법을 사용할 수 있으며 다음 두 가지 방법이 가장 일반적이다.

1. 관련 이웃 항목을 결정하기 위해 특정 아이템 노드에서 다시 시작해 랜덤 워크를 수행할 수 있으며, 기존의 아이템 기반 이웃 알고리듬을 사용해 해당 아이템의 평점을 예측할 수 있다.
2. 아이템 랭크라고 하는 접근 방식을 사용해 추천을 직접 수행할 수도 있으며, 이 경우 페이지 랭크 바이어스 벡터는 사용자가 다양한 아이템에 부여한 랭킹에 의해 영향을 받는다.

📖 유사도 랭크

• 일부 애플리케이션에서는 노드 간의 대칭 쌍별 유사도가 필요하다.
• 유사도 랭크 방법은 특정 쿼리 노드의 평찬이 좋은 이웃을 결정하는 데 사용할 수 있다.
• 유사도 랭크는 노드 간의 대칭적인 유사도를 결정한다.
  • 즉, 노드 i와 j 사이의 유사도는 j와 i 사이의 유사도와 동일하다.
  • 이러한 유사도 측정은 방향이 지정되지 않은 네트워크에만 적용된다.
• 유사도 랭크 방정식은 다음과 같이 재귀적으로 정의된다.
  
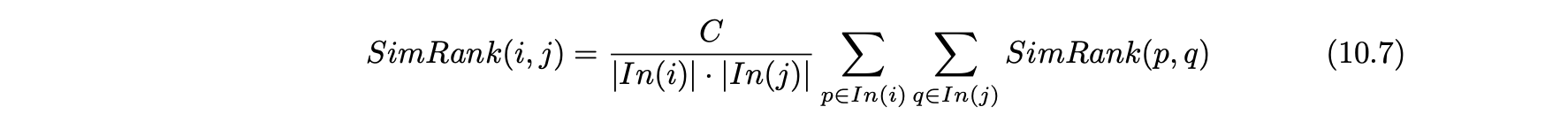
  • In(i)는 i의 인-링크 노드를 나타낸다.
  • C는 (0,1)의 재귀의 일종의 붕괴율로 볼 수 있는 상수다.
  • 알고리듬은 이후 모든 노드 쌍 사이의 유사도 랭크 값을 업데이트해 수렴에 도달할 때 까지 방정식 10.7을 반복적으로 상용한다.
  • C < 1이기 때문에 거리가 작을수록 유사도가 높아지고 거리가 멀수록 유사도가 낮아진다.
• 유사도 랭크 방법의 한 가지 단점은 각 사용자에게 공통 노드로의 경로 길이가 동일해야 한다는 거싱다.
• 결과적으로 동일한 길이의 경로가 공통 노드에 존재하지 않는 경우 직접 연결된 두 노드 사이의 유사도 랭크 값이 0이 될 수 있다.
• 예를 들어 그림 10.5에서 노드 A와 B는 길이 3의 경로만으로 연결되기 때문에 유사도 랭크는 노드가 제대로 연결돼 있더라고 항상 0이다.
• 반면에 노드 A와 C가 제대로 연결돼 있지 않더라도 노드 A와 C 사이의 유사도 랭크는 0이 아니다.
  
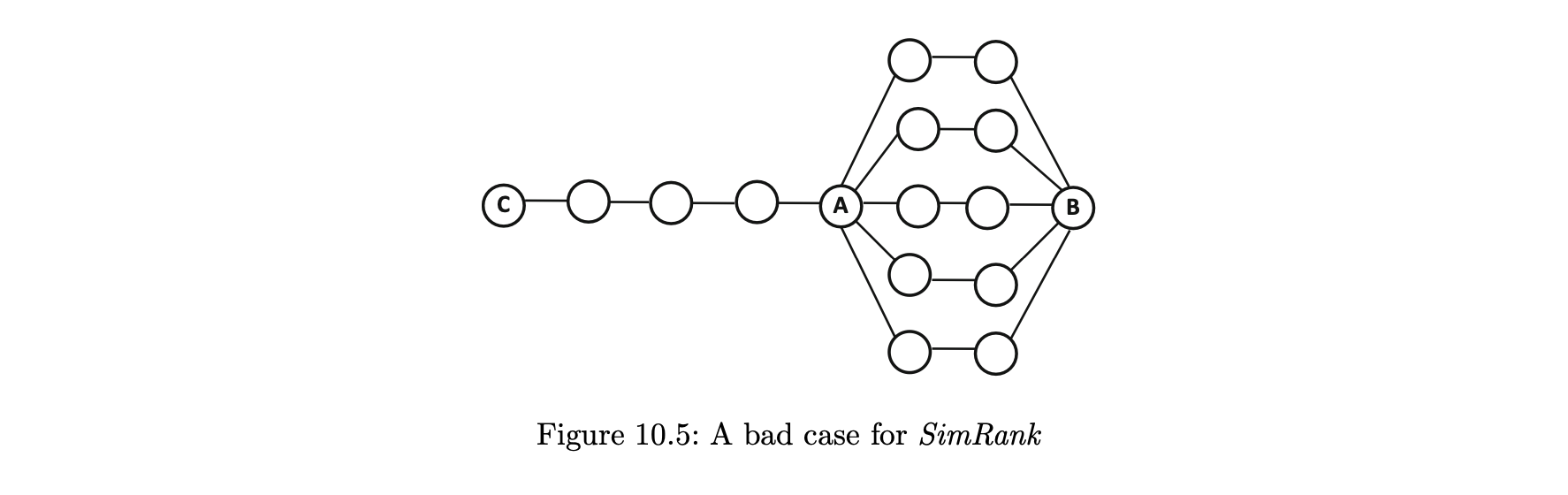
  • 유사도 랭크 접근법이 적용되지 않는 경우를 인식하는 것이 중요하다.
  • 예를 들어 이진 사용자 아이템 그래프에서 사용자 노드와 아이템 노드 사이의 모든 경로 길이가 홀수이기 때문에 사용자와 항목 노드 사이의 유사도 랭크 값은 항상 0이다.
  • 유사도 랭크 방법을 사용하면 사용자 쌍 간 또는 아이템 쌍 간 유사도를 효과적으로 계산할 수 있기 때문에 이러한 접근법은 사용자 피어 또는 아이템 피어를 개산함으로써 전통적인 협업 필터링 애플리케이션에서 이웃 기반 방법으로 사용될 수 있다.

📌 집단 분류에 의한 추천

• 집단적 분류 방법은 특히 추천 과정에 콘텐츠를 통합하는 데 효과적이다.
• 협업 필터링 문제와 마찬가지로 이는 네트워크 구조와 관련해 수행된다는 점을 제외하고는 불완전한 데이터 추정 문제다.
• 이 문제에 대한 해결책은 주어진 노드에 근접해 k 레이블이 부탁된 노드를 검사하고 대다수 레이블을 보고하는 것이지만, 이러한 접근 방식이 일반적으로 노드 레이블의 희소성 때문에 집단적 분류에서는 불가능하다.
• 그림 10.6의 테스트 노드의 경우, 일반적으로 네트워크 구조에서 A의 인스턴스에 더 가깝지만 테스트 인스턴스에 직접 연결된 레이블 노드는 없기 때문에 레이블 희소성의 문제는 평가 기반 데이터의 경우에서와 같이 네트워크 기반 예측과 관련해 발생한다.
  
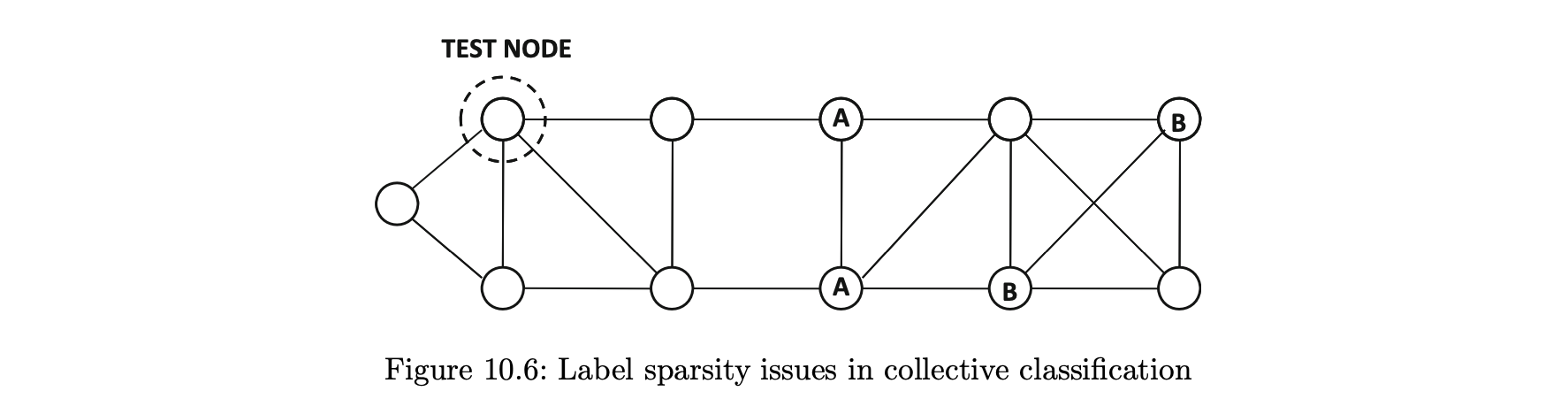
• 이러한 희소성 문제를 해결하기 위한 두 가지 알고리듬이 있다.

1. 반복 분류 알고리듬
2. 랜덤 워크 기반 방법

📖 반복 분류 알고리듬

• 반복 분류 알고리듬의 중요한 단계는 콘텐츠에서 이용 가능한 콘텐츠 기능 외에도 일련의 링크 특징을 도출하는 것이다.
• 가장 중요한 특징은 노드 바로 이웃에 있는 클래스의 분포에 해당한다.
  • 원칙적으로 노드의 정도, 페이지 랭크 값, 노드와 관련된 닫힌 삼각형의 수 또는 연결 기능과 같은 그래프의 구조적 특성에 근거한 다른 링크 기능을 도출하는 것도 가능하다.
  • 이러한 링크 특성은 네트워크 데이터 집합에 대한 애플리케이션별 이해를 기반으로 도출될 수 있다.
• 기본 반복 분류 알고리듬은 메타 알고리듬으로 구성된다.
  • 나이브 베이즈 분류 모델, 로지스틱 회귀 분류 모델 및 이웃 기반 분류 모델 등의 다양한 구현에 여러 가지 기본 분류 모델이 사용된다.
  • 주요 요건은 이러한 분류 모델이 특정 클래스에 속하는 노드의 가능성을 정량화하는 숫자 점수를 출력할 수 있어야 한다는 것이다.
• 링크 및 콘텐츠 기능은 이러한 분류 모델을 훈련시키는 데 사용된다.
  • 많은 노드들의 경우 레이블 희소성의 문제로 인해 이웃에 있는 다른 클래스가 존재하는 것과 같은 중요한 클래스별 특징들을 강력하게 추정하는 것이 어려우며, 노드의 클래스 예측을 신뢰할 수 없게 만든다.
  • 훈련 데이터 세트를 보강하기 위해 반복적인 접근 방식이 사용된다.
• 각 반복에서 nt/T 노드 레이블은 접근 방식에 의해 확실하게 만들어지고, 여기서 T는 최대 반복 횟수를 제어하는 사용자 정의 매개변수다.
  • 분류 모델이 가장 높은 평점의 클래스 확률을 나타내는 테스트 노드를 최종적으로 선택하면 레이블이 지정된 테스트 노드를 학습 데이터에 추가해 강화된 학습 데이터 세트로 링크 기능을 다시 추출해 분류 모델을 재교육한다.
  • 모든 노드의 레이블이 완성될 때 까지 이 접근 방식이 반복된다.
• 반복 분류 알고리듬의 장점은 분류 프로세스에서 콘텐츠와 구조를 완벽하게 사용할 수 있다는 것이다.
• 반면에 반복 분류의 초기 단계의 오류는 잘못된 레이블을 부착한 증강 훈련 예제로 인해 이후 단계에서 전파되고 증식될 수 있다는 한계점이 있다.

📖 랜덤 워크를 통한 레이블 전파

• 레이블 전파 방법은 방향이 지정되지 않은 네트워크 구조 G = (N , A)에서 랜덤 워크를 사용한다.
• 레이블이 없는 노드 i를 분류하기 위해 랜덤 워크가 노드 i 에서 시작해 첫 번째 레이블이 부착된 노드에서 종료된다.
  • 랜덤 워크가 종료 확률이 가장 높은 클래스는 노드 i의 예측 레이블로 보고된다.
  • 이 접근법의 직감은 노드 i에 근접한 레이블이 부착된 노드에서 랜덤 워크가 종료될 가능성이 높다는 것이다.
  • 따라서 특정 클래스의 많은 노드가 이웃해 있을 때 노드 i는 해당 클래스로 레이블이 지정될 가능성이 더 높다.
  • 중요한 가정은 그래프에 레이블이 연결돼 있어야 한다는 것이다.
• 첫 번째 단계는 레이블이 지정된 노드에 처음 도착할 때 항상 종료되는 방식으로 랜덤 워크를 모델링하는 것이다.
  • 이는 레이블이 있는 노드에서 송신 에지를 제거하고 이를 자체 루프로 교체하면 달성할 수 있다.
• 또한 랜덤-워크 방식을 사용하기 위해 무방향 그래프 G = (N, A)를 n x n 전이 행렬을 사용해 방향 그래프로 변환해야 한다.
  • 에지 전이 확률 pij는 다음과 같이 정의된다.
    
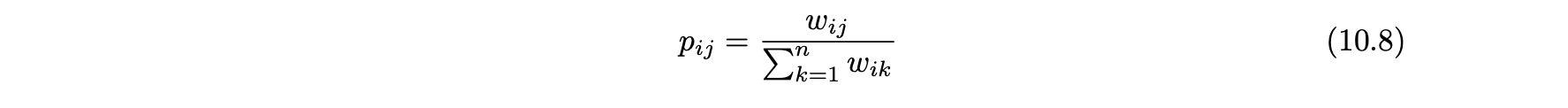
  • 에지 (j , i)의 전이 확률 pij는 다음과 같이 정의된다.
    
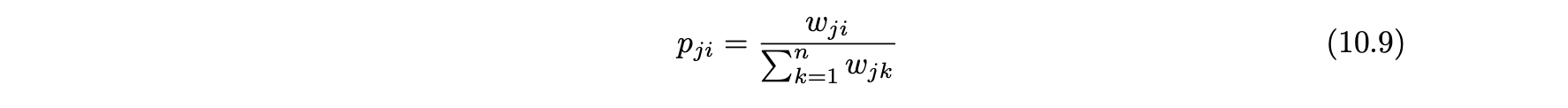
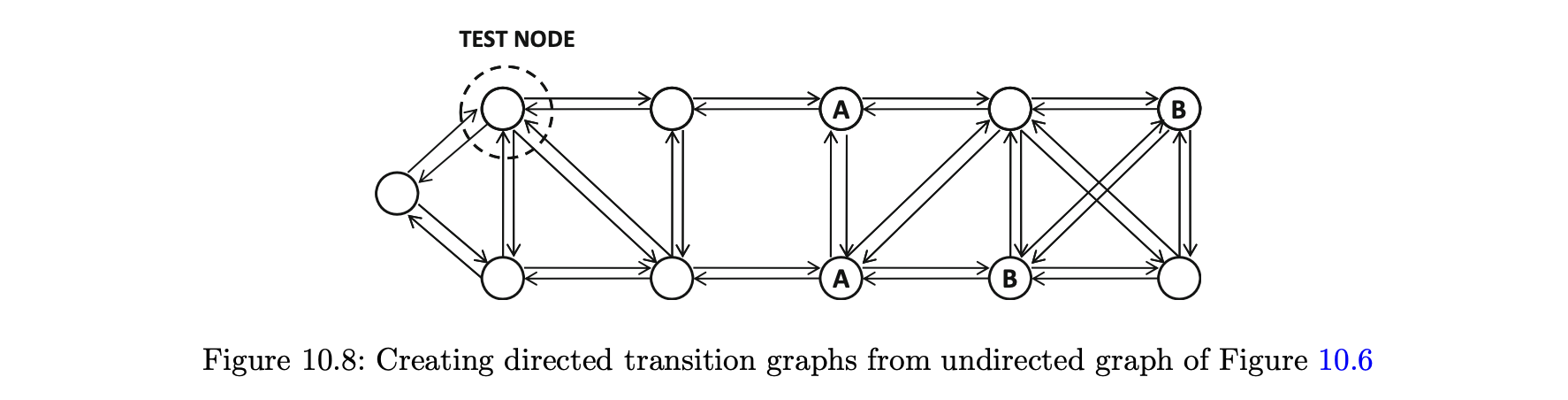
• 예를 들어 그림 10.6의 무방향 그래프에서 생성된 방향 전이 그래프는 그림 10.8에 나와 있다.
  

📖 소셜 네트워크에서 협업 필터링에 대한 적용성

• 집단적 분류 기법은 소셜 네트워크에서 사용자 협업 필터링에서도 사용될 수 있다.
• 다른 사용자가 지정한 다양한 제품에 대한 평점이 있는 시나리오를 고려하자.
  • 나아가 다양한 사용자의 소셜 연결에 해당하는 데이터도 보유하고 있다.
  • 따라서 이 문제는 전통적인 협업 필터링 문제의 일반화하고 볼 수 있다.
• 이 문제의 특정 버전은 집단 분류 방향을 사용해 쉽게 처리할 수 있다.
• 사용자가 아이템에 대한 좋아요를 지정할 수 있는 메커니즘은 있지만,
  싫어요를 지정할 수 있는 메커니즘은 없는 평점인 단항 평점을 생각해보자.
  • 이러한 경우 제품에 대한 선호도를 해당 노드에서 키워드로 포함시킬 수 있다.
  • 노드의 레이블은 관심 있는 특정 제품에 의해 정의되며, 다른 제품의 레이블은 콘텐츠 중심 키워드로 취급된다.
  • 이 문제는 노드상에서 콘텐츠를 사용하는 집단 분류 문제로 줄어들며, ICA 알고리듬으로 쉽게 처리할 수 있다.
  • 평점이 일률적이지 않은 경우, 각 제품의 평점은 별도의 레이블 집합 분류 문제를 모델링할 수 있다.
• 목표는 네트워크 구조와 함께 노드에서 지정된 평점을 사용해 다양한 아이템의 평점 값을 예측하는 것이다.

📌 친구 추천 : 링크 예측

• 많은 소셜 네트워크에서 네트워크의 노드 쌍 사이의 향후 링크를 예측하는 것이 바람직하다.
• 링크 예측에 일반적으로 사용되는 다양한 기법들이 존재한다.

📖 이웃 기반 척도

• 이웃 기반 척도는 향후 노드 간의 연결 가능성을 정량화하기 위해 서로 다른 방법으로 한 쌍의 노드 i와 j 사이의 공통 이웃 수를 사용한다.
• 예를 들어 그림 10.9(a)에서 앨리스와 밥은 4개의 공통 이웃을 공유하기 때문에 결국 그들 사이에 링크가 형성될 수 있다고 추측하는 것은 합리적이다.
  
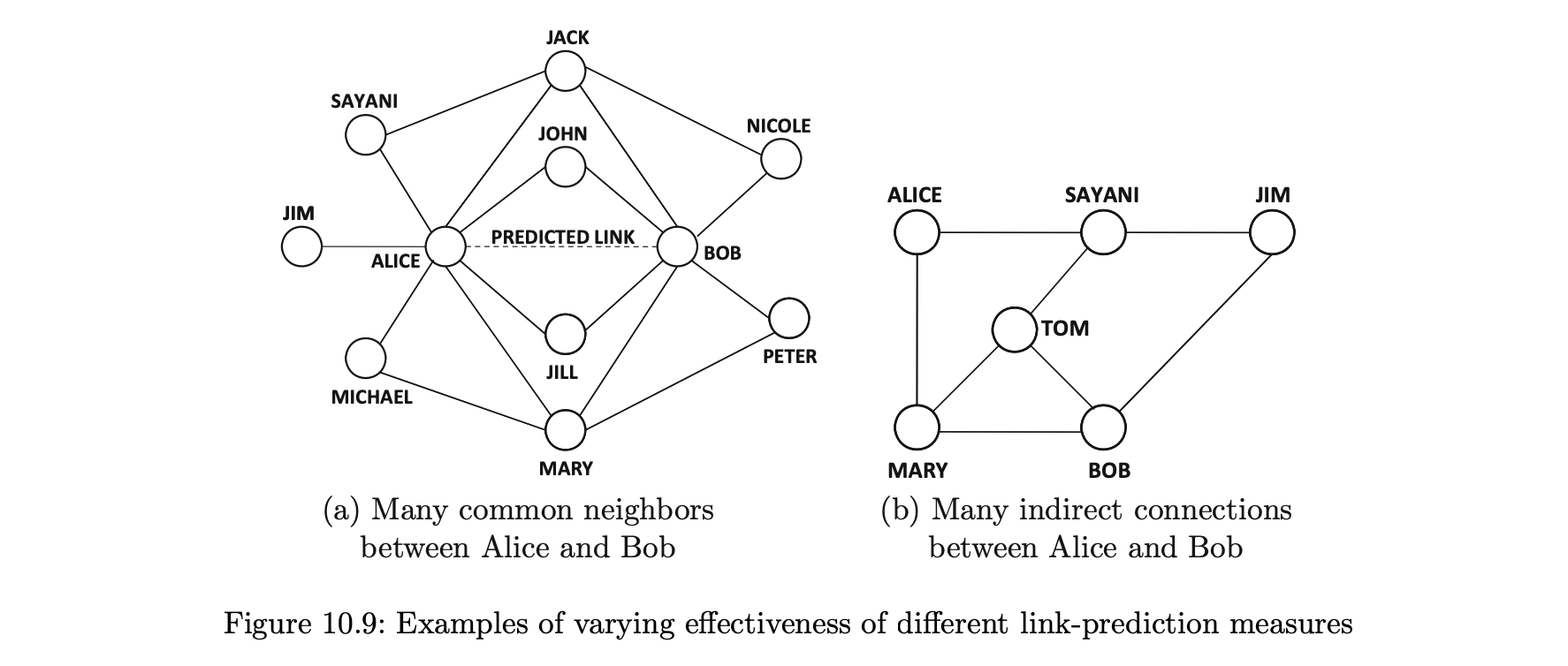
  • 그들은 공통의 이웃 외에도 그들만의 이웃을 갖고 있다.
  • 이웃의 수와 상대적인 중요성을 설명하기 위해 이웃 기반 조치를 정상화하는 방법은 다양하게 있다.
• 공통 이웃 측정 값은 다음과 같이 정의된다.
  
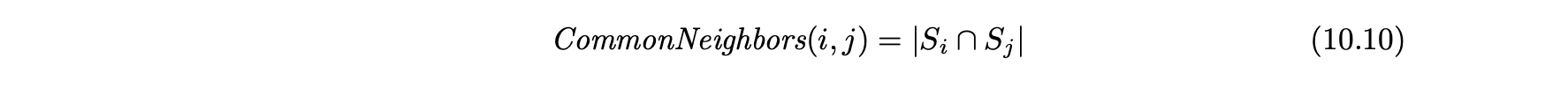
  • 공통 이웃 측정의 주요 약점은 다른 연결된 수와 비교할 때 그들 사이의 이웃의 상대적인 수를 고려하지 않는다는 것이다.
• 노드 i와 j 사이의 Jaccard 기반 링크 예측 측정 값은 각각 이웃 집합 사이의 Jaccard 계수와 같다.
  
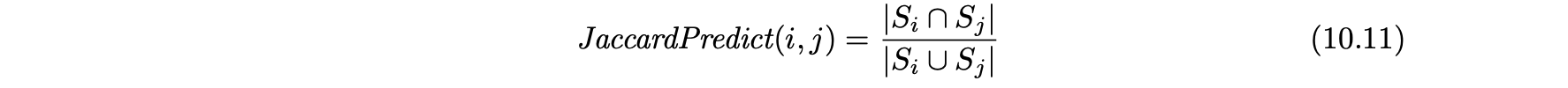
  • 그림 10.9(a)에서 앨리스와 밥 사이의 Jaccard 측정 값은 4/9이다.
  • 앨리스나 밥의 도수가 증가한다면, 그들 사이의 Jaccard 계수는 더 낮아질 것이다.
  • Jaccard 측정은 링크 예측이 측정되는 노드의 정도에 따라 훨씬 더 잘 조정되지만, 중간 이웃의 정도에 잘 맞지 않는다.
  • 예를 들어 그림 10.9(a)에서 앨리스와 밥의 공통 이웃은 잭, 존, 질 및 메리이지만, 이러한 공통의 이웃은 모두 매우 인기 있는 공인일 수 있기 때문에 이러한 노드는 통계적으로 여러 쌍의 노드의 공통 이웃으로 발생할 가능성이 높다.
• Adamic-Adar 측정법은 서로 다른 공통 이웃의 중요성을 설명하기 위해 고안됐다.
  • 공통 이웃의 가중치는 노드 도수의 감소함수의 공통 이웃 측정 값의 가중치 버전으로 볼 수 있다.
  • Adamic-Adar 측정의 경우에 사용되는 일반적인 기능은 역 로그이다.
  • 노드 i와 j 사이의 공통 이웃 측정 값의 노드 i와 j 사이의 가중 공통 이웃 수와 같다.
    
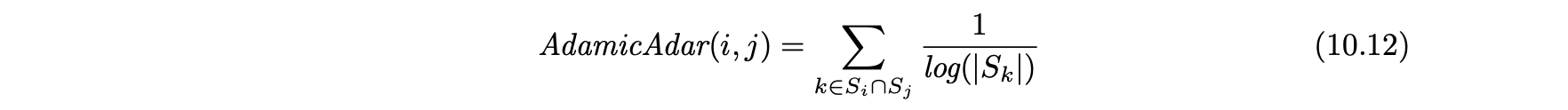
  • 그림 10.9(a)에서 앨리스와 밥 사이의 Adamic_Adar 측정 값은 다음과 같다.
    

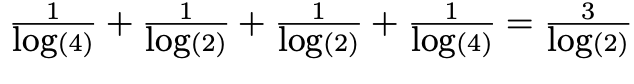
📖 카츠 척도

• 이웃 기반 척도는 한 쌍의 노드 사이에 링크가 형성될 가능성에 대한 강력한 추정치를 제공하지만 한 쌍의 노드 사이의 공유된 이웃의 수가 적을 때는 그다지 효과적이지 않다.
  • 그림 10.9(b)의 경우 앨리스와 밥은 하나의 이웃을 공유하며, 앨리스와 짐도 하나의 이웃만을 공유한다.
  • 이러한 경우에 이웃 기반 척도는 상이한 쌍의 예측 강도를 구별하는 데 어려움이 있다.
• 이러한 경우에는 워크 기반 측정이 더 적합하다.
• 링크 예측 강도를 측정하기 위해 일반적으로 사용되는 특정 워크 기반 측정 값은 카츠 척도이다.
• 카츠 척도는 다음과 같이 정의된다.
  
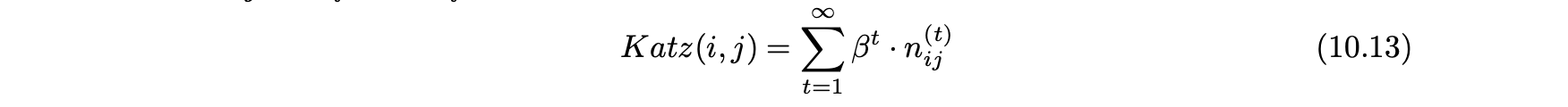
  • β 값은 더 긴기 길이의 보행을 강조하지 않는 할인 요소이다.
  • 충분히 작은 β 값에 대해 식 10.13의 무한 합은 수렴된다.
• A가 무방향 네트워크의 대칭 이웃 행렬인 경우, n x n 쌍의 카츠 계수 행렬 K는 다음과 같이 계산할 수 있다.
  

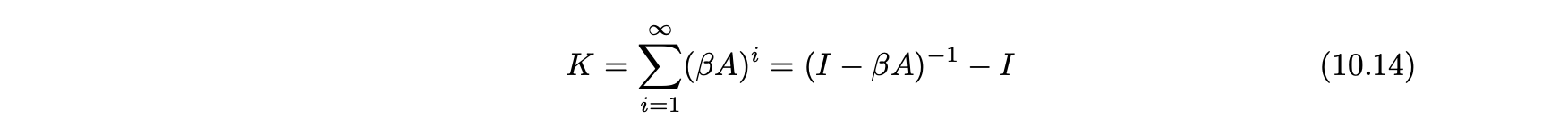
📖 랜덤 워크 기반 척도

• 랜덤 워크 기반 척도는 노드 쌍 간의 연결을 정의하는 다른 방법이 있다.
• 이러한 두 가지 방은은 페이지 랭크와 유사도 랭크이다.
• 노드 i와 j 사이의 유사도를 계산하는 첫 번째 방법은 노드 i에서 재시작은 수행되는 노드 j에서 개인화된 페이지 랭크를 사용하는 것이다.
  • j가 i의 구조적 접근성이면, 노드 i에서 재시작이 수행될 때 매우 높은 개인화된 페이지 랭크 측정 값을 갖게 된다는 것이다.
  • 이는 노드 i와 j사이의 높은 링크 예측 강도를 나타낸다.

📖 분류 문제로서의 링크 예측

• 링크 예측 문제는 한 쌍의 노드 사이에 링크의 유무를 이진 클래스 지표로 처리함으로써 분류 문제로 볼 수 있다.
• 따라서 각 쌍의 노드에 대해 다차원 데이터 레코드를 추출할 수 있다.
  • 이 다차원 레코드의 특징은 노드 간의 모든 다른 이웃 기반, 카츠 기반 또는 워크 기반 유사도를 포함한다.
• 또한 쌍에 있는 각 노드의 노드 도수와 같은 여러 가지 다른 우선 첨부 기능이 사용된다.
• 각 노드 쌍에 대해 다차원 데이터 레코드가 구성된다.
  • 레이블이 없는 양의 분류 문제로 에지가 있는 노드 쌍은 양의 예이고 나머지 쌍은 레이블이 없는 예이다.
  • 크고 희박한 네트워크에는 부정적인 예제 쌍이 너무 많기 때문에 부정적인 예제의 샘플만 사용된다.
  • 따라서 지도 링크 예측 알고리듬은 다음과 같이 작동한다.
  1. 훈련 단계
     • 에지가 있는 각 노드 쌍에 대해 하나의 데이터 레코드를 포함하고, 에지가 없는 노드 쌍의 데이터 레코드 샘플을 포함하는 다차원 데이터 세트를 생성한다.
     • 특징들은 추출된 유사도 및 노드 쌍들 사이의 구조적 특징에 해당한다.
     • 클래스 레이블은 쌍 사이에 엣지가 있는지를 의미한다.
     • 데이터에 대한 훈련 모델을 구성한다.
  2. 테스트 단계
     • 각 테스트 노드 쌍을 다차원 레코드로 변환한다.
     • 기존의 다차원 분류 모델을 사용해 레이블을 예측한다.
  • 이 접근 방식의 장점은 콘텐츠 기능을 원활하게 사용할 수 있다는 것이다.
  • 이 접근법은 비대칭 방식으로 특징을 추출함으로써 방향 네트워크를 처리할 수 있다.

📖 링크 예측을 위한 행렬 인수분해

• 협업 필터링과 마찬가지로 링크 예측 방법은 암시적 피드백 행렬의 행렬 완성 문제로 볼 수 있다.
• 방향 그래프의 경우, 인수 분해는 협업 필터링과 매우 유사하다.
  
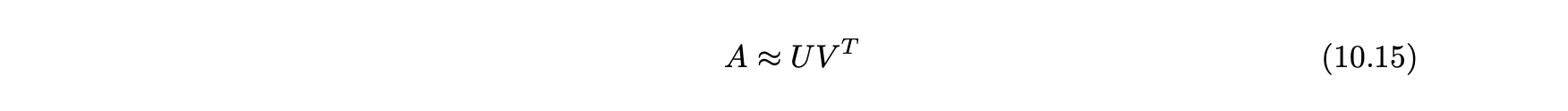
  • A는 그래프의 이웃 행렬이다.
  • U와 V를 학습 후에는 가장 큰 예측 가중치를 가진 에지를 추천할 수 있다.
  • 행렬 A는 암묵적 피드백 행렬과 유사한 방식으로 볼 수 있는데, 여기에는 양과 음의 샘플이 모두 필요하다.
  • 긍정적 및 부정적 항목을 다음과 같이 정의한다.
    
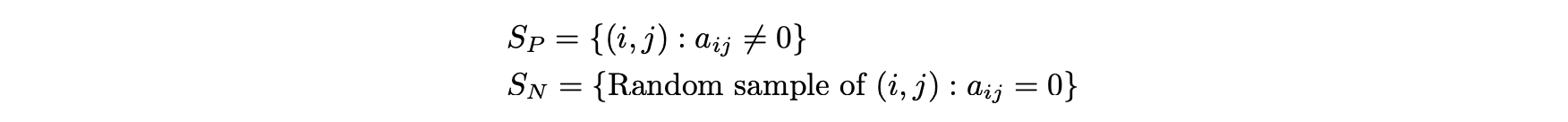
• 임의의 원소에 대해 다음과 같이 예측할 수 있다.
  
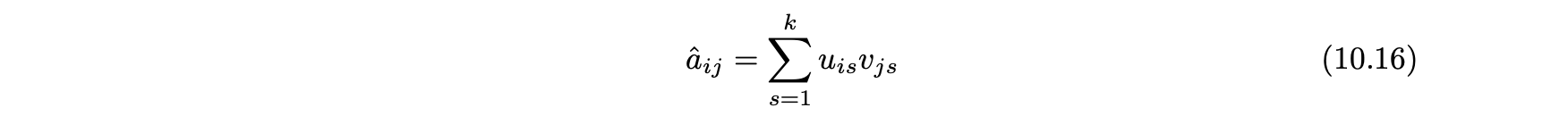
• 오류를 최소화하고자 하는 정규화된 목적함수는 다음과 같다.
  
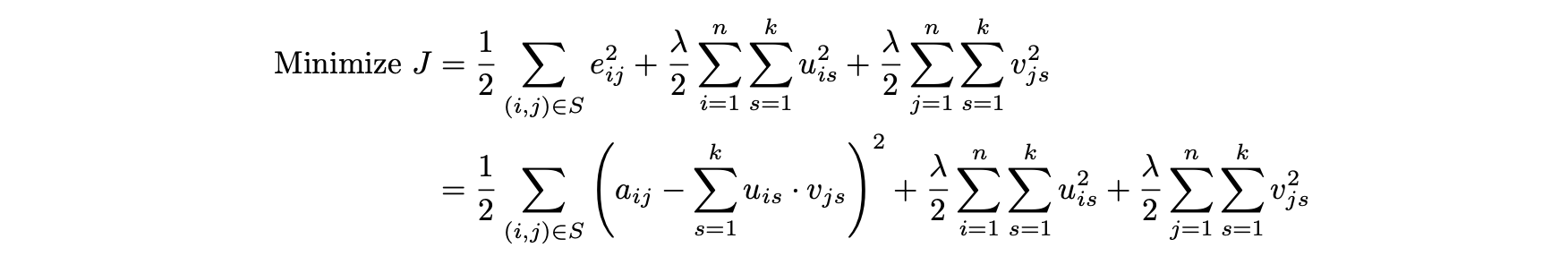
• 모든 엔트리들에 대한 에러에 따른 기울기가 계산되는 벡터화된 기울기 감소 또는 랜덤하게 선택된 에지들에 대한 에러들을 이용해 도함수가 확률적으로 근사치인 확률 그레이디언트 디센트를 사용할 수 있다.
  • 정규 그레이디언트 디센트에서 행렬 U와 V는 무작위로 초기화되며 U의 각 항목 (i , q)과 V의 각 항목 (j , q)에 대해 다음 업데이트가 반복적으로 실행된다.
    
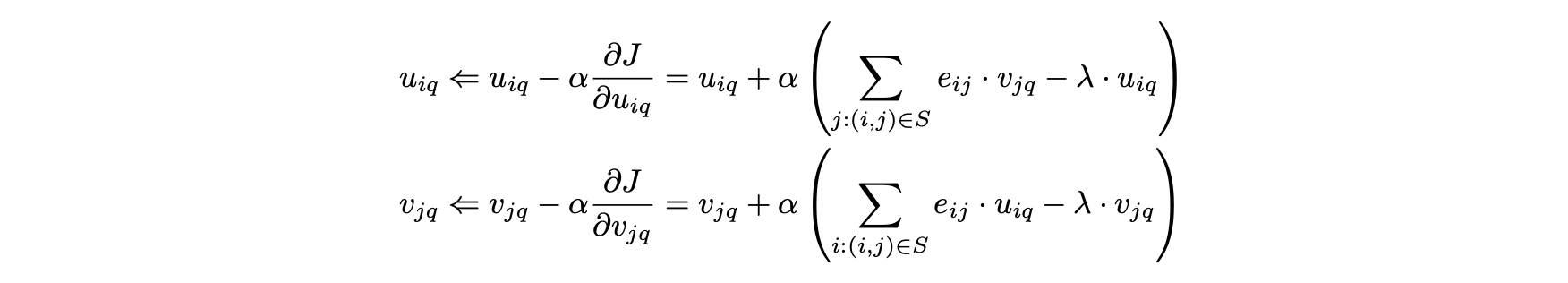
• 이후 업데이트는 다음과 같이 계산될 수 있다.
  
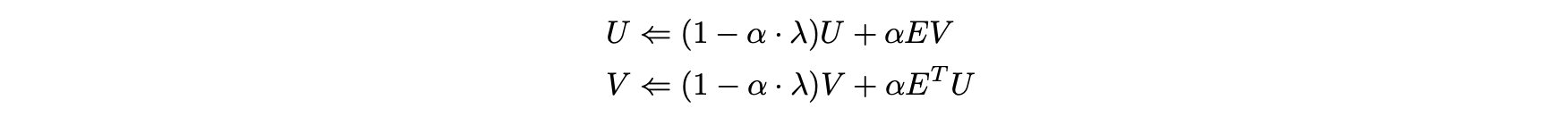
• 확률 경사하강의 기본 아이디어는 단일 항목으로 인한 오류 구성 요소와 관련해 기울기를 확률적으로 근사화하는 것이다.
  • 집합의 에지는 랜덤하게 순서대로 처리되고, 잠재 인자는 그 에지에 대한 에러 그레이디언트에 기초해 업데이트 된다.
  • U 및 V의 무작위 초기화로 시작해 무작위로 선택된 항목과 관련해 다음 업데이트를 사용할 수 있다.
    
• 앞에서 설명한 표현식을 확장하고 다른 값들에 대한 업데이트들을 해당 U 또는 V 행의 단일 벡터화된 업데이트로 통합할 수 있다.
  • 확률적 경사 하강 업데이트는 다음과 같이 작성될 수 있다.
    
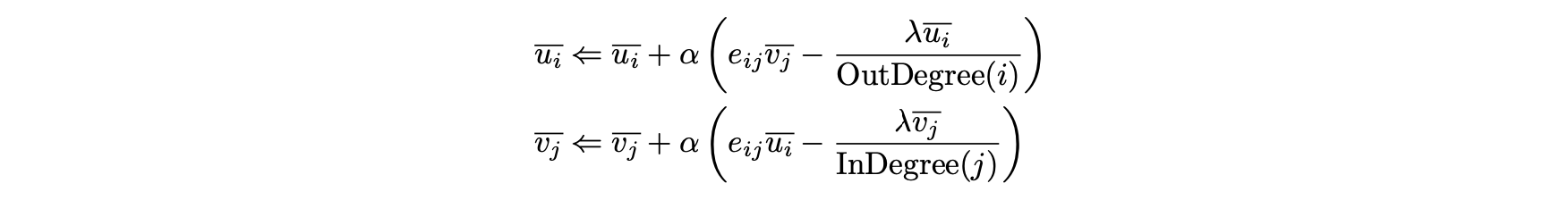
  • 수렴에 도달할 때 까지 S의 다양한 에지를 계속 순환한다.

1. 대칭 행렬 인수분해

• 무방향 그래프의 경우 행렬 A가 대칭이므로 별도의 인자 행렬 U 와 V가 필요하지 않다.
  • 최적화 파라미터를 더 적게 사용하면 과적합을 줄일 수 있다는 이점이 있다.
  • 이 경우 단일 인자 행렬 U를 사용해 다음과 같이 인수분해를 나타낼 수 있다.
    
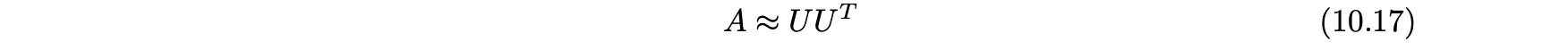
• 각 관측된 값은 다음과 같이 예측될 수 있다.
  
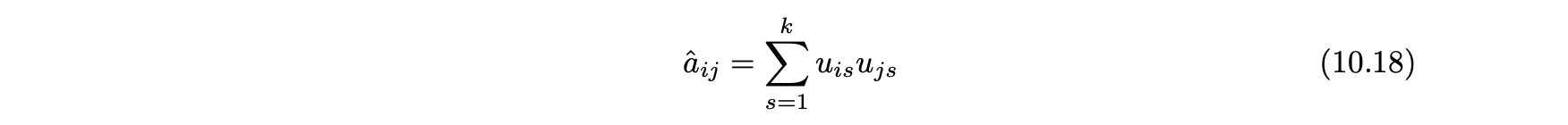
• 관찰된 항목에서 오류를 최소화하기 위해 정규화된 목적함수는 다음과 같다.
  
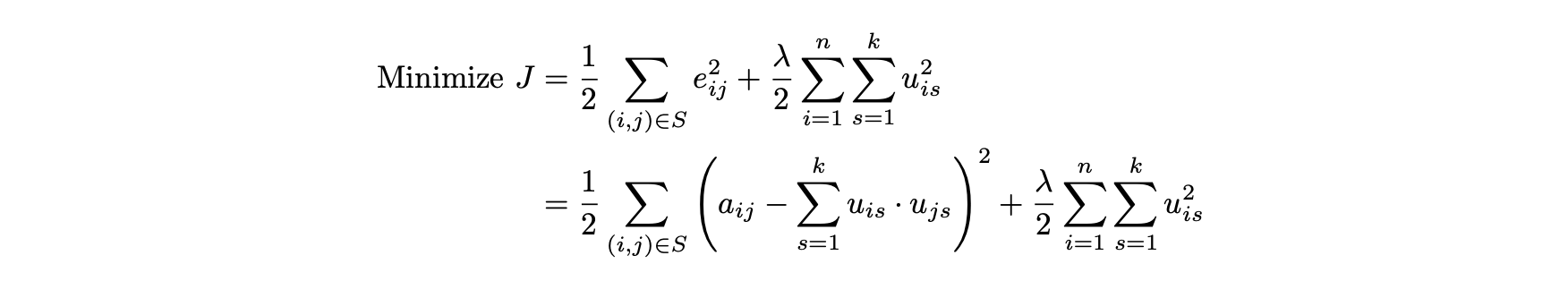
• 의사 결정 변수에 대해 J의 편도 함수를 취하면 다음과 같은 결과를 얻을 수 있다.
  
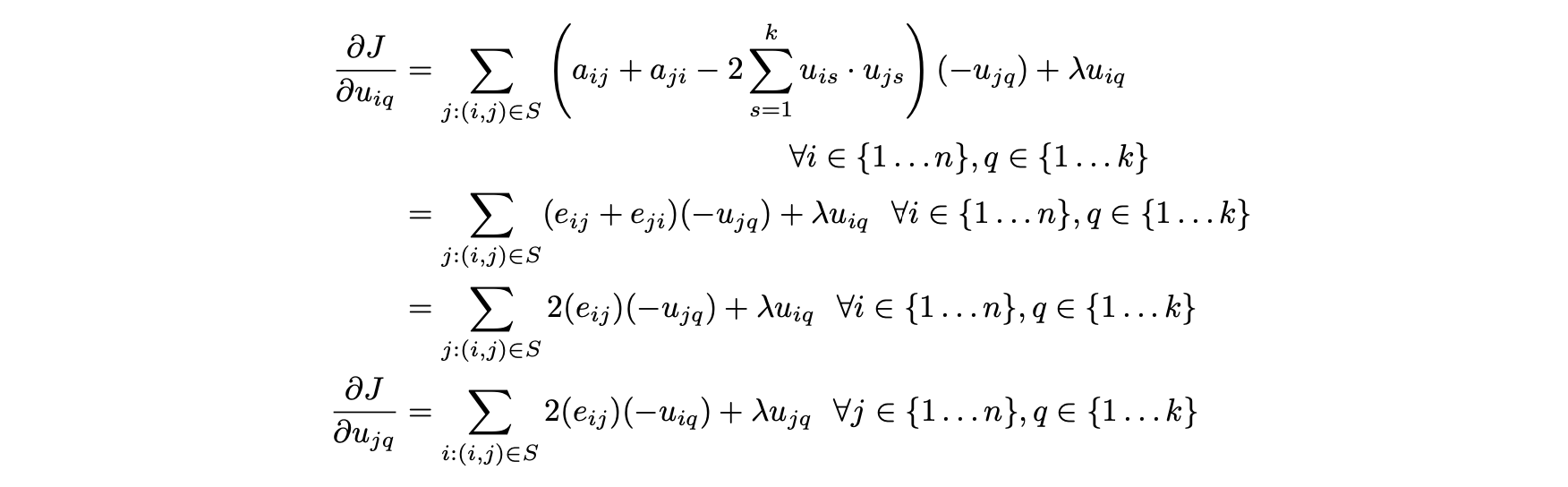
• 이후 다음과 같이 최소 행렬 곱셈을 사용해 업데이트를 수행할 수 있다.
  
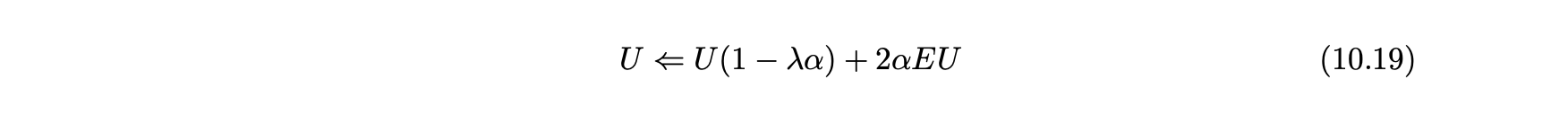
• 결과적인 솔루션의 품질은 일반적으로 낮지만 확률적 경사하강법은 더 빠른 수렴을 위해 사용될 수 있다.
  
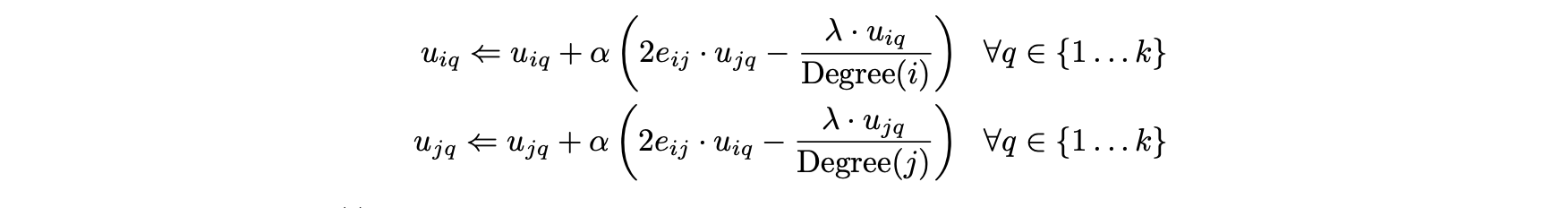
  • 여기서 Degree(i)는 SN의 '에지'를 포함해 i에 발생하는 에지 수를 나타낸다.
• U의 i번째 행 및 j 번째 행과 관련해 이러한 업데이트를 작성할 수도 있다.
  
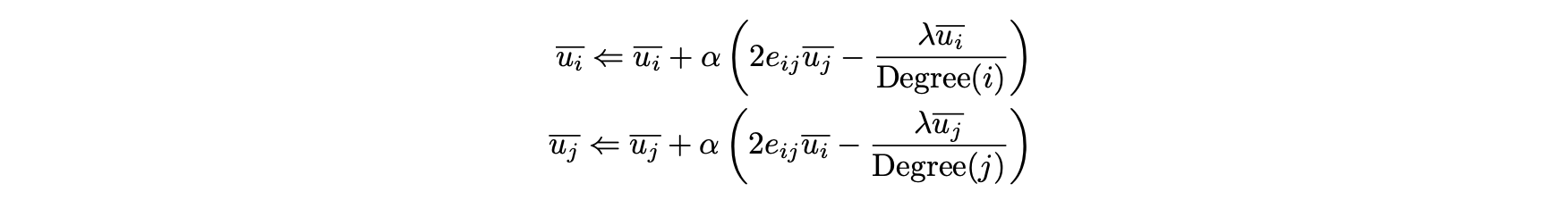
  • λ 값은 일반적으로 교차 검증 방법을 사용하거나 홀드 아웃 집합에서 다양한 λ 값을 시도해 선택된다.

📖 링크 예측과 협업 필터링 간의 연결

• 링크 예측과 협업 필터링은 결측값을 추정하려고 시도한다.
• 링크 예측은 링크의 존재가 단일 평점과 유사한 협업 필터링의 암묵적 피드백 설정과 매우 유사하다.
• 사용자-아이템 그래프의 개념은 링크 예측과 협업 필터링 간의 자연스러운 연결을 제공한다.
• 단일 평점의 경우 기존 링크 예측 방법을 사용자 항목 그래프에 적용할 수 있다.
• 사용자 노드와 항목 노드 사이의 링크의 예측 강도는 해당 사용자가 해당 항목을 얼마나 좋아하는지에 관한 예측이다.
• 이 연결로 인해 링크 예측 방법을 사용해 협업 필터링을 수행할 수 있다.

1. 협업 필터링에 링크 예측 알고리듬 사용

• 사용자-아이템 그래프에서 사용자 노드에서 형성될 가능성이 있는 상위 -k 사용자-아이템 링크를 예측함으로써, 사용자에 대한 상위-k 항목을 예측할 수 있다.
• 이 접근 방식은 사용자의 소셜 네트워크 구조가 알려진 경우에도 사용할 수 있는 것이 주목할 만하다.
  • 이 경우 사용자들 사이에 에지는 링크 예측 프로세스 내에 포함된다.
  • 그러한 에지를 포함하면 추천 프로세스 내에 소셜 링크의 동질성 효과를 통합하는 결과를 가져올 것이다.
• 사용자가 항목을 좋아하거나 싫어하는 것에 해당하는 평점이 {-1 , +1}에서 도출되는 경우를 생각해보자.
  • 이 경우 에지에는 평점에 대한 부호가 표시된다.
  • 평점이 이진인 경우의 예는 각각 그림 10.11(c)와 10.11(d)에 설명돼 있다.
    
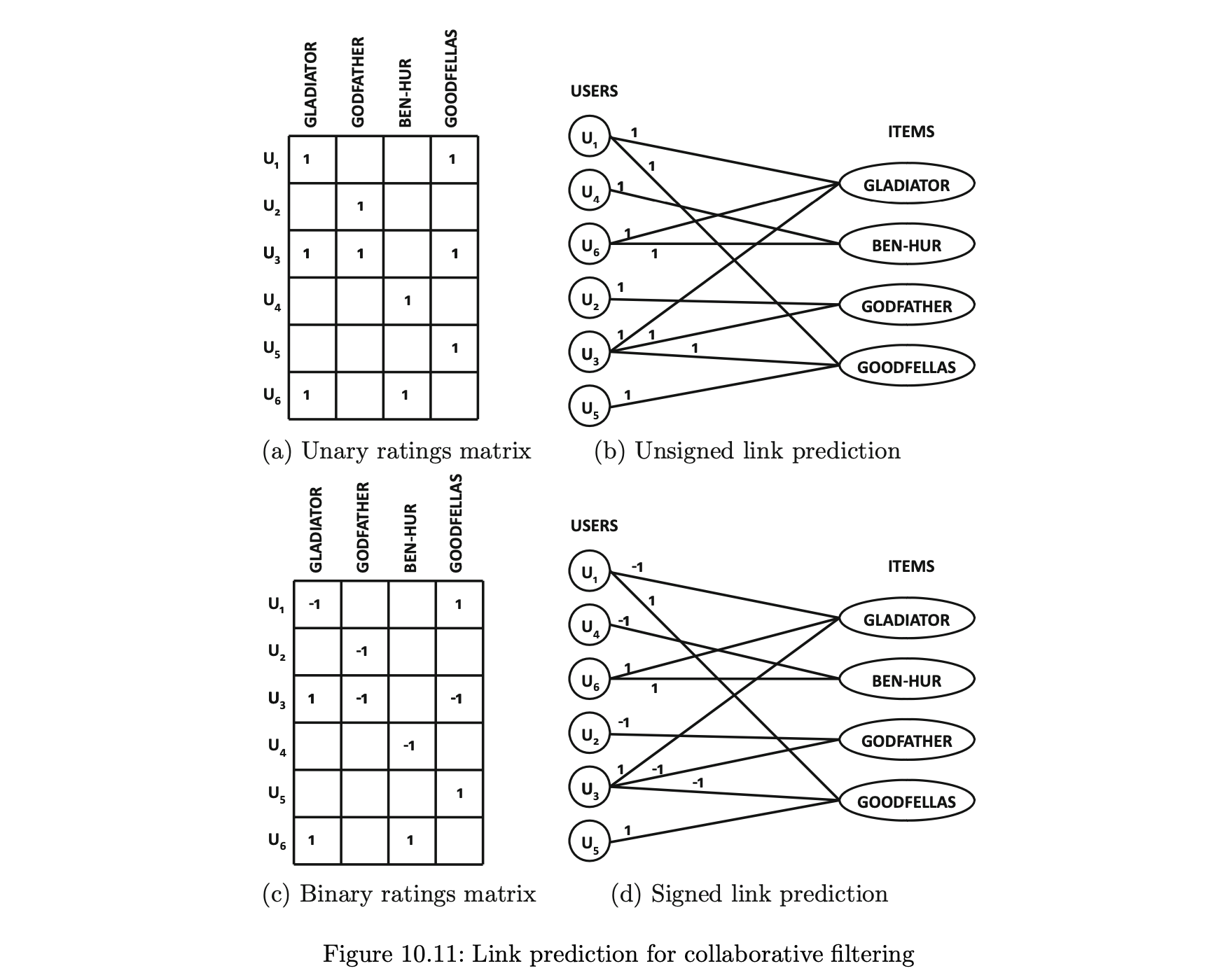
  • 이진 평점의 결과 네트워크는 부호 있는 에트워크이며, 사용자가 가장 좋아하는 항목을 결정하기 위해 사용자에게 발생하는 최상위-k 양의 링크를 예측하는 것이 바람직하다.
  • 최상위-k 개의 링크를 예측함으로써 사용자가 가장 싫어하는 최상위-k 항목을 발견할 수도 있다.
  • 이 문제는 부호 있는 네트워크에서 긍정적 또는 부정적 링크 예측의 문제이다.
• 링크 예측 방식은 임의의 평점을 사용할 수도 있지만 단항 또는 이항 평점 데이터에 효과적이다.

2. 협업 필터링 알고리듬을 사용한 링크 예측

• 협업 필터링과 링크 예측 모두 결측값 추정 문제다.
  • 유일한 차이점은 협업 필터링이 사용자 아이템 행렬에서 수행되는 반면,
    링크 예측은 노드-노드 행렬에서 수행된다는 것이다.
• 행렬 차수의 차이가 알고리듬의 성능에 영향을 줄 수 있지만, 상대적으로 인식되지 않는 사실은 사실상 모든 협업 필터링 방법이 링크 예측에 사용될 수 있다는 것이다.
  • 협업 필터링 알고리듬의 어느 정도의 적응이 필요하다.
  • 예를 들어 링크 예측을 위해 거의 모든 이웃 기반 방법, 희소 선형 모델 및 행렬 인수분해 방법을 사용할 수 있다.

📌 사회적 영향 분석 및 입소문 마케팅

• 모든 사회적 상호작용은 개인마다 다양한 수준의 영향을 미친다.
• 이 일반적인 원칙은 온라인 소셜 네트워크에도 적용된다.
• 시장 참여자에게 영향을 미치는 이 방법론을 입소문 마케팅이라 한다.
• 배우마다 소셜 네트워크에서 피어에게 영향을 줄 수 있는 능력이 다르다.
• 배우의 영향력을 조절하는 가장 일반적인 두 가지 요소는 다음과 같다.

1. 소셜 네트워크 구조 내에서 배우의 중심성은 그의 영향력 수준에 결정적인 요소다.
2. 네트워크의 에지는 종종 해당 행위자 쌍이 서로 영향을 받을 수 있는 가능성에 의존하는 가중치와 연관된다.

• 영향 전파 모델은 위에서 언급한 요인의 정확한 영향을 계량화하는 데 사용된다.
  • 영향 전파 모델의 주요 목표는 정보 보급에 따른 영향을 최대화하는 시드 노드 세트를 결정하는 것이다.
  • 영향 전파 모델은 가맹점에 대한 가치 있는 사회 행위자의 추천 모델로 볼 수 있다.
• 영향 최대화 문제는 다음과 같다.
  소셜 네트워크 G = (N , A)가 주어지면 k 개의 시드 노드 세트 S를 결정해 네트워크의 전체적인 영향 확산을 최대화 할 수 있다.
  • k의 값은 초기에 영향을 받을 수 있는 시드 노드 수에 대한 예산으로 볼 수 있다.
  • 이는 광고주가 초기 광고 능력에 대한 예산에 직면하는 실제 모델과 일치한다.
  • 사회적 영향 분석의 목표는 입소문 방법으로 이 초기 광고 능력을 확장하는 것이다.
• 각 모델 또는 휴리스틱은 f(•)로 표시되는 S의 함수를 사용해 노드의 영향 수준을 수량화 할 수 있다.
  • 이 함수는 노드의 하위 집합을 영향력 값을 나타내는 실수로 매핑한다.
  • 따라서 주어진 집합 S의 영향 f(S)를 정량화하기 위해 모델이 선택된 후, 최적화 문제는 f(S)를 최대화하는 집합 S를 결정하는 것이다.
  • 흥미로운 점은 최적화된 함수 f(S)가 하위 모듈이라는 것이다.
• 하위 모듈이란 집합에 적용되는 것처럼 수익 감소의 자연 법칙을 나타내는 수학적 법이다.
  • 집합 S의 하위 모듈은 공식적으로 다음과 같이 정의된다.
    
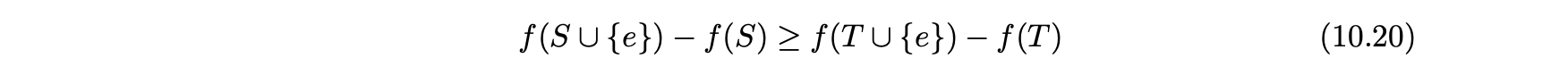
• 주어진 S값에 대해 f(S)를 평가할 수 있는 한 하위 모듈 함수를 최대화하기 위해 매우 효율적인 탐욕 최적화 알고리듬이 존재하기 때문에 하위 모듈 방식은 알고리듬적으로 편리하다.
  • 이 알고리듬은 S = { }를 설정해 시작하고 가능한 한 f(S)의 값을 증가시키는 노드를 S에 점차적으로 추가한다.
  • 이 절차는 집합 S에 필요한 개수의 영향 요인 k가 포함될 때 까지 반복된다.
• 노드 집합 S의 영향 함수 f(S)를 정의하기 위한 두 가지 일반적인 접근 방식은 선형 임계값 모델과 독립적 계단식 모델이다.
  • 이러한 확산 모델에서 일반적인 운영 가정은 노드가 활성 또는 비활성 상태라는 것이다.
  • 활성 노드는 원하는 동작 집합에 의해 이미 영향을 받은 노드이다.
  • 노드가 활성화 상태로 이동하면 노드는 결코 비활성화되지 않는다.
  • 모델에 따라 활성 노드는 한 번 또는 더 오랜 기간 동안 이웃 노드의 활성화를 트리거할 수 있다.
  • 노드는 주어진 반복에서 더 이상 노드가 활성화되 않을 때 까지 연속적으로 활성화된다.
  • f(S)의 값은 종료 시 활성화 된 총 노드 수로 평가된다.

📖 선형 임계값 모델

• 이 모델에서 알고리듬은 초기에 활성 시드 노드 집합 (S)으로 시작하고 이웃하는 활성 노드의 영향에 기초해 활성 노드의 수를 반복적으로 증가시킨다.
• 활성 노드는 더 이상의 노드를 활성화 할 수 없을 때까지 알고리듬을 실행하는 동안 여러 번 반복해 이웃 노드에 영향을 줄 수 있다.
• 이웃 노드의 영향은 에지 특정 가중치의 선형 함수를 사용해 정량화된다.
  • 네트워크 G=(N, A)의 각 노드 i에 대해 다음이 참이라 가정한다.
    
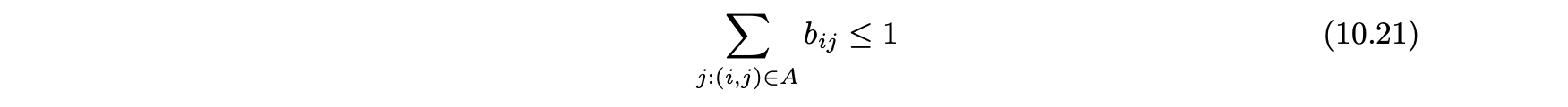
  • 각각의 노드 i는 미리 고정되고 알고리듬 과정에서 일정하게 유지되는 랜덤 임계값 θi~U[0 , 1]과 연관된다.
• 주어진 시간 내에서 노드 i의 활성 이웃의 총 영향 I(i)은 i의 모든 활성 이웃의 가중치의 합으로 계산된다.
  
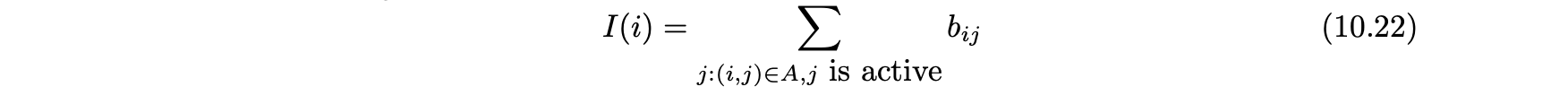
  • 노드 i는 I(i) >= θi 일때 활성화된다.
  • 이 프로세스는 더 이상 노드를 활성화할 수 없을 때까지 반복한다

📖 독립 캐스케이드 모델

• 독립형 캐스케이드 모델에서 노드가 활성화된 후 에지와 관련된 전파 확률로 이웃 노드를 활성화 할 수 있는 단일 기회만 얻는다.
• 각 반복에서 새로 활성화된 노드만 아직 활성화되지 않은 이웃 노드에 영향을 줄 수 있다.
• 주어진 노드 j에 대해 이를 새로 활성화된 이웃 노드 i에 결합하는 각 에지 (i , j)는 성공 확률과 독립적으로 동전 던지기를 한다.
  • 에지 (i , j)에 대한 동전 던지기가 성공하면 노드 j가 활성화된다.
  • 노드 j가 활성화되면 다음 반복에서 이웃 항목에 영향을 줄 단일 기회를 얻게 된다.
  • 반복에서 새로 활성화된 노드가 없는 경우 알고리듬이 종료된다.
• 영향 함수 값은 종료 시 활성 노드 수와 같다.
• 노드가 알고리듬을 진행하는 동안 최대 한 번만 영향을 줄 수 있기 때문에 알고리듬이 진행되는 동안 각 에지에 대해 코인이 던져진다.

📖 영향 함수 평가

• 선형 임계값 모델과 독립형 캐스케이드 모델은 모두 모델을 사용해 영향 함수 f(S)를 계산하도록 설계됐다.
  • f(S)의 추정은 일반적으로 시뮬레이션으로 수행된다.
• 영향 분석을 위한 가장 합리적인 모델은 하위 모듈성을 충족한다.

📖 소셜 스트림의 목표 영향 분석 모델

• 앞에서 언급한 영향 분석 모델은 매우 정적이며 특정 관심 주제에 대해 완전히 무관하다.
• 확률의 결정은 그러한 정보가 소셜 스트림에서 직접 이용할 수 없기 때문에 별도의 모델이 필요하다.
• 따라서 이번 영향 분석 모델은 기본 데이터에서 실제로 사용할 수 있는 것보다 더 많은 입력을 가정하기 때문에 불완전하다.
• 네트워크의 추세는 시간이 지남에 따라 진화할 수 있으며 가장 관련성이 높은 영향도 시간이 지남에 따라 변할 수 있다.
• 소셜 스트림과 관련해 영향 분석 모델을 데이터 중심 또는 콘텐츠 중심으로 만드는 것이 중요하다.
• 소셜 스트림이 표현되는 관점에서 관련 키워드 집합을 선택해 접근 방식이 국소적으로 민감해지면 이러한 키워드의 흐름을 네트워크에서 추적해 다양한 행위자가 현재 주제에 따라 서로 어떻게 영향을 미치는지 결정할 수 있다.
  • 하나의 키워드를 선택한 후 네트워크 구조를 통한 전파는 기본 흐름 경로로 분석된다.
  • 유효한 흐름 경로는 동일한 키워드를 순차적으로 트윗하는 행위자 시퀀스이며, 행위자 순서는 소셜 네트워크 링크로 연결된다.
  • 예를 들어 그림 10.12에 표시된 네트워크에서 다양한 경로를 따르는 해시태그 #baseball 및 #sammysosa의 흐름은 소셜 네트워크에서 리트윗의 결과이다.
    
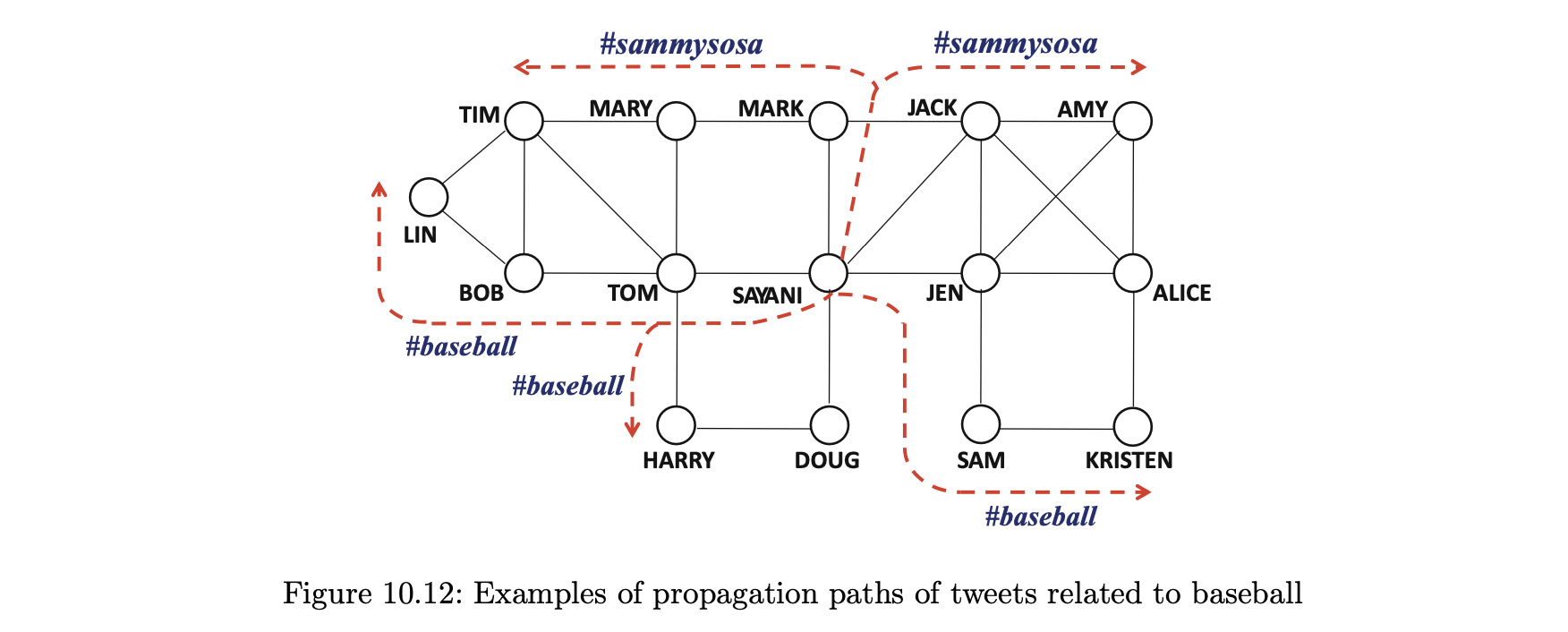
    • 이 경우 사야니는 야구의 특정 주제에 대한 영향력 있는 트위터임을 알 수 있으며, 이 제주에 대한 그녀의 트윗은 종종 다른 참가자들에게 선택될 만큼 권위 있는 것으로 간주된다.
    • 그러나 해시 태그가 야구와 무관한 다른 주제와 관련이 있다면, 동일한 패턴을 가지고 있더라도 사야니는 야구의 특정 컨텍스트에서 영향력을 행사한다고는 볼 수 없을 것이다.
  • 영향력 있는 배우들은 그러한 경로의 초기 부분에서 자주 발생할 것이기 때문에 자주 발생하는 경로를 결정해 다양한 캐스케이드의 중요한 진원지를 결정할 수도 있다.