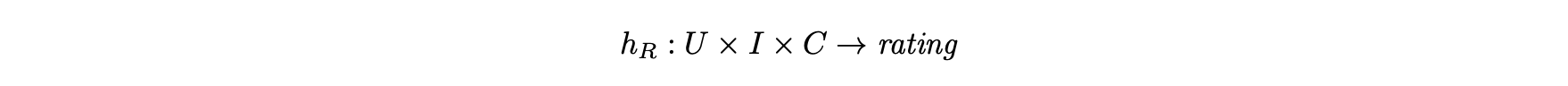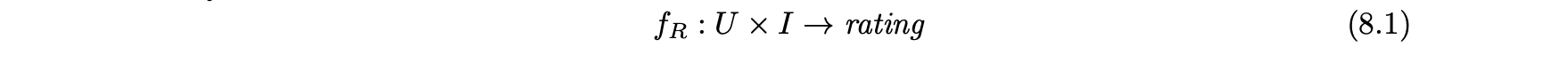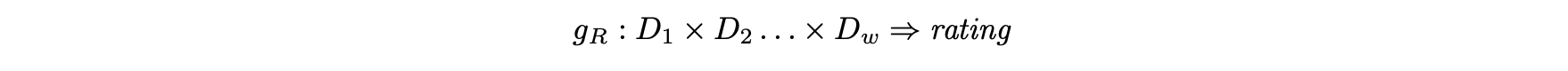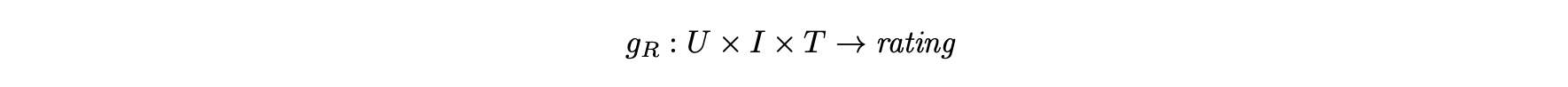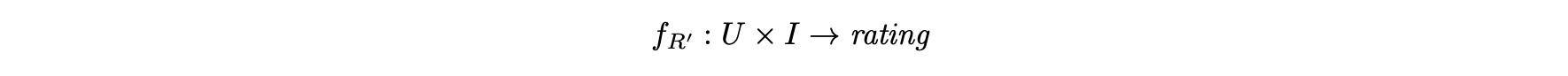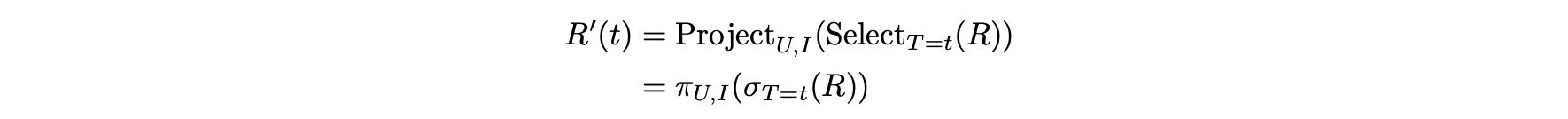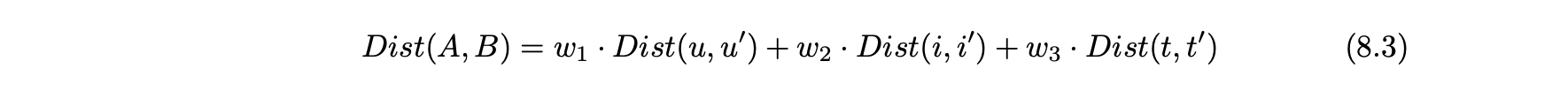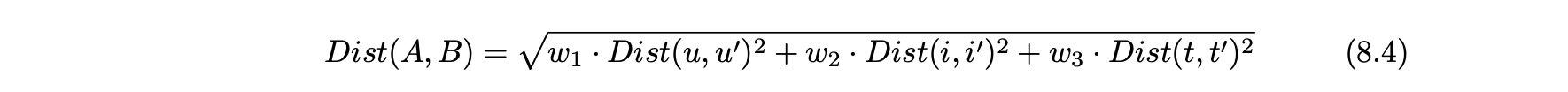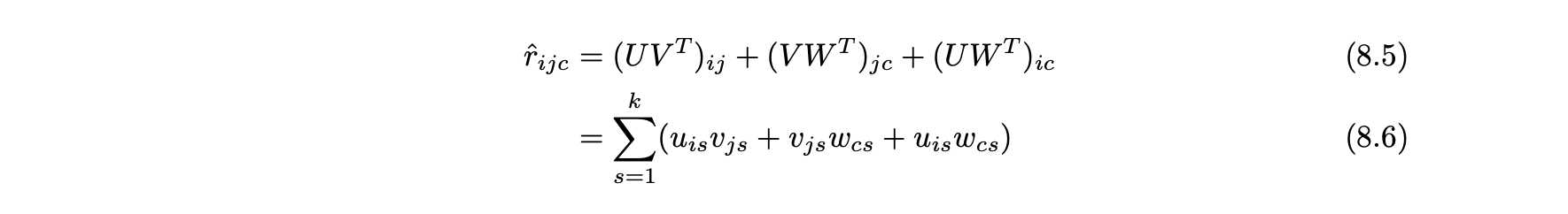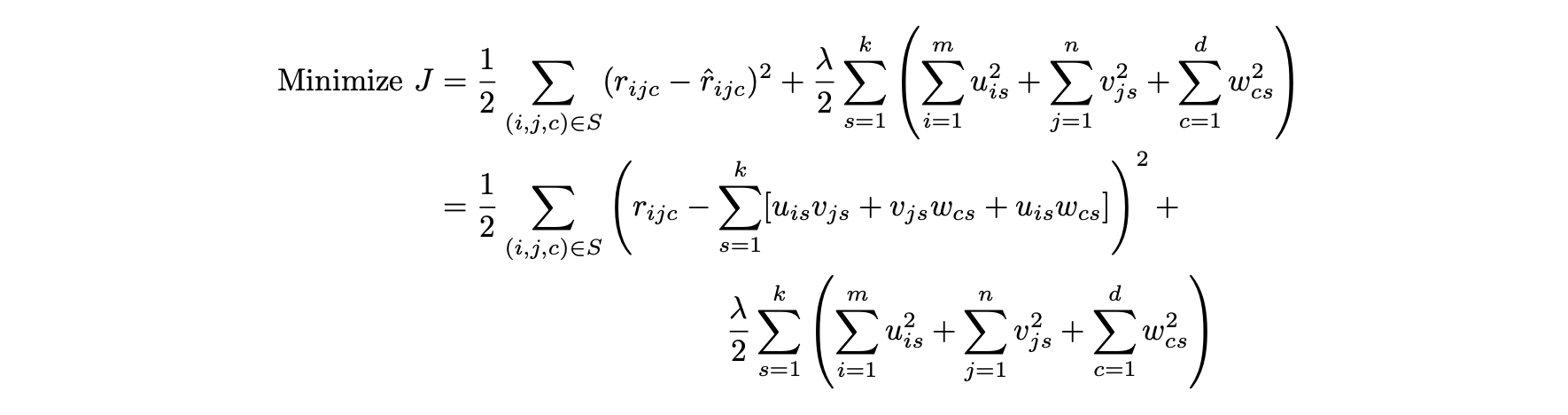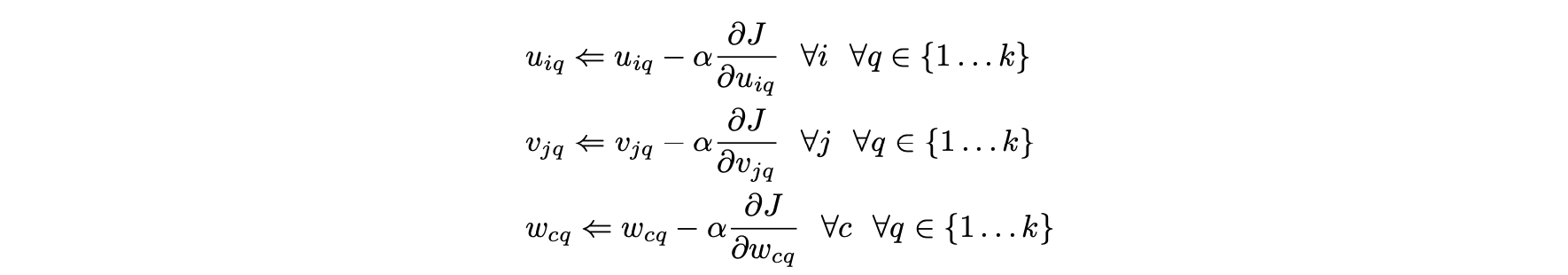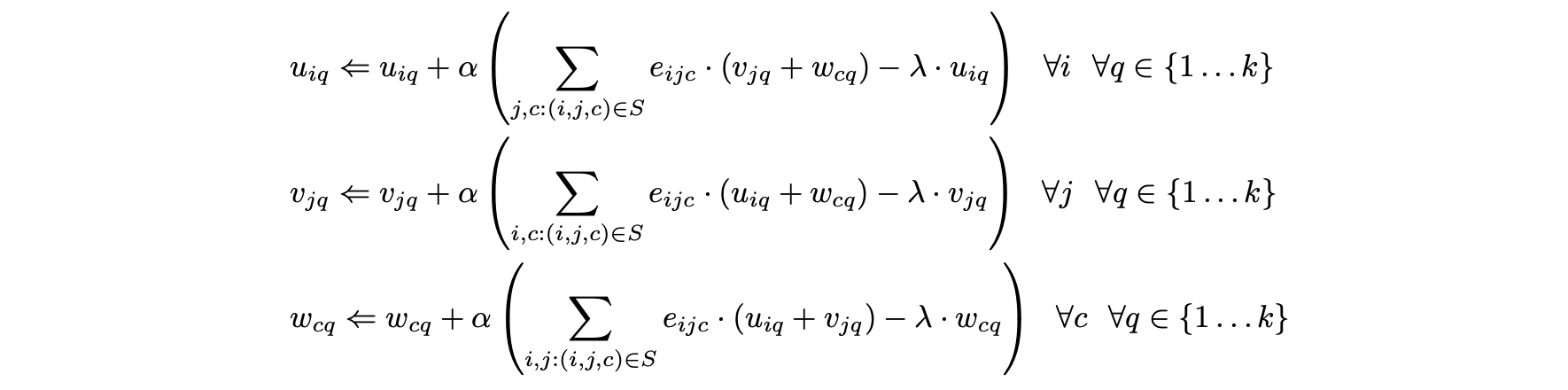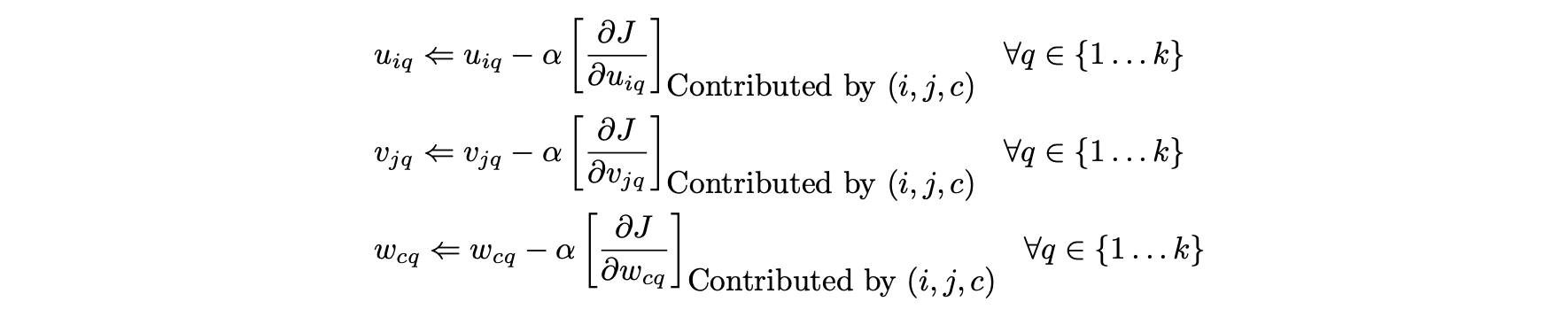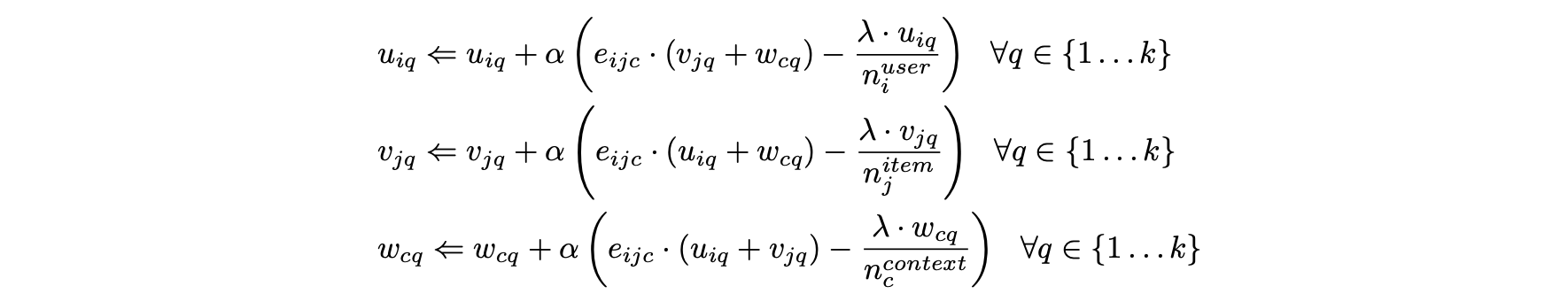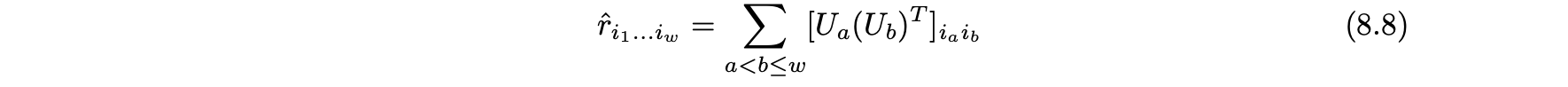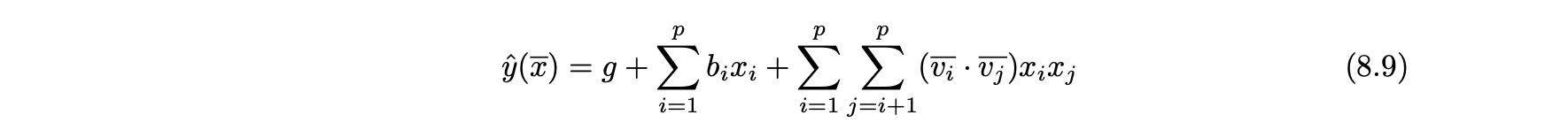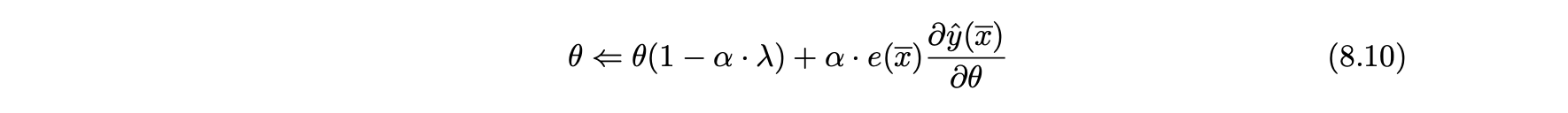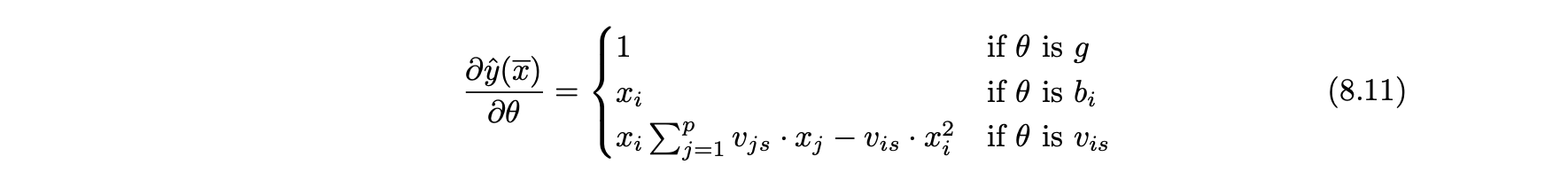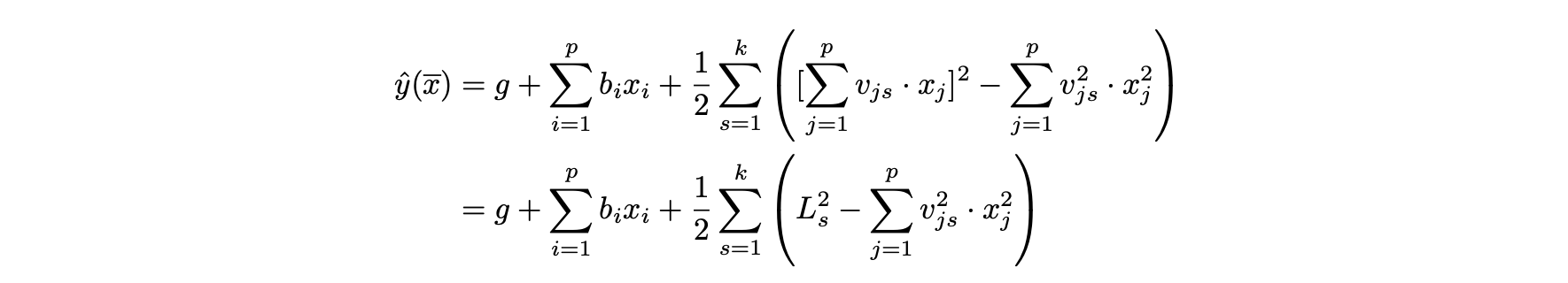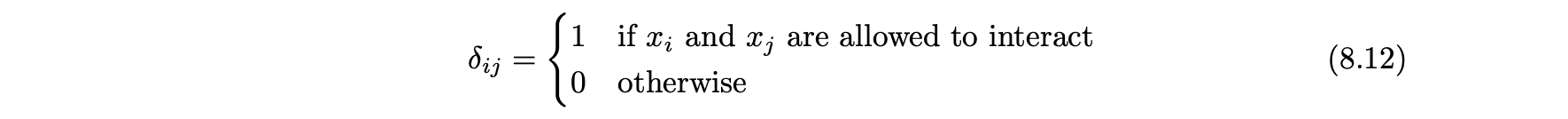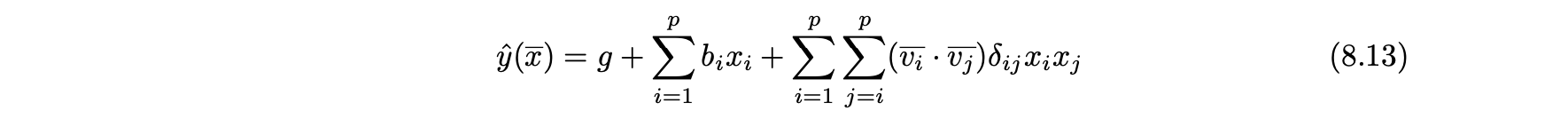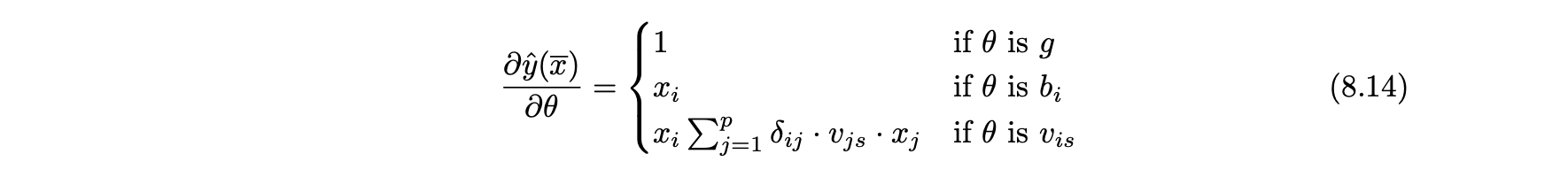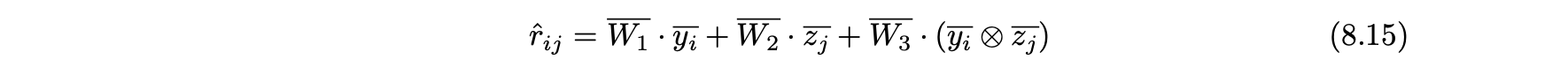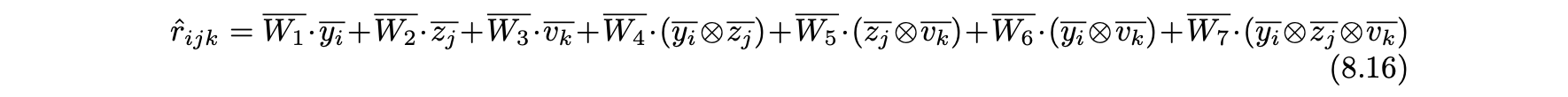📌 개요

• 컨텍스트에 맞는 추천 시스템은 추천이 만들어지는 특정 컨텍스트를 정의하는 추가 정보에 맞게 추천 결과를 조정한다.

컨텍스트의 몇 가지 예는 다음과 같다.

1. 시간 : 추천은 평일, 주말, 공휴일 등과 같은 시간의 여러 측면에 의해 영향을 받을 수 있다.
 Ex> 의류 추천에 있어서 여름과 겨울의 추천은 다를 수 있다.
2. 위치 : GPS 지원이 되는 휴대전화의 인기가 증가함에 따라 위치에 따른 추천의 중요성은 증가하고 있다.
 Ex> 여행하는 사용자는 자신의 지역의 레스토랑을 추천받고 싶어 할 수 있다.
3. 사회 정보 : 추천의 관점에서 사회적 맥락은 중요하다.
 Ex> 사용자는 부모님과 영화를 보는지, 남자친구와 영화를 보는지에 따라 다른 영화를 볼 수도 있다.

사용자의 컨텍스트는 다양한 방법으로 찾을 수 있다.

1. 암시적 수집 방법론은 예를 들어 휴대폰의 GPS 수신기는 고객의 위치를 나타내고 거래 시간 기록은 시간을 의미한다.
2. 명시적 학습의 경우 설문 조사 또는 기타 수단을 통해 수집한다.
3. 데이터 마이닝 및 추론 도구

• 컨텍스트 인식 시스템에서는 C라는 집합 안에 컨텍스트 가능성의 추가 집합이 있다.
  • 컨텍스트는 더욱 세련되고 정확한 추천 결과를 내기 위해서는 반드시 포함돼야한다.
  • 따라서 컨텍스트에 맞는 추천 시스템에서 U x I x C의 가능성은 평점에 매핑된다.
  • 사용자, 항목 및 컨텍스트를 평점에 매핑하는 함수는 다음과 같이 작성할 수 있다.
    
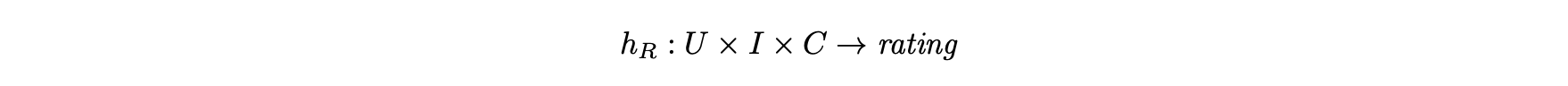
  • 이 경우 평점 데이터 R은 사용자, 항목 그리고 컨텍스트에 대응하는 3차원 평점 데이터 큐브다.
  • 추천은 여러 컨텍스트 차원을 가질 수 있으며 이 경우 다차원 큐브가 생성된다.

📌 다차원 접근법

• 추천에 있어서 전통적인 문제는 사용자-아이템 조합에서 평점에 이르는 매핑 함수를 학습하는 것으로 볼 수 있다.
  • 해당 함수는 다음과 같이 표현할 수 있다.
    
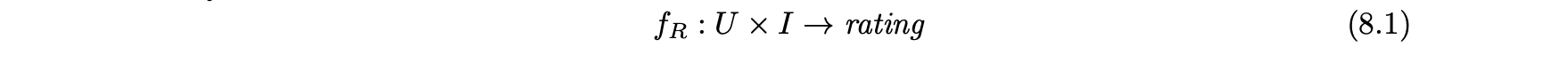
• 다차원 접근 방식의 경우 평점에서의 문제는 서로 다른 차원 값 w 집합을 평점에 매핑하는 것으로 간주한다.
  
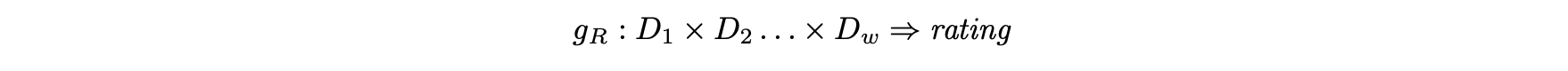
  • 이 경우 2차원 사용자-아이템 조합이 기존 설정의 평점에 매핑되는 것처럼 평점 데이터 R에는 평점에 매핑되는 다양한 차원이 포함돼 있다.
  • 이렇게 하면 2차원 행렬이 아닌 w 차원 큐브가 생성된다.
• 평점 함수 gR은 인수가 w 차원 수와 같은 부분 함수로 정의된다.
• 그림 8.1의 예에서 평점함수 gR은 오후 9시에 영화 <터미네이터>를 시청할 때 사용자 데비이드가 부여한 평점을 나타낸다.
  
  • 컨텍스트는 사용자의 속성, 아이템의 속성, 사용자-아이템 조합의 속성 또는 완전히 독립된 속성일 수 있다.
  • 사용자 및 아이템에 각각 할당된 개별 차원과 마찬가지로 각 컨텍스트에 별도의 차원이 할당된다.

📖 계층 구조의 중요성

• 계층 구조는 집계된 분석을 수행할 수 있는 다양한 수준의 추상화를 제공하기 때문에 컨텍스트에 민감한 추천 시스템에서도 유용하다.
• 집계된 분석을 수행하기 위해 차원의 일부 또는 전부가 계층 구조와 연관된 계층이 있다고 가정한다.

<예시>
1. 위치 차원에는 도시, 주, 지역, 국가 등과 관련된 계층 구조가 있을 수 있다.
2. 인구통계학적 정보가 사용자와 연결된 경우 연령이나 직업과 같은 인구통계학적 계층을 정렬할 수도 있다.
3. 항목 차원은 북미 산업 분류 시스템과 같은 표준 산업 계층 구조를 사용할 수 있다.
4. 시간 등의 차원은 시간, 일, 주, 월 등과 같은 다양한 세분화된 게층 구조 순서에서 나타낼 수 있다.

• 분명히 사용자는 사용할 계층 구조에 대해 미리 신중하게 선택해야 하므로 지정된 적용 사례에서 가장 관련성이 뛰어난 분석이 수행될 수 있다.
• 사용자, 항목 및 시간에 대한 가능한 계층 구조의 예이다.
  
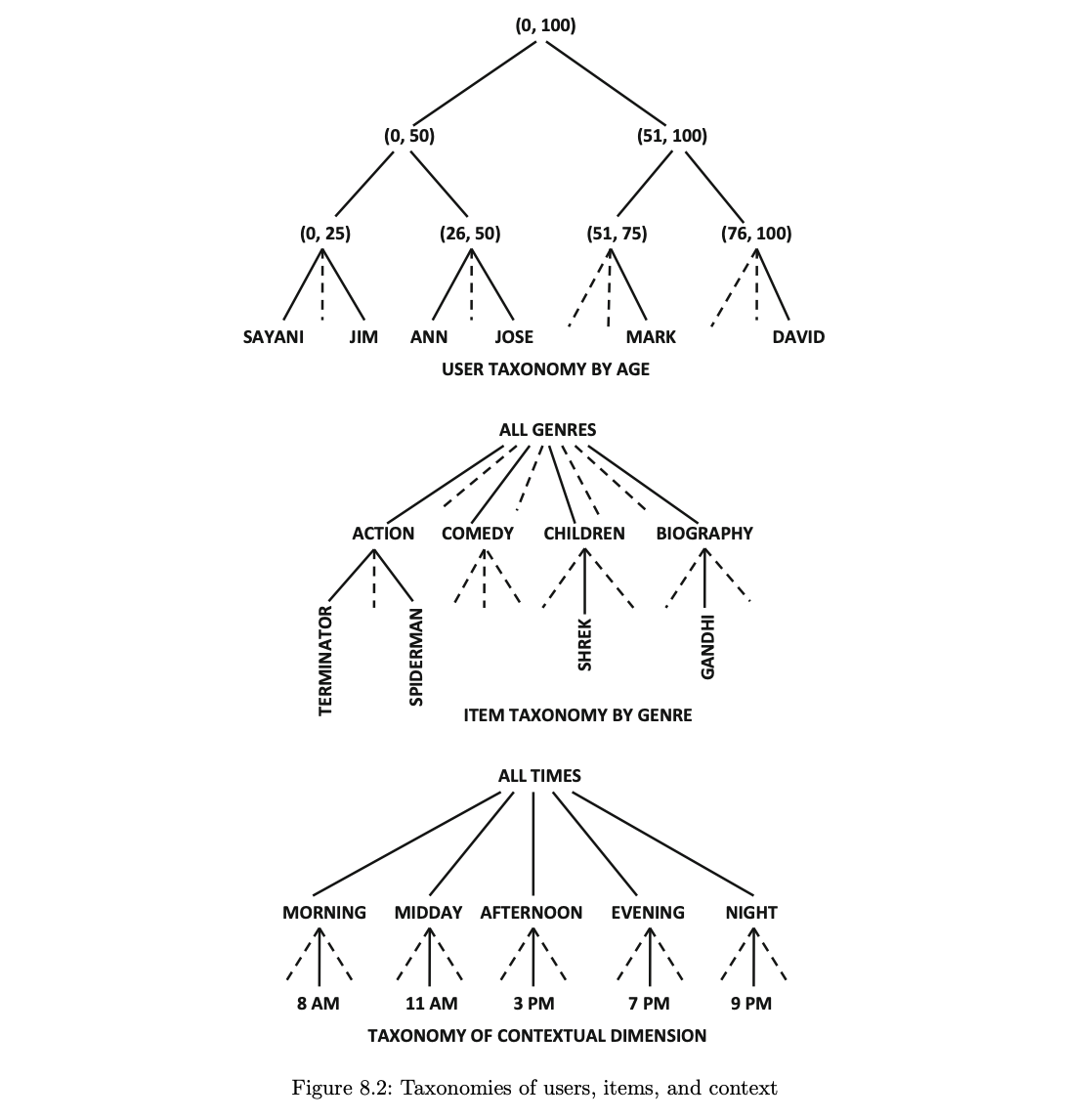
  • 이러한 계층 구조를 사용하면 gR(데이비드, 터미네이터, 오후7시) 대신 gR(데이비드, 터미네이터, 저녁)과 같은 더욱 집계된 쿼리를 만들 수 있다.
  • 이 쿼리는 언제든지 시청되는 액션 영화에 대한 데이비드의 평균 평점을 추청한다.
  • 계층 구조는 컨텍스트 관점에서 뿐만 아니라 사용자 및 항목 차원에 대한 계층적 분석의 관점에서도 유용하다.
    Ex> 데이비드와 같은 특정 사용자에 초점을 맞추기보다는 연령 범위[20,30]의 사용자 수를 집계할 수 있다.
• 여기서 주요 문제는 부분적으로 함수로 정의된 원본 데이터 큐브에서 평점이 완전히 관찰되지 않는다는 것이다.
  • 대부분의 경우 평점은 계층 구조의 하단 수준에서 매우 드문 방식으로 지정된다.
  • 경우에 따라 관찰된 평점을 더 높은 수준으로 지정할 수도 있다.
  • 중요한 단계는 계층 구조의 모든 수준에서 누락된 평점을 추정하는 것이다.

컨텍스트 추천 사항을 수행하기 위한 세 가지 기술 범주

1. 컨텍스트 사전 필터링 : 관련 컨텍스트에 해당하는 평점 세그먼트가 미리 필터링된 후 관련 평점 세그먼트를 사용해 대상된 추천을 만든다.
2. 컨텍스트 사후 필터링 : 추천이 전체 글로벌 평점 집합에서 먼저 수행된 후 순위 추천 목록은 시간적 컨텍스트를 사용해 사후 처리 단계로 필터링 된다.
3. 컨텍스트 모델링 : 컨텍스트 정보는 사전 필터링 또는 사후 필터링 단계가 아니라 예측함수에 직접 통합한다.

📌 컨텍스트 사전 필터링 : 감소 기반 접근 방식

• 컨텍스트 사전 필터링은 감소라고도 한다.
• 감소 기반 접근법에서 w 차원 추정 문제를 2차원 추정 집합으로 줄이는 것이다.
• 세 속성은 사용자(U), 영화 항목(I), 시간(T)이며 이러한 경우 평점 함수는 다음과 같이 정의된다.
  
  • 데이터 집합 R은 이 경우 3차원 큐브이다.
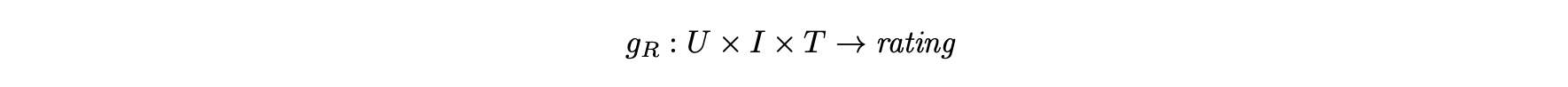
• 매핑은 다음과같이 기존의 2차원 추천시스템을 고려한다.
  
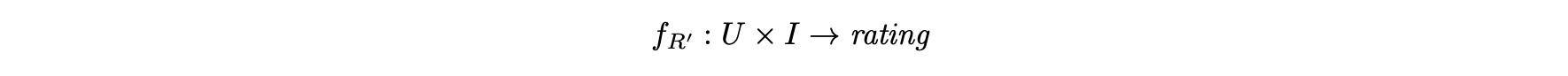
• 3차원 예측 함수는 3차원 평점 행렬의 감소된 미분을 사용해 2차원 예측함수의 관점에서 표현될 수 있다.
  • 시간 t에서 이 작업은 표준 데이터베이스 작업 쌍으로 R에서 2차원 평점 행렬 R'(t)를 파생해 수행한다.
    
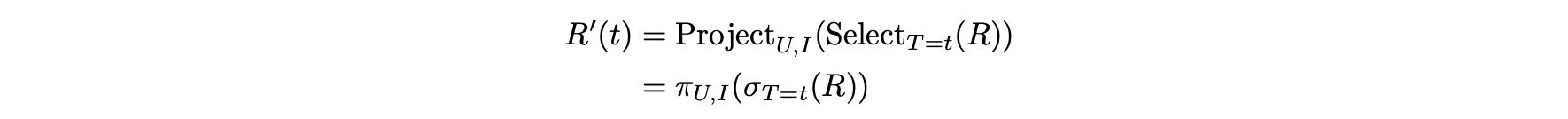
  • 행렬 R'(t)는 먼저 시간이 t로 고정된 채 평점을 선택한 다음 사용자 및 항목 차원을 투영해 가져온다.
  • 2차원 슬라이스는 기존의 협업 필터링 알고리듬에 사용할 수 있는 사용자-항목 행렬을 만든다.
• 이러한 접근 방식을 사용해 오후 9시에 고정된 컨텍스트를 평점 예측에 활용할 수 있다.
  
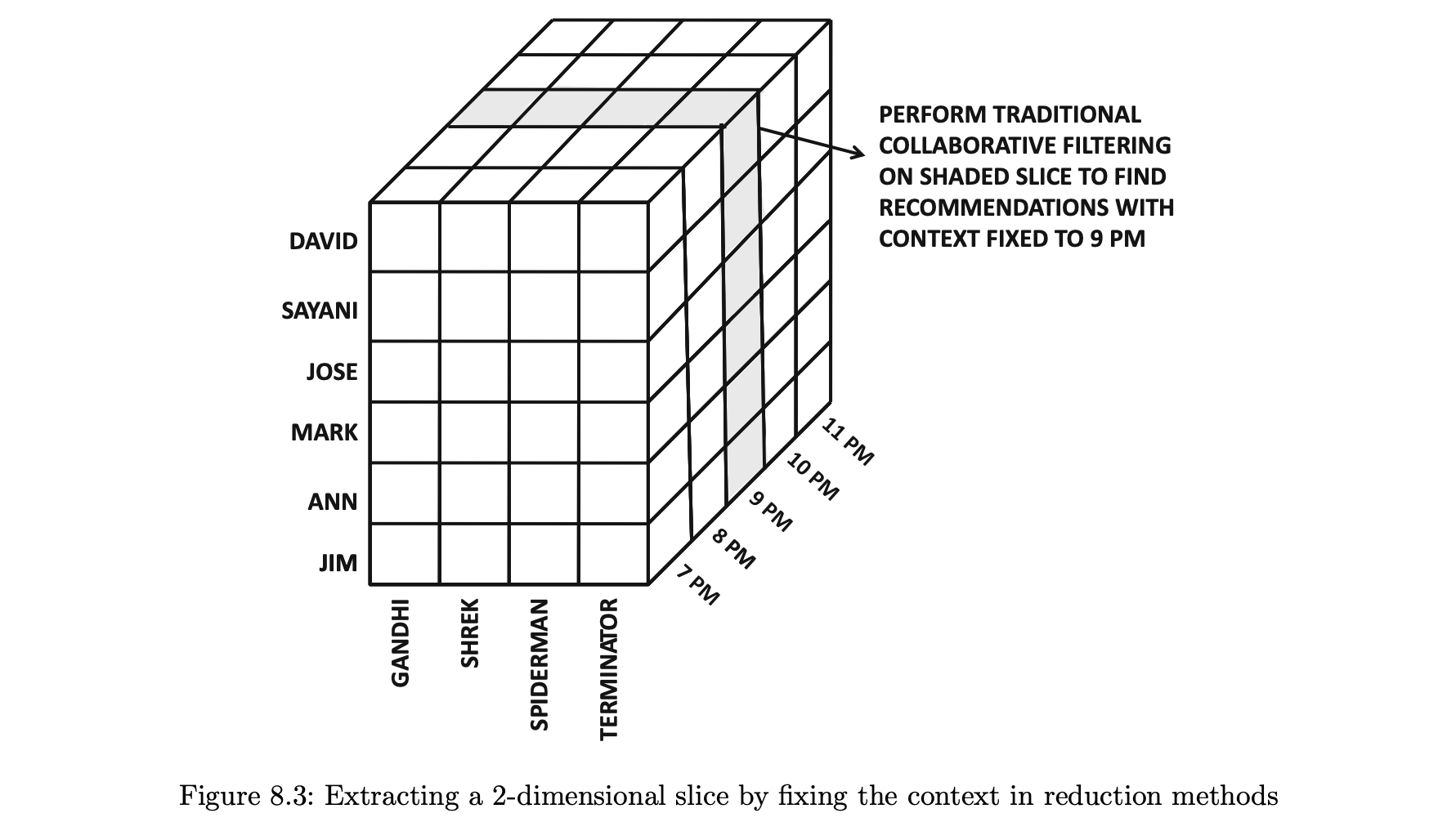
  • 고정되지 않은 두 차원을 주요 차원이라고 하는 반면,
    다른 차원은 컨텍스트 차원이다.
• 평점의 작은 하위 집합인 지정된 슬라이스만이 사용되므로 정확한 추천을 위한 충분한 평점이 없는 경우가 있다.
  • 이러한 경우 t에서 평점을 다른 이웃 시간 조각과 집계해 보다 정확한 추천을 만들 수 있다.
  • 예를 들어 t = 9PM을 사용하는 대신 저녁 7시부터 오후 11시까지 모든 t값을 사용한 다음 이러한 조각의 평점을 평균해 결과 행렬을 만들 수 있다.
  • 컨텍스트를 사용해 선택된 평점과 관련된 평점에 대해서만 협업 필터링을 수행하기 때문에 대부분 향상된 정확도를 볼 수 있다는 장점이 있다.
  • 평점의 수를 증가하기 위해 평균을 사용하는 것은 매번 가능한 것이 아니며, 희소성 문제는 여전히 많은 경우 남아있다.
    또한 사용 가능한 평점이 적을수록 오버 피팅 가능성이 높아진다.
• 글로벌 방법론 : 컨텍스트 변수의 이웃 값에 대해서 평균을 내는 방법론의 극단적인 일반화이다.
  • 글로벌 방법론은 지역화된 컨텍스트 슬라이스를 사용하는 방식보다는 관련도가 떨어지지만 평균 슬라이스에서 더 많은 평점을 사용할 수 있다.
  • 두 대안 간의 정확도 비교는 관련성과 희소성 사이의 절충의 특성에 따라 달라진다.

📖 앙상블 기반 개선 사항

• 앙상블 기반 방법의 목표는 로컬 또는 글로벌 행렬이 바라보는 평점 행렬의 부분에 따라 둘 중 하나가 사용될 수 있다.
• 최상의 모델을 선택하는 대신 모델을 학습시키기 위해 최상의 데이터 세그먼트를 선택하도록 접근 방식을 조정해야 한다.
• 테이블은 가장 높은 정확도를 얻기 위해 사용하는 가장 좋은 일반화를 포함하는 각 위치-시간 가능성으로 만들어지며, 이는 학습 데이터에 대한 교차 검증을 이용해 결정할 수 있다.
• 이 방법론의 한 가지 문제는 컨텍스트별 가능성의 수가 크다면 비용이 매우 클 수 있다는 것이다.

📖 다단계 추정

• 경우에 다라 사용자가 계층 구조의 상위 수준에서 평점을 선정했을 수 있다.
• 기본 아이디어는 낮은 수준에서 관찰되고 예측된 평점의 계산된 평균이 더 높은 수준에서 관찰된 평점과 최대한 근접하로도록 평점을 할당하는 것이다.
• 주요 주의 사항은 과적합을 방지하기 위해 충분한 수의 평점을 사용할 수 있어야 한다는 것이다.

📌 사후 필터링 방법론

• 사후 필터링에서 필터링 단계는 데이터 집합의 컨텍스트 정보를 무시하는 글로벌 협업 필터링 알고리듬을 적용한 후 얻은 출력에 필터링 단계가 적용된다.
• 사후 필터링 방법론에서 컨텍스트 정보는 무시되고 글로벌 2차원 평점 행렬이 모든 컨텍스트적 가능 값에 대한 조합된 평점으로 만들어진다.

사후 필터링 방법론 두 단계

1. 추천은 전통적 협업 필터링 모델을 데이터 전체에 적용하면서 생성된다.
따라서 첫 번째 단계에서는 컨텍스트가 무시된다.
2. 컨텍스트는 추천 목록을 조정하거나 필터링하는 데 사용된다.

• 다차원 평점 큐브가 2차원 평점 행렬로 집계될 때 명시적 피드백 행렬의 경우 집계 프로세스는 평점의 평균을 의미하는 반면 암시적 피드백 행렬의 경우 집계 프로세스는 값의 합을 나타낸다.
• 최종 결과는 항상 2차원 행렬이며 이는 기존의 협업 작업 필터링과 유사하다.

사후 필터링 결과 조정 두 가지 방법

1. 관련이 없는 항목을 필터링한다.
2. 기본 컨텍스트를 기반으로 목록의 추천 사항 순위를 조정하는 데 해당한다.

• 두 가지 사후 필터링 모두 형태는 지정된 사용자-항목 조합에 대해 예측 평점수를 조정한다.

📌 컨텍스트별 모델링

• 사전 필터링과 사후 필터링 모두에서 협업 필터링 문제는 2차원 환경으로 축소되며, 사전 처리 또는 사후 처리 중에 컨텍스트 정보를 사용한다.
• 이러한 접근법의 주요 단점은 컨텍스트가 추천 알고리듬에 매우 밀접하게 통합되지 않는다는 것이다.
• 컨텍스트 모델링 방법론은 이러한 가능성을 탐구하도록 설계됐다.
• 기존 모델을 w-차원 환경으로 수정해 추천 프로세스에 컨텍스트 정보를 직접 통합할 수 있다.

📖 이웃 기반 방법

• 사용자, 아이템, 시간에 해당하는 3차원이 존재한다.
• 첫 번째 단계는 사용자, 아이템 및 시간에 대한 거리를 별도로 계산하는 것이다.
• A와 B 사이의 거리는 개별 차원 사이의 가중 거리의 합으로 정의할 수 있다.
  
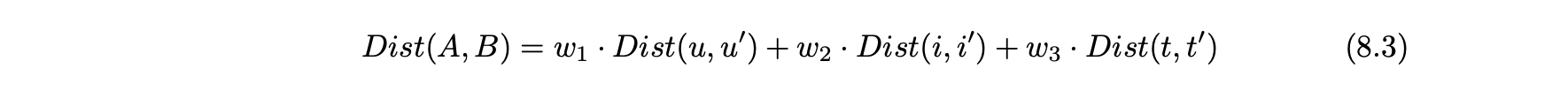
  • 여기서 w1, w2 및 w3은 각각 사용자, 아이템 및 컨텍스트 차원의 상대적 중요성을 반영한다.
• 가중 유클리드 메트릭을 사용할 수 있다.
  
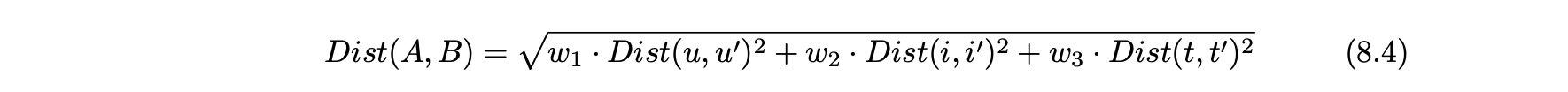
  • 이러한 평점의 가중 평균은 예측 평점이 된다.
• 주어진 사용자 u와 컨텍스트 t에 대한 추천을 수행하기 위해서는 각 아이템에 이 프로세스를 적용한 다음 상위-k개 아이템을 추천해야 한다.

Dist(u,u'), Dist(i,i'), Dist(t,t')를 결정하는 몇가지 방법이 있다.

1. 협업 : 피어슨방법이나 조정된 코사인을 사용해 계산할 수 있다.
2. 콘텐츠 기반 : 차원과 관련된 속성을 사용해 프로파일을 계산한다.
3. 조합 : 협업 필터링 방법과 콘텐츠 기반 측정 값을 결합해 유사도의 더 강력한 측정 값을 얻을 수 있다.

📖 잠재 요인 모델

• 텐서 분해는 2차원 행렬이 아닌 n차원 데이터 큐브를 분해하는 행렬 계수의 일반화로 간주할 수 있다.
• 컨텍스트를 반영하는 기존 표현 방식은 실제로 w 차원 큐브이므로 행렬 인수분해에 특히 적합하다.
• 쌍방향 상호작용 텐서 분해는 다차원 설정에서 잠재 인자 모델의 원칙을 적용하는 다른 단순화된 방법이다.
• R 평점 행렬은 m 사용자, n 항목, d 컨텍스트 차원의 m x n x d 형태의 3차원 평점 큐브다.
  • U는 사용자 벡터 행렬을 나타내고, V는 항목 계수 행렬을 나타내며, W는 컨텍스트 계수 행렬을 나타낸다.
  • 다음 데이터 큐브의 단순화된 예측함수 (i, j, k)의 기본 원리는 사용자, 항목, 컨텍스트 간의 쌍별 상호작용을 기반으로 한다.
    
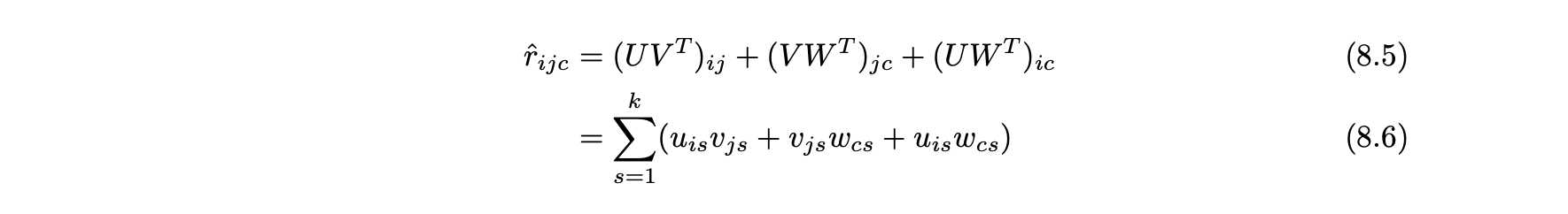
  • 이 예측함수가 잠재 인자 모델의 간단한 일반화임을 쉽게 알 수 있다.
  • 이 예측함수를 사용해 모든 인자 모델과 마찬가지로 최적화 문제를 설정할 수 있다.
• 관찰된 모든 항목에 관한 오류를 다음과 같이 최소화해야 한다.
  
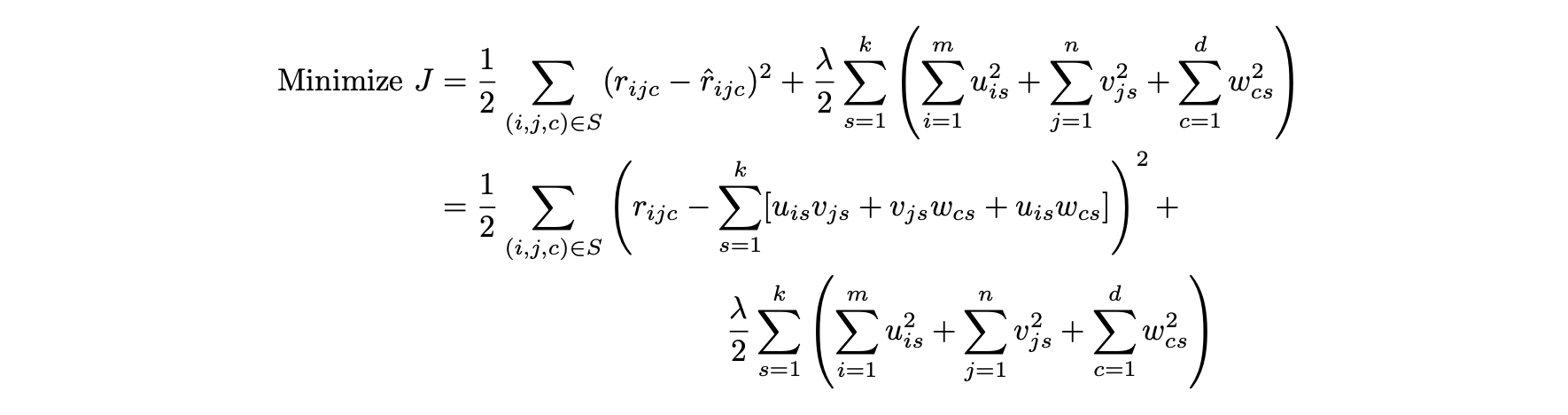
  • 마지막 항은 λ > 0인 정규화 매개변수인 정규화 항이다.
• 경사하강 방법론에 대한 업데이트된 방향을 도출하기 위해 U, V, W의 개별 요소에 대해 J의 부분 미분을 해야한다.
  
  • 여기서 α > 0은 단계 크기다.
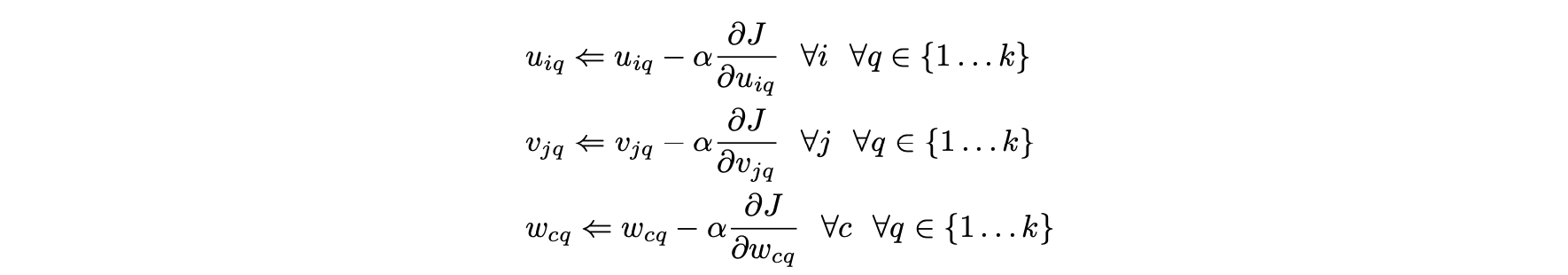
• 기존의 잠재 인자 모델에서와 같이 하강 방향은 관측된 값에 대한 에러이다.
  
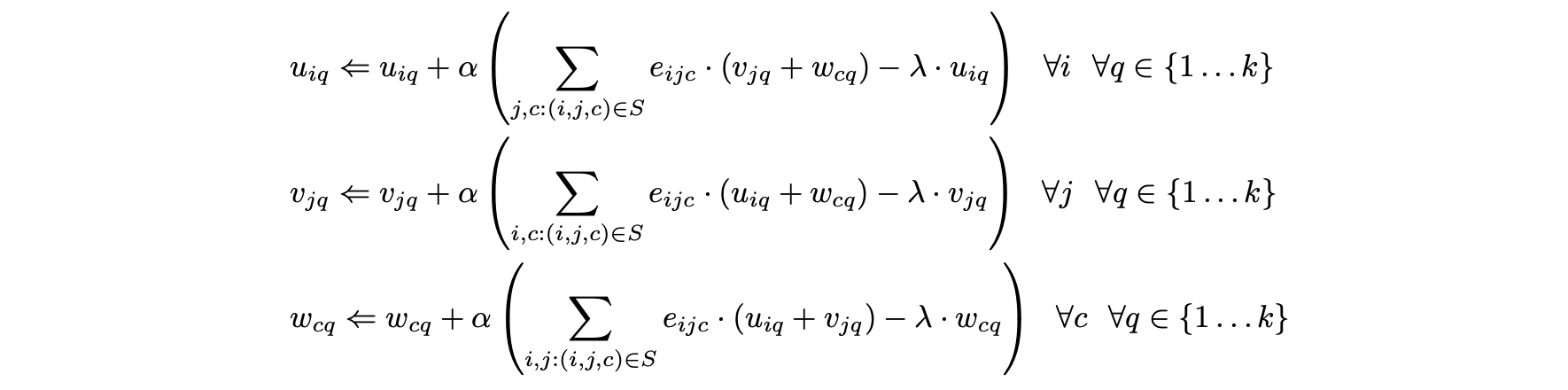
• 더 빠른 대안은 확률적 그라데이션 하강을 사용하는 것이다.
  
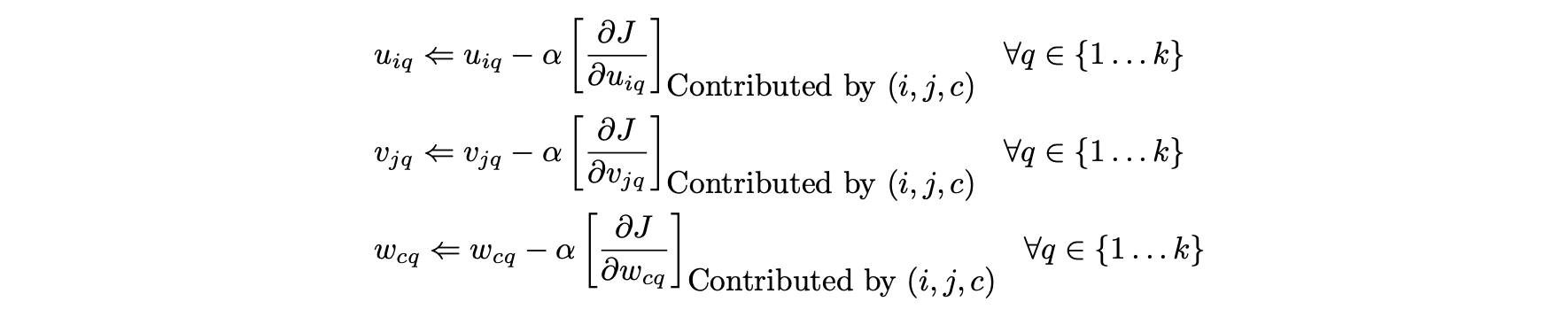
• 이러한 기여를 계산할 때, 다음 단계는 각 지정된 항목의 q번째 잠재 구성 요소
  (1<= q <= k)에 대해 실행될 수 있다.
  
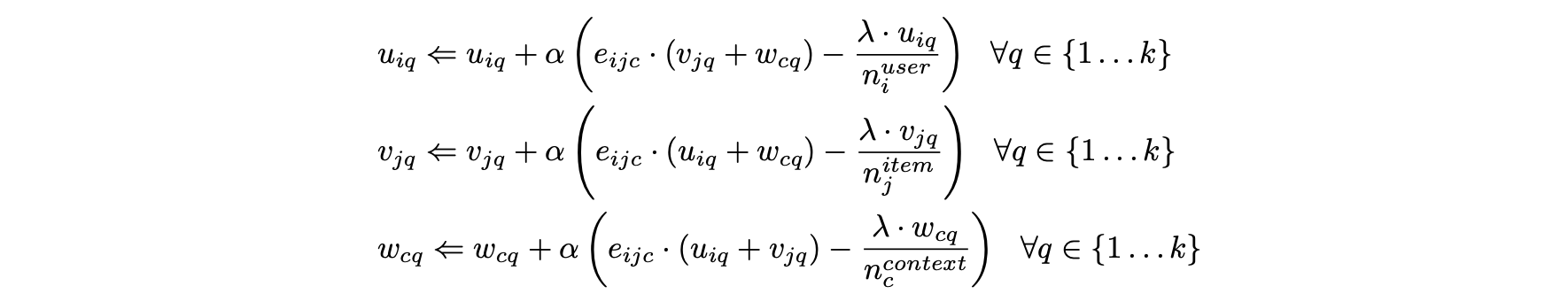
• 이러한 점진적 경사하강 방법론은 U, V, W 행렬을 얻기 위해 수렴하도록 실행될 수 있다.
• 이 방법은 고차 텐서 분해 모델보다 덜 복잡하며, 특히 희소한 행렬에서 잘 작동할 수 있다.
• 이 원리는 w > 3의 w차원 큐브로 확장할 수 있으며, 각각의 크기의 w 잠재 인자 행렬의 관점에서 예측된 평점 값을 표현할 수 있다.
  
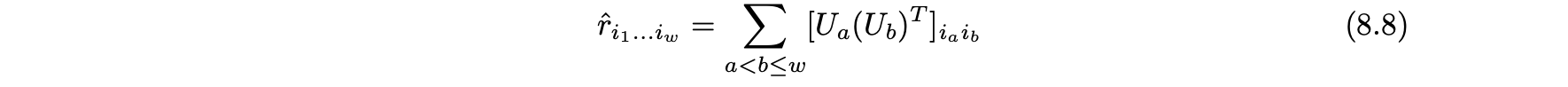
  • 3차원 큐브의 경우와 같이 최소 최적화 문제를 만들 수 있다.
    *표준 경사하강 방법을 사용해 이 문제를 해결할 수 있다.

1. 인수분해 머신

• 이전 절의 잠재 계수 접근 방식은 인수분해 머신(FM)의 특수한 경우로 볼 수 있으며 상당수는 인수분해 머신의 특수한 경우이다.
• 인수분해 머신에서 기본 아이디어는 각 평점을 입력변수 간의 상호작용의 선형 조합으로 모델링하는 것이다.
• 3차원 큐브를 관찰된 평점의 사용자, 항목, 컨텍스트 값에 해당하도록 하는 차원 행 집합 (m + n + d)차원 행 집합으로 변환할 수 있다.
  • 관찰된 평점 수만큼 많은 행이 있다.
• 그림 8.4에서는 그림 8.1에서 데이터 큐브의 5개의 관찰된 평점의 변환을 보여준다.
  
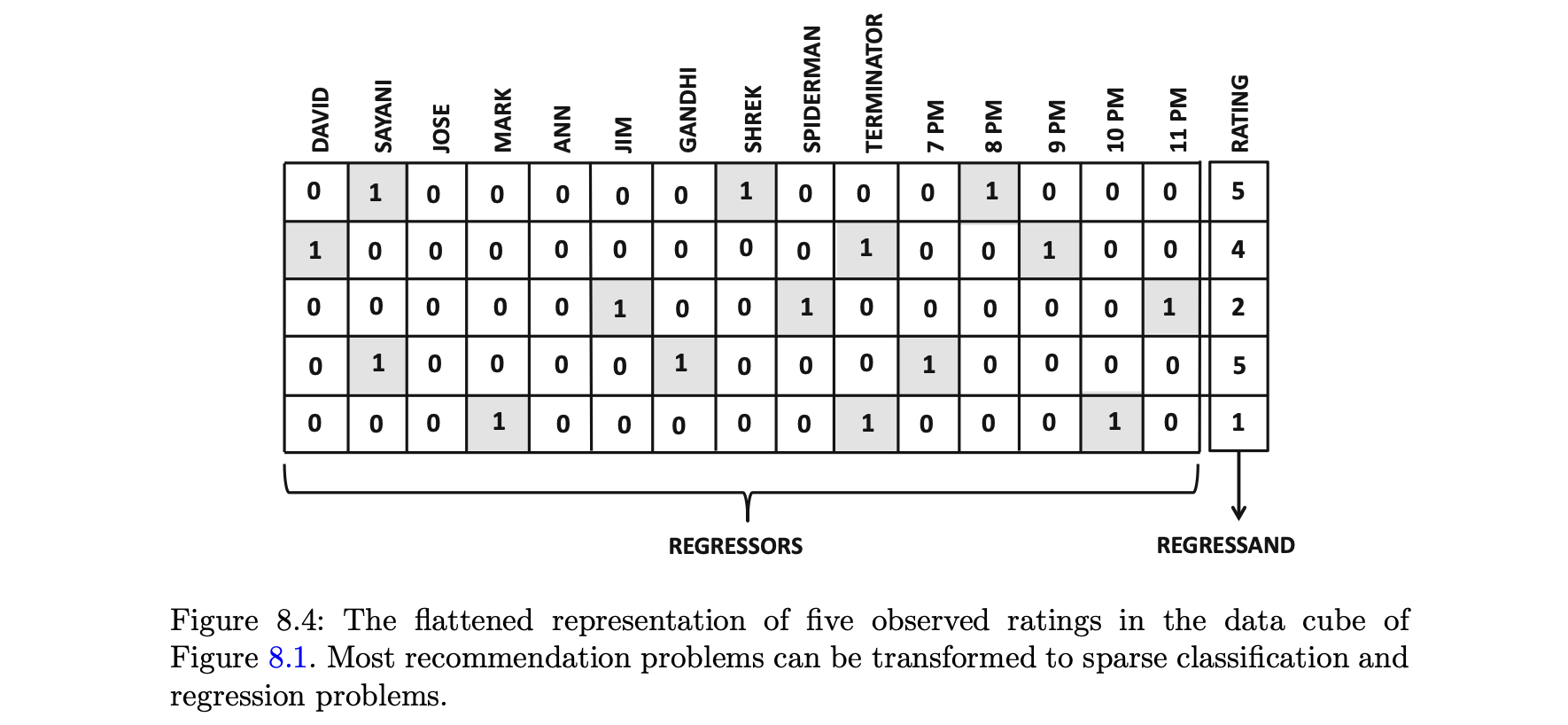
  • 간단한 방법으로 이 변환을 분류 또는 회귀 예측 변수로 사용해야 하지만,
    각 행에 0이 아닌 값이 3개 밖에 없는 이 희소한 데이터의 경우에는 잘 작동하지 않는다.
  • 인수분해 머신은 희소성의 위험에서 해결책을 제시해준다.
• 기본 아이디어는 k차원 잠재 계수를 각 p = (m + n + d) 결정 변수와 연결하는 것이다.
• 2차 계수 인수분해 머신의 예측 평점은 다음과 같은 요소 간의 쌍별 상호작용을 사용한다.
  
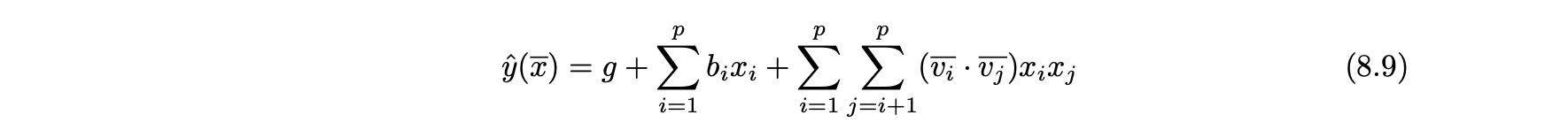
  • i 번째 변수와 연결된 계수 벡터는 v라 하자.
  • i 번째 열에는 b 바이어스가 있으며, 글로벌 바이어스 변수 g가 있다.
  • 학습할 변수는 g, b와 각 벡터 v이다.
  • 상호작용 항의 수는 놀랍도록 크게 생각될 수 있지만, 그들 대부분은 데이터가 희박한 설정에서는 0으로 평가된다.
• 확률적 경사하강법은 상기 파라미터를 추정하기 위해 관찰된 평점을 사용한다.
  
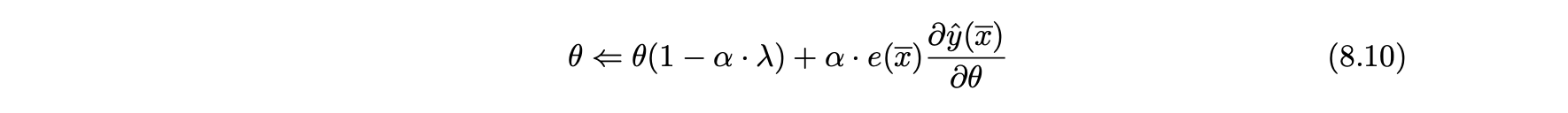
  • 특정 모델 매개변수 θ에 대한 업데이트는 예측 값과 관찰 값 사이의 오류에 따라 달라진다.
  • 여기서 α > 0은 학습 속도이고, λ > 0은 정규화 파라미터이다.
• 업데이트 방정식의 부분 미분은 다음과 같이 정의된다.
  
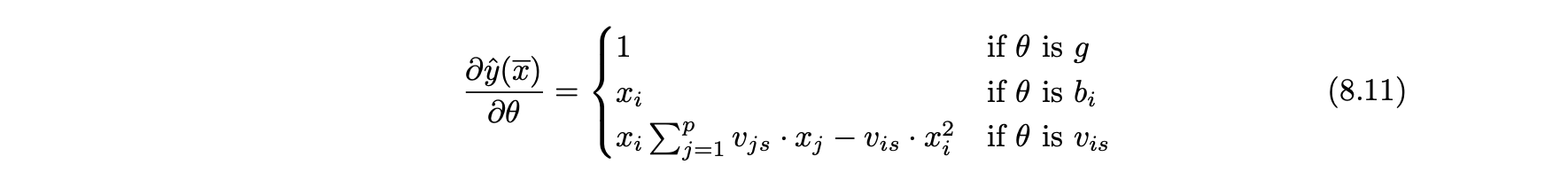
• 식 8.9가 다음과 같이 대수적으로 재배열 될 수 있다.
  

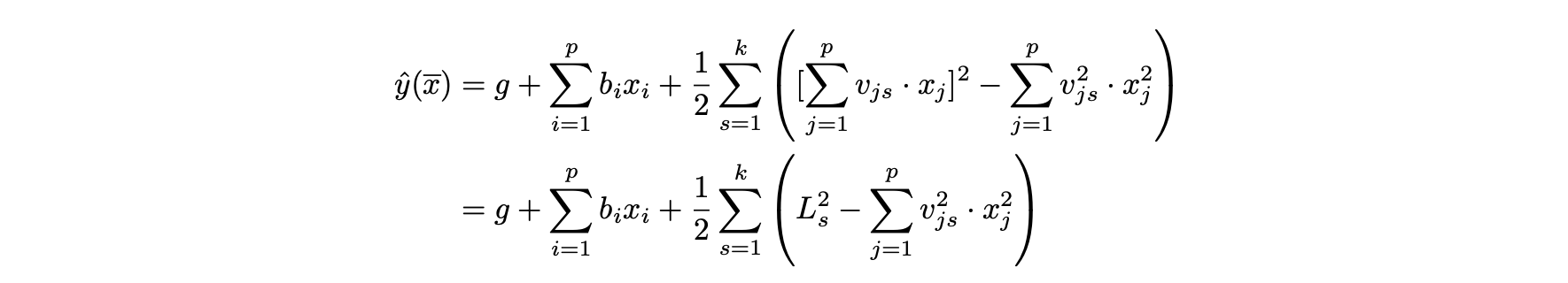
2. 2차 인수분해 머신의 일반화

• 2차 인수분해 머신은 모든 변수쌍이 서로 상호작용한다고 가정하지만 항상 바람직하지는 않을 수 있다.
• 이 설정을 처리하기 위해 상호작용 표시 δ를 정의해 서로 상호작용할 수 있는 변수 쌍을 나타낸다.
  
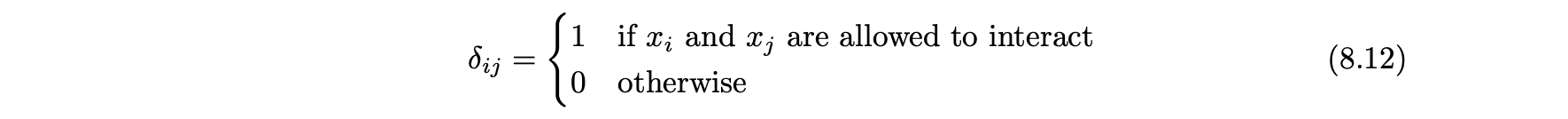
  • 분석가가 변수의 중요한 상호작용 블록에 대해 도메인 지식을 활용할 수 있다.
• 이 표시를 사용해 다음과 같이 식 8.9를 일반화할 수 있다.
  
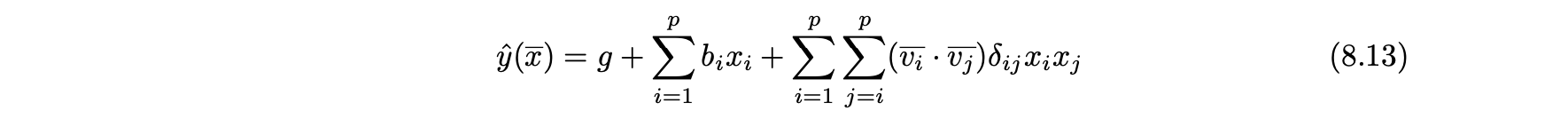
  • 식 8.9와 달리 이 식은 δ가 0이 아닌 경우 xi가 자신과 상호작용할 수 있게 된다.
• 솔루션은 인수분해 머신과 거의 동일하며, 식 8.10의 업데이트 단계는 확률적 경사하강에서 사용할 수 있다.
  
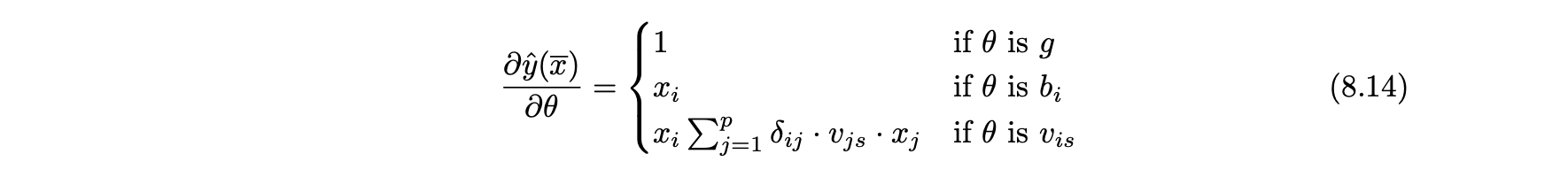
  • 유일한 차이점은 각 모델 매개변수 θ와 관련해 예측 변수의 부분 미분을 수정해야 한다는 것이다.

3. 잠재 파라미터화의 다른 적용 사례

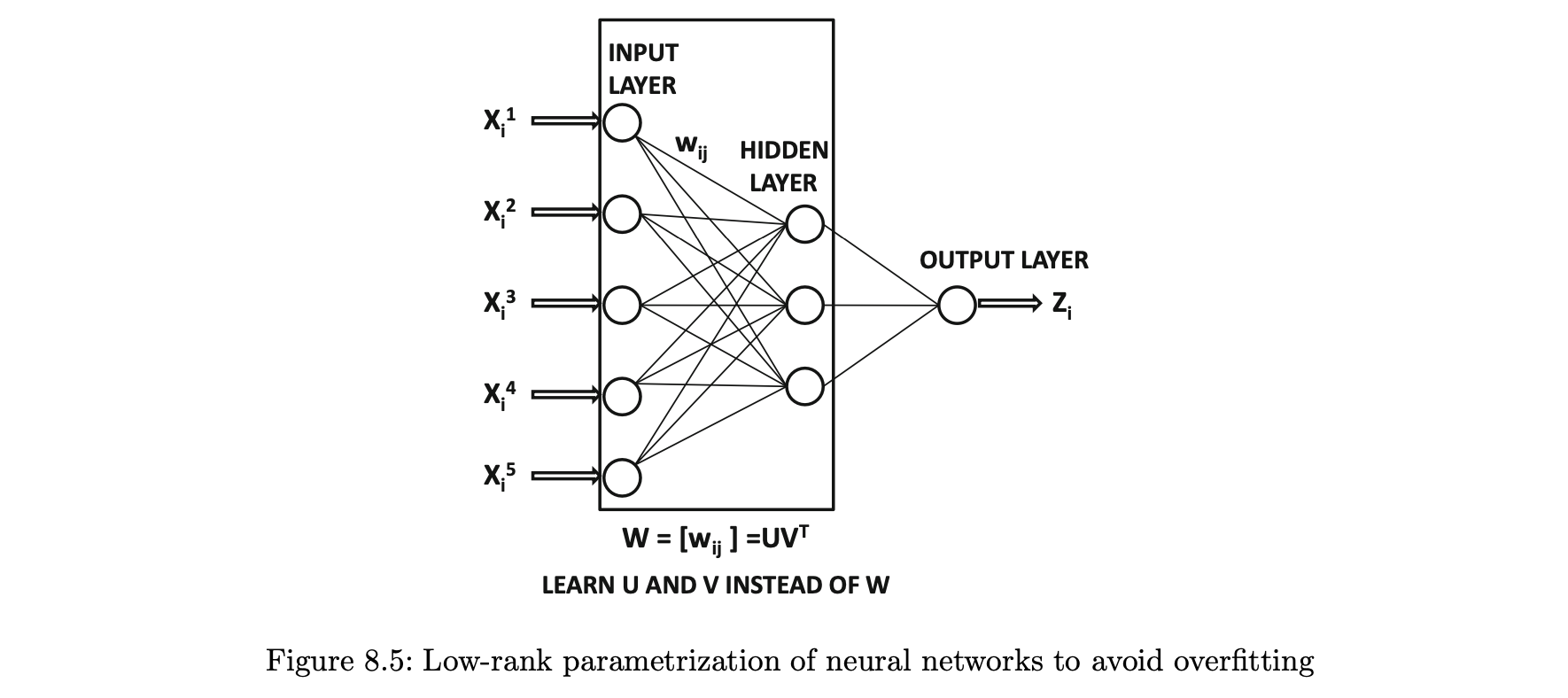
• 기본 아이디어는 신경망의 두 연속층 사이의 가중치 수를 행렬로 나타낼 수 있다.
• 입력 레이어의 크기는 항목 수와 숨겨진 레이어의 크기로 축적되기 때문에 행렬의 크기는 협업 작업 필터링 설정에서 다소 클 수도 있다.
  • W의 크기는 이 두 값의 곱에 의해 정의된다.
• W를 학습하는 대신 U와 V의 매개변수를 학습한다.
  • 이러한 유형의 매개변수 공간의 낮은 순위 감소는 정확도와 실행 시간 면에서 상당한 이점을 가지고 있다.
    

📌 콘텐츠 기반 모델

• 서포트 벡터 머신과 선형 회귀와 같은 다양한 머신런이 모델은 컨텍스트에 예민한 추천 시스템고 함께 사용된다.

컨텍스트 정보를 사용하지 않는 간단한 선형 회귀 모델

• 사용자, 항목 피처, 항목 기능 및 크로네커 교차곱의 선형 기능으로 평점을 추정하는 선형 회귀 모델이다.
  
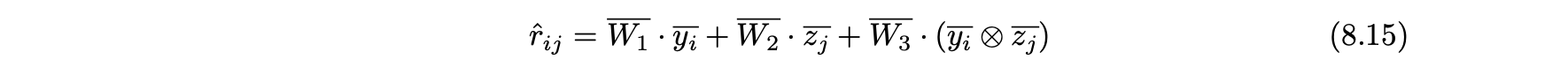
  • W1, W2, W3는 적절한 길이의 선형 회귀 계수 벡터이다.
  • yi은 예를 들어 성별 또는 인종과 같은 사용자 i의 특징 변수 벡터에 해당한다.
  • zj는 예를 들어 영화 장르 및 제작 스튜디오와 같은 항목j의 특징 변수 벡터에 해당한다.
  • (yi x zj)는 사용자 i와 항목 j의 피터 벡터 사이의 크로네커 교차곱에 해당한다.
  • 크로네커 교차곱은 예를 들어 성별 장르, 인종 장르, 성별, 인종의 다양한 가능성과 같이 사용자 i와 항목 j의 기능 값 간의 모든 가능한 교차 제품 조합에 의해 정의된다.
  • 이러한 조합의 값은 1로 설정되며 다른 모든 가능한 조합의 값은 0으로 설정 된다.
  • 관찰된 평점은 모델을 만들고 벡터 W1, W2, W3를 학습하기 위해 학습 데이터로 사용된다.
  • 상호작용 계수는 사용자-항목 피처의 다양한 조합이 모델에 미치는 영향을 알려준다.

컨텍스트 차원에 대한 추가 피처 변수를 도입해 컨텍스트 시나리오에 일반화

• 시간이 컨텍스트 변수로 사용되는 경우를 고려한다.
  • 시간 차원의 k 번째 가능 값과 연결된 피처 변수는 벡터 vk에 의해 표시된다.
• 평점의 예측값은 다음과 같이 피처 변수와 상호작용 변수의 선형함수로 계산된다.
  
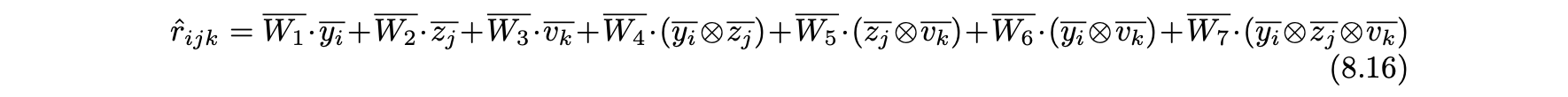
  • 계수를 줄이기 위해 3차원 계수 W7을 0으로 설정할 수 있다.
  • 이러한 모델은 2차원 인수분해 머신과 유사한 형태로 수행되며, 유사한 경사 하강법 방법론을 사용할 수 있다.
• 이 일반적인 접근 방식은 실제로 회귀 기반 모델뿐만 아니라 기존 머신러닝 모델과 함께 사용할 수 있다.