Python

파이썬의 heapq 모듈로 힙 자료구조 사용하기
[Python] heap과 heapq 모듈
Python heapq 모듈 사용법

• heapq 모듈은 이진 트리 기반의 최소 힙 자료구조를 제공
  • 예시: [3, 6, 4, 8, 2, 1]
  • 이 배열에서 가장 작은 정수를 구하기 위해서는 for문을 돌려 시간 복잡도는 O(N) 이 될 것
  • 하지만 힙은 logN 의 속도로 더 빠르게 찾을 수 있게 도와줌

heap

• 힙은 특정한 규칙을 가지는 트리
  • 최댓값과 최솟값을 찾는 연산을 빠르게 하기 위해 고안된 완전 이진 트리를 기본으로 함

• 완전 이진 트리의 일종으로 우선 순위 큐를 위해 만들어졌음
  • 여러 개의 값 중에 최대값과 최솟값을 빠르게 찾을 수 있음
  • 힙 트리에서는 중복된 값도 허용
    • 이진 탐색 트리에서는 허용하지 않음

Tip! 추가 내용

• 힙 속성
  • A가 B의 부모 노드이면 A의 키값과 B의 키값 사이에는 대소 관계가 성립

• 최소 힙 ( Min Heap )
  • 부모 노드의 키값이 자식 노드의 키값보다 항상 작은 힙
• 최대 힙 ( Max Heap )
  • 부모 노드의 키값이 자식 노드의 키값보다 항상 큰 힙

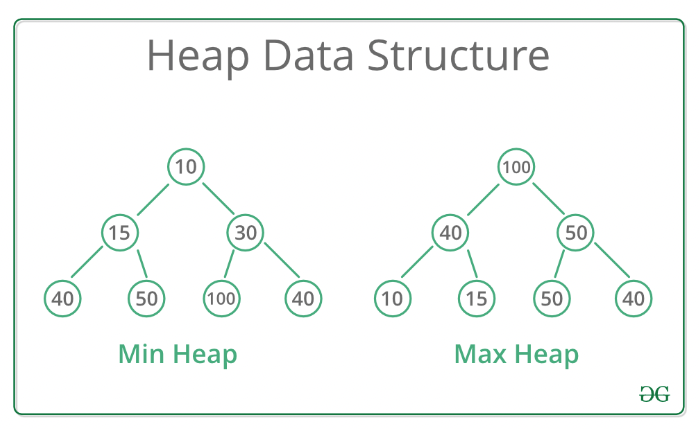
• 힙 속성으로 인해 힙에서는 가장 낮은 ( 혹은 높은 ) 우선순위를 가지는 노드가 항상 루트에 오게 되고 이를 이용해 우선순위 큐와 같은 추상적 자료형을 구현할 수 있음
  • 이때 키값의 대소 관계는 부모자식 간에만 성립하고 형제노드 사이에는 대소 관계가 정해지지 않음

완전 이진 트리

• 마지막을 제외한 모든 노드에서 자식들이 꽉 채워진 이진 트리
  • 힙은 루트가 가장 작은 값인 최소힙과 루트가 가장 높은 값인 최대힙이 있음

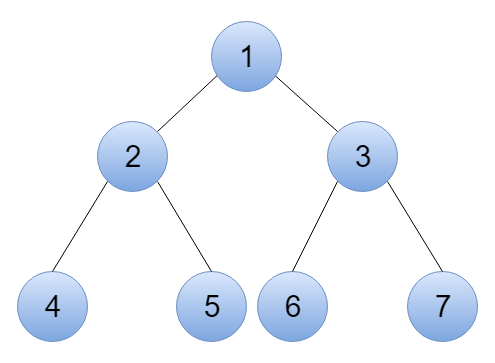
• 루트는 최소값인 1
• 자식은 자신보다 크기만 하면 되기 때문에 왼쪽 ∙ 오른쪽 상관 없음
  • 왼쪽 자식은 부모 인덱스 * 2
  • 오른쪽 자식은 부모 인덱스 * 2 + 1
• push 나 pop 을 실행하면 자식 인덱스와 비교하면서 루트까지 오게 됨

heapq

• 내장 모듈이기 때문에 설치 하지 않아도 됨

import heapq

heap = []

heappush

• 힙에 원소 추가
  • heapq.heppush() 함수를 이용
  • 첫번째 인자에는 원소를 추가할 리스트
  • 두번째 인자에는 추가할 원소

heapq.heappush(heap, item)
heapq.heappush(heap, item2)

print(heap)

>>> [item, item2]

heappop

• 힙에 있는 원소 삭제
  • 가장 작은 원소를 힙에서 제거함과 동시에 그를 결괏값으로 리턴
  • 원소를 삭제하지 않고 가져오고 싶으면 [0] 인덱싱을 통해 접근하면 됨

heap = [1, 2, 3, 4, 5]

heapq.heapppop(heap)

print(heap)

>>> [2, 3, 4, 5]

heapify

• 일반 배열을 힙으로 만들어 줌

arr = [3, 5, 2, 4]

heapq.heapify(arr)

print(arr)

>>> [2, 3, 4, 5]

최대 힙 만들기

• heapq 에서는 최소 힙만 지원
  • 최대 힙을 만들기 위해서는 키 값을 - 로 바꿔줘야 함
  • 키 값을 바꾸는 시간은 O(N) 이고 힙 요소를 얻는데는 O(nlog n) 이라서 시간 복잡도에는 문제 되지 않음

reverse = lambda x: x * -1
max_heap = list(map(reverse, heap))
heapq.heapify(max_heap)
max_heap = list(map(reverse, max_heap))

• 하지만 음수로 바꿨다가 다시 양수로 바꿔야되기 때문에 매우 번거로움
  • 최대 힙을 쓸 때는 최대 힙 클래스를 정의해 만드는 것이 좋음