
Minimum Spanning Tree
Minumum Spanning Tree란?
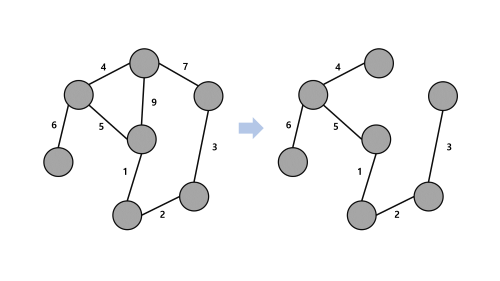
최소 신장 트리는 한 그래프에 존재하는 Spanning Tree 중에서 트리를 구성하는 모든 간선의 가중치 합이 최소인 것을 말합니다.
Spanning Tree?
한 그래프의 서브 그래프 중 그래프의 모든 정점을 포함하고 사이클이 없으며 임의의 두 정점 사이의 경로는 하나만 존재하는 무향 연결 그래프
Prim's Algorithm
Prim's Algorithm이란?
프림 알고리즘은 그래프에서 최소 신장 트리를 찾는 알고리즘으로 Greedy Algorithm 중 하나입니다.
Greedy Algorithm
문제를 해결하는 과정에서 결정이 필요한 매 순간마다 그 상황에서 최적이라고 여겨지는 선택을 하면서 최종 해답에 도달하는 문제 해결 방법
각 선택이 그 상황에선 최적의 선택이더라도 전체 문제에선 최선의 선택이 아닐 수 있기 때문에, 앞의 선택이 이후의 선택에 영향을 주지 않고 각 단계의 선택이 전체 문제에 대해서도 최적인 경우에 사용하는 것이 좋음
프림 알고리즘은 하나의 트리를 점점 키워 나가는 방식으로 최소 신장 트리를 찾습니다.
과정
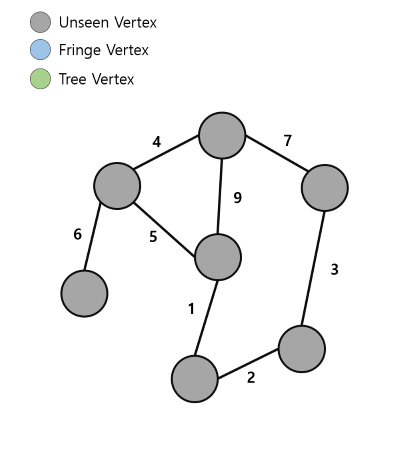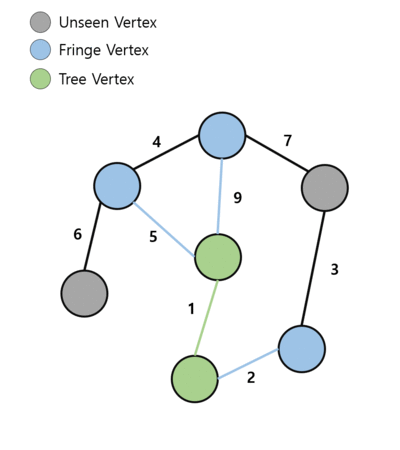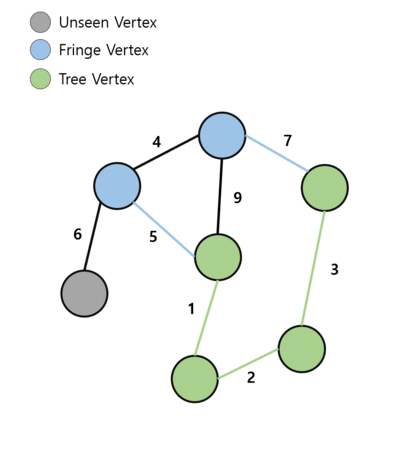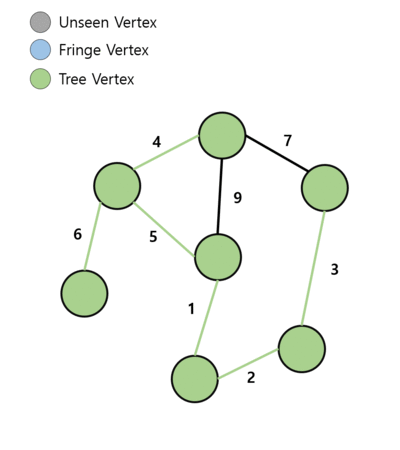
1. 시작 정점을 선택하여 Tree에 넣음
2. 트리에 들어간 정점에 연결된 간선을 찾음
2-1. 해당 간선으로 연결된 반대편 정점이 Unseen Vertex라면 해당 정점과 간선을 Fringe에 넣음
2-2. Fringe Vertex라면 가중치가 더 작은 간선으로 업데이트
3. Fringe의 정점들 중 간선의 가중치가 가장 작은 정점을 선택하여 트리에 넣음
4. 모든 정점이 트리에 포함될 때까지 2번 과정부터 반복
- Tree Vertex: 최소 신장 트리에 포함된 정점
- Fringe Vertex: 최소 신장 트리에 포함된 정점과 인접한 정점
- Unseen Vertex: Tree Vertex도, Fringe Vertex도 아닌 정점
분석
프림 알고리즘의 성능은 Fringe에서 가중치가 최소인 간선을 가지는 정점을 찾기 위해 사용하는 Priorty Queue를 어떻게 구현하냐에 따라 달라집니다. Priorty Queue를 Heap 으로 구현한 경우 프림 알고리즘은 O((V + E) · log V) 의 시간 복잡도를 갖습니다. Priorty Queue를 Unsorted Array 로 구현한 경우 프림 알고리즘은 O(v^2) 의 시간 복잡도를 갖습니다.
Kruskal's Algorithm
Kruskal's Algorithm이란?
크루스칼 알고리즘은 그래프에서 최소 신장 트리를 찾는 알고리즘으로 Greedy Algorithm 중 하나입니다. 크루스칼 알고리즘은 모든 정점을 각각 트리로 만들고 단계를 진행할 때마다 트리 합쳐 하나의 최소 신장 트리를 찾습니다. 크루스칼 알고리즘은 Union-Find 알고리즘을 이용하여 구현합니다.
Union-Find Algorithm
Disjoint Set을 표현하기 위한 알고리즘
Find는 각 원소가 어떤 집합에 속하는지 찾는 연산
Union은 두 원소가 속한 각 집합을 하나로 합치는 연산
과정
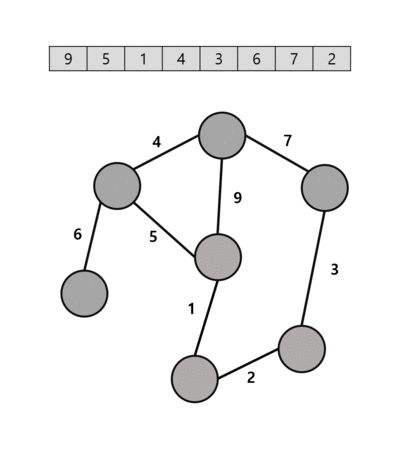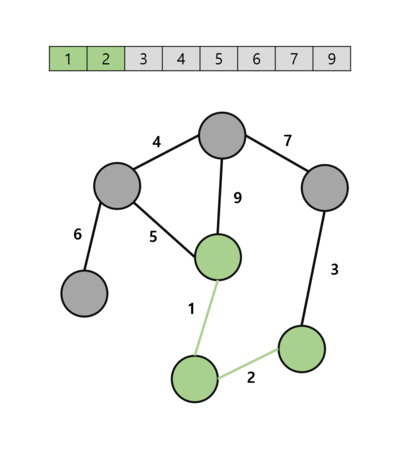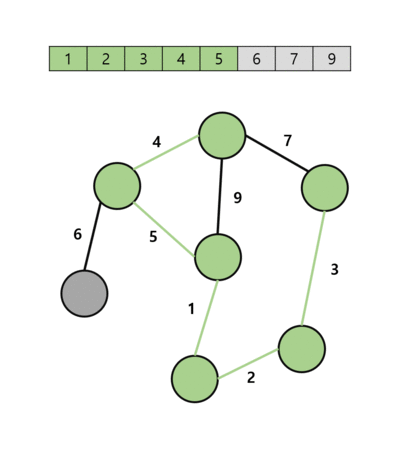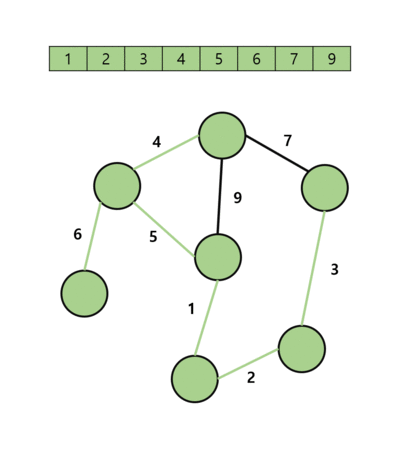
1. 가중치를 기준으로 간선 리스트를 정렬
2. 간선 리스트에서 가중치가 가장 작은 간선을 찾음
3. 해당 간선으로 연결된 두 정점을 찾음
4. Find 연산을 통해 두 정점이 다른 트리에 속해 있는지 확인
5. 다른 트리에 속해있다면 Union 연산을 통해 두 트리를 합침
6. 모든 정점이 하나의 트리에 속하게 될 때까지 2번 과정부터 반복
분석
크루스칼 알고리즘의 성능은 간선 리스트를 정렬하는 방법에 따라 좌우됩니다. 퀵 정렬과 같이 효율적인 알고리즘으로 정렬한다면 크루스칼 알고리즘은 O(E · log E) 의 시간 복잡도를 갖습니다.
