
관련 문제
2805번 - 나무 자르기
1654번 - 랜선 자르기
문제를 풀다 처음으로 이진 탐색으로 문제를 푸는 상황과 마주쳤다.
나무 자르기 문제를 풀었고, 해당 방법에 대해 아예 모르고 있던 것은 아니라 나름 이진 탐색으로 문제를 풀었고, 테스트 케이스에 대한 결과값도 잘 나왔다.
그러나 제출 결과 시간 초과가 발생했다.
아래는 문제의 그 코드이다.
n, m = map(int, input().split())
treeList = list(map(int, input().split()))
minLength = 1
maxLength = max(treeList)
while True:
if minLength+1 == maxLength:
search = maxLength
search = (maxLength + minLength) // 2
cutAble = (list(filter(lambda x: x-search > 0, treeList)))
cutTree = list(map(lambda x:x-search, cutAble))
sumCutLength = sum(cutTree)
if sumCutLength==m:
break
elif (sumCutLength < m):
maxLength = search
elif (sumCutLength > m):
minLength = search
print(search)본격적으로 문제를 풀기 위해서 이진 탐색에 대해 공부해본 경험은 없으므로 이진 탐색으로 어떻게 문제를 풀 수 있는지를 공부하고자 한다.
또한 같은 이진 탐색으로 문제를 풀더라도 어떤 것을 신경쓰며 문제를 풀어야할지 등에 대해 탐구 해보고자 한다.
이진 탐색 (Binary Search)
정렬된 리스트에서 검색 범위를 줄여 나가면서 검색 값을 찾는 알고리즘이다.
정렬된 리스트에만 사용할 수 있다는 단점이 있지만, 검색이 반복될 때마다 검색 범위가 절반으로 줄어 속도가 빠르다는 장점이 있다.
시간 복잡도는 O(logN)이다.
동작 방식
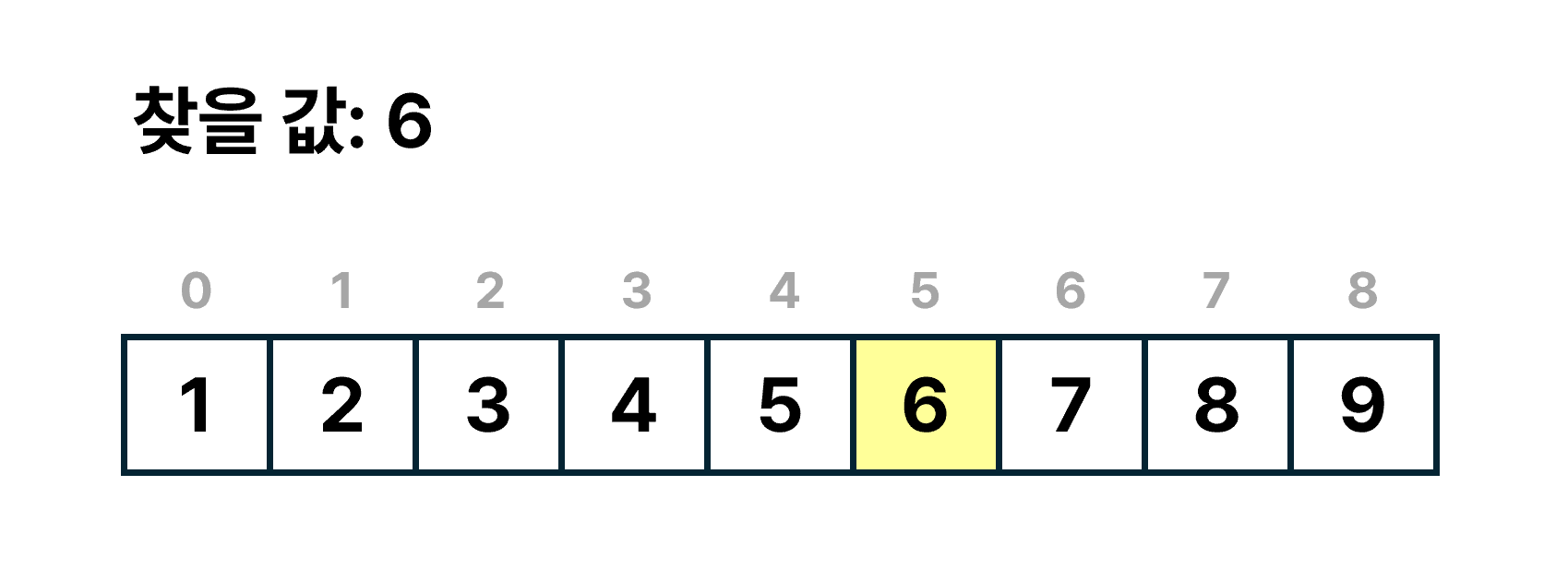
이진 탐색 알고리즘은 리스트의 중간값을 비교하여 검색값을 찾으므로, 위와같이 정렬된 배열에서만 사용할 수 있다.
편의상 해당 리스트를 list로 부르겠다.
list에서 6을 검색하는 상황을 가정해보자.
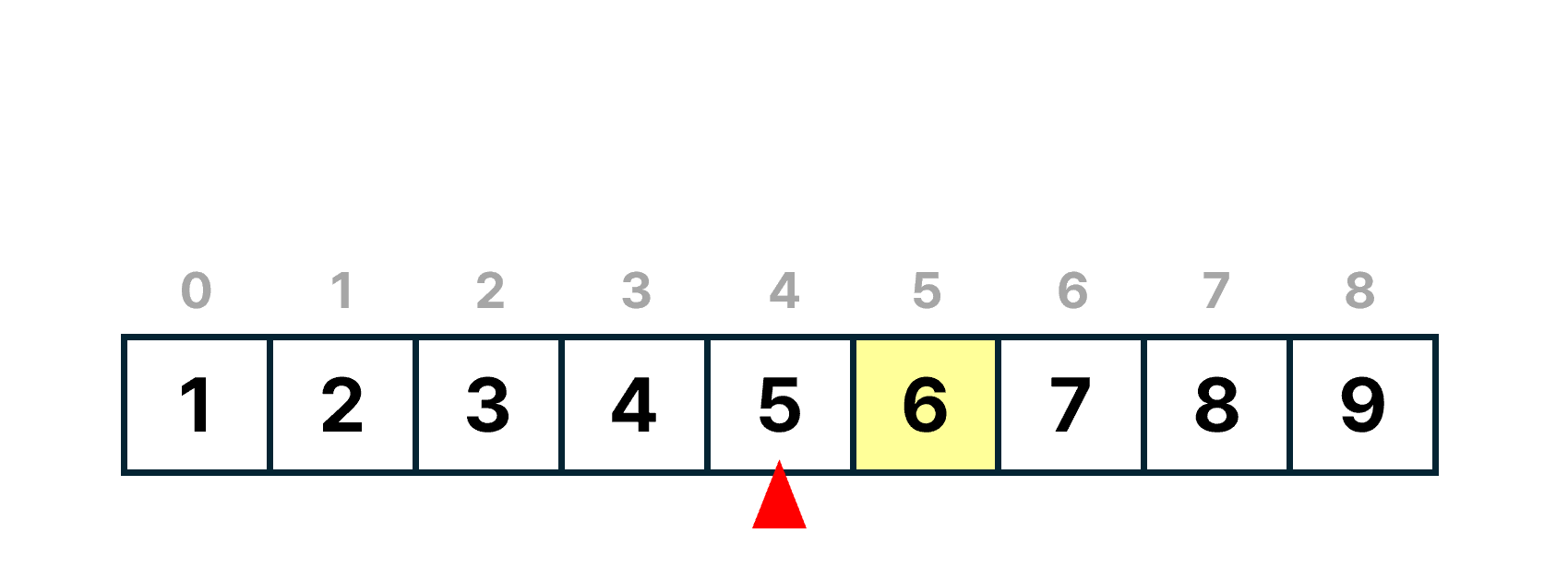
list의 인덱스는 0 ~ 8까지 존재한다.
따라서 0 ~ 8의 중간값을 구한다. ((0 + 8) // 2)
list[4]의 값을 찾을 값인 6과 비교한다.
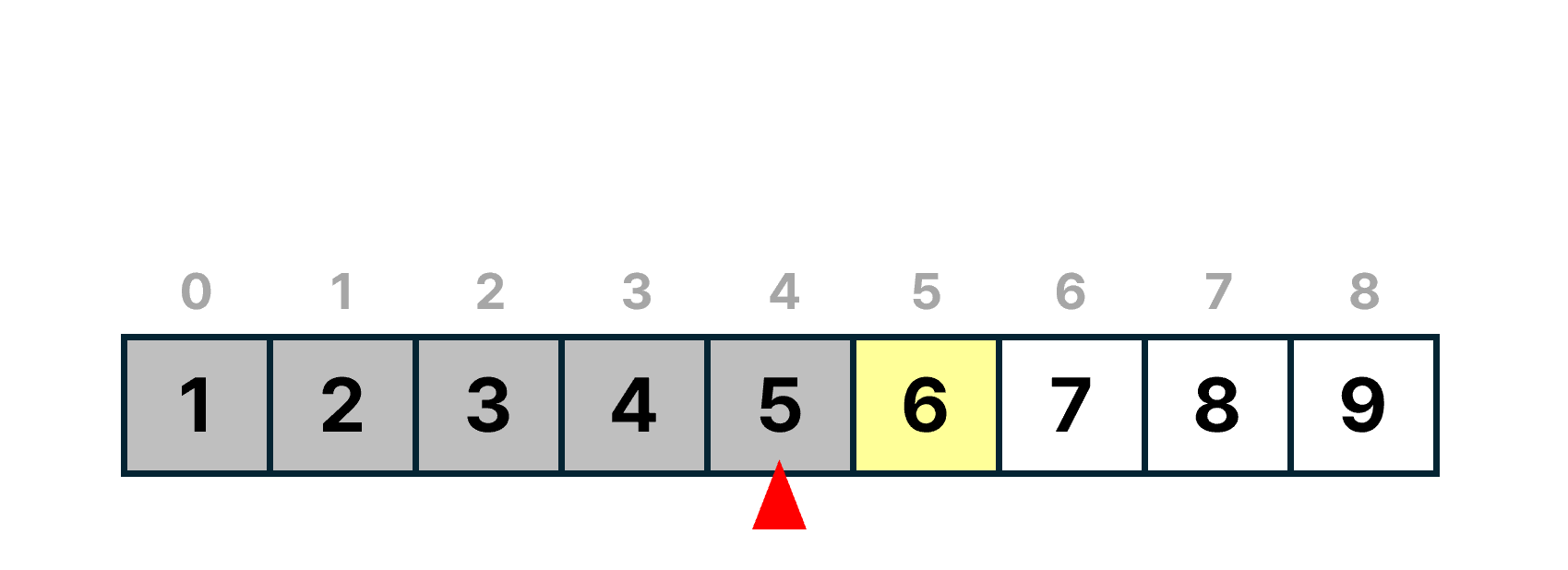
5는 6보다 작으므로, list[4]와 그 왼쪽에 위치하는 값들은 비교 대상에서 제외된다.
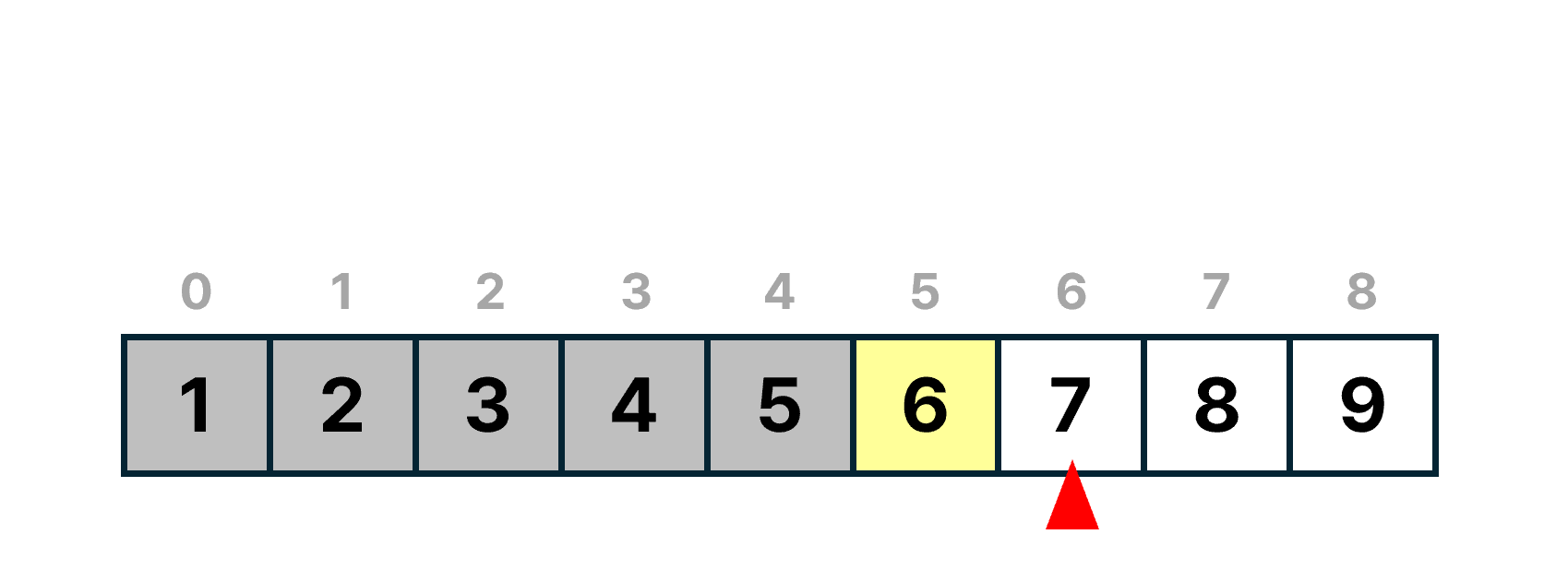
중간 값으로 선택되었던 인덱스의 다음 인덱스인 5번과 끝 값인 8번 인덱스의 중간값을 구한다. ((5 + 8) // 2)
list[6]의 값을 찾을 값 6과 비교한다.
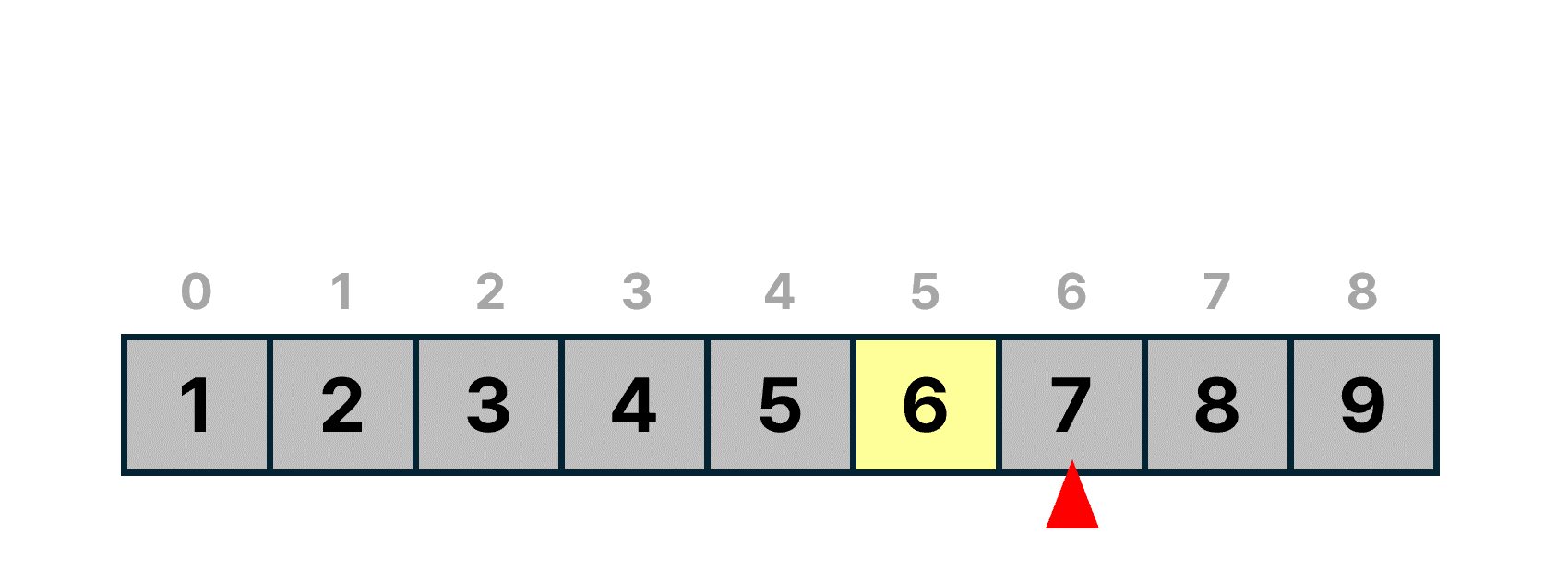
7은 6보다 크므로, list[6]과 그 오른쪽에 위치하는 값들은 비교 대상에서 제외된다.
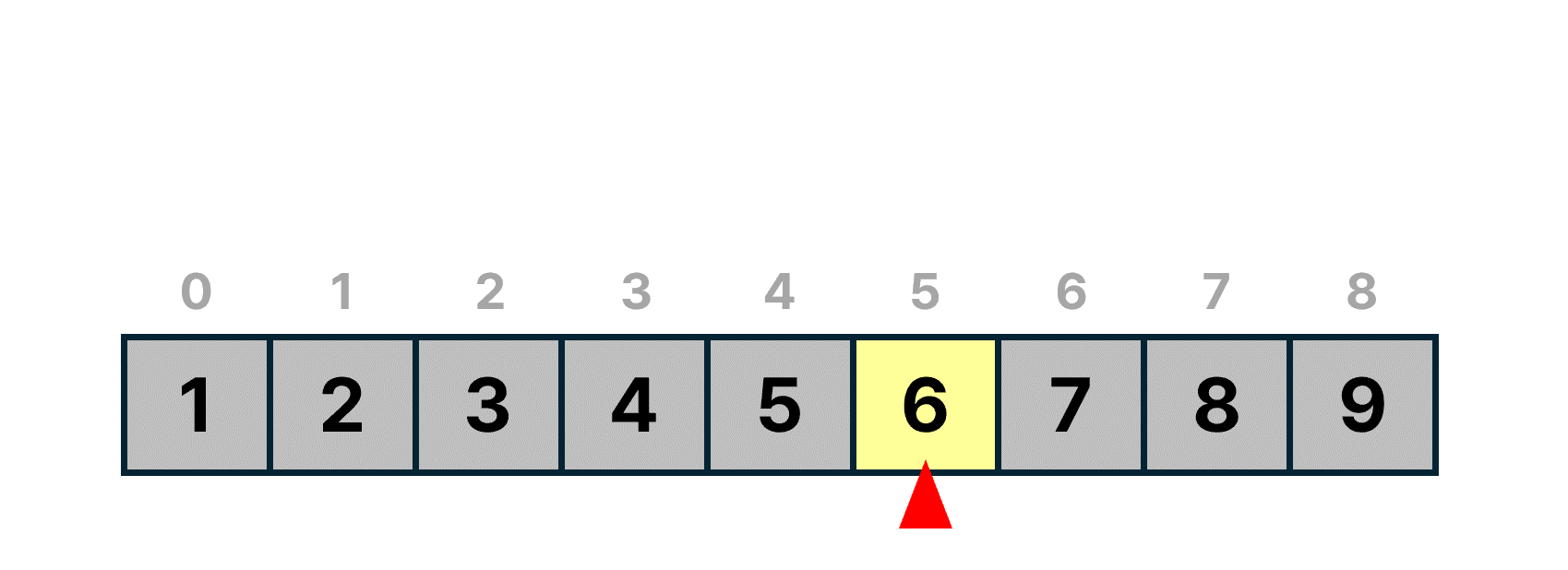
남은 배열의 중간값인 list[5]에 접근한다.
list[5]는 찾을 값인 6과 같다.
6을 찾았으므로 탐색을 종료한다.
이렇게 이진 탐색은 배열이 정렬돼 있다는 것을 활용하여 탐색할 범위를 매번 반으로 줄여나갈 수 있다.
종료 조건
- 검색을 성공할 경우
리스트에서 검색할 값과 같은 요소를 발견한 경우
if list[mid] = key: # 검색할 값을 찾는 경우 탐색을 종료, 해당 값 반환
break- 검색을 실패할 경우
더 이상 검색할 범위가 없을 경우
start > end 가 되는 경우
while start<=end: # start>end가 되는 경우 탐색을 종료한다.
...나무 자르기
n, m = map(int, input().split())
trees = list(map(int, input().split()))
start, end = 1, sum(trees)
# start와 end가 같아질 때까지 반복
while start <= end:
mid = (start + end) // 2 # 중간 위치
cnt = 0
# 나무 자르기
for tree in trees:
# 나무의 높이가 절단기 높이보다 크다면
if tree > mid:
# 자르기
cnt += tree - mid
# 자른 나무들의 길이가 목표값 이상이라면
if cnt >= m:
# 시작점 조정
start = mid + 1
# 목표값 이하라면
else:
# 끝점 조정
end = mid - 1
# 답 출력
print(end)맨 처음에 작성한 코드도 사실은 이진 탐색을 활용하고 있다.
그러나 처음 작성한 코드는 시간 초과 되었고, 위의 코드는 통과했다.
두 코드의 차이를 비교해보았다.
답은 연산의 횟수를 줄이는 것
두 코드는 연산의 횟수에 차이가 있었다.
내가 작성한 코드
입력받은 전체 나무 중 가장 긴 나무를 max로, 1을 min으로 저장한다.
1. min과 max의 중간값을 구한다.
2. 중간값으로 나무를 자를 수 있는지 판별한다.
3. 자를 수 있는 나무를 자르고 자른 나무 길이의 합을 구한다.
4. 나무 길이의 합을 m과 비교하여 min/max 값을 조정한다.
-> 1 ~ 4를 반복적으로 구한다.
다른 사람의 코드
입력받은 나무 전체 합을 end로, 1을 start로 저장한다.
1. start와 end의 중간값을 구한다.
2. 모든 나무에 대해 절단기 높이보다 나무의 높이가 크면 자르고 그 값을 더하는 연산을 수행한다.
3. 나무 길이의 합을 m과 비교하여 start/end 값을 조정한다.
-> 1 ~ 3을 반복적으로 구한다.
즉, 내가 작성한 코드는 자를 수 있는 나무를 판별하고, 그 합을 구하는 과정을 따로 분리하여 각각 연산해야 했던 것이다.
이런 과정 때문에 내 코드를 제출했을 때 시간 초과가 발생한 것으로 보인다.
연산 횟수를 더 줄이고 싶다면 3번 조건을 아래와 같이 수정하면 된다.
# 자른 나무들의 길이가 목표값과 같으면
if cnt == m:
end = mid
break
# 자른 나무들의 길이가 목표값 이상이라면
elif cnt > m:
# 시작점 조정
start = mid + 1
# 목표값 이하라면
else:
# 끝점 조정
end = mid - 1랜선 자르기
위의 방법을 참고하여 비슷한 유형인 랜선 자르기 문제를 풀어보았다.
import sys
k, n = map(int, input().split())
lineLength = [0] * k
for i in range(k):
lineLength[i] = int(sys.stdin.readline())
minLength = 1
maxLength = max(lineLength)
saveLength = [0, 0] # 자른 길이, 개수
if n==1:
print(lineLength[0])
sys.exit()
while minLength <= maxLength:
midLength = (minLength + maxLength) // 2
cnt = 0
for line in lineLength:
cnt += line // midLength
if cnt >= n:
minLength = midLength + 1
if saveLength[0] < midLength:
saveLength[0] = midLength
saveLength[1] = cnt
else:
maxLength = midLength - 1
print(saveLength[0])이 문제에서 주의할 점은 종료 조건을 잘 고려해주어야 한다.
나무 자르기 문제의 경우 m을 찾았을 경우 해당 값이 최댓값이기 때문에 탐색을 멈추고 값을 출력해도 됐다.
하지만 랜선 자르기 문제에서는 그렇게 하면 오답처리 된다.
해당 문제는 최대 랜선의 길이를 구해야 하는데, cnt==n을 찾더라도 자른 랜선의 길이가 최대 길이임을 보장하지 않기 때문이다.
랜선을 더 길게 자르는 다른 방법이 있을 수 있다.
느낀점
같은 이진 탐색 알고리즘이라고 하더라도 문제의 조건에 따라서 설정할 수 있는 종료 조건이 다를 수 있다는 것을 알게 되었다.
또한 앞으로 문제를 풀며 연산을 줄이는 방법에 대해서도 많이 고민을 해봐야겠다.
참고 자료
이진 탐색 (Binary search) 개념 및 구현
[백준 2805번] 나무 자르기 - 파이썬
[BOJ/백준] 2805번 나무 자르기 (매개변수 탐색) (Python 파이썬)
