문제링크: https://leetcode.com/problems/longest-increasing-subsequence/description/
1. 문제설명
1.1. 요구사항
주어진 정수 배열 nums에서 가장 긴 증가하는 부분 배열을 반환하라(주어진 정수의 순서를 위반하지 않는 것 같다).
1.2. 입출력 예시
Example 1:
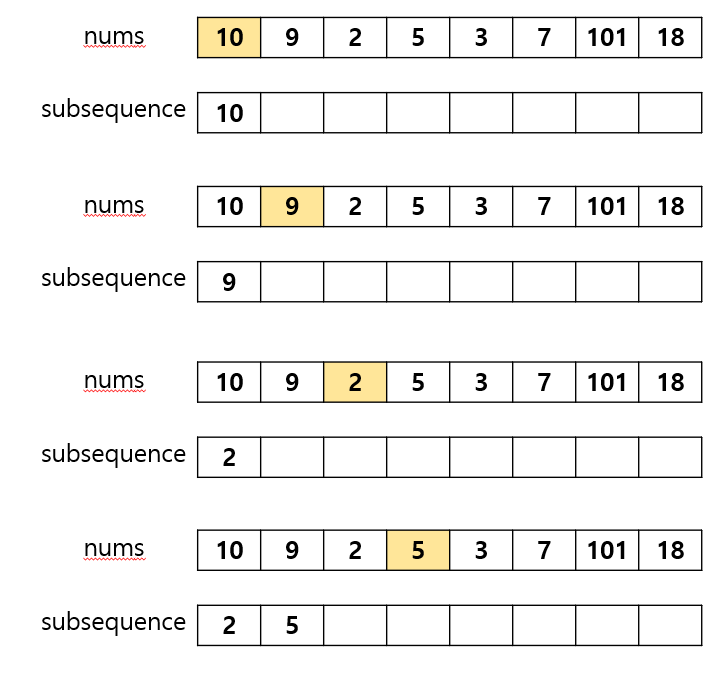
Input: nums = [10,9,2,5,3,7,101,18]
Output: 4
Explanation: The longest increasing subsequence is [2,3,7,101], therefore the length is 4.
Example 2:
Input: nums = [0,1,0,3,2,3]
Output: 4
Example 3:
Input: nums = [7,7,7,7,7,7,7]
Output: 1
1.3. 제한사항
- 1<= nums.length <= 2500
- -10^4 <= nums[i] <= 10^4
2. 풀이
2.1. 나의 생각
브루트포스를 활용하여 원소들을 추출 할 생각까지 미쳤지만 성능이 너무 저하되고 문제에서 요구하는 O(n log(n))시간을 맟출 수 없으므로 고민 끝에 타인의 풀이에 도움을 받았다.
이번 문제에서 중요한 부분은 주어진 배열에서 subsequence배열을 생성하여 가장 긴 배열의 상태를 유지하는 것에 있었다.
그를 위해 필요한 것이 nums와 같은 길이의 부분배열 저장공간과 저장공간에 유지중인 가장 긴 배열의 길이를 저장소가 필요했다. 이를 각각 subsequence와 maxSize라고 명명했다.
그리고 nums를 순회하면서 아래와 같은 원칙으로 정수를 부분배열에 추가한다.
- nums[i]가 부분배열의 모든 요소보다 크다면 nums[i]를 추가하고 maxSize의 크기를 1 증가시킨다.
- nums[i]가 가장 크지 않다면 자신보다 작은 원소중 가장 큰 원소의 뒤 자리에 정보를 저장한다.
위와 같은 원칙을 따르면 가장 긴 배열의 정보 자체를 완벽하게 유지 할 수는 없지만 가장 긴 길이 maxSize를 알아낼 수 있었다.
subsequence에 정수를 추가할 때는 배열이 오름차순을 유지하기 때문에 이진탐색을 사용하여 요소를 추가할 수 있으므로 log n의 시간이 들어가고 nums배열을 순회하는 시간 n까지 해서 전체 시간복잡도가 O(nlog(n))인 것을 알 수 있다.